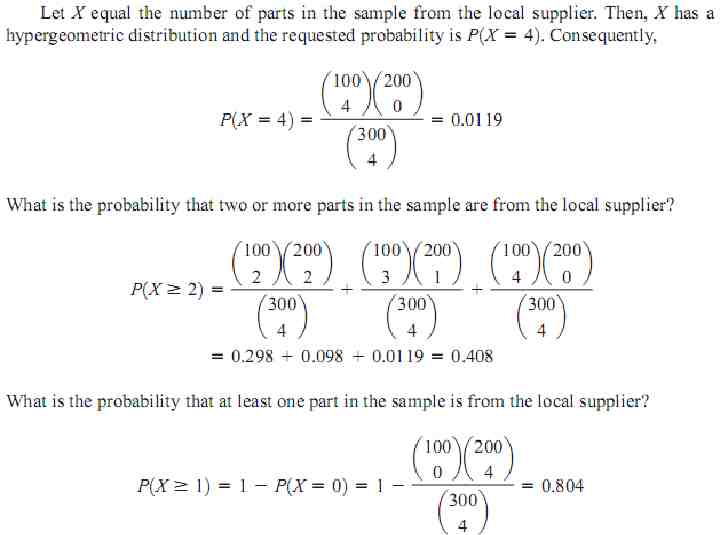Why this can be happen to me?

Why this can be happen to me?

Can you think, who’ll be the faster catch the fish?

Chapter 3 Special Distribution

What’s distribution we learn for?

An Applied Example about Distribution ; discrete/ continue Premium industry value in insurance

DISCRETE UNIFORM DISTRIBUTION Example : The first digit of a part’s serial number is equally likely to be any one of the digits 0 through 9. If one part is selected from a large batch and X is the first digit of the serial number, X has a discrete uniform distribution with probability 0.1 for each value. R {0,1, 9} f(x) 0.1 for each value in R

Mean & Variance discrete UNIFORM Prove it (H1)

Example Let the random variable Y denote the proportion of the 48 voice lines that are in use at a particular time. Assume that X is a discrete uniform random variable with a range of 0 to 48. then E(X) (48 0)/2 24 2 48 0 1 1 / 12 1/ 2 14.14

Bernoulli & Binomial Distribution A trial with only two possible outcome Bernoulli Trial Assumed that the trial that constitute the random experiment are independent This implies that the outcome from one trial has no effect on the outcome to be obtained from any other trial It often reasonable to assume that the probability of a success in each trial is constant

A rV X, if an experiment can result only in “success” (E) or failure (E’) then the corresponding Bernoulli rV is : 1, if e E X (e) 0, if e E ' The pdf of X is given by f(0) q, f(1) p. Pdf of Bernoulli distribution can be expressed as : x 1 x f ( x) p q , x 0,1

Mean and Variance Prove it

Ex Rolls of a four sided die. A bet occur on a single roll of the die. Thus E {1} p 1/4 E’ {2,3,4} is placed that a 1 will

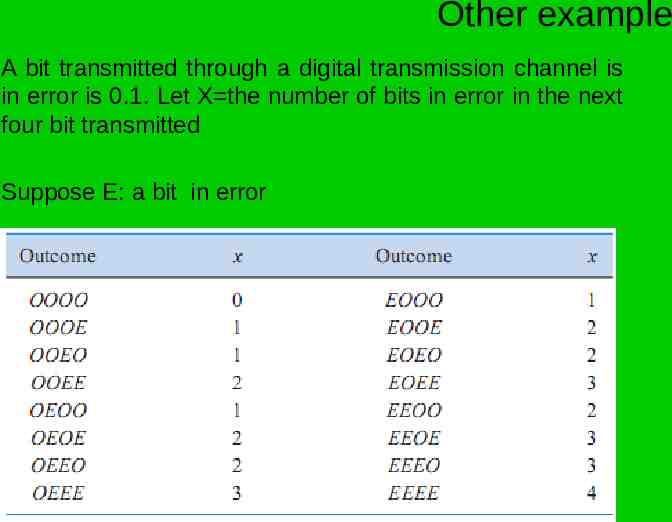
Other example A bit transmitted through a digital transmission channel is in error is 0.1. Let X the number of bits in error in the next four bit transmitted Suppose E: a bit in error

The event that X 2 consists of the 6 outcome : {EEOO, EOEO, EOOE, OEEO, OEOE, OOEE} Using the assumption that the trials are independent that the probability of the {EEOO} is : 2 2 P EEOO P( E ) P( E ) P(O) P(O) 0.1 0.9 0.0081 in general, P X x number of outcomes that result in x error) times ( 0.1 )x( 0.9 )4 x

Bernoulli Distr

Example Each sample of water has a 10% chance of containing a particular organic pollutant. Assume the samples are independent with regard to the presence of the pollutant. Find the probability that in the next 18 samples, exactly 2 contain the pollutant. Let X the number of samples that contain the pollutant in the next 18 samples analyzed. Then X is a binomial rV with p 0.1 and n 18 Therefore : 18 2 16 P X 2 0.1 0.9 2

Geometric Distribution Is a distribution arising from Bernoulli trials is the number of trials to the first occurrence of success Ex: The probability that a bit transmitted through a digital transmission channel is received in error is 0.1. Assume the transmissions are independent event and let the rV X denote the number of bits transmitted until the first error

answer P(X 5) is the probability that the first four bits are transmitted correctly and the fifth bits is in error Denoted : {OOOOE} where O denotes an okay bit Because the trial are independent and the probability of a correct transmission is 0.9 then P X 5 P OOOOE 0.9 4 0.1 0.066

Definition Prove it (H2)

Negative Binomial distribution Suppose previously example. Let the RV X denote the number of bits transmitted until the fourth error Then find P(X 10)

X has a negative binomial distribution with r 4 P(X 10) is the probability that exactly three errors occur in the first nine trials and then trial 10 result in the fourth error The probability that exactly three errors occur in the first nine trial is determined from the binomial distribution to be 9 0.1 3 0.9 6 3 Because the trial are independent, probability that exactly three errors occur in the first 9 trials and trial 10 results in the fourth error is the product of the probabilities of these two events, namely : 9 9 3 6 0.1 0.9 0.1 0.1 4 0.9 6 3 3

definition Prove it (H3)

Hypergeometric Distribution Prove it (H4)

Example A batch of parts contains 100 parts from a local supplier of tubing and 200 parts from a supplier of tubing in the next state. If four parts are selected randomly and without replacement, what is the probability they are all from the local supplier?

Poisson Distribution Ex: passenger arrivals at an airline terminal The distribution of dust particles

Consider the transmission of n bits over a digital communication channel. Let the rV X equal the number of bit error. When the probability that a bit is in error is constant and the transmissions are independent, X has a binomial distribution. Let p denote the probability that a bit is in error. Let pn, E ( x) pn n x P X x p (1 p) n x x x n 1 x n n n x Suppose n increase and p decrease accordingly such that : E X , e x P X x , x 0,1,2,. lim x! n

definition