Using Logic Criterion Feasibility to Reduce Test Set Size While

Using Logic Criterion Feasibility to Reduce Test Set Size While Guaranteeing Double Fault Detection Gary Kaminski and Paul Ammann Software Engineering Group George Mason University Presented at Mutation 2009 April 4, 2009 Denver, Colorado

Return of the HOMs Higher Order Mutants (HOMs) – Applying multiple mutant operators: if (x y) { a b c;} if (x b) { a b * c;} – Banished as unnecessary (Offutt) – Single Order Mutants (SOMs) are enough They’re Baaaaaaack! – Tests that kill HOMS can be really powerful! A HOM may be better than relevant SOMs –Jia/Harmon, Polo et al This paper looks at test sets adequate to detect a 2

Motivation Consider coverage as a way to – Generate mutation adequate tests – Statically! In this paper, we consider double HOMS – Generate “small” test sets Smaller than “MUMCUT ” – But still guarantee double HOM detection Restrictions in this paper: – Only worry about mutating predicates – Assume minimal Disjunctive Normal Form (DNF) – Assume predicates are tested in isolation 3

Minimal DNF Terms separated by OR, literals by AND ab a!c vs. a(b !c) Make each term true and other terms false ab ac vs. ab abc Can’t remove a literal without changing predicate’s truth value ab vs. abc ab!c Green – in minimal DNF Red – not in minimal DNF 4

Minimal DNF: SOMs and HOMs Original Predicate: ab bc Literal Insertion Fault (LIF): Literal Reference Fault (LRF): Literal Omission Fault (LOF): abc bc ac bc a bc Detecting LIF, LRF, LOF actually detects all 9 SOM types The LIF and LRF can result in an equivalent fault HOM: Double Fault: abc ba 81 double faults HOMs What can we say about detecting double fault HOMs? 5

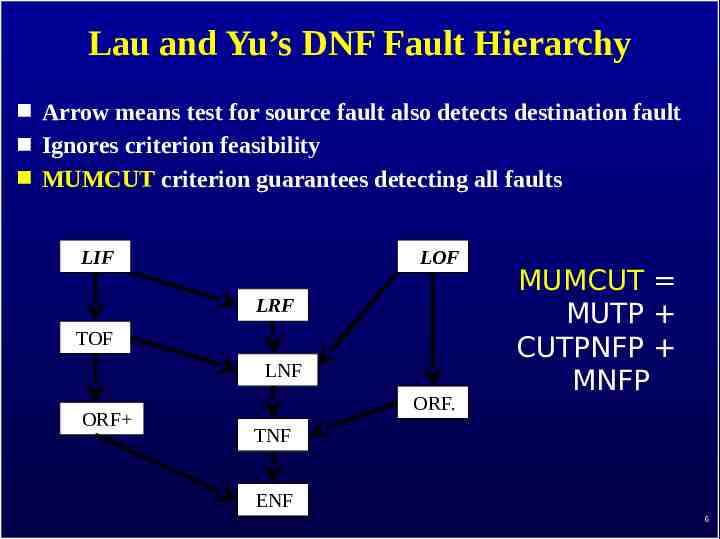
Lau and Yu’s DNF Fault Hierarchy Arrow means test for source fault also detects destination fault Ignores criterion feasibility MUMCUT criterion guarantees detecting all faults LIF LOF LRF TOF LNF ORF ORF. MUMCUT MUTP CUTPNFP MNFP TNF ENF 6

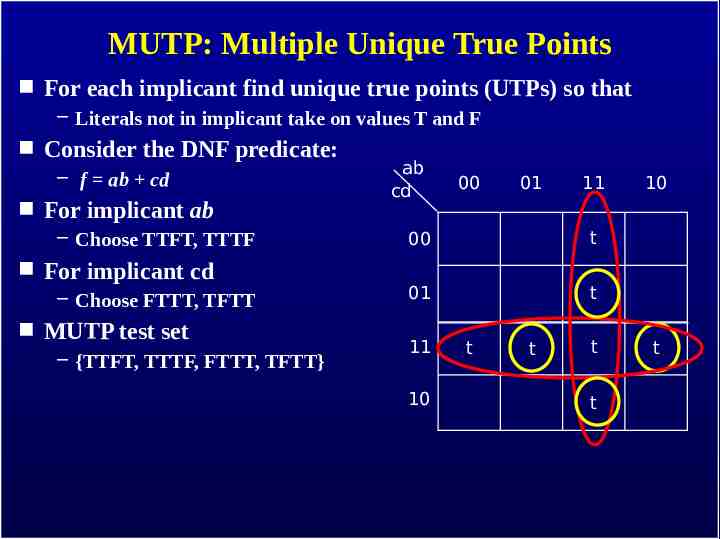
MUTP: Multiple Unique True Points For each implicant find unique true points (UTPs) so that – Literals not in implicant take on values T and F Consider the DNF predicate: – f ab cd For implicant ab – Choose TTFT, TTTF For implicant cd – Choose FTTT, TFTT MUTP test set – {TTFT, TTTF, FTTT, TFTT} ab cd 00 01 11 00 t 01 t 11 10 t t t t 10 t

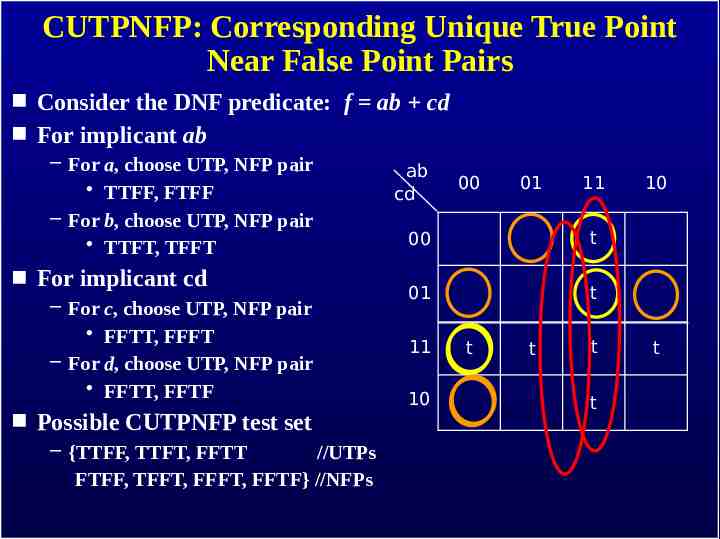
CUTPNFP: Corresponding Unique True Point Near False Point Pairs Consider the DNF predicate: f ab cd For implicant ab – For a, choose UTP, NFP pair TTFF, FTFF – For b, choose UTP, NFP pair TTFT, TFFT For implicant cd – For c, choose UTP, NFP pair FFTT, FFFT – For d, choose UTP, NFP pair FFTT, FFTF Possible CUTPNFP test set – {TTFF, TTFT, FFTT //UTPs FTFF, TFFT, FFFT, FFTF} //NFPs ab cd 00 01 11 00 t 01 t 11 10 t t t t 10 t

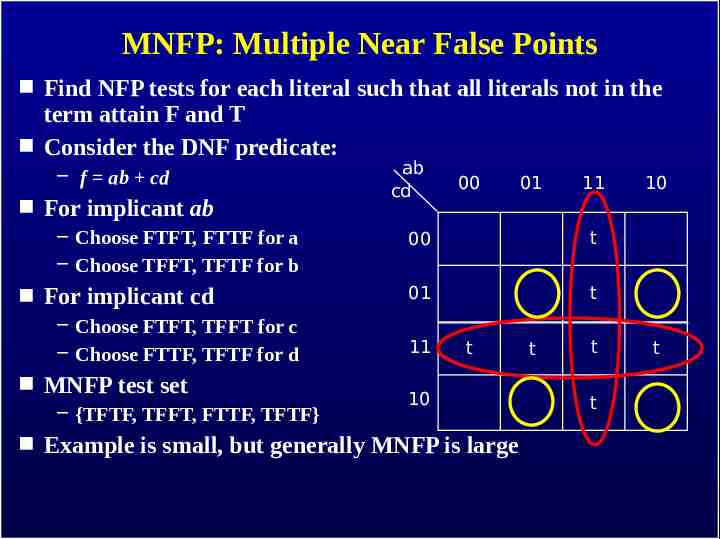
MNFP: Multiple Near False Points Find NFP tests for each literal such that all literals not in the term attain F and T Consider the DNF predicate: – f ab cd For implicant ab – Choose FTFT, FTTF for a – Choose TFFT, TFTF for b For implicant cd – Choose FTFT, TFFT for c – Choose FTTF, TFTF for d MNFP test set – {TFTF, TFFT, FTTF, TFTF} ab cd 00 01 11 00 t 01 t 11 t 10 Example is small, but generally MNFP is large t t t 10 t

Minimal-MUMCUT Criterion Kaminski/Ammann (ICST 2009) Minimal-MUMCUT uses low level criterion feasibility analysis – Adds CUTPNFP and MNFP only when necessary Minimal-MUMCUT guarantees detecting LIF, LRF, LOF – And thus all 9 faults in the hierarchy For Each Term MUTP feasible? For Each Literal In Term CUTPNF P MNFP Test Set MUTP MNFP feasible? Test Set MUTP NFP Test Set MUTP CUTPNFP 10

First Result: What About the Double Faults? MUMCUT vs. Minimal-MUMCUT – Exactly the same detection for double faults – Detect 75 of 81 possible double fault types Both MUMCUT and Minimal-MUMCUT – May miss 6 of 81 possible double fault types 11

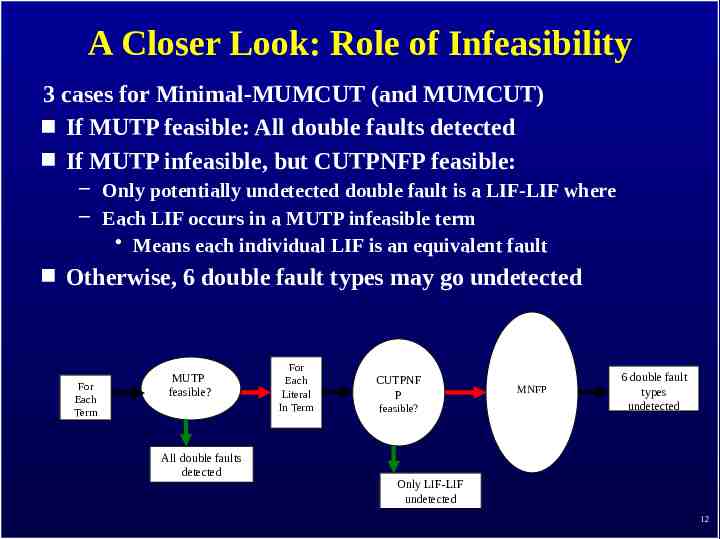
A Closer Look: Role of Infeasibility 3 cases for Minimal-MUMCUT (and MUMCUT) If MUTP feasible: All double faults detected If MUTP infeasible, but CUTPNFP feasible: – Only potentially undetected double fault is a LIF-LIF where – Each LIF occurs in a MUTP infeasible term Means each individual LIF is an equivalent fault Otherwise, 6 double fault types may go undetected For Each Term MUTP feasible? All double faults detected For Each Literal In Term CUTPNF P feasible? MNFP 6 double fault types undetected Only LIF-LIF undetected 12

Question: How to Handle 6 Undetected Double Faults? Coverage criteria approach: – Develop suitable criteria and apply in all cases (Lau et al) – Example: SMOTP: Supplementary Multiple Overlapping True Points Detects LIF-LIF double fault, but is very expensive – Similar strategy for other 5 undetected double faults Alternate approach: – Look at actual artifacts under test See if there is a problem If so, handle it; Otherwise, forget about it Reviewer comment: What does this have to do with Mutation? – I think this alternate approach is the key 13

A Look at Some Artifacts Analyzed 19 TCAS predicates with 5 to 13 unique literals (Weyuker, Chen, Lau, Yu) Built a tool in Java to: Determine MUTP feasibility for each term and CUTPNFP feasibility for each literal Generate a Minimal-MUMCUT test set Analysis: – Which double fault types go undetected? – What percentage of double faults go undetected? 14

Case Study Results 99.9% of non-equivalent double faults are detected because: 1) 23% of terms were MUTP feasible (all double faults detected) 2) 100% of the literals were CUTPNFP feasible - Only 1 of the 6 double fault types (LIF-LIF) went undetected 3) 98.5% of double faults formed by two equivalent LIFs are equivalent Equivalent a!bd a!cd e a!bd!e a!cd!e e Not Equivalent (TFFTF) a!bd a!cd e a!bdc a!cdb e 15

Detecting the LIF-LIF Supplement Minimal-MUMCUT with Overlapping True Points (OTPs) for terms only when MUTP is infeasible for both terms OTPs make two terms true Original: a!bd a!cd e MUTP not feasible for a!bd or a!cd OTP for a!bd and a!cd is TFFTF ab cd 00 01 11 10 t t 00 01 11 t 10 TFFTF detects the following LIF-LIF: a!bdc a!cdb e Result: Test set augmented with select OTPs detects 76 of 81 faults (modulo certain feasibility assumptions) 16

Internal Variable Problem What input values satisfy a criterion? – Predicates are deep in the code – Must reach predicate and have variables in predicate attain certain truth values – Partial solutions using constraints exist What if you can’t solve internal variable problem? – Potentially need to redo the analysis – If a Minimal-MUMCUT test is infeasible Need to replace it with tests farther down the hierarchy This work is in progress 17

Minimal DNF in Practice 1) 95% of 20,256 Boolean predicates in avionics software were in minimal DNF* 2) MUMCUT has been shown to detect 99% of corresponding faults in non-minimal DNF Boolean predicates* *Source: Y.T Yu and M.F. Lau. Comparing Several Coverage Criteria for Detecting Faults in Logical Decisions. In Proceedings QSIC 2004: 4th International Conference on Quality Software, Pages 14-21. 18

How Many Literals? Minimal-MUMCUT for software with predicates having at least 4 unique literals Exhaustive coverage for 4 unique literals - ab !ac - 6 Minimal-MUMCUT tests vs. 8 exhaustive tests Avionics software often has predicates with many unique literals* *Source: J.J Chilenski and S.P. Miller. Applicability of modified condition/decision coverage to software testing. IEE/BCS Software Engineering Journal, 9(5): 193-200, September 1994. 19

Conclusion Introduction of Minimal-MUMCUT which guarantees the same double fault detection as MUMCUT with smaller test set size Analysis of relationship between criterion feasibility and double fault detection Examination of what double faults are likely undetected in practice by Minimal-MUMCUT and how to extend Minimal-MUMCUT accordingly Applications for software testing of programs with large predicates 20

Logic Criteria How should inputs be chosen to test software? One answer: to achieve logic coverage Logic criteria impose requirements on inputs if (a b) Make expression evaluate to T and F (TF,FF) Make each literal evaluate to T and F (FT,TF) Provide a stopping rule for testing Guarantee logic faults are detected 21

Unique True Points and Near False Points UTP: An assignment of values such that only one term evaluates to true. ab !ac: 110 and 111 are UTPs for ab NFP: An assignment of values such that the predicate evaluates to false but when a literal is omitted, it evaluates to true. ab !ac: 100 and 101 are NFPs for b 22

MUTP Criterion (Chen, Lau, Yu) Find UTP tests for each term such that all literals not in the term attain F and T. Detects LIF and if feasible, detects LRF Inexpensive to satisfy Feasible for term ab in ab !ac ab – TTF, TTT Infeasible for term ab in ab ac ab – TTF 23

CUTPNFP Criterion (Chen, Lau, Yu) Find a UTP - NFP pair such that only the literal of interest changes value. Detects LOF and if feasible, detects LRF More expensive to satisfy Feasible for b in first term of ab ac UTP for ab is TTF NFP for b in ab is TFF Infeasible for b in first term of ab b!c !bc UTP for ab is TTT NFP for b in ab is TFF (TFT makes tern !bc true) 24

MNFP Criterion (Chen, Lau, Yu) Find NFP tests for each literal such that all literals not in the term attain F and T. Detects LOF and if feasible, detects LRF Most expensive to satisfy Feasible for a in first term of ab ac FTF, FTT Infeasible for a in first term of ab !ac FTF (FTT makes term !ac true) 25

MUMCUT Criterion (Chen, Lau, Yu) Combines MUTP, CUTPNFP, and MNFP – Guarantees detection of all faults in the hierarchy – Fairly expensive criterion 26

Second Result: Dealing with 6 Undetected Double Faults One approach: – Develop criteria to detect these faults, and apply in all cases (Lau et al) – Example SMOTP: Supplementary Multiple Overlapping True Points Detects LIF-LIF double fault But is very expensive – Similar strategy for other 5 undetected double faults Alternate approach: – Analyze predicates to see which double faults might evade detection – Only add additional tests if needed – Illustrate this approach via a case study 27