UNIT – 3 DOMAIN TESTING Domain: domain is a set of possible values

UNIT – 3 DOMAIN TESTING Domain: domain is a set of possible values of an independent variable or the variables of a function Domain testing attempts to determine whether the classification is or is not correct Fig 3.1

BUG ASSUMPTION: Domain Errors: 1.Double Zero Representation 2.Floating point zero check 3.Contradictory domains 4. Ambiguous domains 5.Over specified Domains 6.Boundary Errors 7.Closure Reversal 8.Faulty Logic

RESTRICTIONS TO DOMAIN TESTING : 1.Co-incidental Correctness :Domain testing isn't good at finding bugs for which the outcome is correct for the wrong reasons 2. Representative Outcome : Domain testing is an example of partition testing. Partition-testing strategies divide the program's input space into domains such that all inputs within a domain are equivalent 3.Simple Domain Boundaries and Compound Predicates

For example, x 0 AND x 17, just specifies two domain boundaries by one compound predicate 4.Functional Homogeneity of Bugs : Whatever the bug is, it will not change the functional form of the boundary predicate 5.Linear Vector Space 6.Loop Free Software : Loops are problematic for domain testing. The trouble with loops is that each iteration can result in a different predicate expression

NICE DOMAINS: 1.Domains are and will be defined by an imperfect iterative process aimed at achieving (user, buyer, voter) satisfaction 2.Implemented domains can't be incomplete or inconsistent. Every input will be processed, possibly forever. Inconsistent domains will be : made consistent. 3. Conversely, specified domains can be incomplete and/or inconsistent.

Incomplete in this context means that there are input vectors for which no path is specified and inconsistent means that there are at least two contradictory specifications over the same segment of the input space Some important properties of nice domains are: Linear, Complete, Systematic, And : Orthogonal, Consistently closed, Convex and simply connected

. Fig3.2: Nice Two-Dimensional Domains 1.LINEAR AND NON LINEAR BOUNDARIES Nice domain boundaries are defined by linear inequalities or equations E.G ax b 0 The impact on testing stems from the fact that it takes only two points to determine a straight line and three points to determine a plane and in general n 1 point to determine a n-dimensional hyper plane

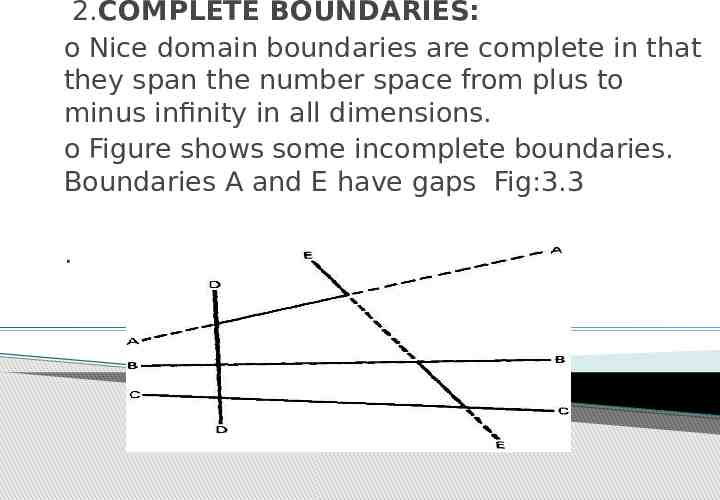
2.COMPLETE BOUNDARIES: o Nice domain boundaries are complete in that they span the number space from plus to minus infinity in all dimensions. o Figure shows some incomplete boundaries. Boundaries A and E have gaps Fig:3.3 .

3.SYSTEMATIC BOUNDARIES: Systematic boundary means that boundary inequalities related by a simple function such as a constant. : where fi is an arbitrary linear function, X is the input vector, ki and c are constants, and g(i,c) is a decent function over i and c that yields a constant, such as k ic.

4.ORTHOGONAL BOUNDARIES: i)Two boundary sets U and V (See Figure 3.2) are said to be orthogonal if every inequality in V is perpendicular to every inequality in U ii)If two boundary sets are orthogonal, then they can be tested independently 5.CLOSURE CONSISTENCY: : i) Figure 4.6 shows another desirable domain property: boundary closures are consistent and systematic.

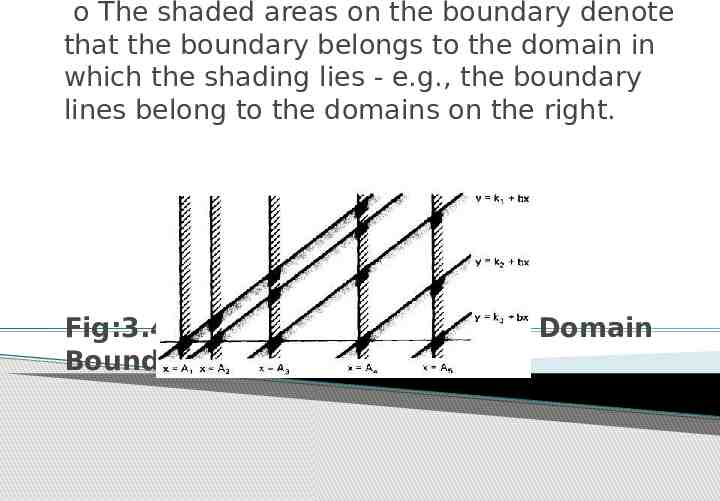
o The shaded areas on the boundary denote that the boundary belongs to the domain in which the shading lies - e.g., the boundary lines belong to the domains on the right. : Fig:3.4 Linear, Non-orthogonal Domain Boundaries

6.CONVEX: o A geometric figure (in any number of dimensions) is convex if you can take two arbitrary points on any two different boundaries, join them by a line and all points on that line lie within the figure. 7.SIMPLY CONNECTED: o Nice domains are simply connected; that is, they are in one piece rather than pieces all over the place intersperse ( mix together or spread or combine) with other domains.

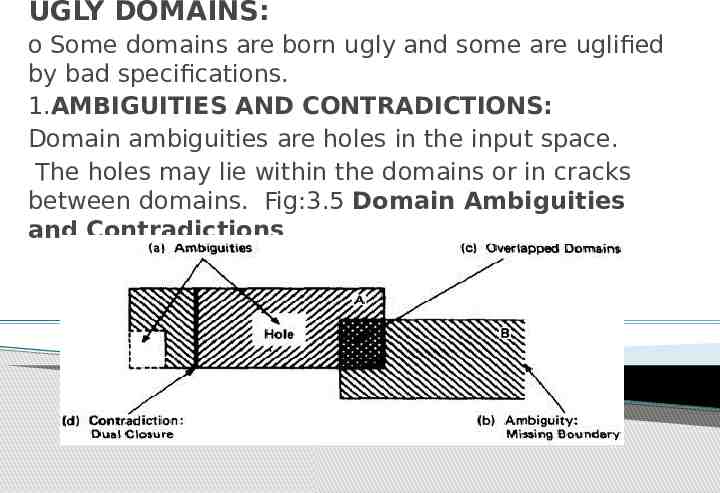
UGLY DOMAINS: o Some domains are born ugly and some are uglified by bad specifications. 1.AMBIGUITIES AND CONTRADICTIONS: Domain ambiguities are holes in the input space. The holes may lie within the domains or in cracks between domains. Fig:3.5 Domain Ambiguities and Contradictions

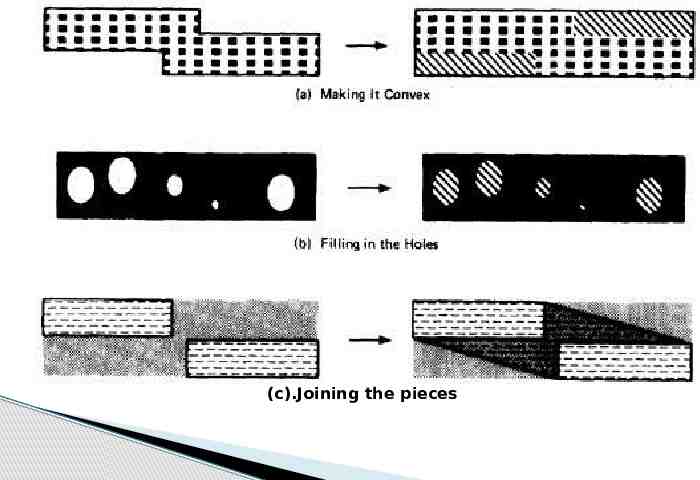
SIMPLIFYING THE TOPOLOGY: o The programmer's and tester's reaction to complex domains is the same - simplify o There are three generic cases: concavities, holes and disconnected pieces. o Programmers introduce bugs and testers misdesign test cases by: smoothing out concavities (Figure 3.6a), filling in holes (Figure 3.6b), and joining disconnected pieces (Figure 3.6c).

(c).Joining the pieces

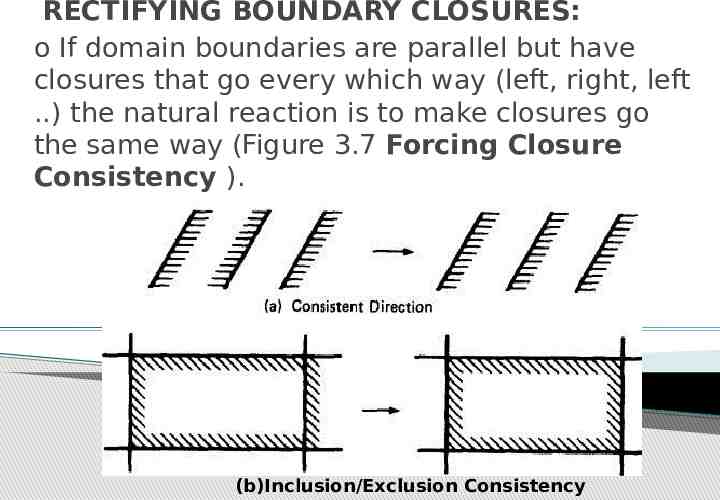
RECTIFYING BOUNDARY CLOSURES: o If domain boundaries are parallel but have closures that go every which way (left, right, left .) the natural reaction is to make closures go the same way (Figure 3.7 Forcing Closure Consistency ). (b)Inclusion/Exclusion Consistency

DOMAIN TESTING STRATEGY : 1. Domains are defined by their boundaries; therefore, domain testing concentrates test points on or near boundaries. 2.Pick enough points to test for all recognized kinds of boundary errors. 3. Because every boundary serves at least two different domains, test points used to check one domain can also be used to check adjacent domains.

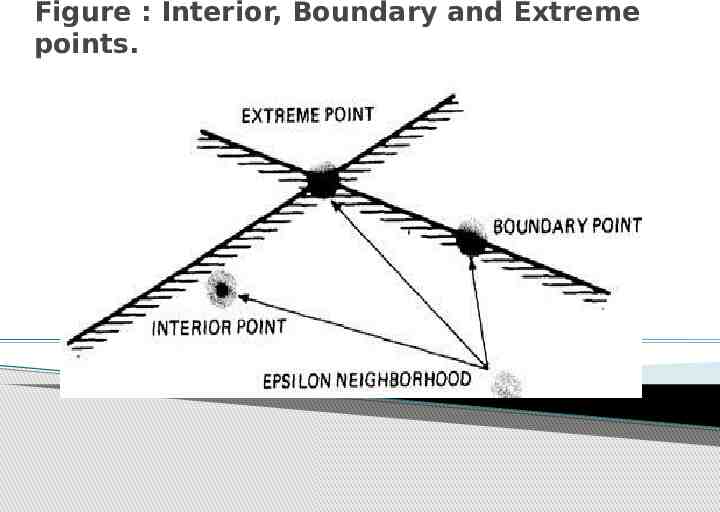
DOMAIN BUGS AND HOW TO TEST FOR THEM: o An interior point (Figure ) is a point in the domain such that all points within an arbitrarily small distance (called an epsilon neighborhood) are also in the domain. o A boundary point is one such that within an epsilon neighborhood there are points both in the domain and not in the domain. o An extreme point is a point that does not lie between any two other arbitrary but distinct points of a (convex) domain.

Figure : Interior, Boundary and Extreme points.

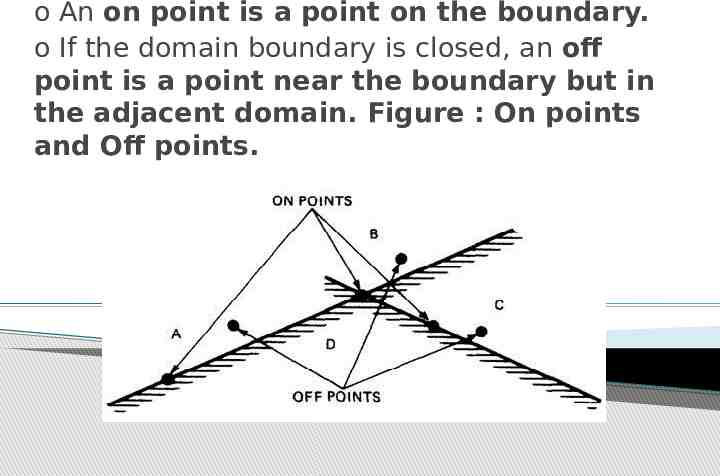
o An on point is a point on the boundary. o If the domain boundary is closed, an off point is a point near the boundary but in the adjacent domain. Figure : On points and Off points.

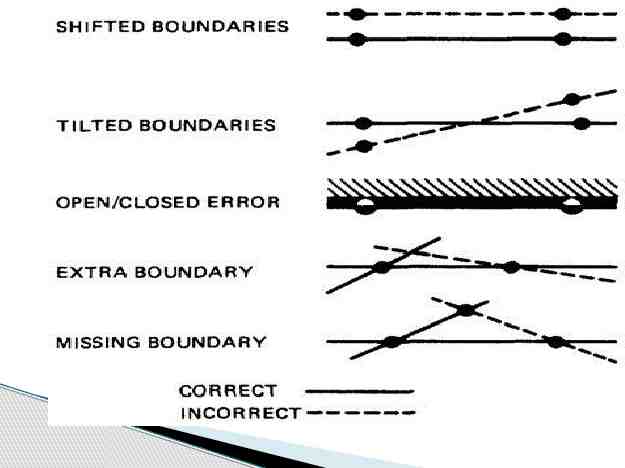
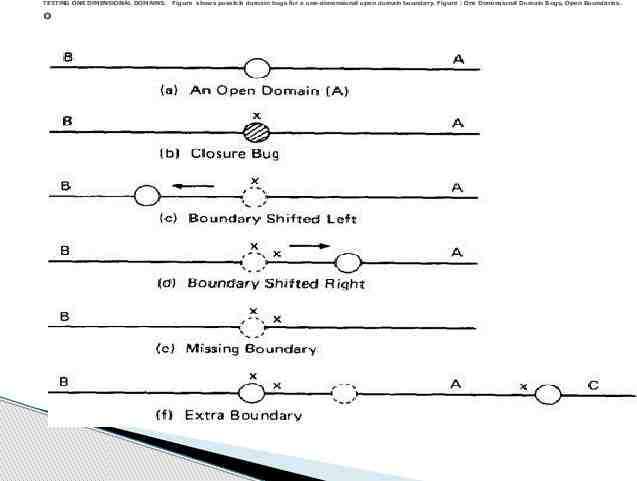
TESTING ONE DIMENSIONAL DOMAINS: o Figure shows possible domain bugs for a one-dimensional open domain boundary. Figure : One Dimensional Domain Bugs, Open Boundaries.

TESTING ONE DIMENSIONAL DOMAINS: o Figure shows possible domain bugs for a one-dimensional closed domain boundary. Figure : One Dimensional Domain Bugs, Closed Boundaries.

TESTING TWO DIMENSIONAL DOMAINS: o Figure 4.15 shows possible domain boundary bugs for a two-dimensional domain. o A and B are adjacent domains and the boundary is closed with respect to A, which means that it is open with respect to B.