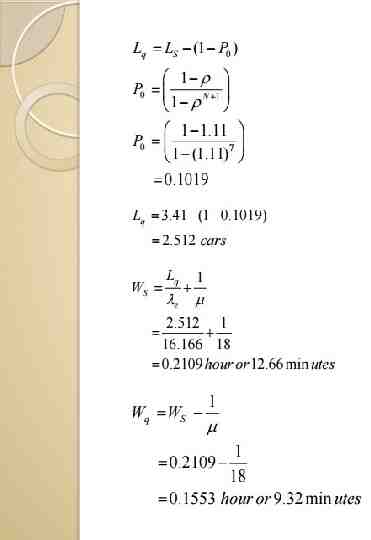Topic IV. Single Channel Systems (Limited queue length system)

Topic IV. Single Channel Systems (Limited queue length system) Olga Marukhina, Associate Professor, Control System Optimization Department, Tomsk Polytechnic University [email protected]

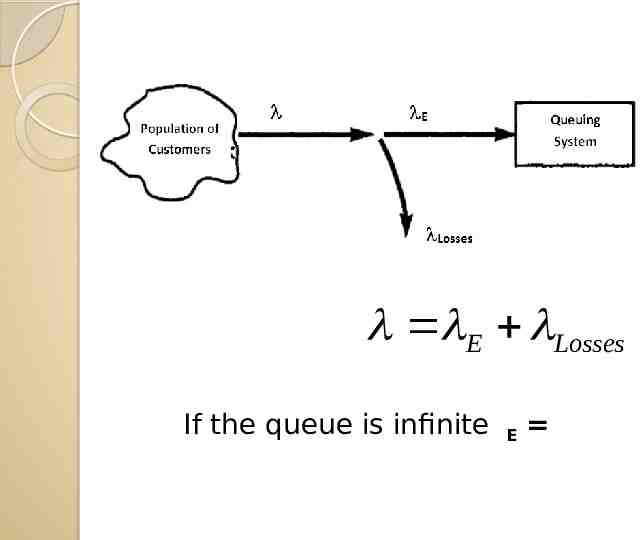
In real cases, queues never become infinite, but are limited due to space, time or service operating policy. Such queuing model falls under the category of finite queues. Finite queue models restrict the number of customers allowed in service system. That means if N represents the maximum number of customers allowed in the service system, then the (N 1)th arrival will depart without being part of the service system. Next client did not get into the system Only three chairs for waiting A hairdresser

Model B (M/M/1): ( /N/ ) Single-Channel Queuing Model with Poisson Arrivals and Exponential Service Times with a finite queue The service system can accommodate N customers only. The (N 1)th customer will not join the queue. Due to restriction in the allowable number of customers in the system, the service system will be interested to know the expected number of customers who are lost. This can be found out by determining the probability of customers not joining the system.

E Losses If the queue is infinite E

Example I The arrival rate of cars at GRAND jewelers is 20 cars per hour. The service rate at jeweler shop is 18 cars per hour. The only parking area at GRAND jewelers is restricted to 6 cars only. The arrival rate and service rate follows Poisson distribution. Identify the type of queue and then determine the performance measures of this queue. Utilization factor can be more then 1 for this type of system! Why? l 20 cars per hour; µ 18 cars per hour; N 6 cars. 20 1.11 18

For you! Automobiles arrive at the drive-through window at the downtown Urbana, Illinois, post office at the rate of 4 every 10 minutes. The average service time is 5 minutes. The only parking area at near windows is restricted to 5 cars only. The Poisson distribution is appropriate for the arrival rate and service times are exponentially distributed. a) What is the E ? b) What is the average time a car is in the system? b) What is the average number of cars in the system? c) What is the average number of cars waiting to receive service? d) What is the average time a car is in the queue? e) What is probability that there are no cars at the window? f) What percentage of the time is the postal clerk busy? g) What is the probability that there are exactly 2 cars in the system?

Thank you for attention!