Today Lecture 21: Quantum Information Science and the role

Today Lecture 21: Quantum Information Science and the role of Superconductivity Discussion of applications of superconductor materials and devices in five parts: 1. Overview of the quantum information landscape 2. Macroscopic quantum phenomena in superconductor devices and superconductor qubits 3. Transmon qubit --- the leading qubit platform 4. Topological superconducting qubits based on Majorana fermion states 5. S-TI-S Josephson junctions --- a compelling platform Next time Lecture 21: Macroscopic quantum phenomena and superconductor qubits

PHYS 498 SQD Fall 2019 Superconductor Materials and Devices for Quantum Information Science Relevance to Quantum Information Science: There is probably no area hotter in science than quantum information Recent discoveries and progress have made people worldwide aware of the potential of quantum mechanics for advanced detectors and quantum computing There are significant investments by countries, industries, and universities (including ours) in this area: UIUC has launched IQUIST Illinois Quantum Information Science and Technology Center, and created CQE Chicago Quantum Exchange, a consortium of partners in and near Chicago, to promote activity in QIS, including encouraging training of students in QIS via courses like this So, this NOT a course on QIS and I actually do NOT consider myself to be an expert in this emerging field But superconductivity is one of the leading and most promising hardware approaches for achieving the goals of this effort and it is to likely play a major role in qubit devices and quantum circuits, so I want to learn with you about what is happening and how to advance it Throughout the course we will keep an eye on new developments and opportunities for superconductivity

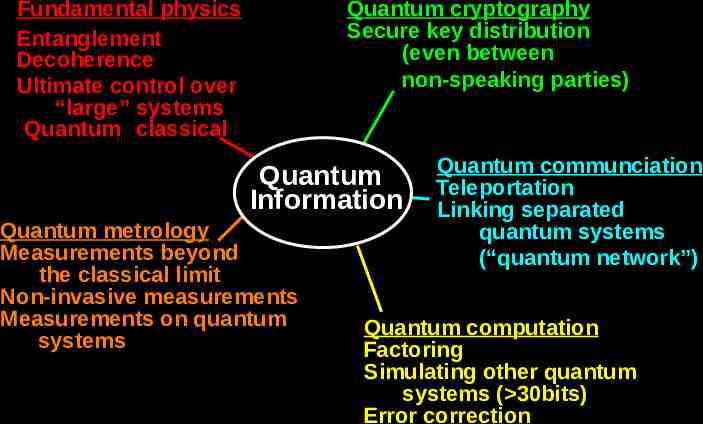
Quantum cryptography Secure key distribution (even between non-speaking parties) Fundamental physics Entanglement Decoherence Ultimate control over “large” systems Quantum classical Quantum Information Quantum metrology Measurements beyond the classical limit Non-invasive measurements Measurements on quantum systems Quantum communciation Teleportation Linking separated quantum systems (“quantum network”) Quantum computation Factoring Simulating other quantum systems ( 30bits) Error correction

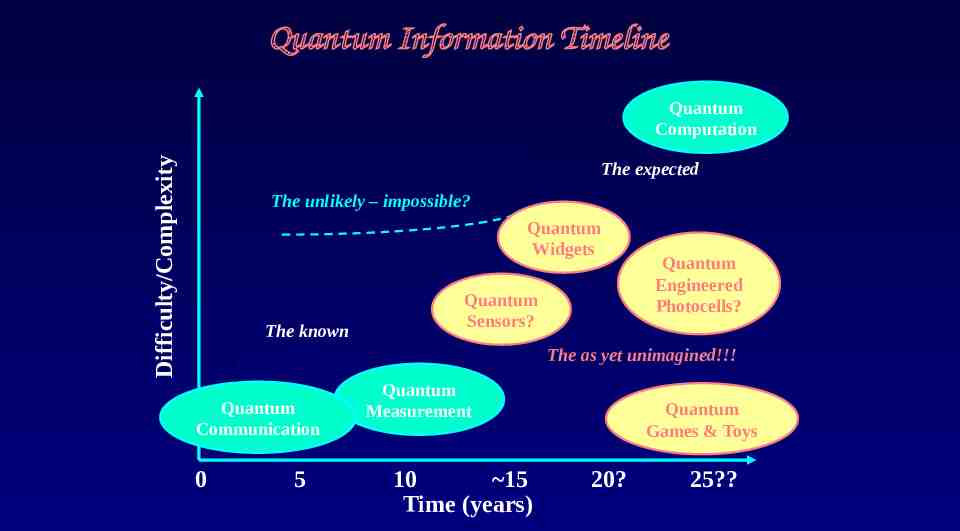
Quantum Information Timeline Difficulty/Complexity Quantum Computation The expected The unlikely – impossible? Quantum Widgets The known Quantum Sensors? Quantum Engineered Photocells? The as yet unimagined!!! Quantum Communication 0 5 Quantum Measurement 10 15 Time (years) Quantum Games & Toys 20? 25?

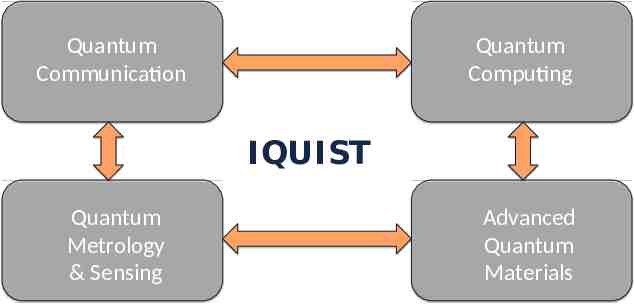
Quantum Communica on Quantum Compu ng IQUIST Quantum Metrology & Sensing Advanced Quantum Materials

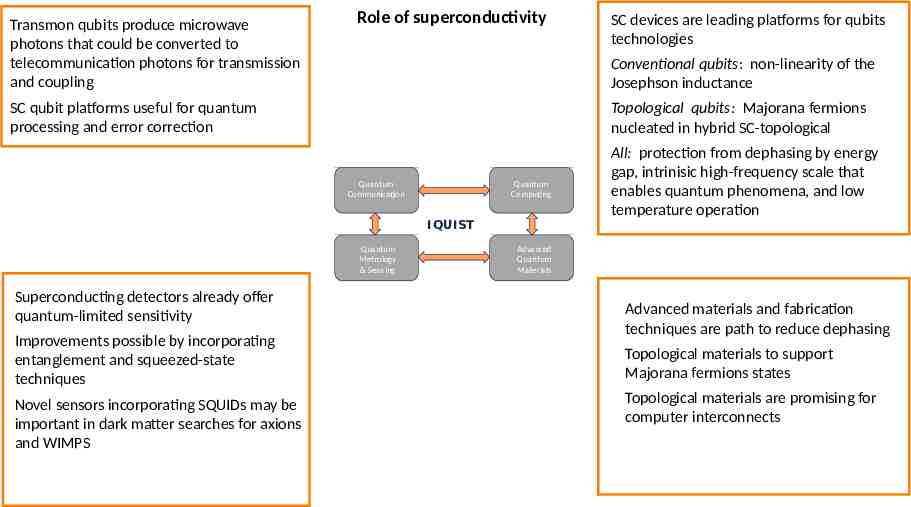
Transmon qubits produce microwave photons that could be converted to telecommunication photons for transmission and coupling Role of superconductivity Conventional qubits: non-linearity of the Josephson inductance SC qubit platforms useful for quantum processing and error correction Topological qubits: Majorana fermions nucleated in hybrid SC-topological Quantum Communica on Quantum Compu ng IQUIST Quantum Metrology & Sensing Superconducting detectors already offer quantum-limited sensitivity Improvements possible by incorporating entanglement and squeezed-state techniques Novel sensors incorporating SQUIDs may be important in dark matter searches for axions and WIMPS SC devices are leading platforms for qubits technologies All: protection from dephasing by energy gap, intrinisic high-frequency scale that enables quantum phenomena, and low temperature operation Advanced Quantum Materials Advanced materials and fabrication techniques are path to reduce dephasing Topological materials to support Majorana fermions states Topological materials are promising for computer interconnects

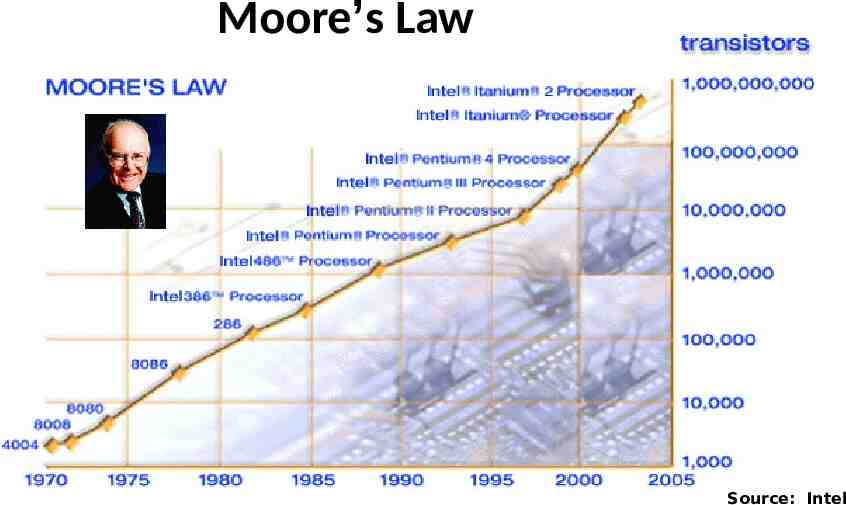
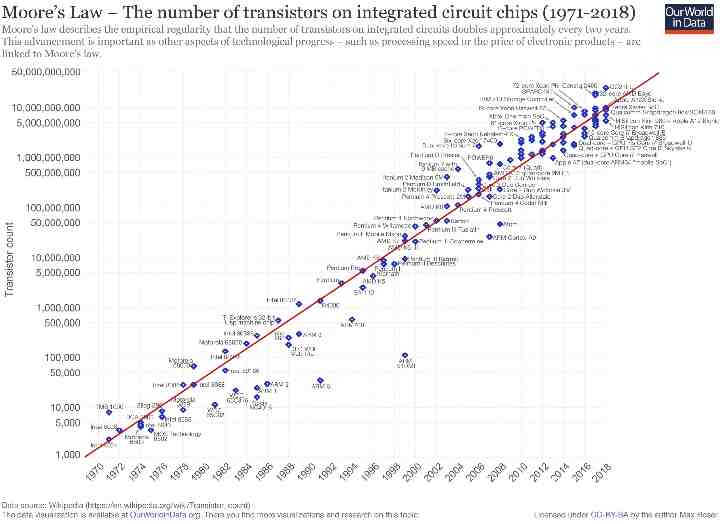
Primary drivers for Quantum information Science 1. Quantum computing ---- beyond Moore’s Law 2. Secure data communications --- encryption codes 3. Exciting science enabled by quantum computing

https://www.factbasedinsight.com/quantum-outlook-2019/

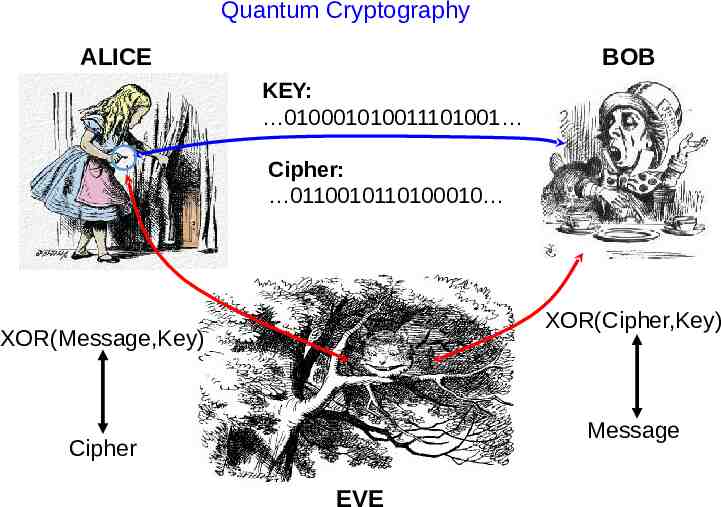
Quantum Cryptography ALICE BOB KEY: 010001010011101001 Cipher: 0110010110100010 XOR(Cipher,Key) XOR(Message,Key) Message Cipher EVE

Moore’s Law Source: Intel

The first solid-state transistor (Bardeen, Brattain & Shockley, 1947)

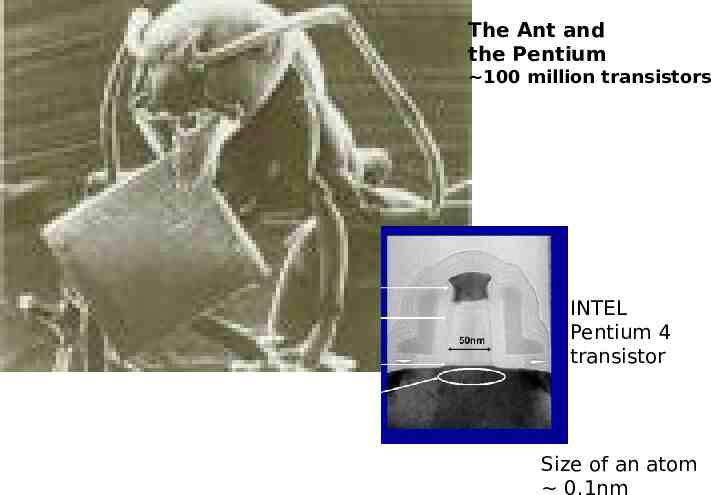
The Ant and the Pentium 100 million transistors INTEL Pentium 4 transistor Size of an atom 0.1nm

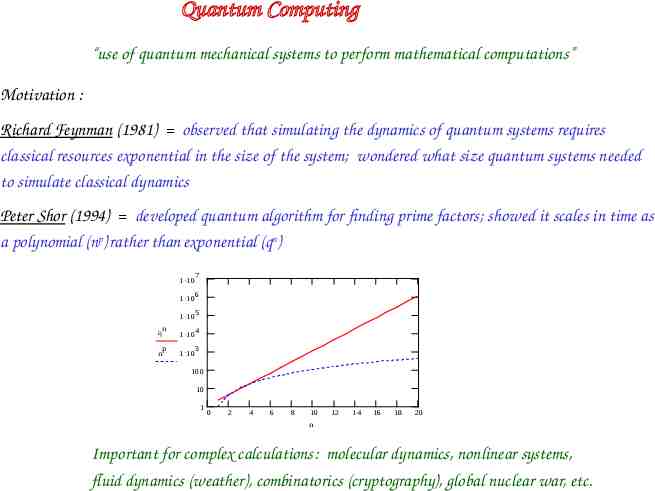
Quantum Computing “use of quantum mechanical systems to perform mathematical computations” Motivation : Richard Feynman (1981) observed that simulating the dynamics of quantum systems requires classical resources exponential in the size of the system; wondered what size quantum systems needed to simulate classical dynamics Peter Shor (1994) developed quantum algorithm for finding prime factors; showed it scales in time as a polynomial (np) rather than exponential (qn) 7 1 10 6 1 10 5 1 10 n q 4 1 10 p n 3 1 10 100 10 1 0 2 4 6 8 10 12 14 16 18 20 n Important for complex calculations: molecular dynamics, nonlinear systems, fluid dynamics (weather), combinatorics (cryptography), global nuclear war, etc.

Shor's algorithm is a quantum computer algorithm for integer factorization. Informally, it solves the following problem: Given an integer N, find its prime factors. It was invented in 1994 by the American mathematician Peter Shor. On a quantum computer, to factor an integer N, Shor's algorithm runs in polynomial time (the time taken is polynomial in log N, the size of the integer given as input). Specifically, it takes quantum gates of order ((log N)²(log log N)(log log log N)) using fast multiplication, thus demonstrating that the integer-factorization problem can be efficiently solved on a quantum computer and is consequently in the complexity class BQP. A hard problem: factoring large integers: For example, it is hard to factor 167,659 But an elementary school student can easily multiply 389 x 431 167,659 This asymmetry in the difficulty of factoring vs. multiplying is the basis of public key encryption, on which everything from on-line transaction security to ensuring diplomatic secrecy depends.

Lov Grover (1996) algorithm for “exhaustive search” identify an item having a specific property out of N items classical algorithm requires N/2 steps to succeed 50% of the time quantum algorithm requires only N1/2 steps useful for many computations Example: Data Encryption Standard 256 bit code 7 x 1016 possible keys classical computer 1000 years @106 keys per second quantum computer 4 minutes !

Quantum Supremacy In quantum computing, quantum supremacy is the goal of demonstrating that a programmable quantum device can solve a problem that classical computers practically cannot (irrespective of the usefulness of the problem).[1][2] By comparison, the weaker quantum advantage is the demonstration that a quantum device can solve a problem merely faster than classical computers. Conceptually, this goal involves both the engineering task of building a powerful quantum computer and the computational-complexity-theoretic task of finding a problem that can be solved with current technology and has a believed superpolynomial speedup over the best known or possible classical algorithm for that task.[3][4] The term was originally popularized by John Preskill[1] but the concept of a quantum computational advantage, specifically for simulating quantum systems, dates back to Yuri Manin's (1980)[5] and Richard Feynman's (1981) proposals of quantum computing.[6]

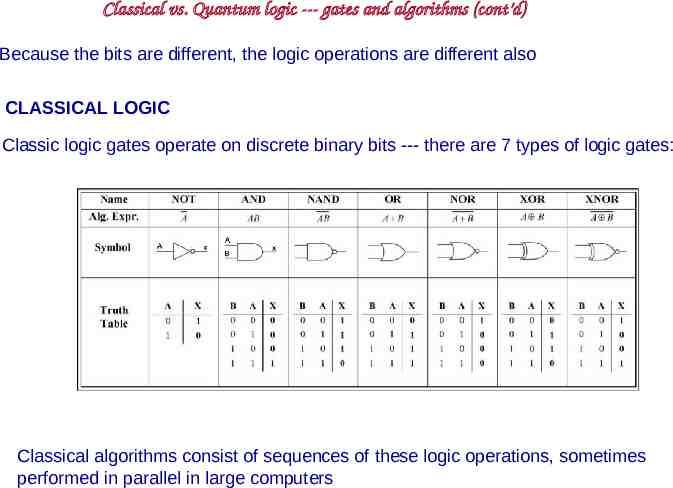
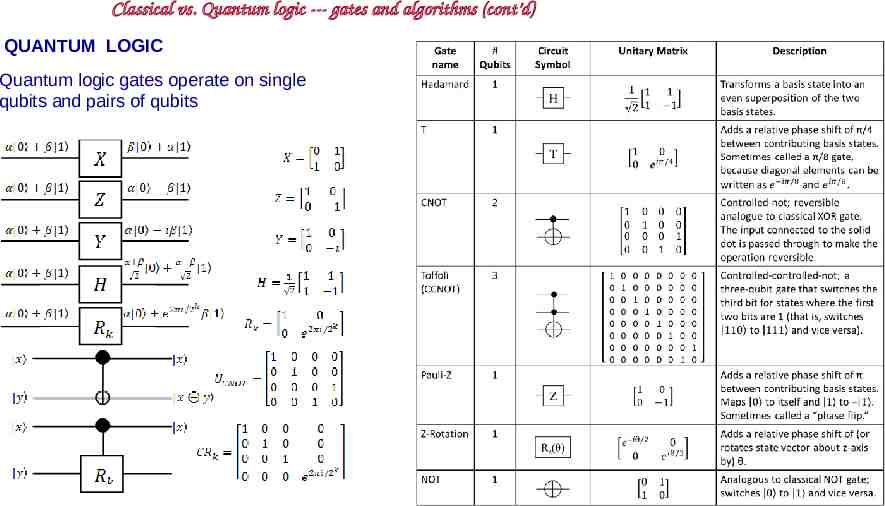
Classic vs. Quantum Logic CLASSICAL LOGIC: two distinct states “bit” 0 or 1 can do all operations from NOT and exclusive-OR gates Single-bit operation Two-bit operation perform series of operations on bits to get final answer QUANTUM LOGIC: superposition of two quantum levels “qubit” quantum bit a 0 b 1 can do all operations from single-qubit and controlled-NOT functions unitary transformations (e.g. rotations) Two-qubit operation “Entangle” qubits and allow quantum evolution to “project out” answer

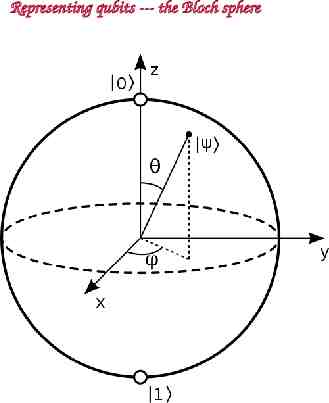
Representing qubits --- the Bloch sphere

Key to quantum computation entanglement qubit quantum two-level system 0 and 1 1 Superposition: a 0 b 1 0 E1 E0 0 Entanglement: interference of two qubits 1 q A 00 B 01 C 10 D 11 Performing logic operations with entangled states allows the quantum evolution to sample multiple states effectively massive parallel computation Quantum mechanically, a register of N entangled qubits can store 2N states in superposition: e.g. A 300-qubit register can simultaneously store 2300 1090 numbers 2037035976334486086268445688409378161051468393665936250636140449354381299763336706183397376 This is more than the total number of particles in the Universe! (Google SC quantum computer has 57 qubits only 144,115,188,075,855,872 states) Some problems benefit from this exponential scaling, enabling solutions of otherwise insoluble problems.

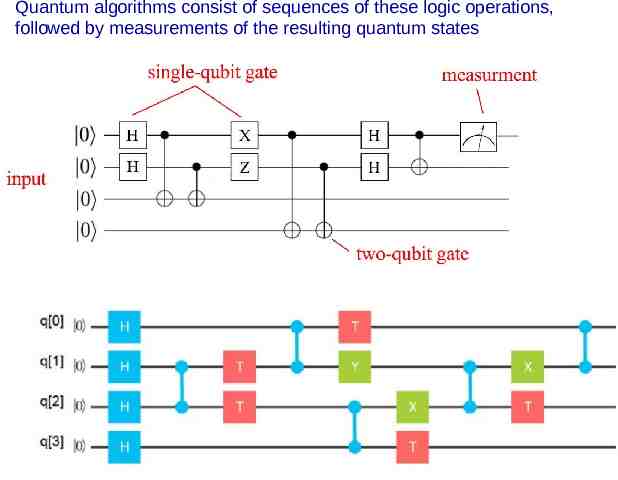
Classical vs. Quantum logic --- gates and algorithms (cont’d) Because the bits are different, the logic operations are different also CLASSICAL LOGIC Classic logic gates operate on discrete binary bits --- there are 7 types of logic gates: Classical algorithms consist of sequences of these logic operations, sometimes performed in parallel in large computers

Classical vs. Quantum logic --- gates and algorithms (cont’d) QUANTUM LOGIC Quantum logic gates operate on single qubits and pairs of qubits

Classical vs. Quantum logic --- gates and algorithms (cont’d) A few other important differences: 1. Quantum gates are reversible --- classical gates are not. That means that the input data is destroyed in the classical operations but is retained in the quantum system 2. Classical gates (if they work) give an exact result --- quantum gates give superpositions of states which are characterized by probabilities That means (1) that you need “high-fidelity” readouts of the state that can distinguish which state the system is in after an operation, and (2) even with perfect fidelity that you need to work with ensembles and do enough measurements to get the final state 3. You need to implement “error-correcting codes” to mitigate accumulated measurements That means that there is an “overhead cost”, i.e. to make N functioning qubits, you may need many more physical qubits --- that overhead depends on the system but can be 10-1000 times* * This is one of prime motivations of topologically-protected qubit platforms since it is proposed that these give error-free operations that will eliminate the need for error-corrections (that is only partially true)

Quantum algorithms consist of sequences of these logic operations, followed by measurements of the resulting quantum states

https://towardsdatascience.com/demystifying-quantum-gates-one-qubit-at-a-time-54404ed80640 If you want to get into quantum computing, there’s no way around it: you will have to master the cloudy concept of the quantum gate. Like everything in quantum computing, not to mention quantum mechanics, quantum gates are shrouded in an unfamiliar fog of jargon and matrix mathematics that reflects the quantum mystery. My goal in this post is to peel off a few layers of that mystery. But I’ll save you the suspense: no one can get rid of it completely. At least, not in 2019. All we can do today is reveal the striking similarities and alarming differences between classical gates and quantum gates, and explore the implications for the near and far future of

Superconducting devices for Quantum Computing Intrinsic low temperature quantum system Characteristic energies and dynamics are well-understood Good control of fabrication and measurement schemes Easy to control and couple qubits Hard to isolate due to many degrees of freedom QUBIT rf SQUID Measurement dc SQUID Al device measurements at 10mK TU Delft

Requirements for quantum computation (DiVincenzo criteria) 1. Scalable physical system of qubits qubit quantum two-level system bit classical two-level system 0 and 1 Superposition: 0 or 1 a 0 b 1 1 Two qubits --- entanglement : A 00 B 01 C 10 D 11 2. Ability to initialize qubits into a particular quantum state initialization at the start of computation supply of qubits in low entropy state for quantum error correction 0 E1 E0 0 1 q

3. Universal set of quantum gates Classical computer all operations from NOT and exclusive-OR Quantum computer all operations from single qubit rotations and the two-qubit controlled-NOT U j e Quantum algorithm sequence of unitary transformations iH j t / 4. Qubit-specific measurement capability a 0 b 1 Quantum measurement: probability of 0 a 2 probability of 2 1 b 1 a 2 Need to measure the state of each qubit without perturbing the state of the others Ideal if the measurement does not destroy the quantum state of the measured qubit also non-demolition Figure of merit quantum efficiency ( 100%)

5. Long decoherence times Effect of the environment entangles system with the environment (bad) or, makes a measurement on the system Decoherence time criterion is hard to define depends on specific system and type of measurement to be made, but must be: “long enough that the uniquely quantum features of the computation have a chance to come into play” System must maintain phase coherence during the execution of sequences of logic operations ( 104 –105) , but not for the duration of the entire calculation Quantum error correction (Shor, 1996) Implications: reduce internal dissipation of the system isolate system as much as possible from the environment

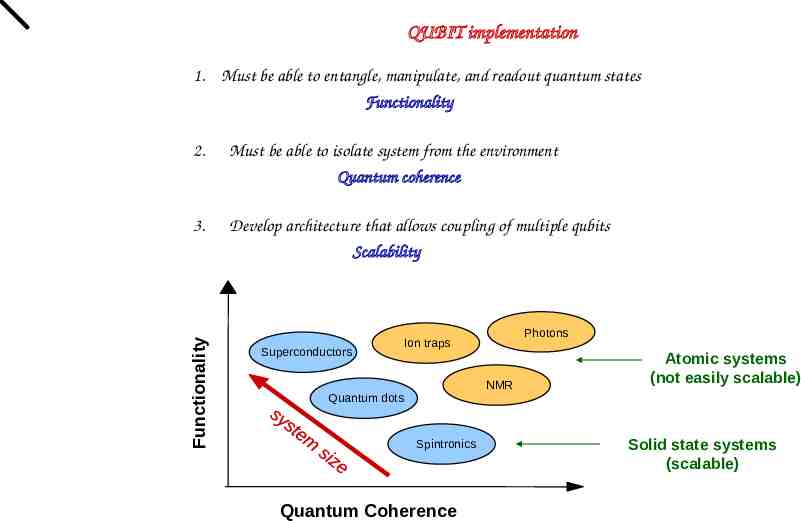
QUBIT implementation 1. Must be able to entangle, manipulate, and readout quantum states Functionality Must be able to isolate system from the environment Quantum coherence 3. Develop architecture that allows coupling of multiple qubits Scalability Functionality 2. Superconductors Photons Ion traps NMR Quantum dots Spintronics Quantum Coherence Atomic systems (not easily scalable) Solid state systems (scalable)

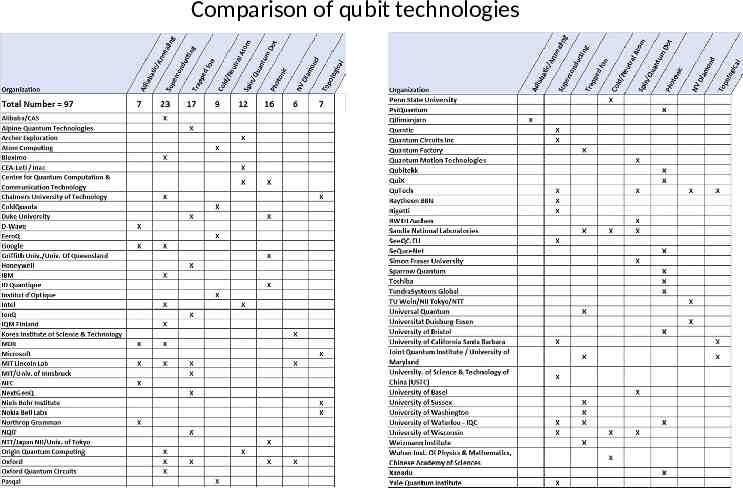
Comparison of qubit technologies

https://www.ibm.com/quantum-computing/