Thought Who is unhappy at only having one mouth? And who is not

Thought Who is unhappy at only having one mouth? And who is not unhappy at having only one eye? Probably no man ever ventured to mourn at not having three eyes. But any one is inconsolable at having none. (Blaise Pascal, Pensees)

Families of Algorithms Elegant Design Principles Divide-and-Conquer Graph Exploration Greedy Choice Drawback: only usable on very specific types of problems “Sledgehammers of the algorithms craft” Dynamic Programming Linear Programming

Recall Divide & Conquer Five pillars of Divide and Conquer algorithms: How to divide into sub-problems? Conquer through recursion How to recombine sub-results? When to stop dividing? Analysis using Master Theorem or Recurrence Relations

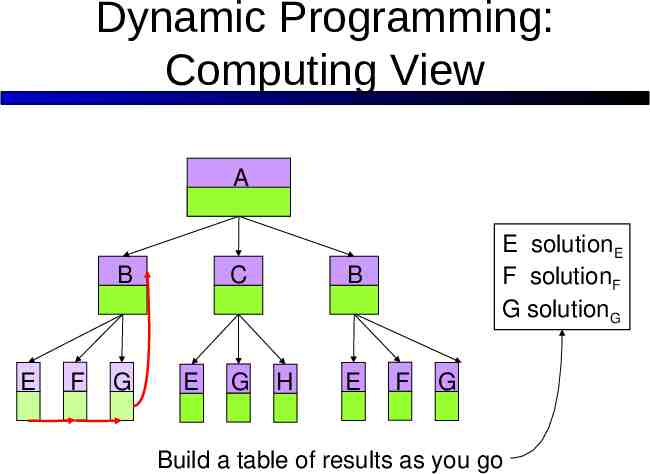
Dynamic Programming: Computing View Not every sub-problem is new. Save time: retain prior results.

Dynamic Programming: Computing View A B E F G C E G B H E F G

Dynamic Programming: Computing View A B E F G C E G B H E F G start solving sub-problems at the bottom.

Dynamic Programming: Computing View A B E F G C E G E solutionE F solutionF G solutionG B H E F G Build a table of results as you go

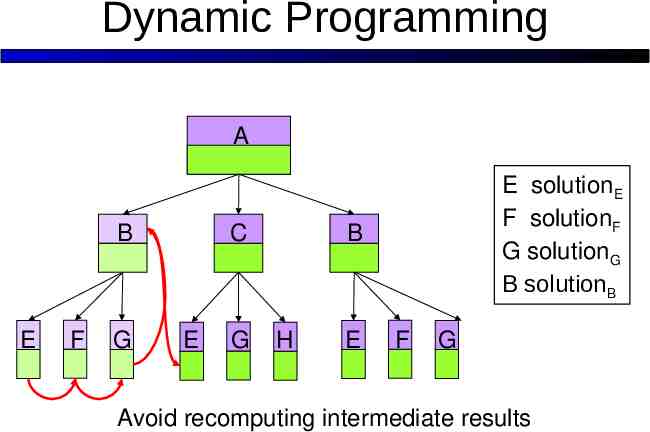
Dynamic Programming A B E F G C E G E solutionE F solutionF G solutionG B solutionB B H E F G Avoid recomputing intermediate results

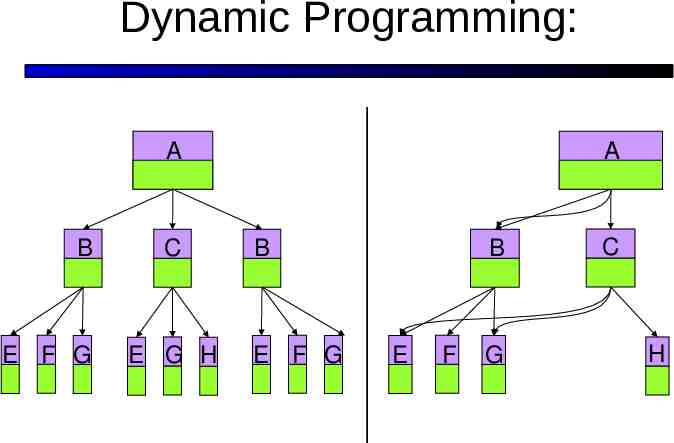
Dynamic Programming: A B E F G C E G H A B E F G B E F G C H

DP: Graph View Nodes When to connect What to analyze Which algorithm?

DP: Graph View Longest Increasing Subsequence Version Nodes: numbers Edges: a b iff a b What to analyze: what is the longest path through the graph? Which algorithm? Variation on Dijkstra’s

DP: Math View There is an ordering on the subproblems, and a relation that shows how to solve a subproblem given the answers to smaller subproblems, that is, subproblems tat appear earlier in the ordering. What would you call such a relation?

DP: Rec. Relation View Longest Increasing Subsequence Version L(j) 1 max{L(i): (i,j) in E} Where j an index in the original list and starts at 0. - Note how L(2) might depend on L(1). - Note how these dependencies are edges in the graph-view. - Note how these dependencies allow you to store and reuse previous results.

Shortest Edit Sequence Given two strings Return min. number of edit operations needed to align them. String 1 is n characters, string 2 is m characters. How many edit sequences are possible? Generate all of them, check if the work, keep the shortest one that works.

DP: Shortest Edit Sequence Or, try to find a recurrence relation. Or, try to write it is a DAG (not particularly helpful for this problem) Or, identify subproblems which can be stored and re-used.

Shortest Edit Sequence E(i,j) min {1 E(i-1,j), 1 E(i,j-1), diff (i,j) E(i-1,j-1)} replacement Delete a letter

Shortest Edit Sequence E(i,j) min {1 E(i-1,j), 1 E(i,j-1), diff (i,j) E(i-1,j-1)}

DP: Gene sequence alignment Insertion, deletion, mutation Costs based loosely on biology. Mutation 1 point Insertion/deletion 5 points Match -3 points

Example: Binomial Coefficient How many ways are there to choose k items from a set of n items? n n! C (n, k ) k k !(n k )! 1 n-1 n 1 k-1 k 0 if k 0 or k n if 0 k n otherwise

Example: C(5,3) 1 n C (n, k ) k if k 0 or k n n-1 n 1 k-1 k 0 if 0 k n otherwise C(5,3) C(4,2) C(3,1) C(2,0) C(2,1) C(4,3) C(3,2) C(3,2) C(2,1) C(2,2) C(2,1) C(2,2) C(1,0) C(1,1) C(1,0) C(1,1) 1 1 1 1 1 C(1,0) C(1,1) 1 1 1 C(3,3) 1 1 (C(n,k))

C(5,3) C(5,3) C(4,2) C(3,1) C(2,0) C(4,3) C(3,2) C(2,1) C(2,2) C(1,0) C(1,1) Does this look familiar? How about if you turn it upside down? C(3,3)

Pascal’s Triangle Blaise Pascal (1623-1662) Second person to invent the calculator Religious philosopher Mathematician and physicist

From Recurrence to Table Start with a recurrence relation Turn it into a table. Figure out what the variables are Use them to index the rows and columns. Figure out what the base case is. Do that first in the table Then figure out the inductive step and work up to the final answer.

1 n C (n, k ) k 0 0 1 2 3 4 5 if k 0 or k n n-1 n 1 k-1 k 0 1 2 if 0 k n otherwise 3

1 n C (n, k ) k 0 0 1 2 3 4 5 if k 0 or k n n-1 n 1 k-1 k 0 1 2 if 0 k n otherwise 3

Making Change using DP Given j, what’s the fewest coins required to make j in change? Example: m 4 different denominations of coins. Values d [1 2 4 7] Compute how many coins needed to make change for value j: coins(d,j) Does greedy work with d? Goal: Write Dynamic Programming algorithm. Hint: do something like what we did for binomial coefficient.

DP Coins Given n types of coins (unlimited supplies) Make c in change. What’s min. # of coins required? Formulated as a DP problem.

DP Coins Given n types of coins (unlimited supplies) Make j in change. What’s min. # of coins required? Formulated as a DP problem. i is the number of coin types remaining.

Recursive Function Given j, what’s the fewest coins required to make j in change? Recursive function: c[i,j] number of coins needed to make j cents of change using coins of type 1 through i. Derive algorithm from recursive function Modify resulting algorithm for space and time.

Making Change Given j, what’s the fewest “coins” required to make j in change? j Amount i 0 1 2 3 4 5 6 7 senum 1 0 1 2 3 4 5 6 7 seon 2 shum 4 limnah 7 c[i,j] min. number of “coins” to make j change with coins 1.i.

Making Change j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 shum 4 limnah 7 c[i,j] min. number of coins to make j change with coins 1.i.

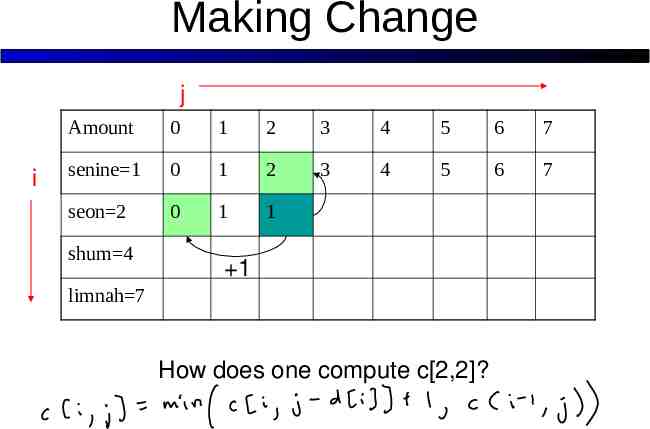
Making Change j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 ? shum 4 limnah 7 How does one compute c[2,2]?

Making Change j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 shum 4 1 limnah 7 How does one compute c[2,2]?

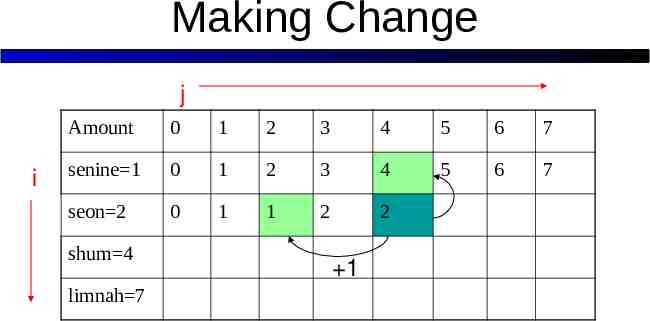
Making Change j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 shum 4 1 limnah 7 How does one compute c[2,2]?

Making Change j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 shum 4 limnah 7 1

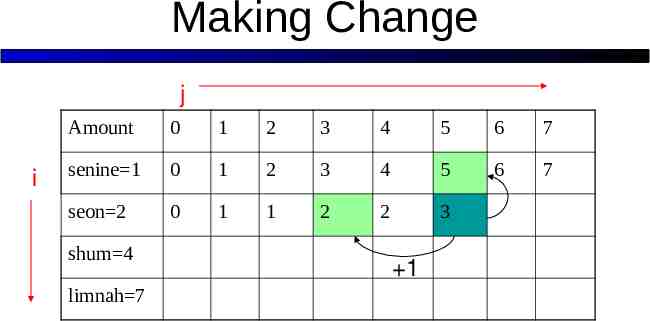
Making Change j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 shum 4 limnah 7 1

Making Change j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 shum 4 limnah 7 1

Making Change j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 3 4 shum 4 0 1 1 2 1 2 2 3 limnah 7 0 1 1 2 1 2 2 1

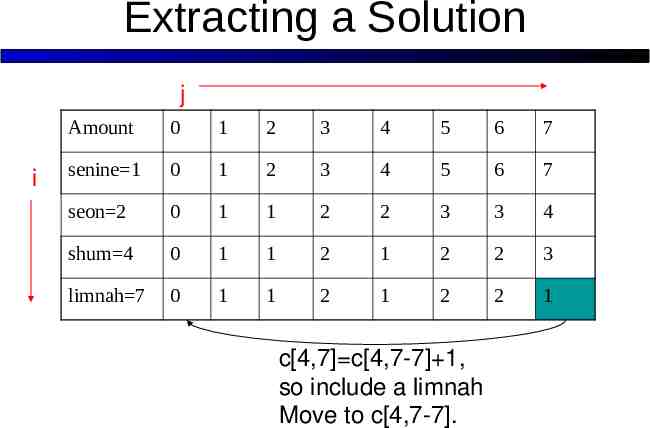
Extracting a Solution j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 3 4 shum 4 0 1 1 2 1 2 2 3 limnah 7 0 1 1 2 1 2 2 1 c[4,7] c[4,7-7] 1, so include a limnah Move to c[4,7-7].

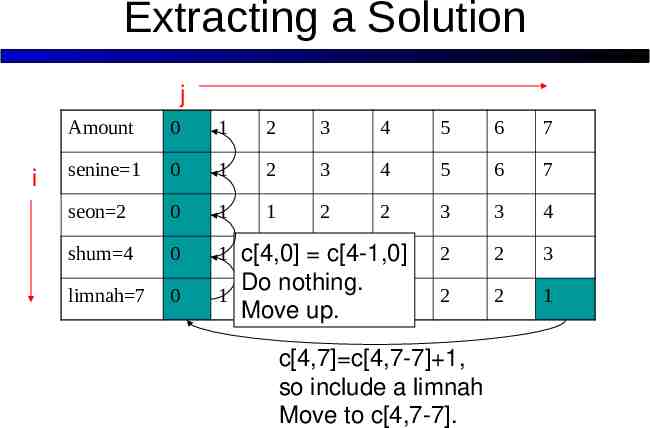
Extracting a Solution j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 3 4 shum 4 0 1 c[4,0] 2 1 3c[4-1,0] 2 2 3 limnah 7 0 1 Do nothing. 2 3 1 Move up. 2 2 1 c[4,7] c[4,7-7] 1, so include a limnah Move to c[4,7-7].

Extracting a Solution j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 3 4 shum 4 0 1 c[4,0] 2 1 3c[4-1,0] 2 2 3 limnah 7 0 1 Do nothing. 2 3 1 Move up. 2 2 1 c[4,7] c[4,7-7] 1, so include a limnah Move to c[4,7-7].

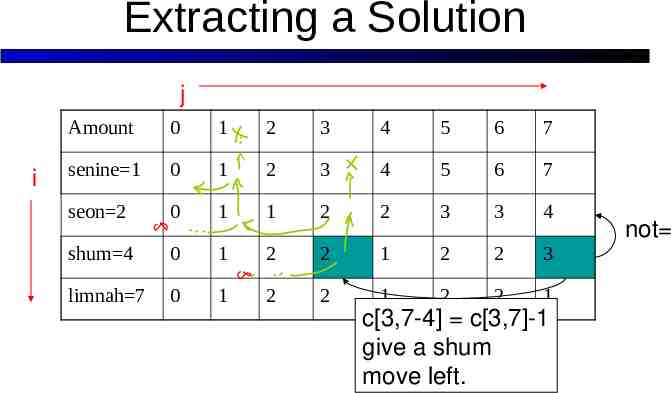
Extracting a Solution j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 3 4 shum 4 0 1 2 2 1 2 2 3 limnah 7 0 1 2 2 1 2 2 1 c[3,7-4] c[3,7]-1 give a shum move left. not

Extracting a Solution j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 3 4 shum 4 0 1 2 2 1 2 2 3 limnah 7 0 1 2 2 1 2 2 1 c[3,7-4] c[3,7]-1 give a shum move left. not

Extracting a Solution j i Amount 0 1 2 3 4 5 6 7 senine 1 0 1 2 3 4 5 6 7 seon 2 0 1 1 2 2 3 3 4 shum 4 0 1 2 2 1 2 2 3 limnah 7 0 1 2 2 1 2 2 1 How much space? How much time?

Algorithm in Pseudo-code function coins(d, N) Input: Array d[1.n] specifies the coinage; N is the number of units for which to make change Output: Minimum number of coins needed to make change for N units using coins from d array c[1.n,0.N] for i 1 to n do c[i,0] 0 for i 1 to n do for j 1 to N do if i 1 and j d[i] then c[i,j] infinity else if i 1 then c[i,j] 1 c[1,j-d[1]] else if j d[i] then c[i,j] c[i-1,j] else c[i,j] min(c[i-1,j],1 c[i,j-d[i]]) return c[n,N]

Pre-computing vs. on-the-fly Like lazy vs. eager evaluation Pre-computing build table, then analyze results. On-the-fly build table entries as you go

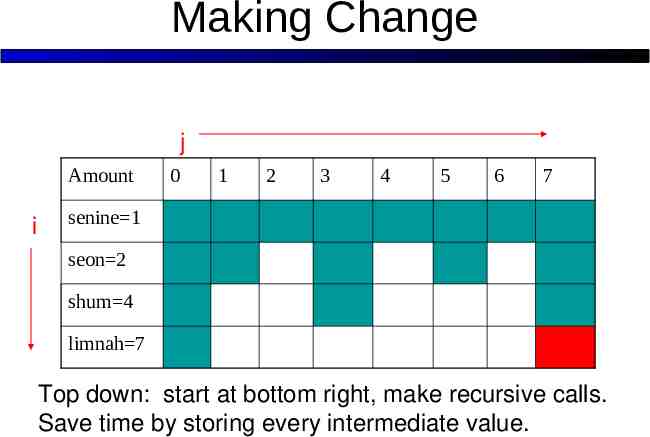
Making Change: Top Down j Amount i 0 1 2 3 4 5 6 7 senine 1 seon 2 shum 4 limnah 7 Top down: start at bottom right, make recursive calls.

Making Change j Amount i 0 1 2 3 4 5 6 7 senine 1 seon 2 shum 4 limnah 7 Top down: start at bottom right, make recursive calls. Save time by storing every intermediate value.

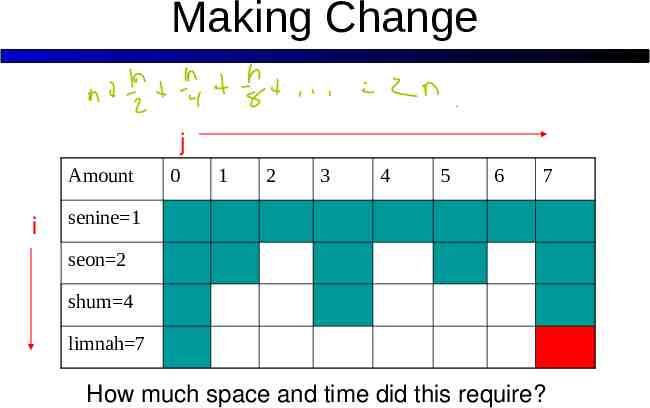
Making Change j Amount i 0 1 2 3 4 5 6 7 senine 1 seon 2 shum 4 limnah 7 How much space and time did this require?

Comparison How does DP algorithm compare to greedy? speed space correctness simplicity