The Pythagorean Theorem Presented by: Tanya Van Dam Kalles Junior

The Pythagorean Theorem Presented by: Tanya Van Dam Kalles Junior High Algebra 2 Spring 2000

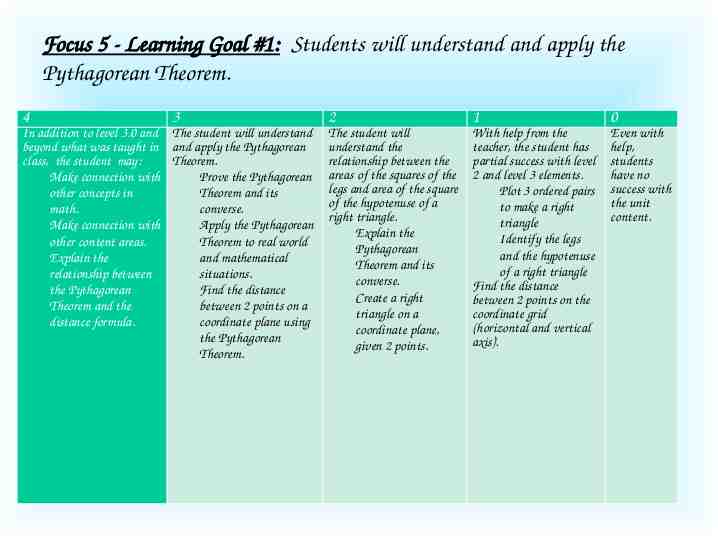
Focus 5 - Learning Goal #1: Students will understand and apply the Pythagorean Theorem. 4 3 2 1 0 In addition to level 3.0 and beyond what was taught in class, the student may: Make connection with other concepts in math. Make connection with other content areas. Explain the relationship between the Pythagorean Theorem and the distance formula. The student will understand and apply the Pythagorean Theorem. Prove the Pythagorean Theorem and its converse. Apply the Pythagorean Theorem to real world and mathematical situations. Find the distance between 2 points on a coordinate plane using the Pythagorean Theorem. The student will understand the relationship between the areas of the squares of the legs and area of the square of the hypotenuse of a right triangle. Explain the Pythagorean Theorem and its converse. Create a right triangle on a coordinate plane, given 2 points. With help from the teacher, the student has partial success with level 2 and level 3 elements. Plot 3 ordered pairs to make a right triangle Identify the legs and the hypotenuse of a right triangle Find the distance between 2 points on the coordinate grid (horizontal and vertical axis). Even with help, students have no success with the unit content.

Pythagoras Lived in southern Italy during the sixth century B.C. Considered the first true mathematician Used mathematics as a means to understand the natural world First to teach that the earth was a sphere that revolves around the sun

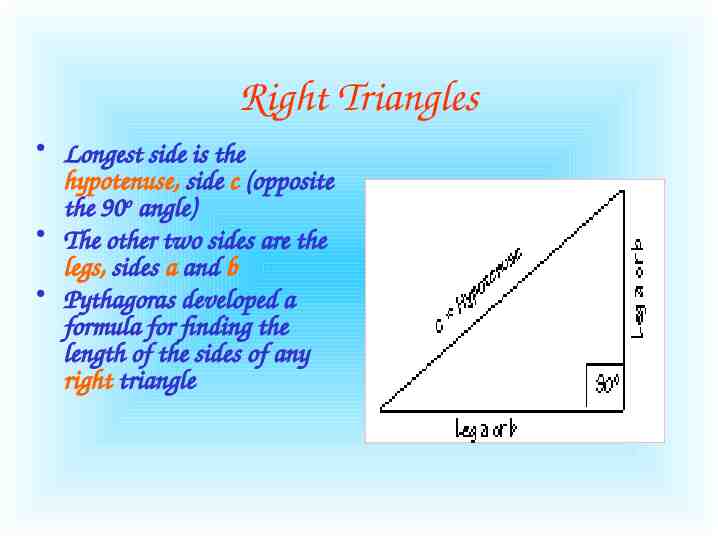
Right Triangles Longest side is the hypotenuse, side c (opposite the 90o angle) The other two sides are the legs, sides a and b Pythagoras developed a formula for finding the length of the sides of any right triangle

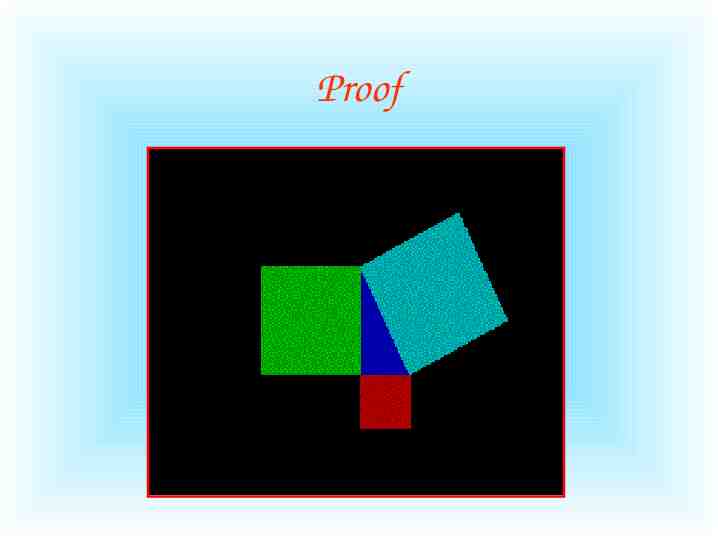
The Pythagorean Theorem “For any right triangle, the sum of the areas of the two small squares is equal to the area of the larger.” a2 b2 c2

Proof

Applications The Pythagorean theorem has far-reaching ramifications in other fields (such as the arts), as well as practical applications. The theorem is invaluable when computing distances between two points, such as in navigation and land surveying. Another important application is in the design of ramps. Ramp designs for handicap-accessible sites and for skateboard parks are very much in demand.

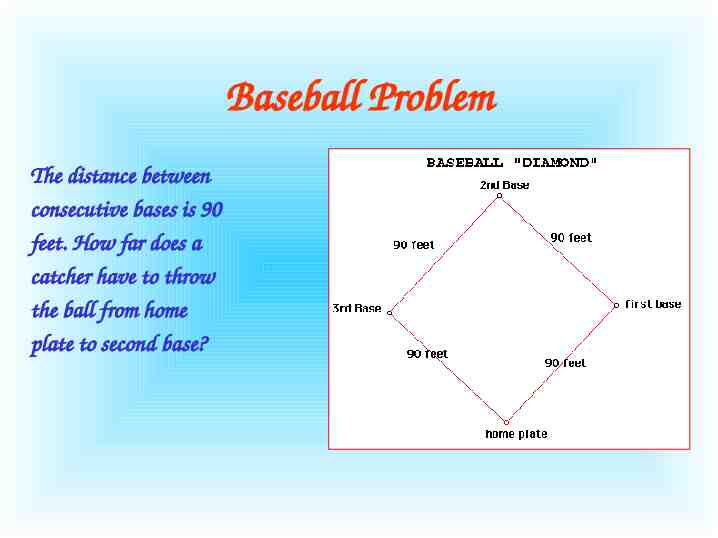
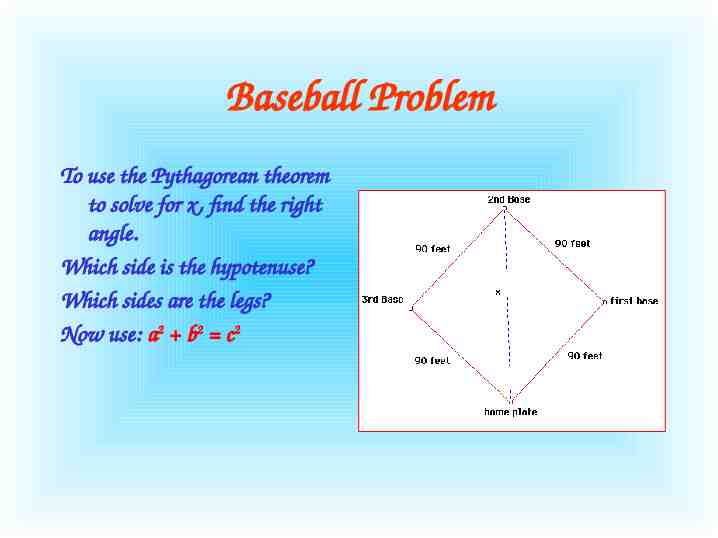
Baseball Problem A baseball “diamond” is really a square. You can use the Pythagorean theorem to find distances around a baseball diamond.

Baseball Problem The distance between consecutive bases is 90 feet. How far does a catcher have to throw the ball from home plate to second base?

Baseball Problem To use the Pythagorean theorem to solve for x, find the right angle. Which side is the hypotenuse? Which sides are the legs? Now use: a2 b2 c2

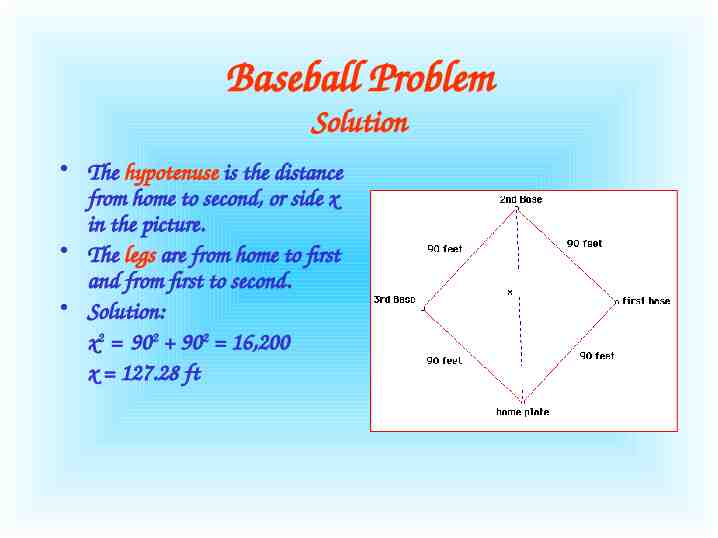
Baseball Problem Solution The hypotenuse is the distance from home to second, or side x in the picture. The legs are from home to first and from first to second. Solution: x2 902 902 16,200 x 127.28 ft

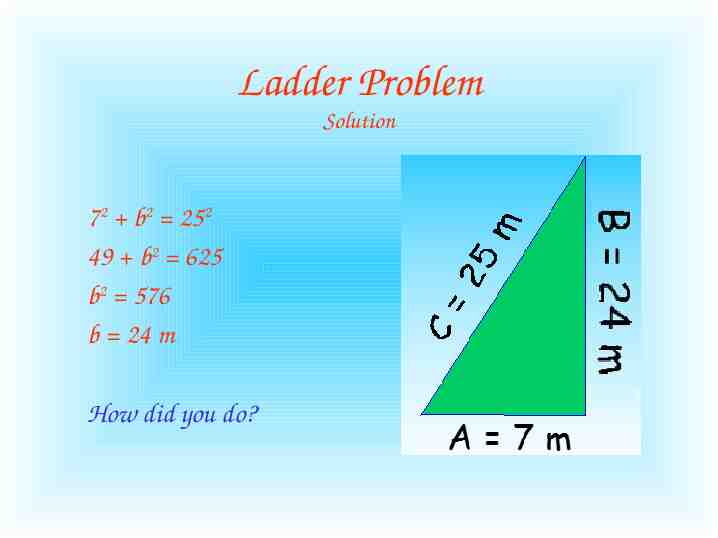
Ladder Problem A ladder leans against a second-story window of a house. If the ladder is 25 meters long, and the base of the ladder is 7 meters from the house, how high is the window?

Ladder Problem Solution First draw a diagram that shows the sides of the right triangle. Label the sides: – Ladder is 25 m – Distance from house is 7 m Use a2 b2 c2 to solve for the missing side. Distance from house: 7 meters

Ladder Problem Solution 72 b2 252 49 b2 625 b2 576 b 24 m How did you do? B

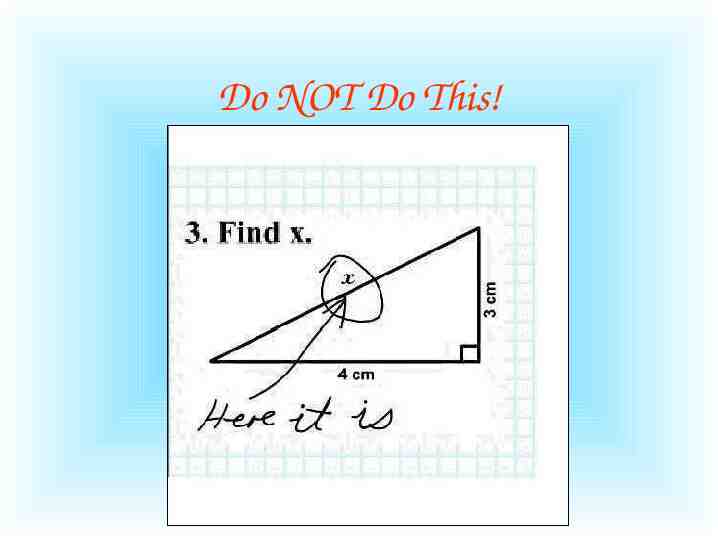
Do NOT Do This!

Sources Great info on the Pythagorean theorem, Pythagoras, and other math-related topics: – The Baseball Problem – Pythagoras of Samos – Pythagoras Playground – Microsoft Encarta 2000