Testing String Theory with CMB Renata Kallosh Stanford CIfAR, Whistler

Testing String Theory with CMB Renata Kallosh Stanford CIfAR, Whistler , May 10, 2007 Based on R. K., A. Linde, 0704.0647, R. K. , hep-th/0702059, R. K., M. Soroush, N. Sivanandam, work in progress

There was no explanation of inflation and dark energy in string theory until 2003 2003: Flux compactification and moduli stabilization: landscape of vacua, some of them are de Sitter vacua Simplest model: KKLT stabilization of the volume of the internal six-dimensional space

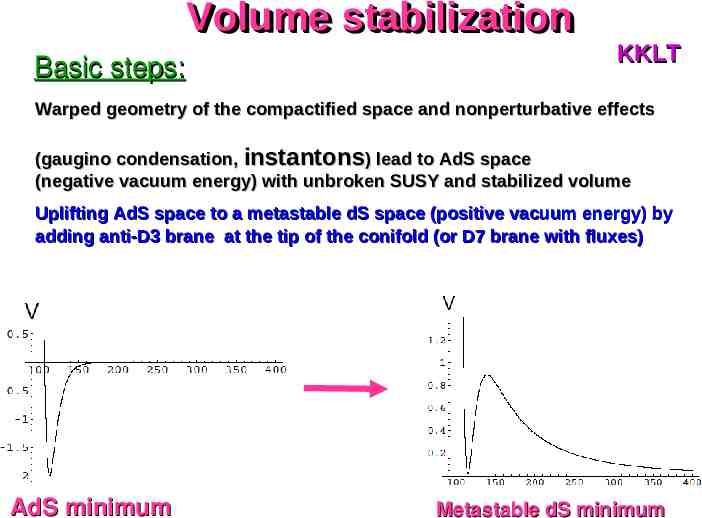
Volume stabilization Basic steps: KKLT Warped geometry of the compactified space and nonperturbative effects (gaugino condensation, instantons) lead to AdS space (negative vacuum energy) with unbroken SUSY and stabilized volume Uplifting AdS space to a metastable dS space (positive vacuum energy) by adding anti-D3 brane at the tip of the conifold (or D7 brane with fluxes) AdS minimum Metastable dS minimum

Now string theory has one explanation of dark energy: metastable cosmological constant with equation of state So far in agreement with the data. No other compelling models are available There are several models of inflation in string theory. They are flexible enough to describe but typically predict low level of gravitational waves and low non-gaussianity. They may explain light cosmic strings. Observations of GW, cosmic strings or non-gaussianity can help us to test string theory Here we will focus of GW

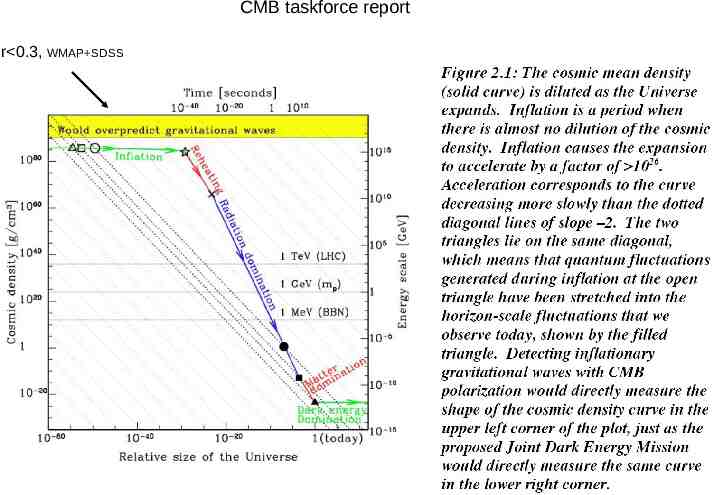
CMB taskforce report r 0.3, WMAP SDSS

Several possibilities: After we fit ns, we may find: Tensor modes detected: Great challenge for string theory! No tensor modes No cosmic strings Cosmic strings detected: No problem for string theory, a welcome effect, a potential window into physics at the string scale Non-gaussianity detected: No non-gaussianity Cosmology Planck Mass of gravitino ? some solutions maybe possible Particle physics LHC

What if tensor modes are detected? Planck science mission blue book Planck will be sensitive to a B-mode polarization signal if the scalar-tensor ratio is greater than a few per cent. This marks an important science goal for Planck. A detection would imply that the inflaton changed by factors of unity or more in Planck units What will this mean for the fundamental physics, string theory and supergravity? What to expect beyond Planck ?

Experiments taking data now. BICEP QUAD CalTech, JPL UCSD, Berkeley Cardiff, IAS Stanford, CalTech JPL, Cardiff, Chicago, Edinburgh, Maynooth 40' beam 90 & 150 Ghz 5' beam 90 & 150 Ghz High Precision E Mode determination

The Next Generation: 6 Machines! Spider: CalTech, CWRU, ICL, JPL, NIST, UBC, U Toronto SPUD: CalTech, JPL, UCSD, Berkeley, Cardiff, IAS, Toronto polarBear: Berkeley, LBNL, UCSD, McGill Colorado QUIET: Chicago, JPL, Miami, Princeton, CalTech, Columbia, Stanford, Oxford, MPI EBEX: Brown, Cardiff, Columbia,APC, Harvard, IAS, ISAS, McGill, Oxford, UCB/LBNL, UCSD, Minnesota, Toronto, Weizmann Clover: Cambridge, Cardiff, Oxford, NIST, CalTech, UBC

Status: Barth Netterfield All have begun construction All hope to detect r 0.1 All plan to have results by 2011

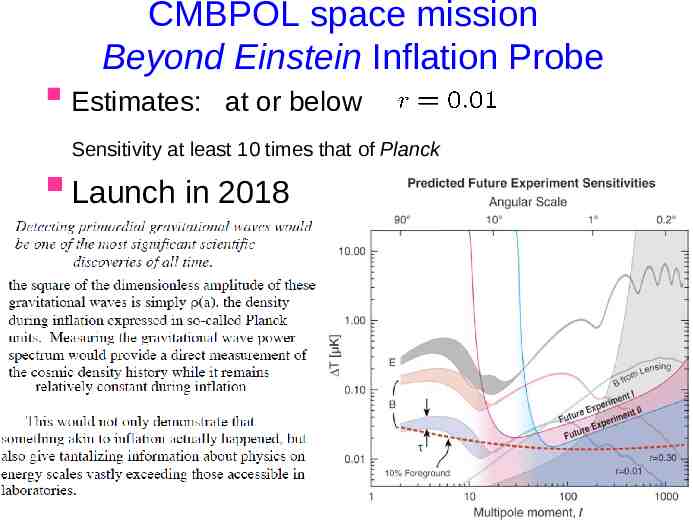
CMBPOL space mission Beyond Einstein Inflation Probe Estimates: at or below Sensitivity at least 10 times that of Planck Launch in 2018

Models of inflation predicting GW Chaotic inflation Natural inflation Assisted inflation: Field theory models Relation to supersymmetry, supergravity, string theory? chaotic inflation with many fields If any of these models are related to string theory/supergravity, it becomes a particularly important issue of the fundamental physics: we will be waiting for new data from A bit of relaxation for N 102n Planck and CMBPOL

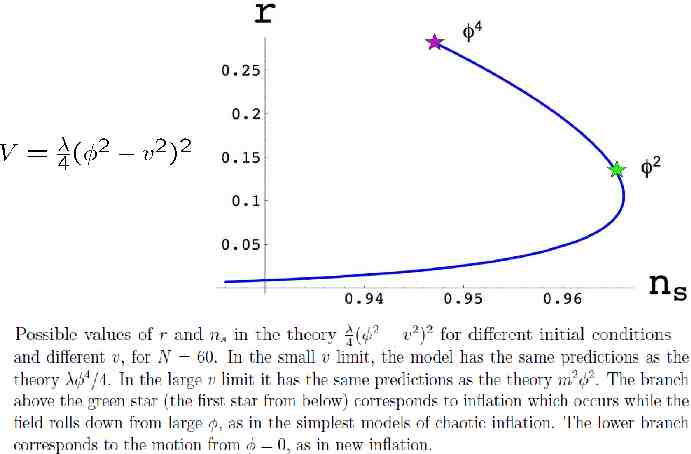
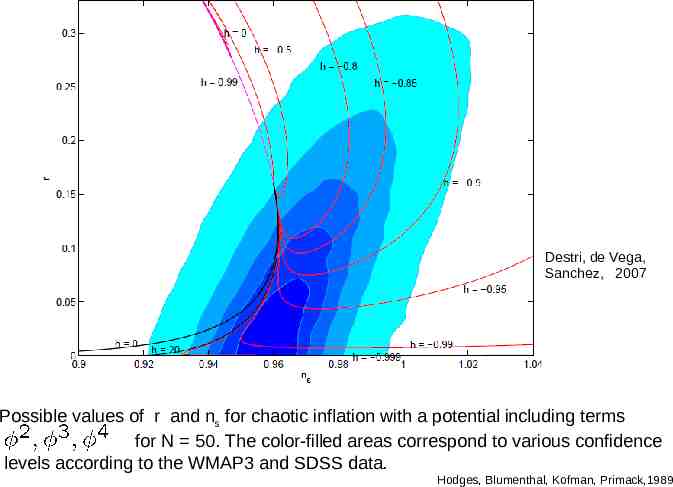
Destri, de Vega, Sanchez, 2007 Possible values of r and ns for chaotic inflation with a potential including terms for N 50. The color-filled areas correspond to various confidence levels according to the WMAP3 and SDSS data. Hodges, Blumenthal, Kofman, Primack,1989

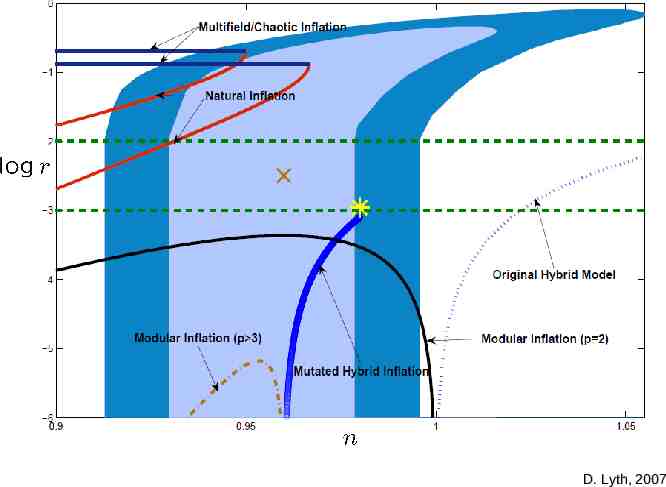
D. Lyth, 2007

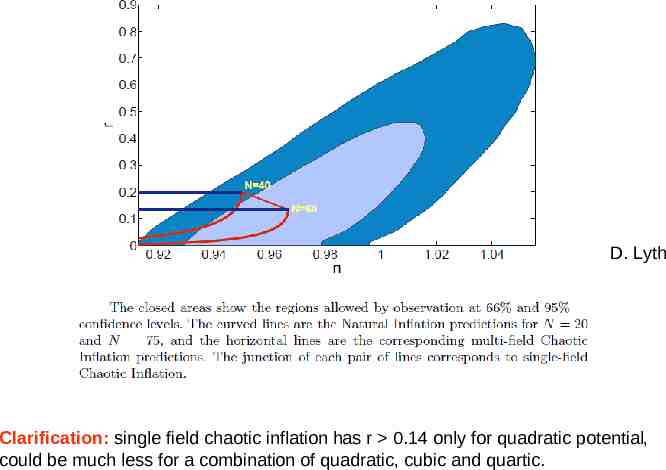
D. Lyth Clarification: single field chaotic inflation has r 0.14 only for quadratic potential, could be much less for a combination of quadratic, cubic and quartic.

After recent debates All known brane inflation models and modular inflation models in string theory predict a non-detectable level of tensor modes These include the known versions of DBI models N-flation model still has to be derived from string theory

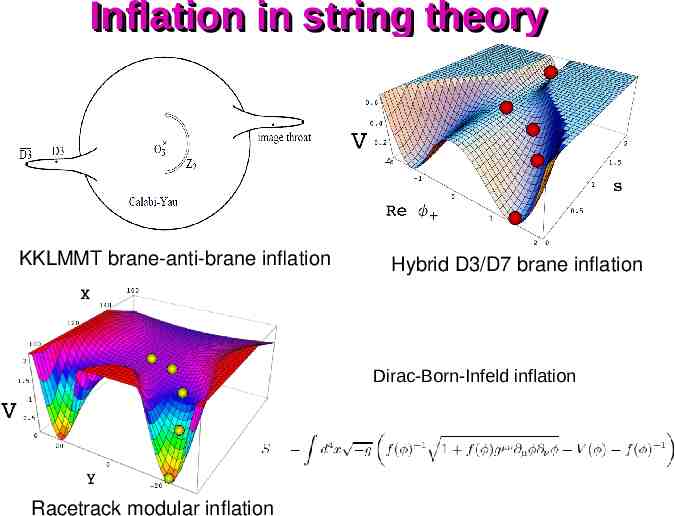
Inflation in string theory KKLMMT brane-anti-brane inflation Hybrid D3/D7 brane inflation Dirac-Born-Infeld inflation Racetrack modular inflation

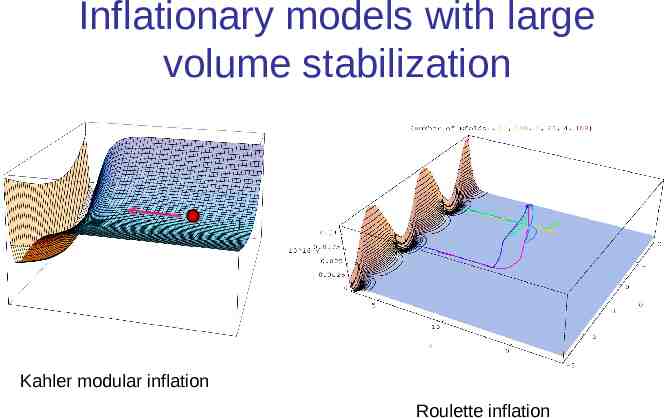
Inflationary models with large volume stabilization Kahler modular inflation Roulette inflation

The goal of cosmology community for a long time was to reconstruct from the data some information on the inflationary potential This is still a valuable goal. However, in the context of string theory and effective N 1 supergravity the goal is to get some information on the Kähler potential and the Superpotential , Generic potential of N 1 supergravity depends on some number of complex scalar fields which have a geometric meaning of coordinates in Kähler geometry D-terms

Chaotic inflation in supergravity Main problem: Canonical Kähler potential is Therefore the potential blows up at large φ , and slow-roll inflation is impossible: Too steep, no inflation

A solution: shift symmetry Kawasaki, Yamaguchi, Yanagida 2000 Equally good Kähler potential and superpotential The potential is very curved with respect to X and Re φ, so these fields vanish. But Kähler potential does not depend on The potential of this field has the simplest form, without any exponential terms, even including the radiative corrections:

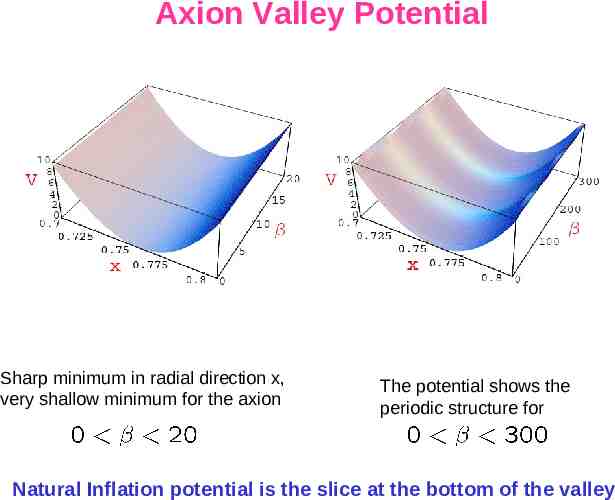
R. K. 2007 Axion Valley Model: Effective Natural Inflation in Supergravity Shift symmetric quadratic Kähler potential KKLT-type superpotential The potential after the KKLT-type uplifting has a minimum at some value of the radial variable x0. The radial direction is very steep. At this minimum the potential is

Axion Valley Potential Sharp minimum in radial direction x, very shallow minimum for the axion The potential shows the periodic structure for Natural Inflation potential is the slice at the bottom of the valley

There are models of inflation in supergravity which predict tensor modes with In all known cases they have shiftsymmetric quadratic Kähler potentials We will have to wait till 2018 before we know if such supergravity models are valid We anticipate learning new things about supersymmetry at this time

In string theory the computable Kähler potentials in known cases of CalabiYau compactification have shift symmetry However, they are logarithmic, not quadratic These models predict undetectably small tensor modes in inflation.

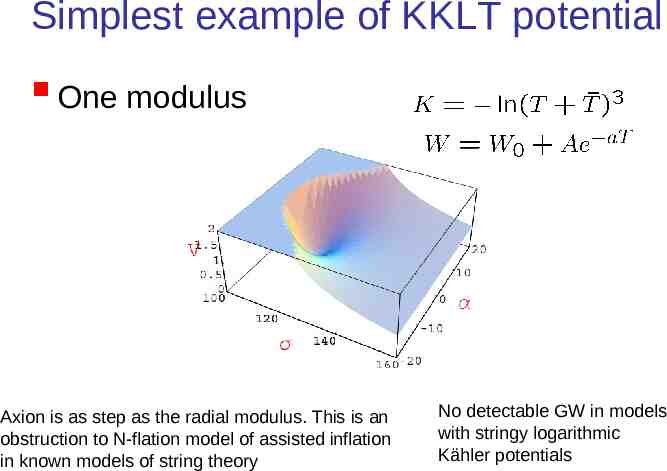
Simplest example of KKLT potential One modulus Axion is as step as the radial modulus. This is an obstruction to N-flation model of assisted inflation in known models of string theory No detectable GW in models with stringy logarithmic Kähler potentials

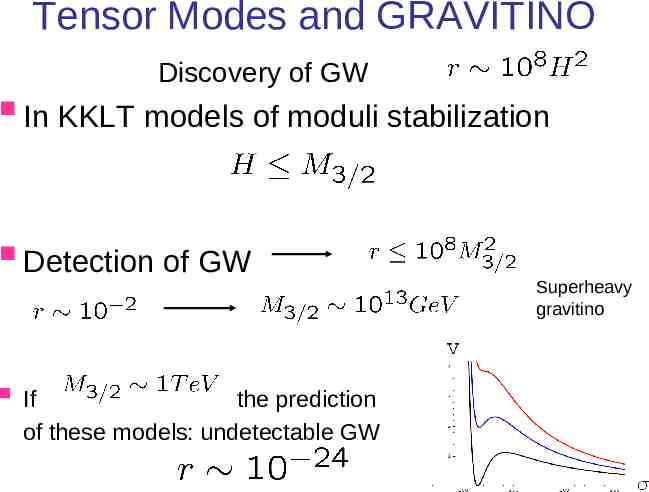
Tensor Modes and GRAVITINO Discovery of GW In KKLT models of moduli stabilization Detection of GW If the prediction of these models: undetectable GW Superheavy gravitino

In the context of inflation in string theory and supergravity, the detection or nondetection of the tensor modes from inflation is of crucial importance! At the present level of understanding there seem to be a unique way to read the features of the Kähler potential from the sky. The mass of the gravitino is tied to future detection or non-detection of the tensor modes in the known string theory models.