Teaching Secondary Mathematics Module 2: Overview of the Mathematics

Teaching Secondary Mathematics Module 2: Overview of the Mathematics Developmental Continuum P-10 2

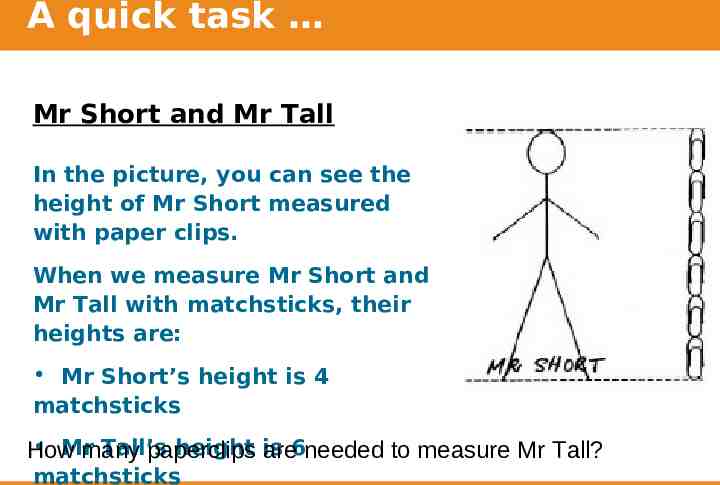
A quick task Mr Short and Mr Tall In the picture, you can see the height of Mr Short measured with paper clips. When we measure Mr Short and Mr Tall with matchsticks, their heights are: Mr Short’s height is 4 matchsticks Mr Tall’s height is How many paperclips are6needed to measure Mr Tall? matchsticks

Discussion Points Explain your solution to your partner? How might you present this task to a group of students? What misconceptions do you imagine might be uncovered through this task?

Purpose of the Continuum Improve student learning The Continuum identifies evidence based indicators of progress consistent with the standards and progression points The Continuum provides a range of powerful teaching strategies that support purposeful teaching for students with similar learning needs

About The Continuum Resource to support improvement in teaching mathematics Assist teachers with the implementation of the VELS Highlight areas of mathematics with important common misunderstandings Give explicit teaching strategies to meet the learning needs of all students Use international research and Victorian data where possible Created by team from University of Melbourne (K Stacey, H Chick, C Pearn, L Ball, V Steinle), with I Lowe (MAV) and P Sullivan (Monash)

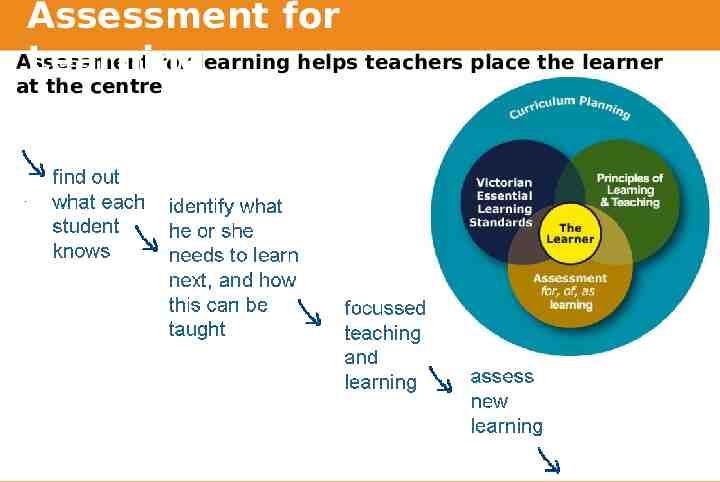
Assessment for Assessment for learning helps teachers place the learner Learning at the centre

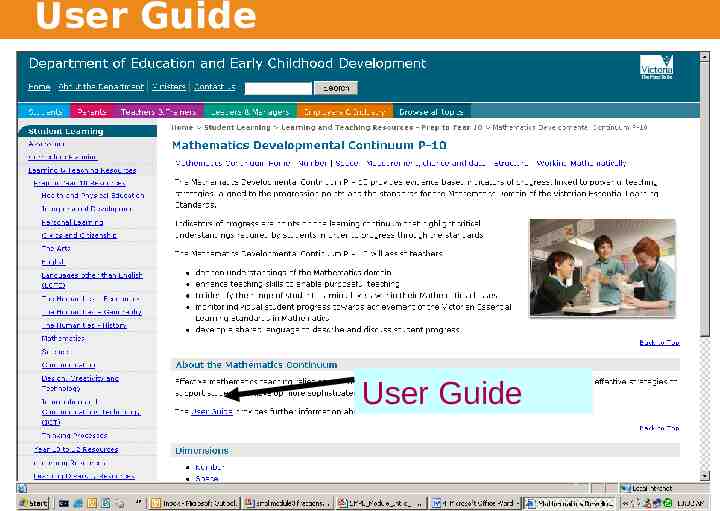
User Guide User Guide

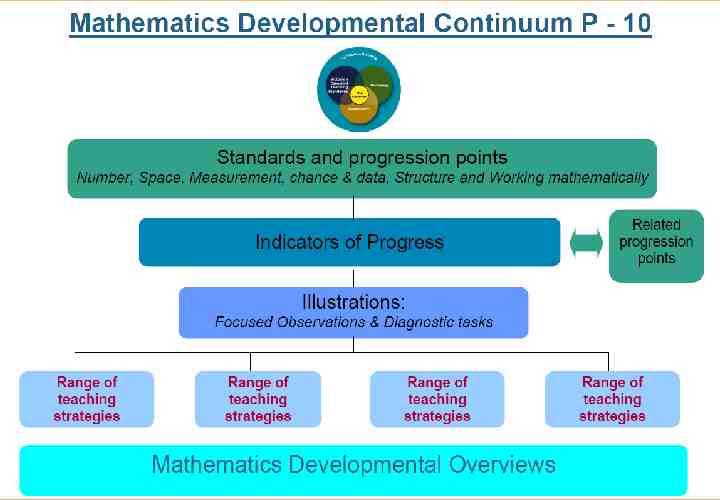
Indicators of progress Points on the learning continuum that highlight critical understandings required by students in order to progress through the standards Indicator refers to both the statement of the new understanding that is required, and also to the complete set of material provided Support teachers’ understanding of student growth Give some background information about the conceptual change, often with further reading Do not cover all content of VELS

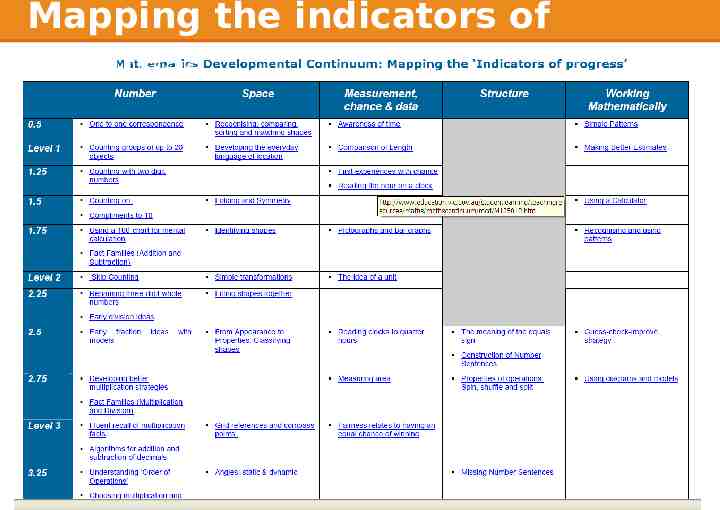
Mapping the indicators of progress

Adding and taking off a percentage: 5.25 Overview:

Adding and taking off a percentage: 5.25 Problem: My football team had 2000 members last year. There has been a 15 % increase in membership this year. How many members are there now? Discuss with a partner how you would solve this problem with a calculator, and if you had to do it mentally, would you solve it differently?

Adding and taking off a percentage: 5.25 Student work sample- illustration This student has correctly found 15% of 2000, and added it on to find the total required to solve this problem in two steps. It appears from this sample of work, he may not know how to solve this problem in one step i.e. multiplying by 1.15.

Adding and taking off a percentage: 5.25 Illustrations in the Maths Continuum can be used for: Identifying the student’s misconceptions – what is the student’s mathematical thinking? Determining the mathematical focus Planning a learning experience Focusing observations and teaching conversations

Adding and taking off a percentage: 5.25 Teaching strategies and activities Specific tasks designed for purposeful teaching Generic ways of how problems of this nature can be effectively addressed Ideas for very specific teaching, which can be used to address this indicator Although there are some resources ready for students to use, the audience for the Continuum is always teachers and not students directly

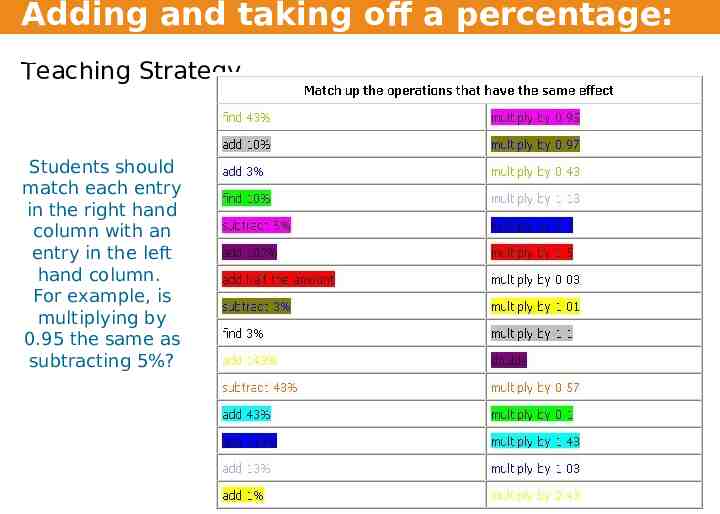
Adding and taking off a percentage: 5.25 Teaching Strategy Students should match each entry in the right hand column with an entry in the left hand column. For example, is multiplying by 0.95 the same as subtracting 5%?

Adding and taking off a percentage: 5.25 Related progression points Each indicator has a linked table giving a selection of progression points to show the developmental progression leading up to and beyond a given indicator

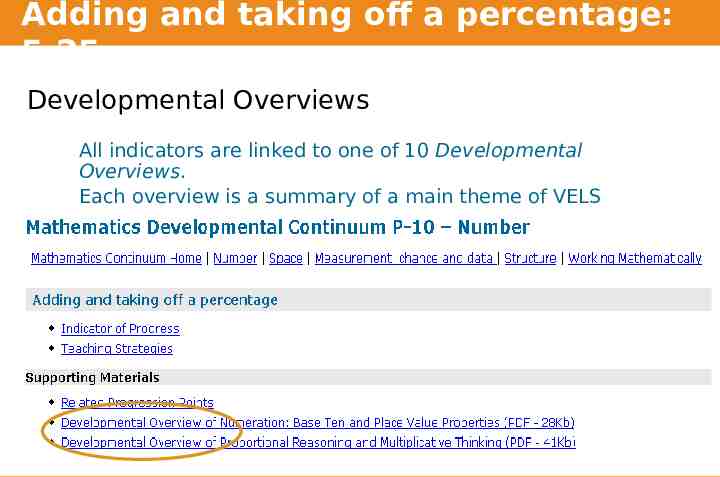
Adding and taking off a percentage: 5.25 Developmental Overviews All indicators are linked to one of 10 Developmental Overviews. Each overview is a summary of a main theme of VELS Mathematics.

Scavenger Hunt activity

Mathematics Developmental Continuum P10 intent To improve student learning “It is through our assessment that we communicate to our pupils those things which we most value.” (David Clarke)

Finding Mathematics Developmental Continuum P-10 Go to the DEECD website and navigate to the Mathematics domain page www.education.vic.gov.au/studentlearning/ teachingresources/maths/mathscontinuum/default.ht m Enter ‘Mathematics Developmental Continuum Victoria’ into any search engine

End of Module 2 This is the last slide of the module Further questions [email protected] Subject field- Teaching Secondary Mathematics