Software Project Management Chapter 6 4th Edition Activity planning

Software Project Management Chapter 6 4th Edition Activity planning 1 The McGraw-Hill Companies, 2005

Scheduling Having – worked out a method of doing the project – identified the tasks to be carried – assessed the time needed to do each task A detailed plan for the project, however, must also include a schedule indicating the start and completion times for each activity. This will enable us to: – Ensure that the appropriate resources will be available precisely when required; – Avoid different activities competing for the same resources at the same time; – Produce a detailed schedule. Showing which staff carry out each activity; – Produce a detailed plan against which actual achievement may be measured; – Produce a timed cash flow forecast; – Re-plan the project during its life to correct drift from the target. 2 The McGraw-Hill Companies, 2005

The Objectives of Activity Planning Providing project and resource schedules Feasibility assessment: Is the project possible within required timescales and resource constraints? Resource allocation: What are the most effective ways of allocating resources to the project. When should the resources be available? Detailed costing: How much will the project cost? we can obtain more detailed estimates of costs and their timing. Motivation: Providing targets and being seen to monitor achievement against targets is an effective way of motivating staff. Coordination: When do the staff in different departments need to be available to work on a particular project and when do staff need to be transferred between projects? 3 The McGraw-Hill Companies, 2005

Identifying Activities There are three approaches to identifying the activities or tasks – The activity-based approach. – The product-based approach. – The hybrid approach. The activity-based approach: – The activity-based approach consists of creating a list of all the activities that the project is thought to involve. – Create a Work Breakdown Structure (WBS). This involves identifying the main (or high-level) tasks required to complete a project and then breaking each of these down into a set of lower-level tasks 4 The McGraw-Hill Companies, 2005

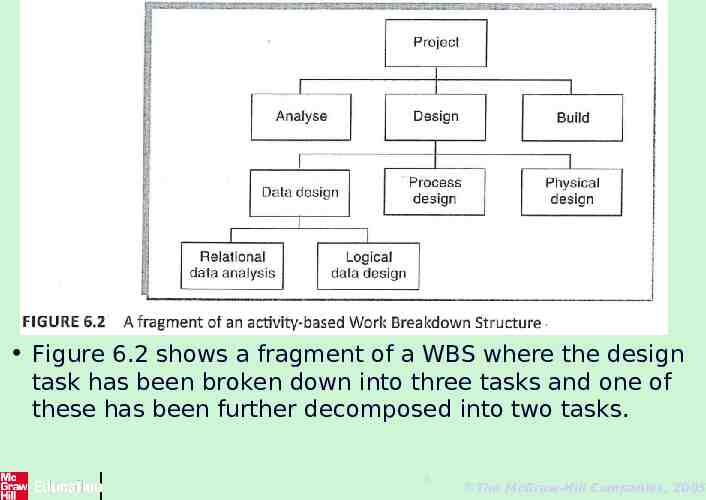
Figure 6.2 shows a fragment of a WBS where the design task has been broken down into three tasks and one of these has been further decomposed into two tasks. 5 The McGraw-Hill Companies, 2005

Identifying activities Product-based approach – It consists of producing a Product Breakdown Structure and a Product Flow Diagram. The PFD indicates, for each product, which other products are required as inputs. The PFD can therefore be easily transformed into an ordered list of activities by identifying the transformations that turn some products into others list the deliverable and intermediate products of project – product breakdown structure (PBS) Identify the order in which products have to be created work out the activities needed to create the products 6 The McGraw-Hill Companies, 2005

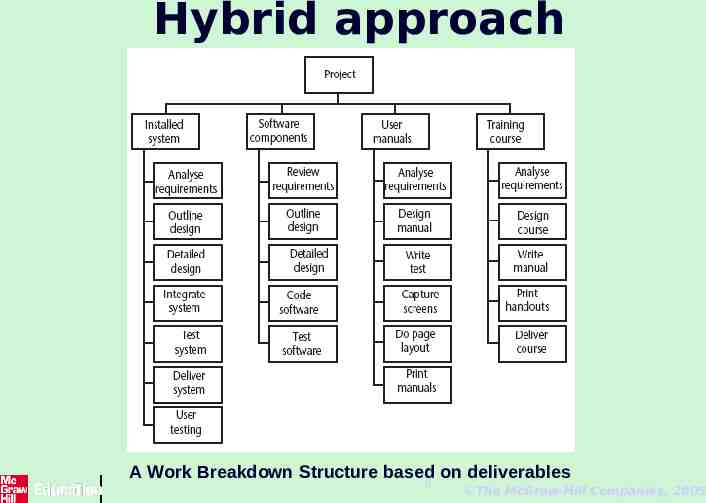
Hybrid approach a WBS may be based upon the project's products as illustrated in Figure 6.5, which is in turn based on a simple list of final deliverables and, for each deliverable, a set of activities required to produce that product. . 7 The McGraw-Hill Companies, 2005

Hybrid approach A Work Breakdown Structure based on deliverables 8 The McGraw-Hill Companies, 2005

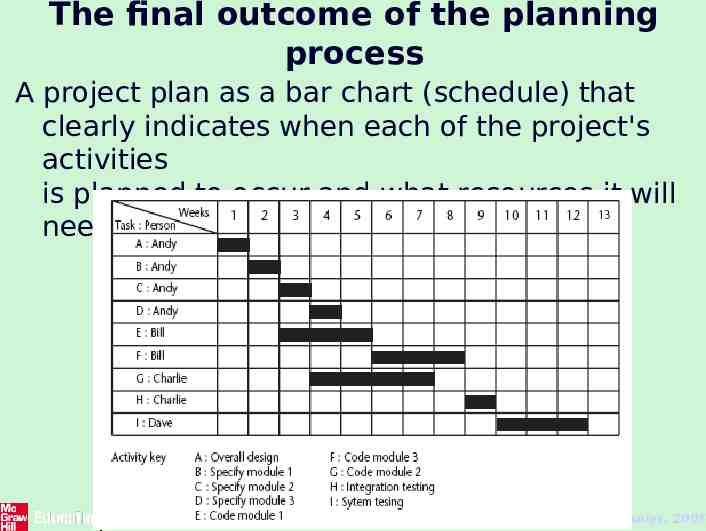
The final outcome of the planning process A project plan as a bar chart (schedule) that clearly indicates when each of the project's activities is planned to occur and what resources it will need. 9 The McGraw-Hill Companies, 2005

Network Planning Models These project scheduling techniques model the project's activities and their relationships as a network. In the network, time flows from left to right the two best known being CPM (Critical Path Method) and PERT (Program Evaluation Review Technique). 10 The McGraw-Hill Companies, 2005

Formulating a Network Model The first stage in creating a network model is to represent the activities and their interrelationships as a graph. In activity-on-node we do this by representing activities as nodes (boxes) in the graph - the lines between nodes represent dependencies. an activity-on-arrow approach to visualizing the project as a network where activities are drawn as arrows joining circles, or nodes, which represent the possible start and/or completion of an activity or set of activities 11 The McGraw-Hill Companies, 2005

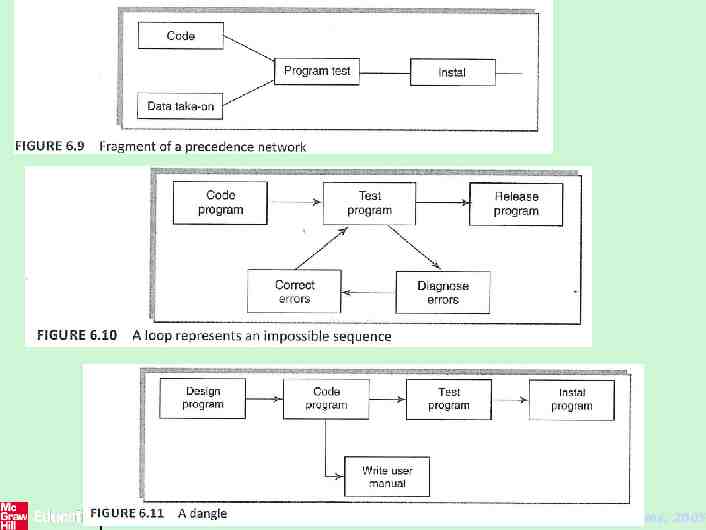
Constructing precedence networks Rules for networks construction 1. project network should have only one start node 2. A project network should have only one end node 3. Node has duration: A node represents an activity and, in general, activities take time to execute 4. Links normally have no duration: Links represent the relationships between activities. In Figure 6.9 installation cannot start until program testing is complete. 5. Precedents are the immediate preceding activities : In Figure 6.9, the activity 'Program test' cannot start until both 'Code' and 'Data take-on' have been completed and activity 'Install' cannot start until 'Program test' has finished. 12 The McGraw-Hill Companies, 2005

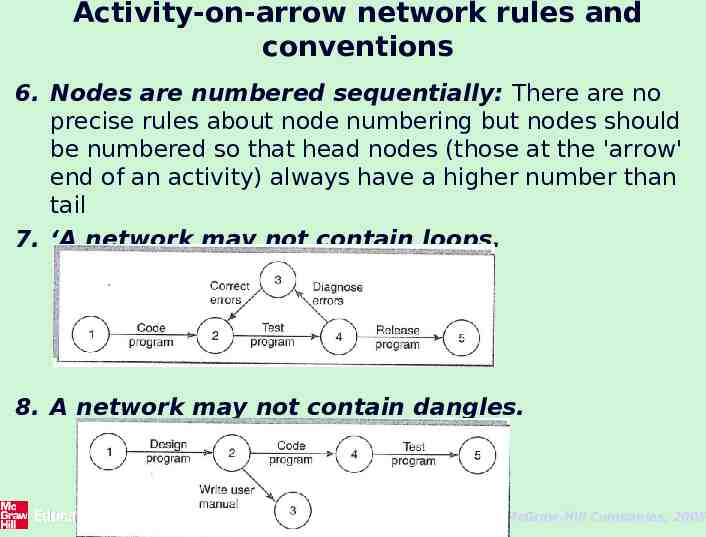
Rules for networks construction(cont.) 6. Time moves from left to right: If at all possible, networks are drawn so that time moves from left to right. 7. A network may not contain loops: Figure 6.10 demonstrates a loop in a network. A loop is an error in that it represents a situation that cannot occur in practice. 8. A network should not contain dangles: A dangling activity such as 'Write user manual' in Figure 6.11 should not exist as it is likely to lead to errors in subsequent analysis. 13 The McGraw-Hill Companies, 2005

14 The McGraw-Hill Companies, 2005

Lagged activities Where there is a fixed delay between activities e.g. seven days notice has to be given to users that a new release has been signed off and is to be installed Acceptance testing 7days Install new release 1day 20 days 15 The McGraw-Hill Companies, 2005

Lagged activities Where activities can occur in parallel with a time lag between them, we represent the lag with a duration on the linking arrow as shown in Figure 6.13. This indicates that documenting amendments can start one day after the start of prototype testing and will be completed two days after prototype testing is completed 16 The McGraw-Hill Companies, 2005

Types of links between activities Finish to start Software development Acceptance testing Start to start/ Finish to finish Test prototype 2 days 1 day Document Amendments 17 The McGraw-Hill Companies, 2005

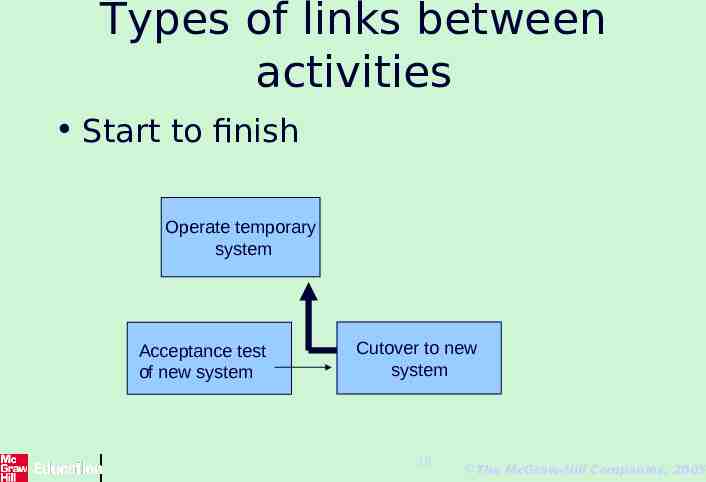
Types of links between activities Start to finish Operate temporary system Acceptance test of new system Cutover to new system 18 The McGraw-Hill Companies, 2005

Start and finish times Latest finish Earliest start activity Earliest finish Latest start Activity ‘write report software’ Earliest start (ES) Earliest finish (EF) ES duration Latest finish (LF) latest task can be completed without affecting project end Latest start LF - duration 19 The McGraw-Hill Companies, 2005

Example earliest start day 5 latest finish day 30 duration 10 days earliest finish ? latest start ? 20 The McGraw-Hill Companies, 2005

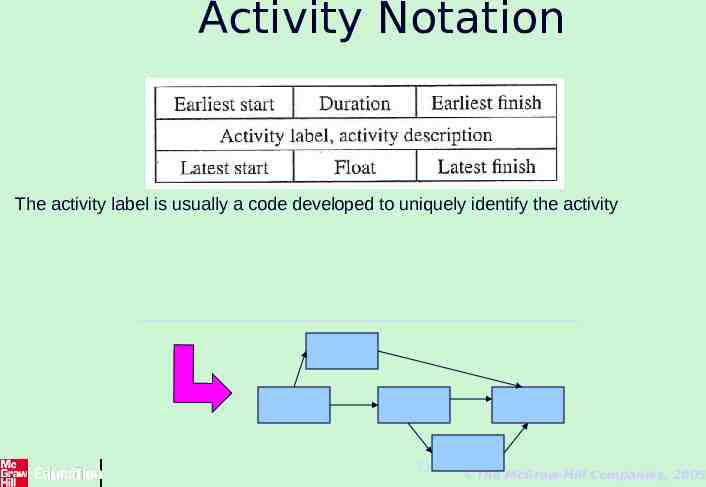
Activity Notation The activity label is usually a code developed to uniquely identify the activity 21 The McGraw-Hill Companies, 2005

Earliest start date Earliest start date for the current activity earliest finish date for the previous When there is more than one previous activity, take the latest earliest finish Note ‘day 7’ end of work on day 7 EF day 7 ES day10 EF day10 22 The McGraw-Hill Companies, 2005

Adding the Time Dimension The critical path approach is concerned with two primary objectives: planning the project in such a way that it is completed as quickly as possible; and identifying those activities where a delay in their execution is likely to affect the overall end date of the project or later activities' start dates. The method requires that for each activity we have an estimate of its duration. The network is then analyzed by carrying out a forward pass, to calculate the earliest dates at which activities may commence and the project be completed, and a backward pass, to calculate the latest start dates for activities and the critical path. 23 The McGraw-Hill Companies, 2005

Exercise Draw activity network using precedence network convention for the project specified in table 6.1 24 The McGraw-Hill Companies, 2005

Where an actual start date is known, the calculations may be carried out using actual dates. Alternatively we can use day or week numbers 25 The McGraw-Hill Companies, 2005

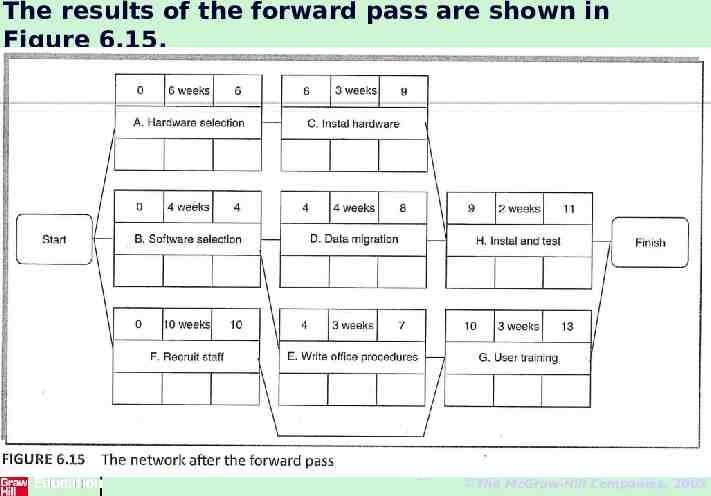
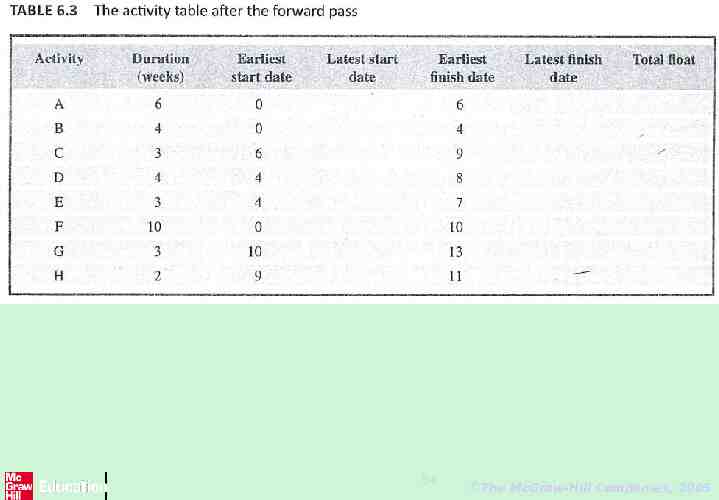
The forward pass The forward pass is carried out to calculate the earliest dates on which each activity may be started and completed. The forward pass and the calculation of earliest start dates for precedence network in fig 6.14 : 1. Activities A, B and F may start immediately, so the earliest date for their start is zero. 2. Activity A will take 6 weeks, so the earliest it can finish is week 6. 3. Activity B will take 4 weeks, so the earliest it can finish is week 4. 4. Activity F will take 10 weeks, so the earliest it can finish is week 10. 5. Activity C can start as soon as A has finished so its earliest start date is week 6. It will take 3 weeks so the earliest it can finish is week 9. 26 The McGraw-Hill Companies, 2005

6. Activities D and E can start as soon as B is complete so the earliest they can each start is week 4. Activity D, which will take 4 weeks, can therefore finish by week 8 and activity E, which will take 3 weeks, can therefore finish by week 7. 7. Activity G cannot start until both E and F have been completed. It cannot therefore start until week 10 – the later of weeks 7 (for activity E) and 10 (for activity F). It takes 3 weeks and finishes in week 13. 8. Similarly, Activity H cannot start until week 9 – the later of the two earliest finish dates for the preceding activities C and D. 9. The project will be complete when both activities Hand G have been completed. Thus the earliest project completion date will be the later of weeks 11 and 13 - that is, week 13. 27 The McGraw-Hill Companies, 2005

The results of the forward pass are shown in Figure 6.15. 28 The McGraw-Hill Companies, 2005

The Backward Pass The second stage in the analysis of a critical path network is to carry out a backward pass to calculate the latest date at which each activity may be started and finished without delaying the end date of the project. In calculating the latest dates, we assume that the latest finish date for the project is the same as the earliest finish date - that is, we wish to complete the project as early as possible 29 The McGraw-Hill Companies, 2005

The Backward Pass Figure 6.16 illustrates our network after carrying out the backward pass. The latest activity dates are calculated as follows. 1. The latest completion date for activities G and H is assumed to be week 13. 2. Activity H must therefore start at week 11 at the latest (13 2) and the latest start date for activity G is week 10 (13 - 3). 3. The latest completion date for activities C and D is the latest date at which activity H must start - that is, week 11. They therefore have latest start dates of week 8 (11 - 3) and week 7 (11 - 4) respectively. 30 The McGraw-Hill Companies, 2005

4. Activities E and F must be completed by week 10 so their earliest start dates are weeks 7 (10 - 3) and 0(10 - 10) respectively. 5. Activity B must be completed by week 7 (the latest start date for both activities D and E) so its latest start is week 3 (7 - 4). 6. Activity A must be completed by week 8 (the latest start date for activity C) so its latest start is week 2 (8 - 6). The latest start date for the project start is the earliest of the latest start dates for activities A, B and F. This is week zero. This is, of course, not very surprising since it tells us that if the project does not start on time it won't finish on time. 31 The McGraw-Hill Companies, 2005

The results of the backward pass are shown in Fig 6.16. 32 The McGraw-Hill Companies, 2005

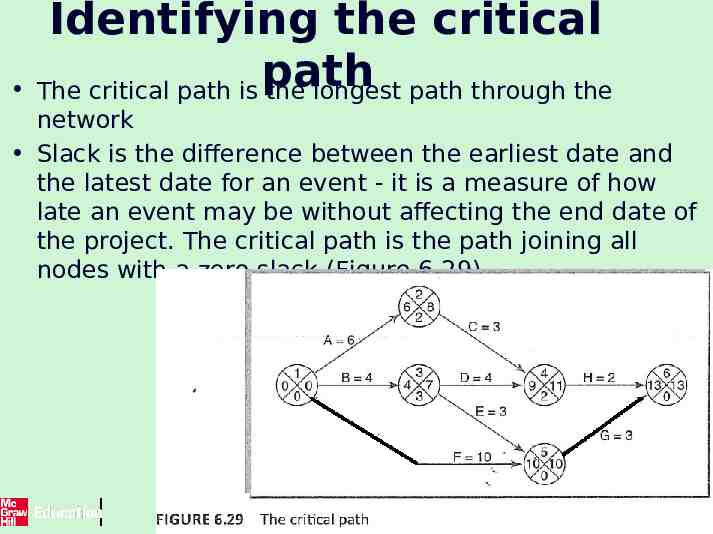
Identifying the Critical Path There will be at least one path through the network (that is, one set of successive activities) that defines the duration of the project. This is known as the critical path. Any delay to any activity on this critical path will delay the completion of the project. The difference between an activity's earliest start date and its latest start date (or, the difference between its earliest‘ and latest finish dates) is known as the activity's float : – it is a measure of how much the start or completion of an activity may be delayed without affecting the end date of the project. 33 The McGraw-Hill Companies, 2005

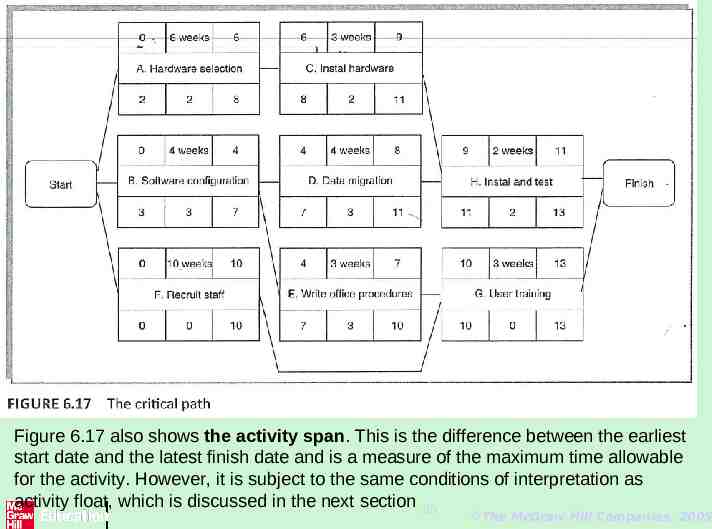
Identifying the Critical Path Any activity with a float of zero is critical in the sense that any delay in carrying out the activity will delay the completion date of the project as a whole. There will always be at least one path through the network joining those critical activities - this path is known as the critical path and is shown bold in Figure 6.17. The significance of the critical path is two-fold. – In managing the project, we must pay particular attention to monitoring activities on the critical path so that the effects of any delay or resource unavailability are detected and corrected at the earliest opportunity. – In planning the project, it is the critical path that we must shorten if we are to reduce the overall duration of the project. 34 The McGraw-Hill Companies, 2005

Figure 6.17 also shows the activity span. This is the difference between the earliest start date and the latest finish date and is a measure of the maximum time allowable for the activity. However, it is subject to the same conditions of interpretation as activity float, which is discussed in the next section 35 The McGraw-Hill Companies, 2005

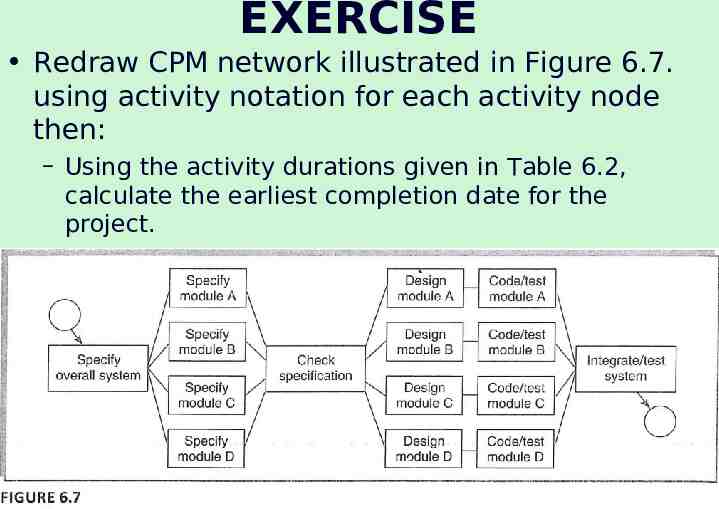
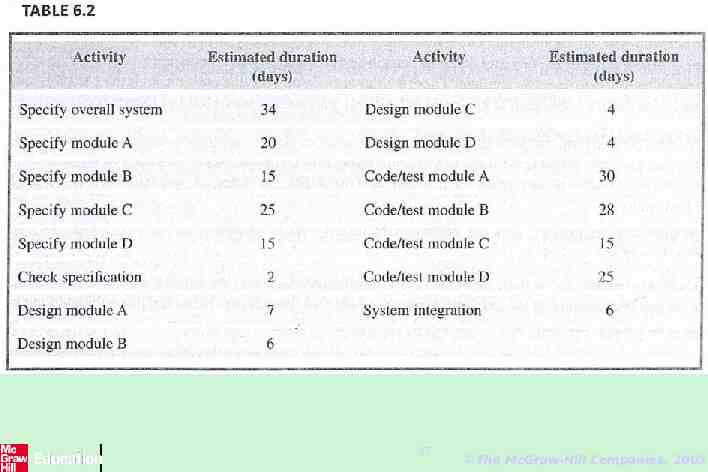
EXERCISE Redraw CPM network illustrated in Figure 6.7. using activity notation for each activity node then: – Using the activity durations given in Table 6.2, calculate the earliest completion date for the project. – identify the critical path on your network 36 The McGraw-Hill Companies, 2005

37 The McGraw-Hill Companies, 2005

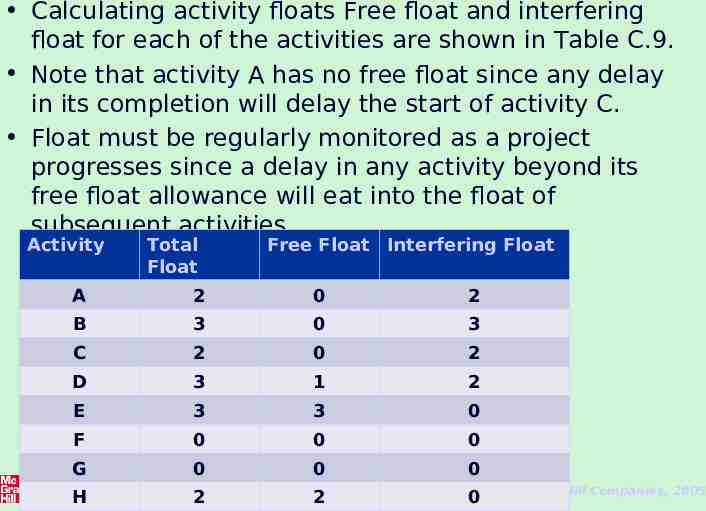
Activity Float Free float: the time by which an activity may be delayed without affecting any subsequent activity. It is calculated as the difference between the earliest completion date for the activity and the earliest start date of the succeeding activity. Interfering float: the difference between total float and free float. – Once the free float has been used (or if it is zero), the interfering float tells us by how much the activity may be delayed without delaying the project end date - even though it will delay the start of subsequent activities. EXERCISE: Calculate the free float and interfering float for each of the activities shown in the activity network (Figure 6.17). 38 The McGraw-Hill Companies, 2005

Calculating activity floats Free float and interfering float for each of the activities are shown in Table C.9. Note that activity A has no free float since any delay in its completion will delay the start of activity C. Float must be regularly monitored as a project progresses since a delay in any activity beyond its free float allowance will eat into the float of subsequent activities. Activity Total Float Free Float Interfering Float A 2 0 2 B 3 0 3 C 2 0 2 D 3 1 2 E 3 3 0 F 0 0 0 G 0 0 H 2 2 39 0 The McGraw-Hill Companies, 2005 0

Shortening the Project Duration To shorten the overall duration of a project reduce activity durations (ex: applying more resources to the task). The critical path indicates where we must look to save time Referring to Figure 6.17, it can be seen that we could complete the project in week 12 by reducing the duration of activity F by one week (to 9 weeks). As we reduce activity times along the critical path we must continually check for any new critical path emerging and redirect our attention where necessary. 40 The McGraw-Hill Companies, 2005

Shortening the Project Duration There will come a point when we can no longer safely, or costeffectively, reduce critical activity durations in an attempt to bring forward the project end date. Generally, time savings are to be found by increasing the amount of parallelism in the network and the removal of bottlenecks EXERCISE: Referring to Figure 6.17, suppose that the duration for activity F is shortened to 8 weeks. – Calculate the end date of the project – What would the end date for the project be if activity F were shortened to 7 weeks? Why? 41 The McGraw-Hill Companies, 2005

Shortening activity F to 8 weeks will bring the project completion date forward to week 11 – that is, it will save 2 weeks on the duration of the project. However, there are now two critical paths, startF-G-finish and start-A-C-H-finish, so that reducing the duration of activity F any further will not shorten the project duration any further. If we wish to complete the project earlier than week 11 we must save time on both of these critical paths. 42 The McGraw-Hill Companies, 2005

Identifying Critical Activities The critical path identifies those activities which are critical to the end date of the project; However, activities that are not on the critical path may become critical. As the project proceeds, activities will invariably use up some of their float and this will require a periodic recalculation of the network. As soon as the activities along a particular path use up their total float then that path will become a critical path and a number of noncritical activities will suddenly become critical. 43 The McGraw-Hill Companies, 2005

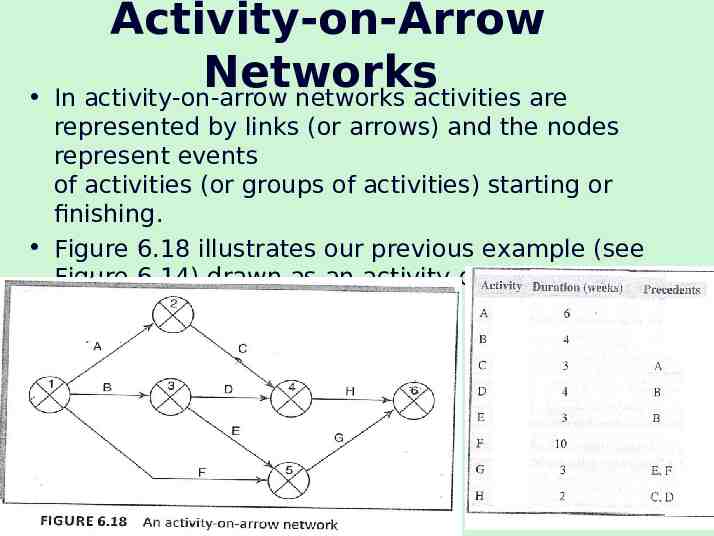
Activity-on-Arrow Networks In activity-on-arrow networks activities are represented by links (or arrows) and the nodes represent events of activities (or groups of activities) starting or finishing. Figure 6.18 illustrates our previous example (see Figure 6.14) drawn as an activity-on-arrow network 44 The McGraw-Hill Companies, 2005

Activity-on-arrow network rules and conventions 1. A project network may have only one start node. 2. A project network may have only one end node. 3. link has duration: link represents activity and, in general, activities take time to execute. 4. Nodes have no duration: Nodes are events and, as such, are instantaneous points in time. – The source node is the event of the project becoming ready to start and the sink node is the event of the project becoming completed. – Intermediate nodes represent two simultaneous events - the event of all activities leading into a node having been completed and the event of all activities leading out of that node being in a position to be started. 5. Time moves from left to right. 45 The McGraw-Hill Companies, 2005

Activity-on-arrow network rules and conventions 6. Nodes are numbered sequentially: There are no precise rules about node numbering but nodes should be numbered so that head nodes (those at the 'arrow' end of an activity) always have a higher number than tail 7. ‘A network may not contain loops. 8. A network may not contain dangles. 46 The McGraw-Hill Companies, 2005

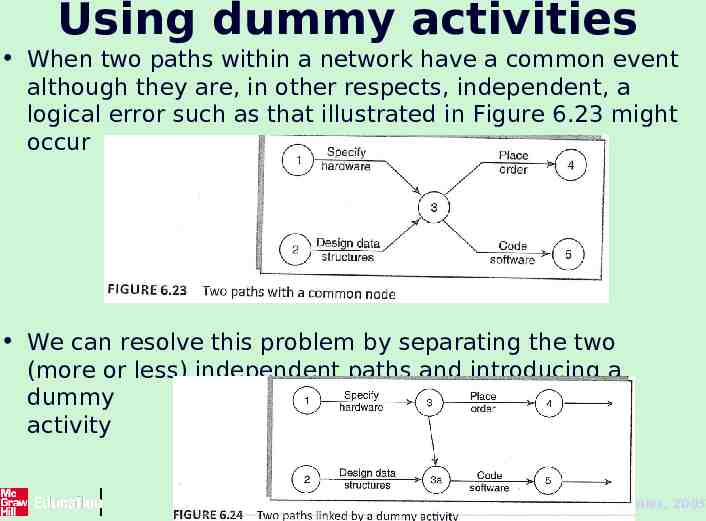
Using dummy activities When two paths within a network have a common event although they are, in other respects, independent, a logical error such as that illustrated in Figure 6.23 might occur We can resolve this problem by separating the two (more or less) independent paths and introducing a dummy activity 47 The McGraw-Hill Companies, 2005

Using dummy activities Dummy activities, shown as dotted lines on the network diagram, have a zero duration and use no resources. They are often used to aid in the layout of network drawings as in Figure 6.25. The use of a dummy activity where two activities share the same start and end nodes makes it easier to distinguish the activity end-points. These are problems that do not occur with activity-onnode networks. 48 The McGraw-Hill Companies, 2005

Representing lagged activities We need to represent these with pairs of dummy activities as shown in Figure 6.26. 49 The McGraw-Hill Companies, 2005

Activity labelling One of the more common conventions for labelling nodes is the following: The latest and earliest dates by which the event should occur, and the event slack (which will be explained later). 50 The McGraw-Hill Companies, 2005

The forward pass (activity-onarrow network.) The forward pass is carried out to calculate the earliest date on which each event may be achieved and the earliest dates on which each activity may be started and completed. The earliest date for an event is the earliest date by which all activities upon which it depends can be completed. Using Figure 6.18 and Table 6.1 the calculation proceeds according to the following reasoning: Activities A, Band F may start immediately, so the earliest date for event 1 is zero and the earliest start date for these three activities is also zero. Activity A will take 6 weeks, so the earliest it can finish is week 6 (recorded in the activity table). Therefore the earliest we can achieve event 2 is week 6. 51 The McGraw-Hill Companies, 2005

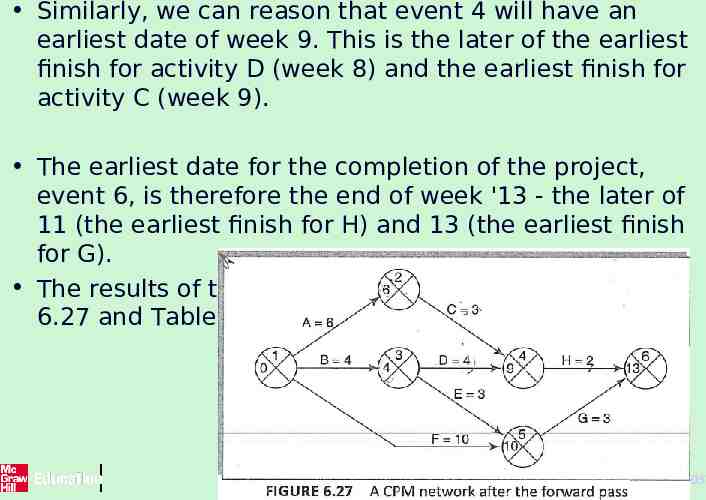
Activity B will take 4 weeks, so the earliest it can finish and the earliest we can achieve event 3 is week 4. Activity F will take 10 weeks, so the earliest it can finish is week 10- we cannot, however, tell whether or not this is also the earliest date that we can achieve event 5 since we have not, as yet, calculated when activity E will finish. Activity E can start as early as week 4 (the earliest date for event 3) and, since it is forecasted to take 3 weeks, will be completed, at the earliest, at the end of week 7. Event 5 may be achieved when both E and F have been completed, that is, week 10 (the later of 7 and 10). 52 The McGraw-Hill Companies, 2005

Similarly, we can reason that event 4 will have an earliest date of week 9. This is the later of the earliest finish for activity D (week 8) and the earliest finish for activity C (week 9). The earliest date for the completion of the project, event 6, is therefore the end of week '13 - the later of 11 (the earliest finish for H) and 13 (the earliest finish for G). The results of the forward pass are shown in Figure 6.27 and Table 6.3. 53 The McGraw-Hill Companies, 2005

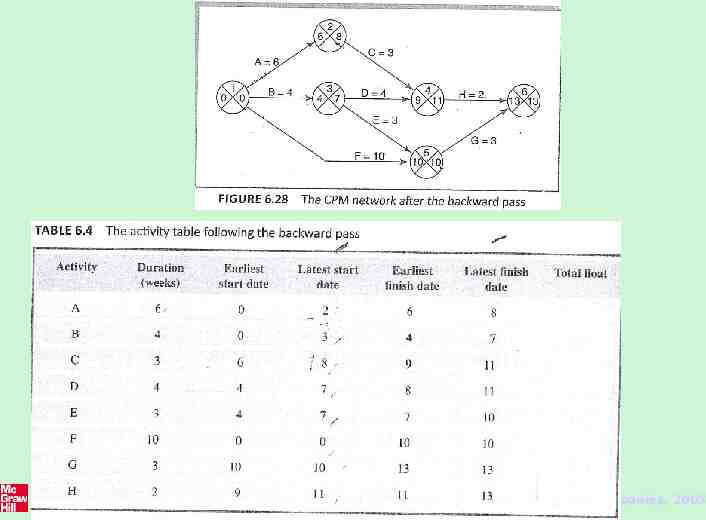
54 The McGraw-Hill Companies, 2005

The backward pass (activity-onarrow network.) The second stage is to carry out a backward pass to calculate the latest date at which each event may be achieved, and each activity started and finished, without delaying the end date of the project. The latest date for an event is the latest date by which all immediately following activities must be started for the project to be completed on time. we assume that the latest finish date for the project is the same as the earliest finish date - that is, we wish to complete the project as early as possible. Figure 6.28 illustrates our network and Table 6.4 the activity table after carrying out the backward pass - as with the forward pass, event dates are recorded on the diagram and activity dates on the activity table . 55 The McGraw-Hill Companies, 2005

56 The McGraw-Hill Companies, 2005

Identifying the critical The critical path is path the longest path through the network Slack is the difference between the earliest date and the latest date for an event - it is a measure of how late an event may be without affecting the end date of the project. The critical path is the path joining all nodes with a zero slack (Figure 6.29). 57 The McGraw-Hill Companies, 2005

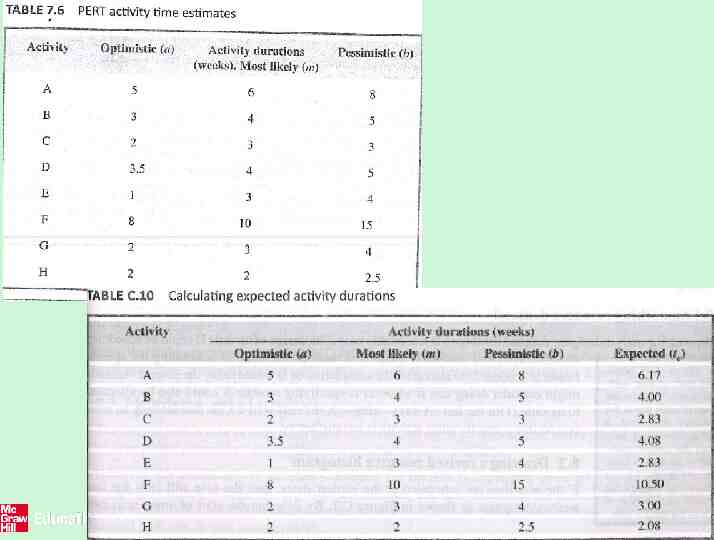
PERT Technique PERT was developed to take account of the uncertainty surrounding estimates of task durations. The method is very similar to the CPM technique but, instead of using a single estimate for the duration of each task, PERT requires three estimates: – Most likely time – Optimistic time – Pessimistic time 58 The McGraw-Hill Companies, 2005

PERT Technique Most likely time (m): the time we would expect the task to take under normal circumstances. Optimistic time (a): the shortest time in which we could expect to complete the activity. Pessimistic time (b): the worst possible time. PERT then combines these three estimates to form a single expected duration, te using the formula The McGraw-Hill Companies, 2005

EXERCISE Table 7.6 provides additional activity duration estimates for the network shown in Figure 6.29. There are new estimates for a and b and the original activity duration estimates have been used as the most likely times, m. Calculate the expected duration, te for each activity. 60 The McGraw-Hill Companies, 2005

61 The McGraw-Hill Companies, 2005

Using expected durations The expected durations are used to carry out a forward pass through a network, using the same method as the CPM technique. In this case, however, the calculated event dates are not the earliest possible dates but the dates by which we expect to achieve those events. 62 The McGraw-Hill Companies, 2005

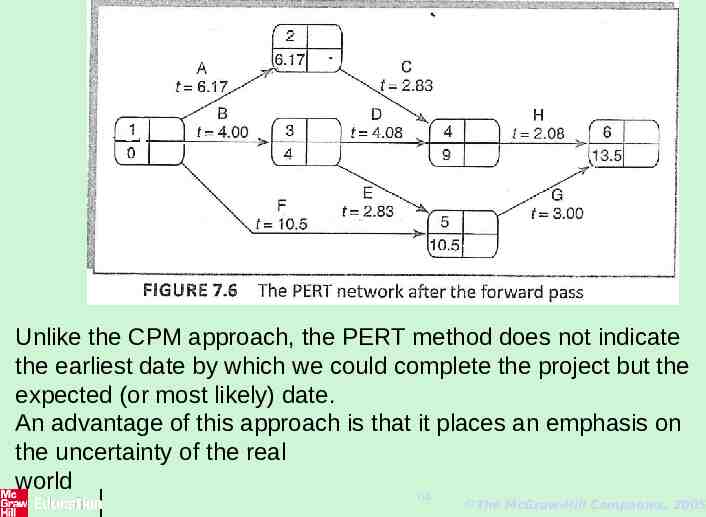
EXERCISE Use your calculated expected activity durations in previous exercise to carry out a forward pass through the network (Figure 6.29) and verify that the project duration is 13.5 weeks. The PERT network illustrated in Figure 7.6 indicates that we expect the project to take 13.5 weeks. In Figure 7.6 we have used an activity-on-arrow, of course, be equally well supported by activity-on-node diagrams 63 The McGraw-Hill Companies, 2005

Unlike the CPM approach, the PERT method does not indicate the earliest date by which we could complete the project but the expected (or most likely) date. An advantage of this approach is that it places an emphasis on the uncertainty of the real world 64 The McGraw-Hill Companies, 2005

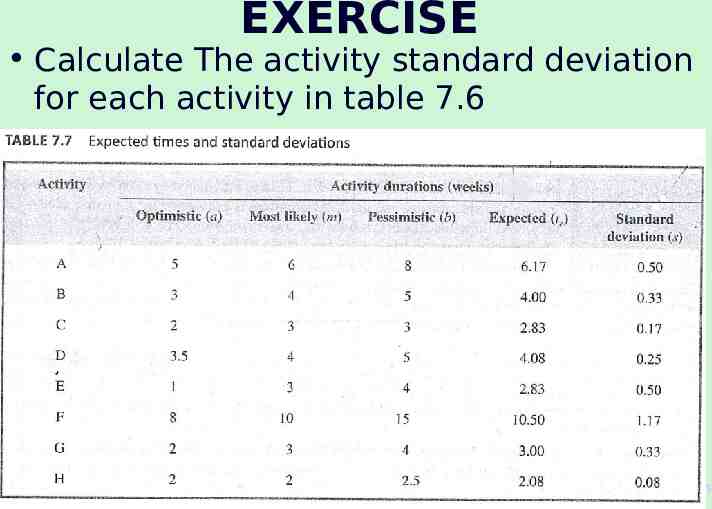
Activity standard deviations A quantitative measure of the degree of uncertainty of an activity duration estimate may be obtained by calculating the standard deviation s of an activity time, using the formula 65 The McGraw-Hill Companies, 2005

EXERCISE Calculate The activity standard deviation for each activity in table 7.6 66 The McGraw-Hill Companies, 2005

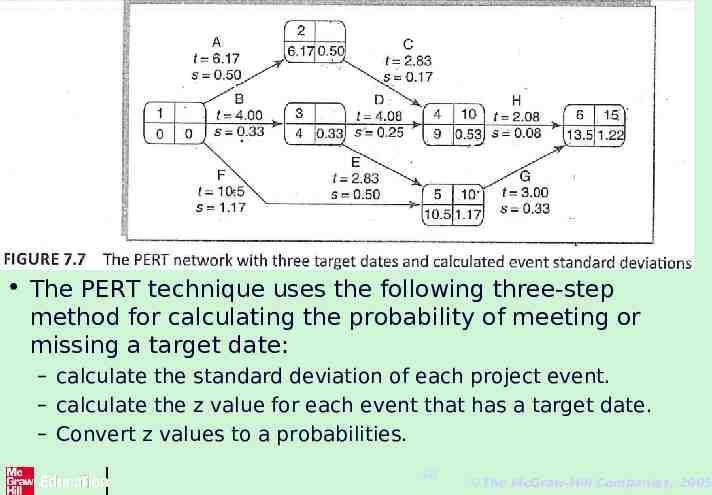
The likelihood of meeting The main advantage of targets the PERT technique is that it provides a method for estimating the probability of meeting or missing target dates. – Suppose that we must complete the project within 15 weeks at the outside. – We expect it will take 13.5 weeks but it could take more or, perhaps, less. – In addition, Suppose that activity C must be completed by week 10, as it is to be carried out by a member of staff who is scheduled to be working on another project, and that event 5 represents the delivery of intermediate products to the customer, which must take place by week 10. – These three target dates are shown on the PERT network in Figure 7.7. 67 The McGraw-Hill Companies, 2005

The PERT technique uses the following three-step method for calculating the probability of meeting or missing a target date: – calculate the standard deviation of each project event. – calculate the z value for each event that has a target date. – Convert z values to a probabilities. 68 The McGraw-Hill Companies, 2005

Calculating the standard deviation of each project event Standard deviations for the project events can be calculated by carrying out a forward pass using the activity standard deviations in a manner similar to that used with expected durations. There is, however, one small difference - to add two standard deviations we must add their squares and then find the square root of the sum. 69 The McGraw-Hill Companies, 2005

EXERCISE The McGraw-Hill Companies, 2005

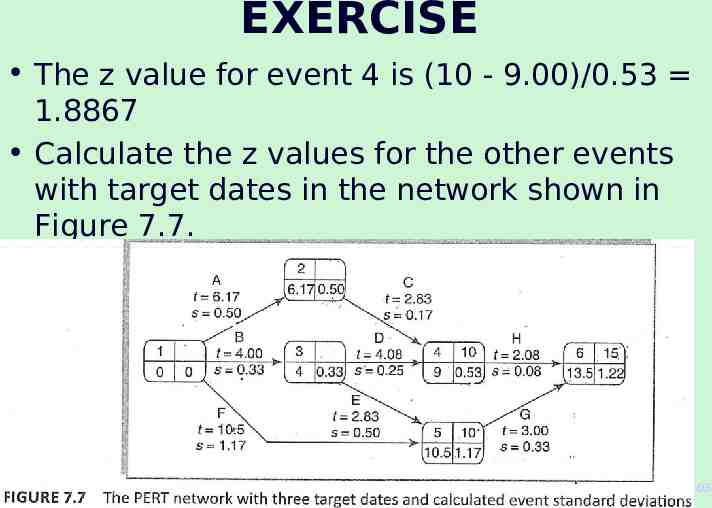
Calculating the z values The z value is calculated for each node that has a target date. It is equivalent to the number of standard deviations between the node's expected and target dates. It is calculated using the formula: where te is the expected date and T is the target date. 71 The McGraw-Hill Companies, 2005

EXERCISE The z value for event 4 is (10 - 9.00)/0.53 1.8867 Calculate the z values for the other events with target dates in the network shown in Figure 7.7. 72 The McGraw-Hill Companies, 2005

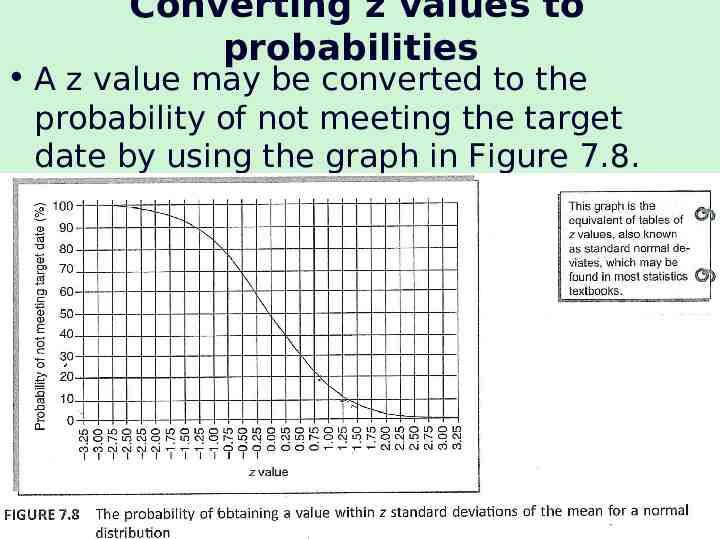
Converting z values to probabilities A z value may be converted to the probability of not meeting the target date by using the graph in Figure 7.8. 73 The McGraw-Hill Companies, 2005

EXERCISE The z value for the project completion (event 6) is 1.23. Using Figure 7.8 we can see that this equates to a probability of approximately 11 %, that is, there is an 11 % risk of not meeting the target date of the end of week15 Find the probabilities of not achieving events 4 or 5 by their target dates of the end of week 10. What is the likelihood of completing the project by week 14? 74 The McGraw-Hill Companies, 2005

Event 4: The z value is 1.89 which equates to a probability of approximately 3%. There is therefore only a 3% chance that we will not achieve this event by the target date of the end of week 10. Event 5: The z value is -0.43 which equates to a probability of approximately 67%. There is therefore a 67% chance that we will not achieve this event by the target date of the end of week 10. To calculate the probability of completing the project by week 14 we need to calculate a new z value for event 6 using a target date of 14. This new z value is : (14-13.5)/1.22 0.41. This equates to a probability of approximately 35%. This is the probability of not meeting the target date. The probability of meeting the target date is therefore 65% (100% - 35%). 75 The McGraw-Hill Companies, 2005

The advantages of We have seen that byPERT requesting multivalued activity duration estimates and calculating expected dates, PERT focuses attention on the uncertainty of forecasting. We can use the technique to calculate the standard deviation for each task and use this to rank them according to their degree of risk. Using this ranking, we can see, for example, that activity F is the one regarding which we have greatest uncertainty, whereas activity C should, in principle, give us relatively little cause for concern. 76 The McGraw-Hill Companies, 2005

The advantages of PERT If we use the expected times and standard deviations for forward passes through the network we can, for any event or activity completion, estimate the probability of meeting any set target. In particular, by setting target dates along the critical path, we can focus on those activities posing the greatest risk to the project's schedule. 77 The McGraw-Hill Companies, 2005