SMT and its Application in Software Verification Chao Wang NEC Labs,

SMT and its Application in Software Verification Chao Wang NEC Labs, Princeton, NJ COS 598d 3/5/2010 1

What is SMT? Satisfiability Modulo Theories (SMT) Decision problem for logic formulas expressed in classical firstorder logic with equality, with respect to combinations of some background theories It is a generalization of SAT, where some Boolean variables are replaced by predicates from a variety of underlying theories. 2

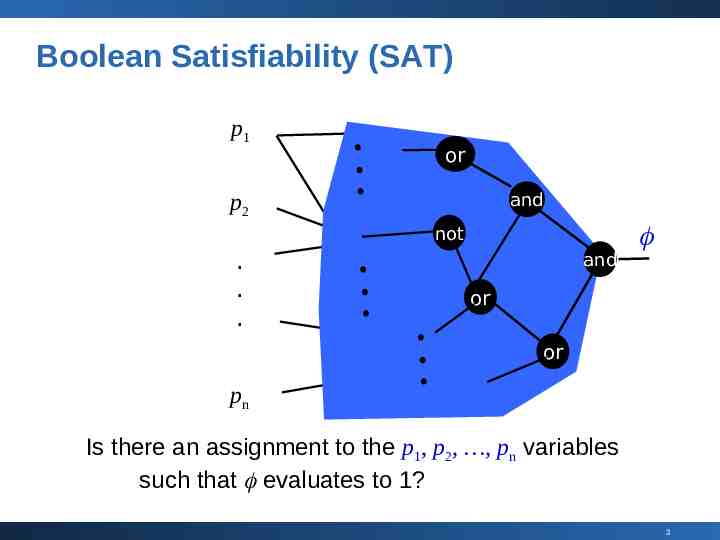
Boolean Satisfiability (SAT) p1 or p2 and not . . . and or or pn Is there an assignment to the p1, p2, , pn variables such that evaluates to 1? 3

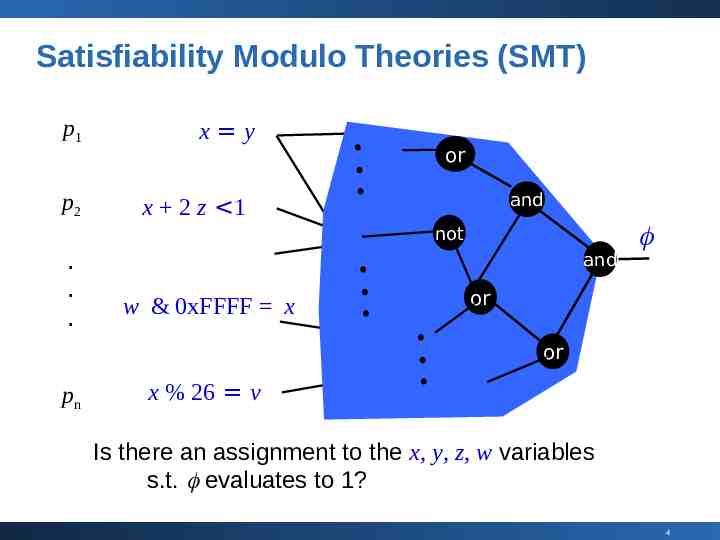
Satisfiability Modulo Theories (SMT) p1 p2 x y or and x 2 z 1 not . . . and w & 0xFFFF x or or pn x % 26 v Is there an assignment to the x, y, z, w variables s.t. evaluates to 1? 4

SMT Solvers: A Brief History Early work in the late 1970s Nelson and Oppen, Shostak, Boyer and Moore Modern SMT solvers started in the late 1990s Attempts to build scalable solvers Influenced by SAT solvers (GRASP and Chaff) Last few years: tremendous progress Efficient SMT solvers (SMT-LIB benchmarks, SMT-COMP solver competition) Wide-spread applications 5

Many of its Applications Verification systems HOL, Isabelle, and PVS, etc. ACL2, Caduceus, SAL, UCLID, etc. Extended static checkers and model checkers Boogie, ESC/Java 2, etc. BLAST, Eureka, MAGIC, SLAM, F-Soft, etc. Certifying compliers Touchstone, TVOC, etc. Test case generation DART, EXE, CUTE, PEX, etc. 6

Outline What’s SMT? Some Useful Theories Inside SMT Solvers How to Use It? Application in Software Verification 7

First-Order Logic (quantifier-free) Logical Symbols Propositional connectives: AND, OR, NEGATION,etc. Boolean variables: v1, v2, . . . Non-logical symbols/Parameters Equality: Functions: , -, %, bit-wise &, f(), concat, Predicates: ·, is substring, Constant symbols: 0, 1.0, null, 8

Some Useful Theories QF UF: Theory of equality (with uninterpreted functions) QF LIA, QF LIR: Theories of linear arithmetic (over Q or Z) QF IDL, QF RDL: Theories of difference logic (over Q or Z) QF BV: Theories of fixed-size bit-vectors QF A, QF AX: Theory of arrays (with and w/o extensionality) Misc.: Non-linear arithmetic, 9

Example: QF UF Formula (x y) & (y z) & (f(x) f(z)) Transitivity: (x y) & (y z) (x z) Congruence: (x z) (f(x) f(z)) 10

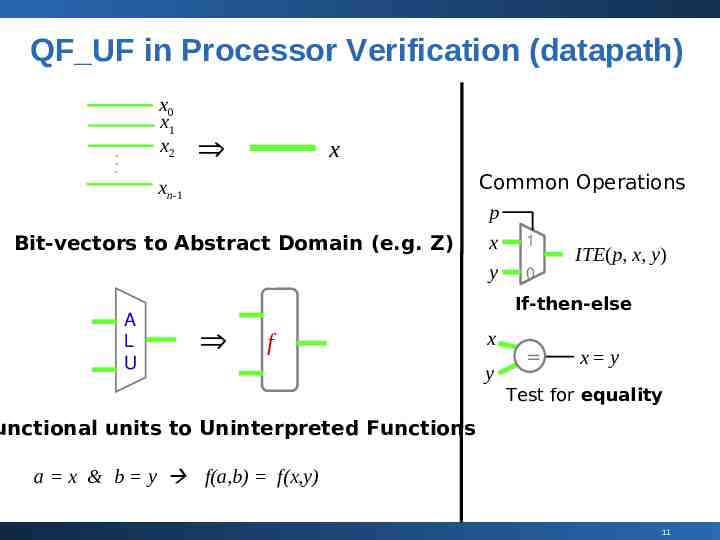
QF UF in Processor Verification (datapath) x0 x1 x2 x xn-1 Bit-vectors to Abstract Domain (e.g. Z) A L U Common Operations p x 1 ITE(p, x, y) y 0 If-then-else f x y x y Test for equality unctional units to Uninterpreted Functions a x & b y f(a,b) f(x,y) 11

QF UF in Equivalence Checking int fun1(int y) { int x, z; z y; y x; x z; return x*x; } int fun2(int y) { return y*y; } SMT formula Satisfiable not equivalent ( z y & y1 x & x1 z & ret1 x1*x1) & ( ret2 y*y ) & ( ret1 ret2 ) Using SAT to check equivalence (w/ Minisat) 32 bits for y: Did not finish in over 5 hours 16 bits for y: 37 sec. 8 bits for y: 0.5 sec. Using EUF solver: 0.01 sec. By Sanjit Seshia, UC Berkeley 12

Bit-Vector Arithmetic (QF BV) Fixed width data words Arithmetic operations E.g., add/subtract/multiply/divide & comparisons Two’s complement and unsigned operations Bit-wise logical operations Can model int, short, long, etc. E.g., and/or/xor, shift/extract and equality Boolean connectives (define b1::(bitvector 32)) (define b2::(bitvector 32)) (assert (and ( (bv-add b1 (mk-bv 32 1)) b2) (/ (bv-add (mk-bv 32 0) (bv-add (mk-bv 32 1) b1)) b2))) (check) 13

Linear Arithmetic (QF LRA, QF LIA) Boolean combination of linear constraints (a1 x1 a2 x2 an xn b) where xi’s could be in Q or Z Many applications, including: Verification of analog circuits Software verification, e.g., of array bounds 14

Difference Logic (QF IDL, QF RDL) Boolean combination of linear constraints xi – xj cij where xi, xj, cij, are in Q or Z Applications: Software verification (most linear constraints are of this form) Processor data-path verification Job shop scheduling 15

Theory of Arrays (QF AX) Two interpreted functions: select and store select(A,i) store(A,i,d) Read from array A at index i Write d to array A at index i Two main axioms: select( store(A,i,d), I ) d select( store(A,i,d), j ) select(A,j) for i j Extentionality axiom: (forall index i. select(A,i) select(B,i)) (A B) 16

Example: QF AX in Equivalence Checking int fun1(int y) { int x[2]; x[0] y; y x[1]; x[1] x[0]; return x[1]*x[1]; } int fun2(int y) { return y*y; } C. Barrett & S. A. Seshia SMT formula x1 store( x,0,y ) & y1 select( x1,1 ) & x2 store( x1,1,select(x1,0) ) & ret1 sq( select(x2,1) ) & ret2 sq(y) & ( ret1 ret2 ) 17

Outline What’s SMT? Some Useful Theories Inside SMT Solvers How to Use It? Application in Software Verification 18

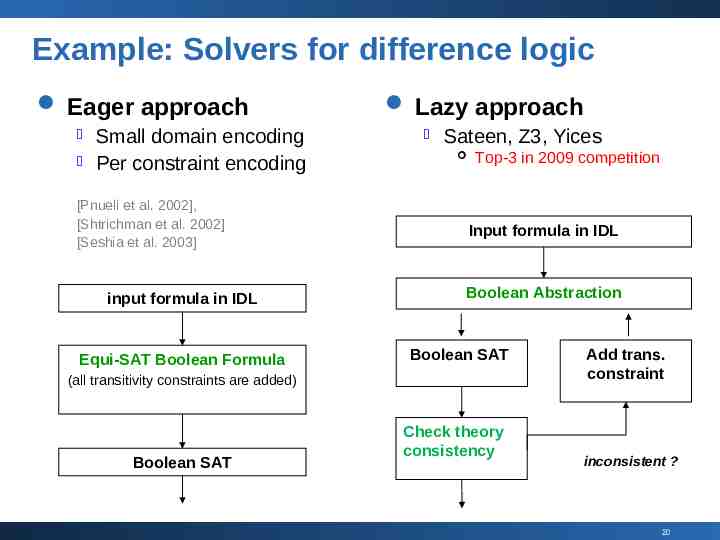
SMT Solvers: “Eager” vs. “Lazy” Eager approach: Translating input formula into an “equisatisfable” Boolean formula using enough consequences of the underlying theory Lazy approach: Writing a dedicated “theory solver” for conjunction of literals in the underlying theory, embedded as a submodule into a Boolean SAT solver 19

Example: Solvers for difference logic Eager approach Small domain encoding Per constraint encoding [Pnueli et al. 2002], [Shtrichman et al. 2002] [Seshia et al. 2003] input formula in IDL Equi-SAT Boolean Formula Lazy approach Sateen, Z3, Yices Top-3 in 2009 competition Input formula in IDL Boolean Abstraction Boolean SAT (all transitivity constraints are added) Boolean SAT Check theory consistency Add trans. constraint inconsistent ? 20

Integer Difference Logic (IDL) Logic to model systems at the “word-level” Subset of a quantifier-free first-order logic Boolean connectives predicates like (x – y c) Formal verification applications Pipelined processors, timed systems, embedded software e.g., back-end of the UCLID Verifier 21

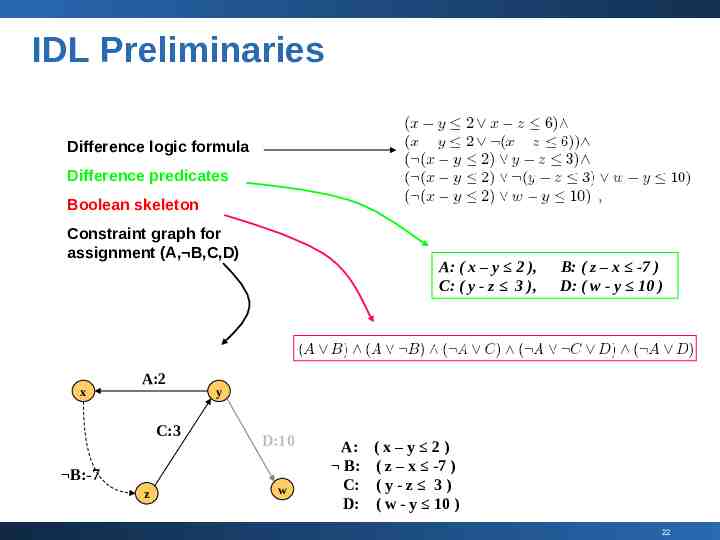
IDL Preliminaries Difference logic formula Difference predicates Boolean skeleton Constraint graph for assignment (A, B,C,D) x A:2 C:3 B:-7 z A: ( x – y 2 ), C: ( y - z 3 ), B: ( z – x -7 ) D: ( w - y 10 ) y D:10 w A: B: C: D: (x–y 2) ( z – x -7 ) (y-z 3) ( w - y 10 ) 22

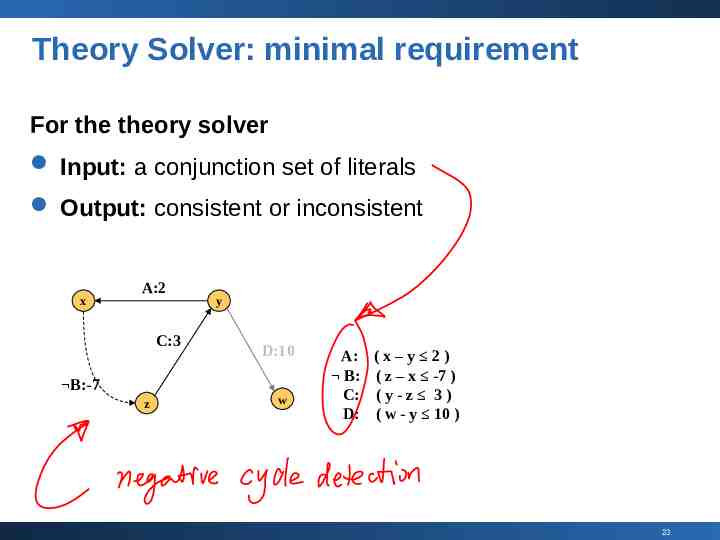
Theory Solver: minimal requirement For the theory solver Input: a conjunction set of literals Output: consistent or inconsistent x A:2 C:3 B:-7 z y D:10 w A: B: C: D: (x–y 2) ( z – x -7 ) (y-z 3) ( w - y 10 ) 23

24

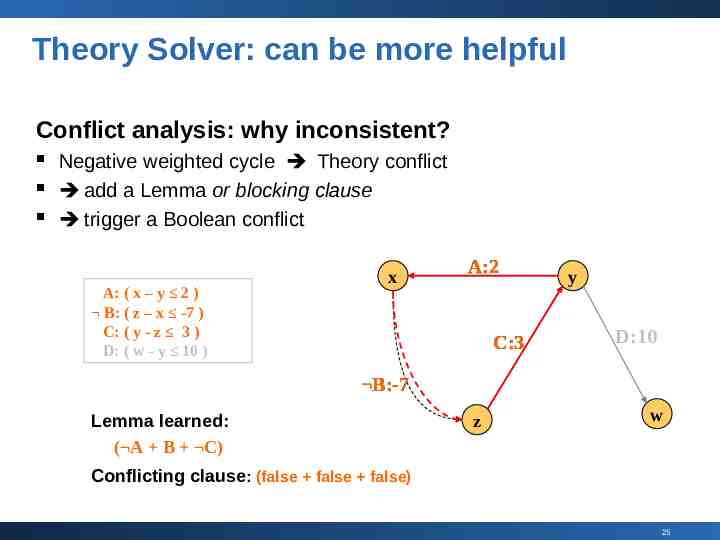
Theory Solver: can be more helpful Conflict analysis: why inconsistent? Negative weighted cycle Theory conflict add a Lemma or blocking clause trigger a Boolean conflict A: ( x – y 2 ) B: ( z – x -7 ) C: ( y - z 3 ) D: ( w - y 10 ) x A:2 C:3 y D:10 B:-7 Lemma learned: ( A B C) z w Conflicting clause: (false false false) 25

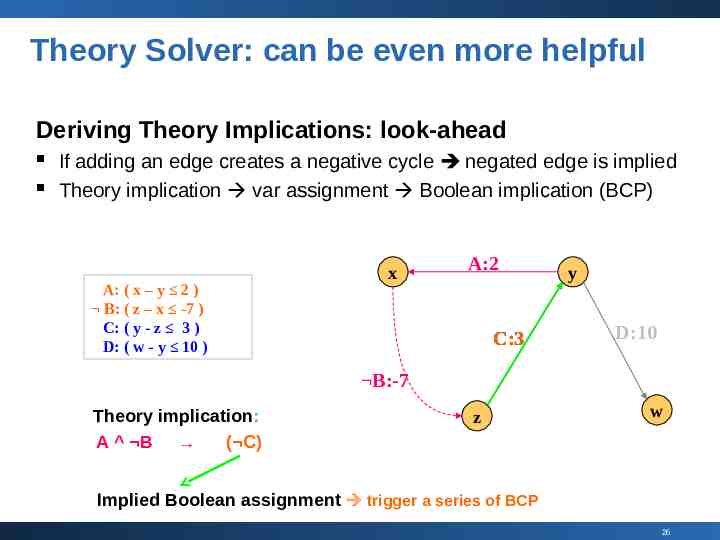
Theory Solver: can be even more helpful Deriving Theory Implications: look-ahead If adding an edge creates a negative cycle negated edge is implied Theory implication var assignment Boolean implication (BCP) A: ( x – y 2 ) B: ( z – x -7 ) C: ( y - z 3 ) D: ( w - y 10 ) x A:2 C:3 y D:10 B:-7 Theory implication: A B ( C) z w Implied Boolean assignment trigger a series of BCP 26

Theory Solver: other desired features Model generation Conflict set generation Deduction of unassigned literals Incremental don’t start from scratch for each call Backtrackable can “undo” steps to a previous state Deduction of interface equalities (eij-deduction) 27

Negative Cycle Detection (standard) Bellman-Ford shortest-paths algorithm Detect negative cycles as by-product Take O(n*m) time sounds good! However, inside SMT Theory solver will be invoked many times, Each time on a very similar sub-problem 28

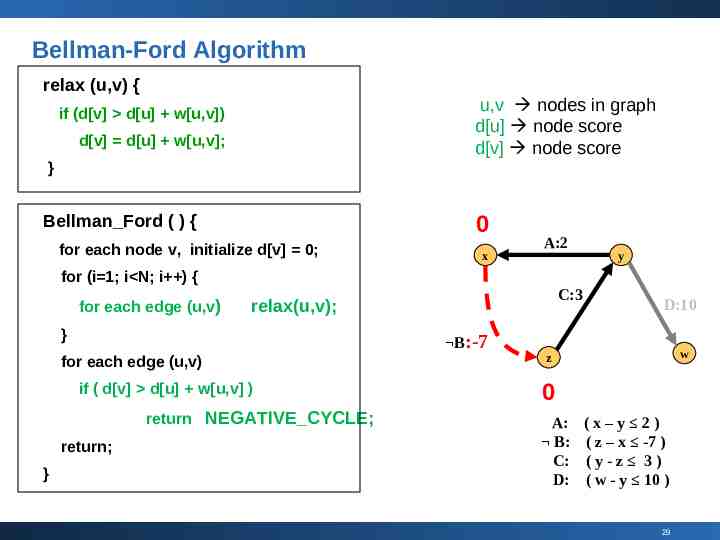
Bellman-Ford Algorithm relax (u,v) { u,v nodes in graph d[u] node score d[v] node score if (d[v] d[u] w[u,v]) d[v] d[u] w[u,v]; } 0 Bellman Ford ( ) { for each node v, initialize d[v] 0; x A:2 y for (i 1; i N; i ) { for each edge (u,v) } for each edge (u,v) if ( d[v] d[u] w[u,v] ) return NEGATIVE CYCLE; return; } C:3 relax(u,v); B:-7 D:10 w z 0 A: B: C: D: (x–y 2) ( z – x -7 ) (y-z 3) ( w - y 10 ) 29

Incremental Algorithm u // after adding the edge (u,v) if ( d[v] d[u] w[u,v] ) { v relax (u,v) enqueue (v) Keep relaxing till it stablize } while ( (x dequeu()) ! null) { for each edge (x,y) { if (d[y] d[x] w[x,y] ) { But before that, if node v is relaxed again, there is a cycle! relax (x,y) if (u x && v y) return NEGATIVE CYCLE; else enqueue (y); }}} return; 30

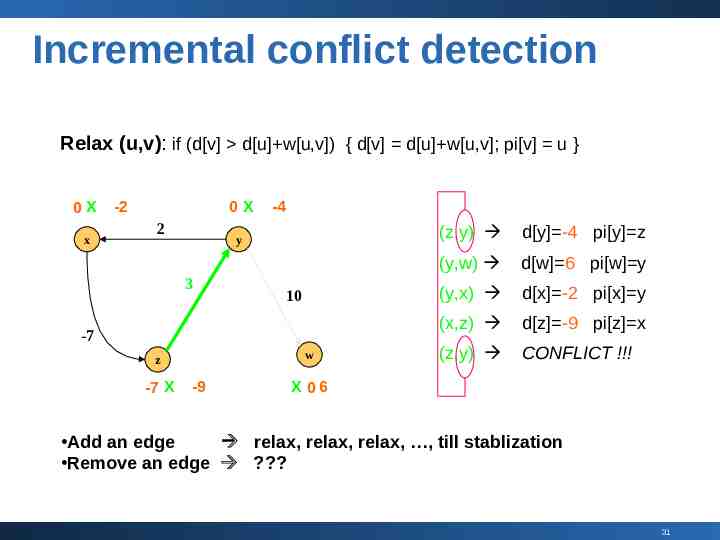
Incremental conflict detection Relax (u,v): if (d[v] d[u] w[u,v]) { d[v] d[u] w[u,v]; pi[v] u } 0X x -2 0X 2 -4 y 3 10 -7 w z -7 X -9 (z,y) d[y] -4 pi[y] z (y,w) d[w] 6 pi[w] y (y,x) d[x] -2 pi[x] y (x,z) d[z] -9 pi[z] x (z,y) CONFLICT !!! X 06 Add an edge relax, relax, relax, , till stablization Remove an edge ? 31

Theory Solver: other desired features Model generation Conflict set generation Deduction of unassigned literals Incremental Backtrackable can “undo” steps to a previous state Deduction of interface equalities (eij-deduction) 32

Fast Backtracking (edge removal) The number of backtracks is very large in practice Should have low runtime overhead can’t start from scratch Should be scalable in terms of memory usage can’t checkpoint Key Observation { d[v] } remains a solution after removing some edges No need to restore the theory solver’s state After the edge removal, nothing needs to be done! Backtracking Cost constant-time!!! 33

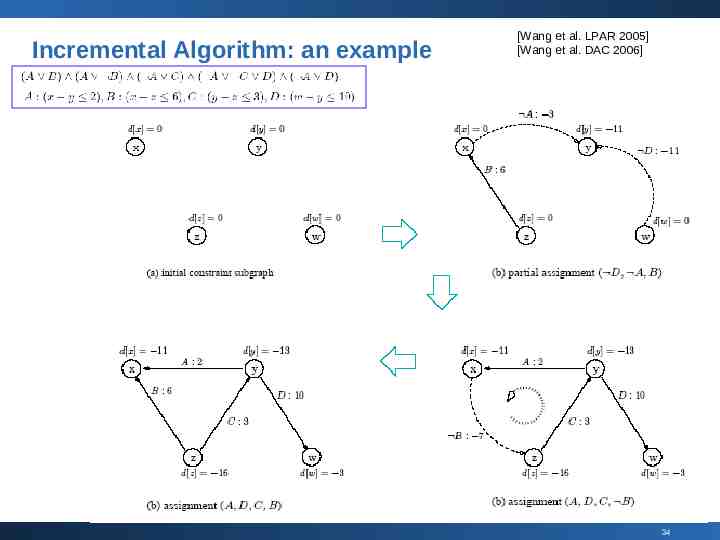
Incremental Algorithm: an example [Wang et al. LPAR 2005] [Wang et al. DAC 2006] 34

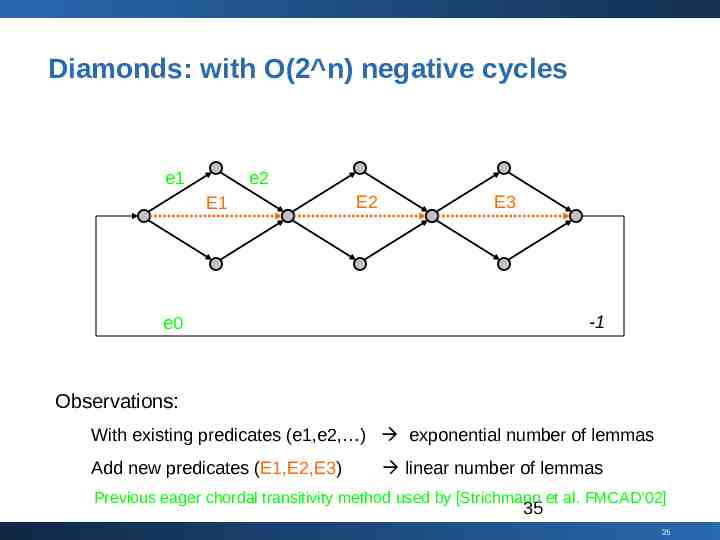
Diamonds: with O(2 n) negative cycles e1 e2 E1 E2 E3 -1 e0 Observations: With existing predicates (e1,e2, ) exponential number of lemmas Add new predicates (E1,E2,E3) linear number of lemmas Previous eager chordal transitivity method used by [Strichmann et al. FMCAD’02] 35 35

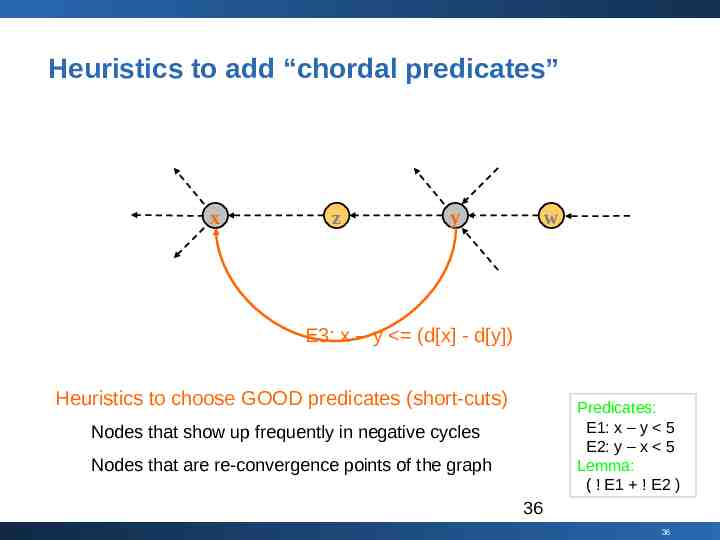
Heuristics to add “chordal predicates” x z y w E3: x – y (d[x] - d[y]) Heuristics to choose GOOD predicates (short-cuts) Predicates: E1: x – y 5 E2: y – x 5 Lemma: ( ! E1 ! E2 ) Nodes that show up frequently in negative cycles Nodes that are re-convergence points of the graph 36 36

Outline What’s SMT? Some Useful Theories Inside SMT Solvers The “lazy” approach The “eager” approach How to Use It? Application in Software Verification 37

Remove Functions: QF UF SAT Ackermann’s Reduction (1954) For each “function symbol occurrence”, add a new variable xf For each pair (xf1, xf2), add “function consistency constraints” Input formula: Output formula: f(a1) & f(a2) & f(a3) xf1 & xf2 & xf3 & (a1 a2) (xf1 xf2) & (a1 a3) (xf1 xf3) & (a2 a3) (xf2 xf3) 38

Remove Functions: QF UF SAT Bryant-German-Velev Reduction (2001) Exploits a property of function applications called “positive equality” Eliminate functions using a nested If-Then-Else expressins Input formula: Output formula: f(a1) & f(a2) & f(a3) xf1 & ITE(a2 a1, xf1, xf2) & ITE(a3 a1, xf1, ITE(a3 a2, xf2, xf3) ) Further Improvement (Lahiri et al. 2004) 39

Small-Domain Encoding: QF LIA SAT For Linear Integer Arithmetic If there is a satisfying solution to a formula, there is one whose size, measured in bits, is polynomially bounded in the problem size With “bounded” integers, one can translate the LIA formula into a pure Boolean formula 40

Small-Domain Encoding: Example Equality constraints of the form (x y), or (x ! y) For a formula with (n) variables, the solution size (d) is bounded by (n). 41

Summary of Solution Bounds Logic Equality logic Difference logic UTVPI logic (Gen2SAT) Full Integer Linear Arithmetic C. Barrett & S. A. Seshia Solution Bound d n n * ( bmax 1 ) 2 * n * ( bmax 1 ) n *(bmax 1) * (amaxk * w k) 42 Tutorial ICCAD 2009 42

Direct Encoding of Theory Axioms Alternative to “small-domain” encoding Also called “per-constraint” encoding For QF UF (equality logic), Bryant and Velev (2001) Cubic – worst-case formula size For QF IDL (difference logic), Strichman et al (2002) Exponential – worst-case formula size For QF LIA (integer arithmetic), Strichman (2002) Double-exponential – worst-case formula size 43

Theory Combination: briefly Problem Statement: Is it possible to combine theory solvers for several component theories, denoted T1, , Tn, into a theory solver that decides ground satisfiability modulo their combination? The answer is negative, in general There are theories with decidable ground satisfiability problems, whose combination is undecidable 44

Theory Combination: briefly Nelson and Oppen (1979,1980): It is possible, if one imposes some restrictions on the component theories and their combination Sufficient conditions (for theories T1 and T2) 1. 2. They are signature-disjoint They are both “stably infinite” 45

Theory Combination: briefly DTC: Delayed Theory Combination (2005, 2006) Rely on DPLL Boolean SAT Little requirement for Theory Solver Eij-Deduction does not need to be complete Delayed Theory Combination vs. Nelson-Oppen for Satisfiability Modulo Theories: a Comparative Analysis, by Bruttomesso et al. in LPAR 2006 46

Outline What’s SMT? Some Useful Theories Inside SMT Solvers How to Use It? Application in Software Verification 47

In Practice: the Yices SMT Solver Features: Producing models, for satisfiable formulas Producing proofs, for unsatisfiable formulas Identifying UNSAT cores subset of the original formula that is also UNSAT Retracting clauses, MAX-SAT, etc. Command-line yices file.ys yices --smt file.smt or // native input format // smt-lib input formula API (programming interface) 48

Outline What’s SMT? Some Useful Theories Inside SMT Solvers How to Use It? Application in Software Verification 49

Symbolic Predictive Analysis for Concurrent Programs Chao Wang NEC Labs, Princeton, NJ Sudipta Kundu UC San Diego Malay Ganai NEC Labs, Princeton, NJ Aarti Gupta NEC Labs, Princeton, NJ Related publications [Wang et al. FM 2009] [Wang et al. FSE 2009] [Wang et al. TACAS2010] 50

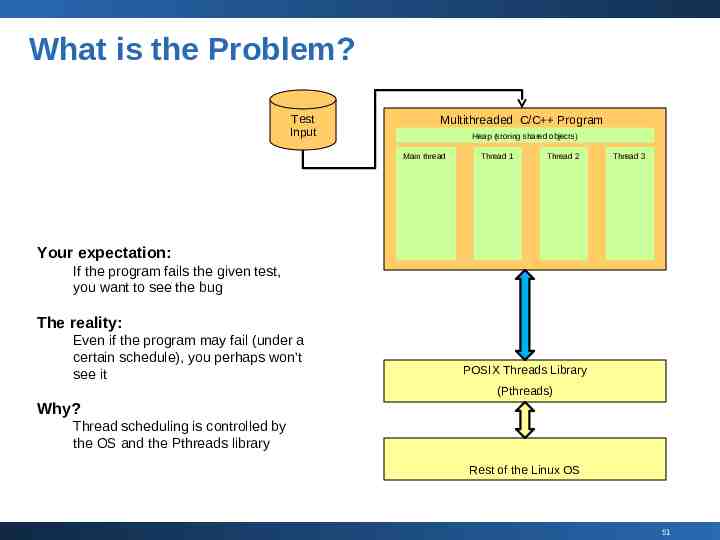
What is the Problem? Test Input Multithreaded C/C Program Heap (storing shared objects) Main thread Thread 1 Thread 2 Thread 3 Your expectation: If the program fails the given test, you want to see the bug The reality: Even if the program may fail (under a certain schedule), you perhaps won’t see it POSIX Threads Library (Pthreads) Why? Thread scheduling is controlled by the OS and the Pthreads library Rest of the Linux OS 51

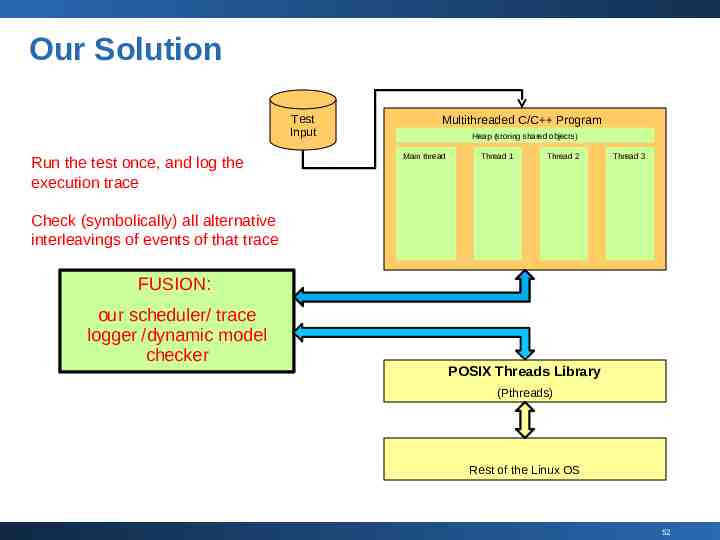
Our Solution Test Input Run the test once, and log the execution trace Multithreaded C/C Program Heap (storing shared objects) Main thread Thread 1 Thread 2 Thread 3 Check (symbolically) all alternative interleavings of events of that trace FUSION: our scheduler/ trace logger /dynamic model checker POSIX Threads Library (Pthreads) Rest of the Linux OS 52

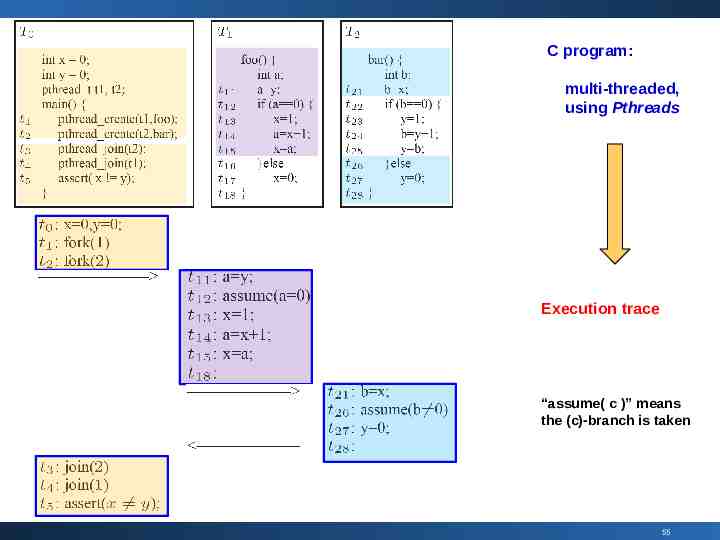
Predictive Analysis Detecting errors by statically analyzing the recorded execution traces of a concurrent program without re-running the program 53

Given a concrete trace (logged during execution) some properties (e.g. embedded assertions) Checking whether the properties hold in all possible interleavings of events of that trace Symbolically, using a SMT solver 54

C program: multi-threaded, using Pthreads Execution trace “assume( c )” means the (c)-branch is taken 55

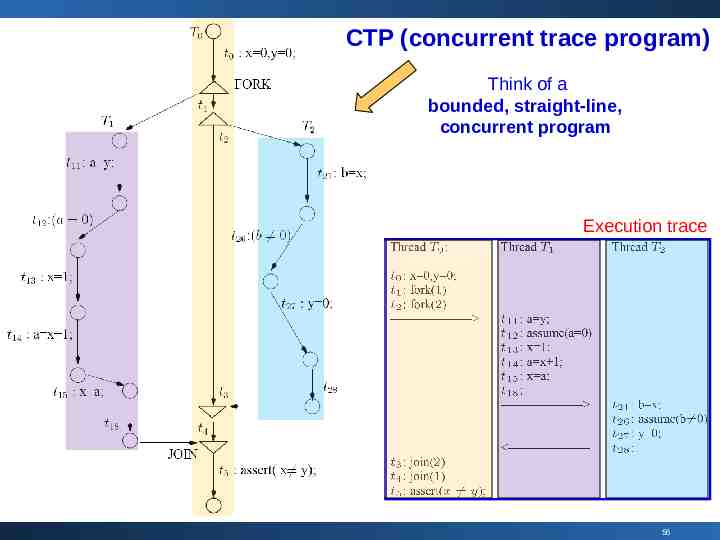
CTP (concurrent trace program) Think of a bounded, straight-line, concurrent program Execution trace 56

Detecting Violations (symbolically) Build a SAT formula (in some quantifier-free first-order logic) F program : any feasible thread interleaving of CTP F property : assertion is violated Solve ( F program & F property ) Sat found a real error Unsat 57

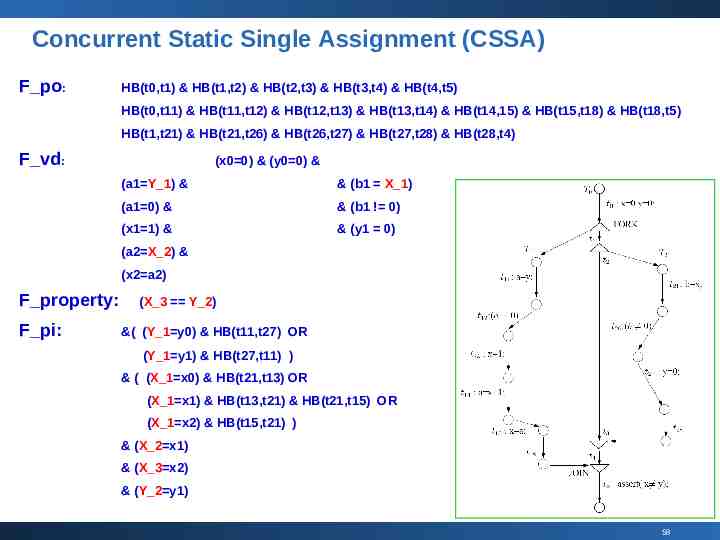
Concurrent Static Single Assignment (CSSA) F po: HB(t0,t1) & HB(t1,t2) & HB(t2,t3) & HB(t3,t4) & HB(t4,t5) HB(t0,t11) & HB(t11,t12) & HB(t12,t13) & HB(t13,t14) & HB(t14,15) & HB(t15,t18) & HB(t18,t5) HB(t1,t21) & HB(t21,t26) & HB(t26,t27) & HB(t27,t28) & HB(t28,t4) F vd: (x0 0) & (y0 0) & (a1 Y 1) & & (b1 X 1) (a1 0) & & (b1 ! 0) (x1 1) & & (y1 0) (a2 X 2) & (x2 a2) F property: F pi: (X 3 Y 2) &( (Y 1 y0) & HB(t11,t27) OR (Y 1 y1) & HB(t27,t11) ) & ( (X 1 x0) & HB(t21,t13) OR (X 1 x1) & HB(t13,t21) & HB(t21,t15) OR (X 1 x2) & HB(t15,t21) ) & (X 2 x1) & (X 3 x2) & (Y 2 y1) 58

HB (Happens-Before) Constraints How is HB(t1,t2) implemented? Event t1 happens strictly before t2 HB(t1,t2) : t1 t2 where t1,t2 are integer variables 59

Outline Motivation Symbolic Predictive Analysis Related Work Context Bounding (SAT-based) Experiments Conclusions 60

Related Work (predicting errors) Methods that do not miss errors (over-approximate) Lockset methods: e.g. Eraser, RacerX Problem: False alarms (sometimes, lots of them) Methods with no bogus errors (under-approximate) Inspired by Lamport’s happens-before causality Recent causal models Generalized Predictive Analysis [Sen,Rosu,Agha,2005] Parametric and Sliced Causality [Chen,Rosu,2007] Maximal Causal Model [Serbanuta,Chen,Rosu,2008] – Subsume other causal models 61

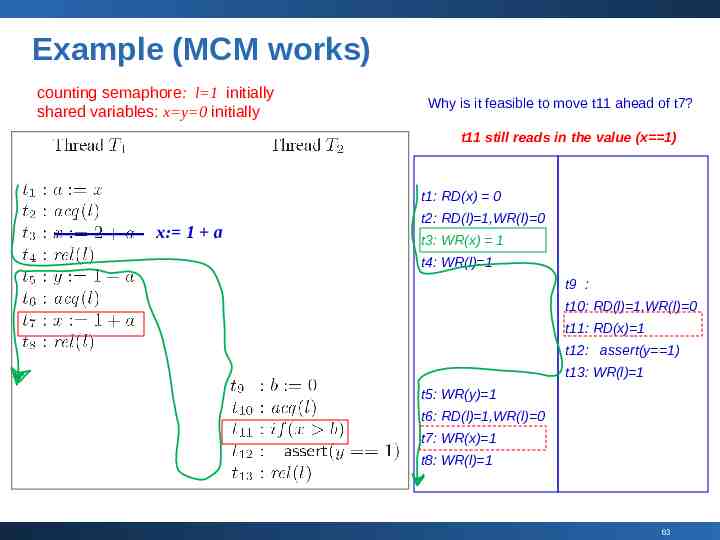
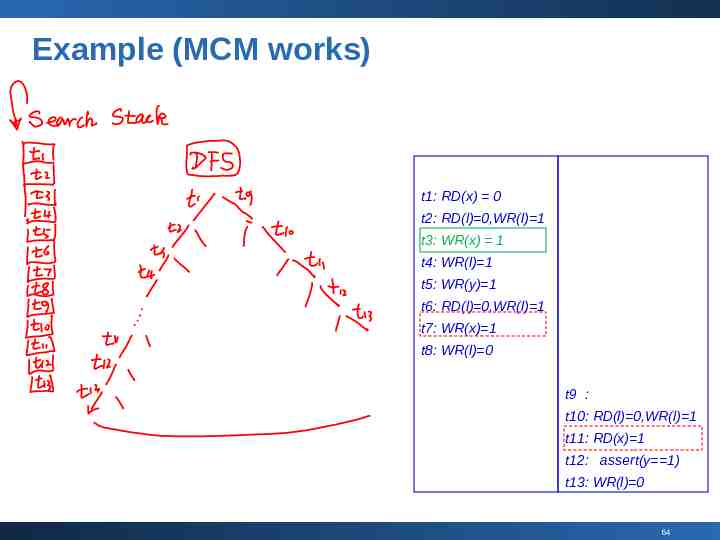
Example (MCM works) counting semaphore: l 1 initially shared variables: x y 0 initially The View of Maximal Causal Model observe “events” instead of “statements” t1: RD(x) 0 x: 1 a t2: RD(l) 1,WR(l) 0 t3: WR(x) 1 t4: WR(l) 1 t5: WR(y) 1 t6: RD(l) 1,WR(l) 0 t7: WR(x) 1 t8: WR(l) 1 t9 : t10: RD(l) 1,WR(l) 0 t11: RD(x) 1 t12: assert(y 1) t13: WR(l) 1 62

Example (MCM works) counting semaphore: l 1 initially shared variables: x y 0 initially Why is it feasible to move t11 ahead of t7? t11 still reads in the value (x 1) t1: RD(x) 0 x: 1 a t2: RD(l) 1,WR(l) 0 t3: WR(x) 1 t4: WR(l) 1 t9 : t10: RD(l) 1,WR(l) 0 t11: RD(x) 1 t12: assert(y 1) t13: WR(l) 1 t5: WR(y) 1 t6: RD(l) 1,WR(l) 0 t7: WR(x) 1 t8: WR(l) 1 63

Example (MCM works) t1: RD(x) 0 t2: RD(l) 0,WR(l) 1 t3: WR(x) 1 t4: WR(l) 1 t5: WR(y) 1 t6: RD(l) 0,WR(l) 1 t7: WR(x) 1 t8: WR(l) 0 t9 : t10: RD(l) 0,WR(l) 1 t11: RD(x) 1 t12: assert(y 1) t13: WR(l) 0 64

Example (MCM will miss real errors) counting semaphore: l 1 initially shared variables: x y 0 initially MCM will miss this real error t1: RD(x) 0 x: 1 a t2: RD(l) 0,WR(l) 1 t3: WR(x) 2 t4: WR(l) 1 t5: WR(y) 1 t6: RD(l) 0,WR(l) 1 t7: WR(x) 1 t8: WR(l) 0 t9 : t10: RD(l) 0,WR(l) 1 t11: RD(x) 1 t12: assert(y 1) t13: WR(l) 0 65

Using CTP (will catch the real error) 66

Outline Motivation Symbolic Predictive Analysis Related Work Context Bounding (SAT-based) Experiments Conclusions 67

Outline Motivation Symbolic Analysis Related Work Context Bounding (SAT-based) Experiments Conclusions 72

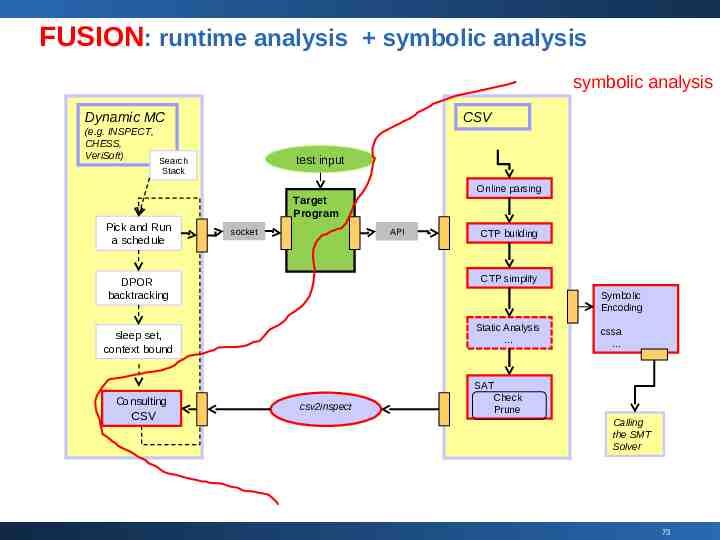
FUSION: runtime analysis symbolic analysis symbolic analysis Dynamic MC CSV (e.g. INSPECT, CHESS, VeriSoft) Search test input Stack Online parsing Target Program Pick and Run a schedule socket API CTP building CTP simplify DPOR backtracking Symbolic Encoding Static Analysis sleep set, context bound cssa SAT Consulting CSV csv2inspect Check Prune Calling the SMT Solver 73

Experiments Benchmarks Multithreaded C programs (Linux/Pthreads) With embedded assertions Details Indexer examples Multiple threads sharing a hash table 11 threads or less, no hash collision 12 threads or more, heavy hash collision Bank examples PDPS 2003] from [Flanagan & Godefroid, POPL 2005] from [Farchi, Nir, Ur, Small programs with pointers, arrays, and structures, 74

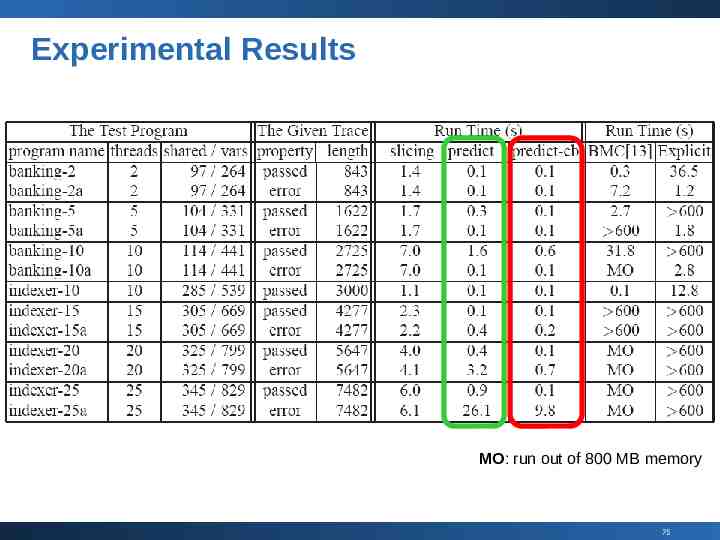
Experimental Results MO: run out of 800 MB memory 75

Conclusions New method: symbolic predictive analysis Coverage: subsumes known causal models (MCM) Efficiency: SAT-based search vs. explicit enumeration Highlights CTP (Concurrent Trace Program) CSSA (Concurrent Static Single Assignment) SAT-based context bounding Future work Predicting atomicity violations 76

References SMT “Satisfiability Modulo Theories” (book chapter) Clark Barrett, Roberto Sebastiani, Sanjit A. Seshia, and Cesare Tinelli. In the Handbook of Satisfiability, IOS Press, 2009. (available from the authors’ web pages) Concurrent Software Verification “Symbolic Predictive Analysis for Concurrent Programs”, FM 2009 Chao Wang, Sudipta Kundu, Malay Ganai, and Aarti Gupta “Trace based Symbolic Analysis for Atomicity Violations”, TACAS 2010 Chao Wang, Rhishikesh Limaye, Malay Ganai, and Aarti Gupta (available from the authors’ web pages) 77