Section 2.9 Maximum Flow Problems Minimum Cost Network Flows Shortest

Section 2.9 Maximum Flow Problems Minimum Cost Network Flows Shortest Path Problems

Maximum Flow Problems Reference: Network Flows by Ahuja, Magnanti, and Orlin

Background In a capacitated network, we wish to send as much flow as possible between two special nodes, a source node s and a sink node t, without exceeding the capacity of any arc. The problem reportedly rose in relation to the rail networks of the Soviet Union, during the 1950's. The US wanted to know how quickly the Soviet Union could get supplies through its rail network to its satellite states in Eastern Europe. In addition, the US wanted to know which rails it could destroy most easily to cut off the satellite states from the rest of the Soviet Union. It turned out that these two problems were closely related, and that solving the max flow problem also solves the min cut problem of figuring out the cheapest way to cut off the Soviet Union from its satellites. Additional reference: The Importance of Algorithms by Ibackstrom from www.topcoder.com

Assumptions The network is directed. All capacities are nonnegative integers. The network does not contain a directed path from node s to node t composed only of infinite capacity arcs. Whenever an arc (i,j) belongs to A, arc (j,i) also belongs to A. The network does not contain parallel arcs.

Max Flow General Formulation The standard LP formulation of the Maximum s-t Flow problem adds a dummy Return arc, (t,s), to the network in question, and then maximizes the flow on this arc. The capacity of the return arc is unbounded, and the rest of the formulation consists of balance of flow and capacity constraints. max X t , s s.t. j:( i , j ) A X ij X ji 0 i V j:( j ,i ) A 0 X ij uij for each (i, j ) A

Network Flow Model Let V denote the set of nodes and A denote the set of arcs in our network G. At each node i V , let si denote the supply at node i, and d j the demand at node j , and define bi si d i ; we shall assume that b 0, i i V that is, the total amount of supply in the network equals the total demand. The Minimum Cost Network Flow Problem is given by min cij X ij X ij ( i , j ) A s.t. j:( i , j ) A X ki bi , i V k :( k ,i ) A X ij 0, (i , j ) A

Importance of Network Models Claim 2.1 – Nearly all network models can be formulated as minimum cost network flow problems Claim 2.2 – Any problem modeled as a minimum cost network flow problem has an optimal solution that has only integer values, provided each supply and each demand has integral value

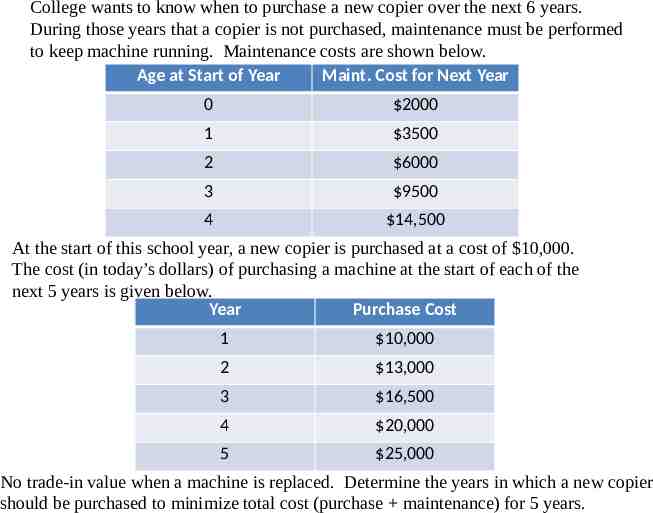
College wants to know when to purchase a new copier over the next 6 years. During those years that a copier is not purchased, maintenance must be performed to keep machine running. Maintenance costs are shown below. Age at Start of Year Maint. Cost for Next Year 0 2000 1 3500 2 6000 3 9500 4 14,500 At the start of this school year, a new copier is purchased at a cost of 10,000. The cost (in today’s dollars) of purchasing a machine at the start of each of the next 5 years is given below. Year Purchase Cost 1 10,000 2 13,000 3 16,500 4 20,000 5 25,000 No trade-in value when a machine is replaced. Determine the years in which a new copier should be purchased to minimize total cost (purchase maintenance) for 5 years.

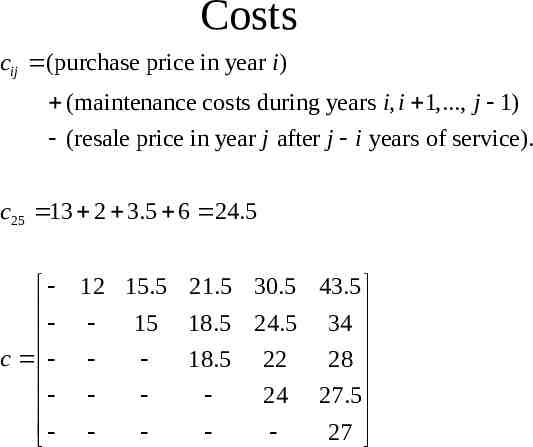
Costs cij (purchase price in year i) (maintenance costs during years i, i 1,., j 1) (resale price in year j after j i years of service). c25 13 2 3.5 6 24.5 c 12 15.5 21.5 30.5 43.5 15 18.5 24.5 34 18.5 22 28 24 27.5 27

Formulation min cij X ij ( i , j ) A s.t. X 12 X 13 X 14 X 15 X 16 1 X 23 X 24 X 25 X 26 X 12 0 X 34 X 35 X 36 X 13 X 23 0 X 45 X 46 X 14 X 24 X 34 0 X 56 X 15 X 25 X 35 X 45 0 X 16 X 26 X 36 X 46 X 56 1 X ij 0, (i, j ) A