RSA A public Key Algorithm

RSA A public Key Algorithm

RSA by Rivest, Shamir & Adleman of MIT in 1977 based on exponentiation in a finite (Galois) field over integers modulo a prime. It supports key management concept, it is key generation.

RSA RSA makes the public and prívate keys by multiplying two large prime numbers p and q Its easy to find & multiply large prime No. (n pq) It is very difficult to factor the number n to find p and q Finding the private key from the public key would require a factoring operation The real challenge is the selection & generation of keys. RSA is complex and slow, but secure 100 times slower than DES on s/w & 1000 times on h/w.

Algorithm 1. P, Q 2. N P*Q 3. E such that it is not a factor of (P-1)*(Q-1) 4. (D*E) mod (P-1)*(Q-1) 1 5. CT PTE mod N 6. Send CT 7. PT CTD mod N

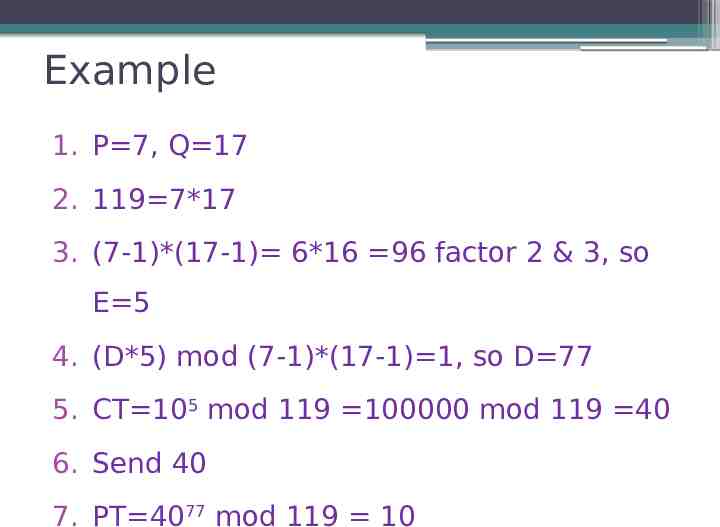
Example 1. P 7, Q 17 2. 119 7*17 3. (7-1)*(17-1) 6*16 96 factor 2 & 3, so E 5 4. (D*5) mod (7-1)*(17-1) 1, so D 77 5. CT 105 mod 119 100000 mod 119 40 6. Send 40 7. PT 4077 mod 119 10

RSA Security It uses prime number theory which make it difficult to find out the key by reverse engineering. Mathematical Research suggests that it would take more than 70 years to find P & Q if N is a 100 digit number.

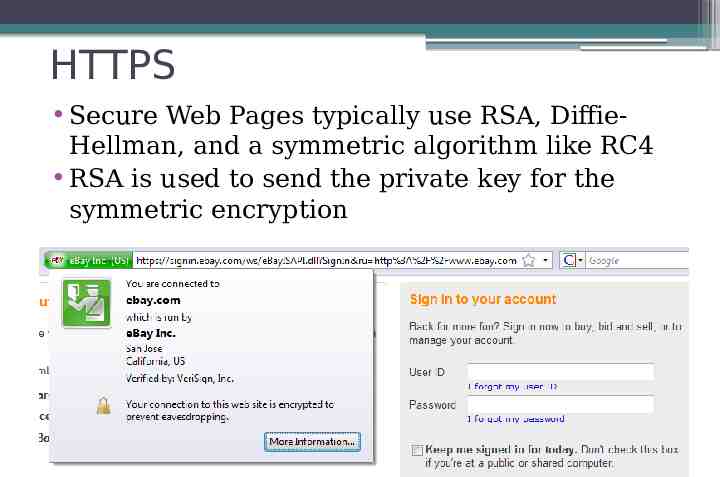
HTTPS Secure Web Pages typically use RSA, DiffieHellman, and a symmetric algorithm like RC4 RSA is used to send the private key for the symmetric encryption

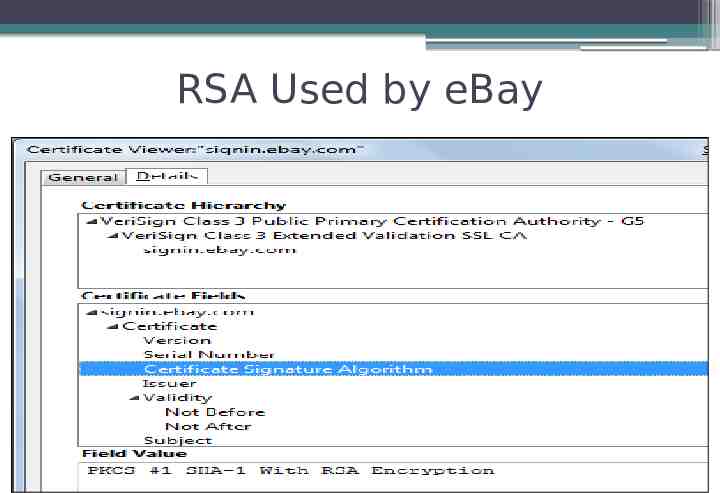
RSA Used by eBay