Reinforced Concrete Design-4 Design of doubly reinforced beams By Dr.

Reinforced Concrete Design-4 Design of doubly reinforced beams By Dr. Attaullah Shah Swedish College of Engineering and Technology Wah Cantt.

Due to size limitations compression reinforcement may be required in addition to anchor bars to support stirrups. If the applied ultimate moment is more than the factored nominal capacity allowed by maximum steel ratio, the additional steel may be required in compression and tension to support the excess moment.

Analysis of Doubly Reinforced Sections Effect of Compression Reinforcement on the Strength and Behavior Less concrete is needed to resist the T and thereby moving the neutral axis (NA) up. T As f y C T

Analysis of Doubly Reinforced Sections Effect of Compression Reinforcement on the Strength and Behavior Singly Reinforced a1 C Cc ; M n As f y d 2 Doubly Reinforced a2 C Cc C s ; M n As f y d 2 and a2 a1

Reasons for Providing Compression Reinforcement Reduced sustained load deflections. Creep of concrete in compression zone transfer load to compression steel reduced stress in concrete less creep less sustained load deflection

Doubly Reinforced Beams Four Possible Modes of Failure Under reinforced Failure ( Case 1 ) Compression and tension steel yields ( Case 2 ) Only tension steel yields Over reinforced Failure ( Case 3 ) Only compression steel yields ( Case 4 ) No yielding Concrete crushes

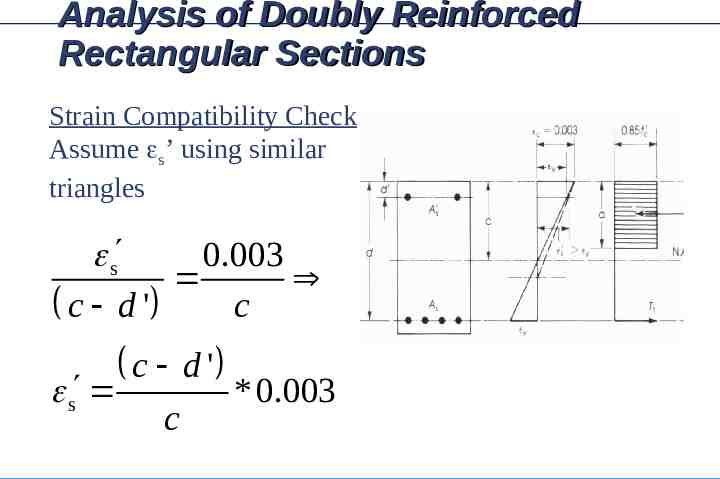
Analysis of Doubly Reinforced Rectangular Sections Strain Compatibility Check Assume s’ using similar triangles s 0.003 c c d ' c s c d ' * 0.003

Analysis of Doubly Reinforced Rectangular Sections Strain Compatibility Using equilibrium and find a As As f y T Cc Cs a 0.85 f c b As As f y ' d f y a c 1 1 0.85 f c b 1 0.85 f c

Analysis of Doubly Reinforced Rectangular Sections Strain Compatibility The strain in the compression steel is d s 1 cu c 1 0.85 f c d 1 0.003 ' d f y

Analysis of Doubly Reinforced Rectangular Sections Strain Compatibility Confirm s y fy Es ; s y fy fy 1 0.85 f c d s 1 0.003 3 E s 29 x 10 ksi ' d f y

Analysis of Doubly Reinforced Rectangular Sections Strain Compatibility Confirm 1 0.85 f c d f y 87 87 ' d f y 1 0.85 f c d 87 ' d f 87 f y y

Analysis of Doubly Reinforced Rectangular Sections Find c As f y 0.85 f c ba As f y Ass As f y c 0.85 f c b 1 a 1c confirm that the tension steel has yielded fy d c s cu y Es c

Analysis of Doubly Reinforced Rectangular Sections If the statement is true than a M n As As f y d As f y d d 2 else the strain in the compression steel f s E s

Analysis of Doubly Reinforced Rectangular Sections Return to the original equilibrium equation As f y As fs 0.85 f cba As Es s 0.85 f cb 1c d As Es 1 cu 0.85 f c b 1c c

Analysis of Doubly Reinforced Rectangular Sections Rearrange the equation and find a quadratic equation d As f y As Es 1 cu 0.85 f cb 1c c 2 0.85 f cb 1c As Es cu As f y c As Es cu d 0 Solve the quadratic and find c.

Analysis of Doubly Reinforced Rectangular Sections Find the fs’ d d f s 1 Es cu 1 87 ksi c c Check the tension steel. fy d c s cu y Es c

Analysis of Doubly Reinforced Rectangular Sections Another option is to compute the stress in the compression steel using an iterative method. 0.85 f d 1 c 3 f s 29 x 10 1 0.003 ' d f y

Analysis of Doubly Reinforced Rectangular Sections Go back and calculate the equilibrium with fs’ Af T C C a s y c a c 1 s As f s 0.85 f c b Iterate until the c value is adjusted for the fs’ until the stress converges. d fs 1 87 ksi c

Analysis of Doubly Reinforced Rectangular Sections Compute the moment capacity of the beam a M n As f y As fs d As fs d d 2

Limitations on Reinforcement Ratio for Doubly Reinforced beams Lower limit on min 3 f c 200 fy fy same as for single reinforce beams. (ACI 10.5)

Example: Doubly Reinforced Section Given: f’c 4000 psi fy 60 ksi A’s 2 #5 As 4 #7 d’ 2.5 in. d 15.5 in h 18 in. b 12 in. Calculate Mn for the section for the given compression steel.

Example: Doubly Reinforced Section Compute the reinforcement coefficients, the area of the bars #7 (0.6 in2) and #5 (0.31 in2) As 4 0.6 in 2 2.4 in 2 As 2 0.31 in 2 0.62 in 2 As 2.4 in 2 0.0129 bd 12 in. 15.5 in. As 0.62 in 2 0.0033 bd 12 in. 15.5 in.

Example: Doubly Reinforced Section Compute the effective reinforcement ratio and minimum 0.0129 0.0033 0.00957 eff 200 200 0.00333 fy 60000 3 f c 3 4000 or 0.00316 fy 60000 min 0.0129 0.00333 OK!

Example: Doubly Reinforced Section Compute the effective reinforcement ratio and minimum 1 0.85 f c d 87 ' d fy 87 f y 0.85 0.85 4 ksi 2.5 in. 87 0.0398 87 60 60 ksi 15.5 in. 0.00957 0.0398 Compression steel has not yielded.

Example: Doubly Reinforced Section Instead of iterating the equation use the quadratic method 0.85 f cb 1c 2 As Es cu As f y c As Es cu d 0 0.85 4 ksi 12 in. 0.85 c 2 0.62 in 2 29000 ksi 0.003 2.4 in 2 60 ksi c 0.62 in 2 29000 ksi 0.003 2.5 in. 0 34.68c 2 90.06c 134.85 0 c 2 2.5969c 3.8884 0

Example: Doubly Reinforced Section Solve using the quadratic formula 2 c 2.5969c 3.8884 0 c 2.5969 c 3.6595 in. 2.5969 2 2 4 3.8884

Example: Doubly Reinforced Section Find the fs’ d 2.5 in. f s 1 Es cu 1 87 ksi c 3.659 in. 27.565 ksi Check the tension steel. 15.5 in. 3.659 in. s 0.003 0.00971 0.00207 3.659 in.

Example: Doubly Reinforced Section Check to see if c works c As f y As fs 0.85 f c 1b 2 2 2.4 in 60 ksi 0.62 in 27.565 ksi c 3.659 in. The problem worked 0.85 4 ksi 0.85 12 in.

Example: Doubly Reinforced Section Compute the moment capacity of the beam a M n As f y As f s d As fs d d 2 2.4 in 2 60 ksi 0.85 3.659 in. 15.5 in. 2 2 0.62 in 27.565 ksi 0.62 in 2 27.565 ksi 15.5 in. 2.5 in. 1991.9 k - in. 166 k - ft

Example: Doubly Reinforced Section If you want to find the Mu for the problem c 3.66 in. 0.236 d 15.5 in. From ACI (figure R9.3.2)or figure (pg 100 in your c text) 0.375 d 0.9 The resulting ultimate moment is M u M u 0.9 166 k - ft 149.4 k - ft