Public-Key (Asymmetric) Ciphers Part 1 Slides Original Source: 1.

Public-Key (Asymmetric) Ciphers Part 1 Slides Original Source: 1. M. Stamp, “Information Security: Principles and Practice,” John Wiley 2. C. Paar and J. Pelzl, “Understanding Cryptography – A Textbook for Students and Practitioners,” Springer ( www.crypto-textbook.com) 3. B. Forouzan, ” Cryptography and Network Security,” McGraw-Hill

Outline Motivation Principles behind public-key ciphers Prime numbers & Modulo operation 2/31

Outline Motivation Principles behind public-key ciphers Prime numbers & Modulo operation 3/31

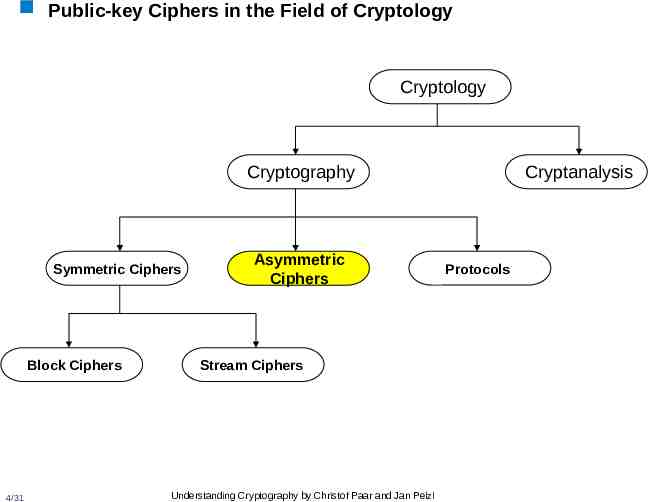
Public-key Ciphers in the Field of Cryptology Cryptology Cryptography Symmetric Ciphers Block Ciphers 4/31 Asymmetric Ciphers Stream Ciphers Understanding Cryptography by Christof Paar and Jan Pelzl Cryptanalysis Protocols

Issues with Symmetric-key Ciphers Symmetric-key ciphers (e.g., AES or 3DES) are very secure, fast, and widespread but: Key distribution problem: Secret key must be transported securely Number of keys: In a network, each pair of users requires a unique key n users in the network require keys with each user storing (n – 1) keys!! Cheating: Alice or Bob can cheat each other, because they have identical keys!!! Repudiation by Alice Fabrication by Bob 5/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Outline Motivation Principles behind public-key ciphers Prime numbers & Modulo operation 6/31

Public-Key Cryptography Two keys o Sender uses recipient’s public key to encrypt o Recipient uses private key to decrypt Based on “trap door one way function” o “One way” means easy to compute in one direction, but hard to compute in other direction o “Trap door” used to create key pairs 7

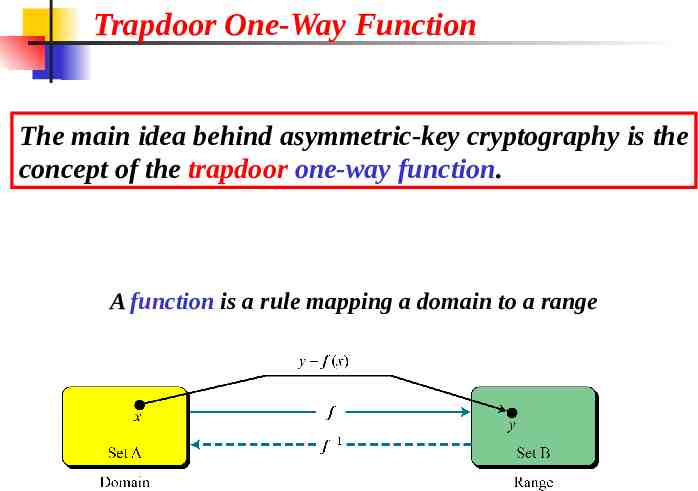
Trapdoor One-Way Function The main idea behind asymmetric-key cryptography is the concept of the trapdoor one-way function. A function is a rule mapping a domain to a range

Trapdoor One-Way Function (Continued) One-Way Function (OWF) 1. f is easy to compute. 2. f 1 is difficult to compute. Trapdoor One-Way Function (TOWF) 3. Given y and a trapdoor k’, x can be computed easily. 10.9

10.1.4 Continued Example 10. 1 When n is large, n p q is a one-way function. Given p and q, it is always easy to calculate n; given n, it is very difficult to compute p and q. This is the factorization problem. Example 10. 2 When n is large, the function y xk mod n is a trapdoor one-way function. Given x, k, and n, it is easy to calculate y. Given y, k, and n, it is very difficult to calculate x. This is the discrete logarithm problem. However, if we know the trapdoor, k′, such that k k′ 1 mod f(n), we can use x yk′ mod n to easily find x.

How to build Public-Key Algorithms One way functions are based on mathematically hard problems Three main families: Factoring integers (RSA, .) Given a composite integer n, find its prime factors Multiply two primes: easy Discrete Logarithm (DL) (Diffie-Hellman, Elgamal, DSA, ) Given a, y and m, find x such that y ax mod m Exponentiation ax : easy Elliptic Curves (EC) (ECDH, ECDSA) Generalization of discrete logarithm Note: The problems are considered mathematically hard, but no proof exists (so far) 11/31 Understanding Cryptography by Christof Paar and Jan Pelzl

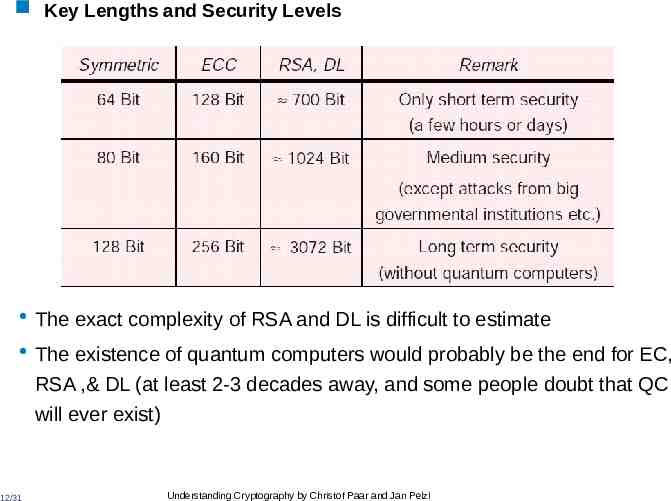
Key Lengths and Security Levels The exact complexity of RSA and DL is difficult to estimate The existence of quantum computers would probably be the end for EC, RSA ,& DL (at least 2-3 decades away, and some people doubt that QC will ever exist) 12/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Public-Key Cryptography Encryption o Suppose we encrypt M with Bob’s public key o Bob’s private key can decrypt to recover M Digital Signature o Sign by “encrypting” with your private key o Anyone can verify signature by “decrypting” with public key o But only you could have signed o Like a handwritten signature, but way better 13

Outline Motivation Principles behind public-key ciphers Prime numbers & Modulo operation 14/31

Modular Addition/Multiplication Notation and facts o o o o 7 mod 6 1 7 13 1 mod 6 ((a mod n) (b mod n)) mod n (a b) mod n ((a mod n)(b mod n)) mod n ab mod n Addition Examples o o o o o 3 5 2 mod 6 2 4 0 mod 6 3 3 0 mod 6 (7 12) mod 6 19 mod 6 1 mod 6 (7 12) mod 6 (1 0) mod 6 1 mod 6 15

Modular Addition/Multiplication Multiplication Examples o o o o o 3 4 0 (mod 6) 2 4 2 (mod 6) 5 5 1 (mod 6) (7 4) mod 6 28 mod 6 4 mod 6 (7 4) mod 6 (1 4) mod 6 4 mod 6 16

Modular Inverses Additive inverse of x mod n, denoted –x mod n, is the number that must be added to x to get 0 mod n o -2 mod 6 4, since 2 4 0 mod 6 Multiplicative inverse of x mod n, denoted x-1 mod n, is the number that must be multiplied by x to get 1 mod n o 3-1 mod 7 5, since 3 5 1 mod 7 17

Modular Arithmetic Quiz Q: What is -3 mod 6? A: 3 Q: What is -1 mod 6? A: 5 Q: What is 5-1 mod 6? A: 5 Q: What is 2-1 mod 6? A: No number works! Multiplicative inverse might not exist 18

Relative Primality x and y are relatively prime if they have no common factor other than 1 x-1 mod y exists only when x and y are relatively prime If it exists, x-1 mod y is easy to compute using Extended Euclidean Algorithm (more later!) 19

Euler’s Totient Function (n) is “the number of numbers less than n that are relatively prime to n” o Here, “numbers” are positive integers Examples o o o o o (4) 2 since 4 is relatively prime to 3 and 1 (5) 4 since 5 is relatively prime to 1,2,3,4 (12) 4 (p) p - 1 if p is prime (pq) (p - 1)(q - 1) if p and q prime 20

Euclidean Algorithm Compute the greatest common divisor gcd (r0, r1) of two integers r0 and r1 gcd is easy for small numbers: 1. factor r0 and r1 2. gcd highest common factors Example: r0 84 2 . 2 . 3 . 7 r1 30 2 . 3 . 5 The gcd is the product of all common prime factors 2 . 3 6 gcd (30,84) Factoring is complicated for large numbers 21/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Euclidean Algorithm Observation: gcd (r0, r1) gcd (r0 – r1, r1) Reduce the problem of finding gcd of two numbers to that of the gcd of two smaller numbers Repeat process recursively The final gcd (ri, 0) ri is the answer! gcd can be computed as follows: gcd (a, 0) a gcd (a, b) gcd (b, a mod b) –– faster than gcd (a – b, b) but same result! Example: gcd (30, 18) gcd (18, 30 mod 18) gcd (18, 12) gcd (12, 18 mod 12) gcd (12, 6) gcd (6, 12 mod 6) gcd (6, 0) 6 Note: complexity of method grows linearly with the number of bits (great!) 22/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Extended Euclidean Algorithm (EEA) Very important for public-key ciphers Extend the Euclidean algorithm to r1-1 mod r0 EEA computes s,t, and the gcd: Use the relation for mod r0 Compare with the definition of modular inverse: t r1-1 mod r0 Note: r0 and r1 must be relatively prime for the inverse to exist (i.e., gcd (r0, r1) 1) Recursive formulae to calculate s & t in each step (next slide) EEA can be used to find multiplicative inverses in Galois fields 23/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Extended Euclidean Algorithm 24/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Extended Euclidean Algorithm stop when ri 1 25/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Euler’s Phi (Totient) Function 1/3 26/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Euler’s Phi (Totient) Function 2/3 27/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Euler’s Phi (Totient) Function 3/3 (n) can be computed recursively by: 1. (1) 1 2. if n is a prime power, n pe, then (n) (p – 1) p(e – 1) 3. if gcd(m, n) 1, then (mn) (m) . (n) Examples: (17) 16 (25) 52 (5 – 1) . 5 20 (16) 24 (2 – 1) . 23 8 (105) (3 . (5 . 7)) 2 . (4 . 6) 48 (200) (23 . 52) ((2 – 1) . 22) ((5 – 1) . 5) 4 . 20 80 28/31

Fermat’s Little Theorem Very useful in public-key ciphers (e.g., primality testing while generating keys) Recall that arithmetic in finite fields GF(p) is done modulo p theorem holds for all integers a GF(p) Alternate form: ap a 1 ap 1 1 (mod p) (why?) a ap 2 1 (mod p) a 1 ap 2 (mod p) Quick way to find mult. inverse if modulus is a prime!! But slower than EEA unless a hardware accelerator is used for fast exponentiation Example: Let p 7 and a 2 a 1 ap 2 25 32 4 mod 7 29/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Euler’s Theorem Generalization of Fermat’s Little Theorem for any modulus Example: Let m 12 and a 5 gcd (12, 5) 1 (12) (22 · 3) (22 21)(31 30) 4 Verify: 5 (12) 54 625 1 mod 12 Theorem is used to prove correctness of RSA (most popular public-key crypto) 30/31 Understanding Cryptography by Christof Paar and Jan Pelzl

Euler’s Theorem Another important use of Euler’s theorem is the following: if k j (mod (n)) then ak aj mod n Helps in exponentiation computation (needed in RSA) Example 1: 246 22 (mod 5), since 46 2 (mod (5)) Example 2: Compute the following: a. 1452 (mod 11) 1452 352 (mod 11). Since (11) 10 52 2 (mod 10) 1452 352 32 9 (mod 11) b. 46391 (mod 15) 46391 1391 (–2)91 (mod 15). Since (15) 2 4 8 91 3 (mod 8) (–2)91 (–2)3 –8 7 (mod 15) 31/31 Understanding Cryptography by Christof Paar and Jan Pelzl