Prolog Programming slides written by Dr W.F. Clocksin

Prolog Programming slides written by Dr W.F. Clocksin

The Plan An example program Syntax of terms Some simple programs Terms as data structures, unification The Cut Writing real programs

What is Prolog? Prolog is the most widely used language to have been inspired by logic programming research. Some features: Prolog uses logical variables. These are not the same as variables in other languages. Programmers can use them as ‘holes’ in data structures that are gradually filled in as computation proceeds.

More Unification is a built-in termmanipulation method that passes parameters, returns results, selects and constructs data structures. Basic control flow model is backtracking. Program clauses and data have the same form. The relational form of procedures makes it possible to define ‘reversible’ procedures.

More Clauses provide a convenient way to express case analysis and nondeterminism. Sometimes it is necessary to use control features that are not part of ‘logic’. A Prolog program can also be seen as a relational database containing rules as well as facts.

What a program looks like /* At the Zoo */ elephant(george). elephant(mary). panda(chi chi). panda(ming ming). dangerous(X) :- big teeth(X). dangerous(X) :- venomous(X). guess(X, tiger) :- stripey(X), big teeth(X), isaCat(X). guess(X, koala) :- arboreal(X), sleepy(X). guess(X, zebra) :- stripey(X), isaHorse(X).

Prolog is a ‘declarative’ language Clauses are statements about what is true about a problem, instead of instructions how to accomplish the solution. The Prolog system uses the clauses to work out how to accomplish the solution by searching through the space of possible solutions. Not all problems have pure declarative specifications. Sometimes extralogical statements are needed.

Example: Concatenate lists a and b list procedure cat(list a, list b) { In an imperative language list t list u copylist(a); while (t.tail ! nil) t t.tail; t.tail b; return u; } In a functional language cat(a,b) if b nil then a else cons(head(a), cat(tail(a),b)) cat([], Z, Z). In a declarative language cat([H T], L, [H Z]) :- cat(T, L, Z).

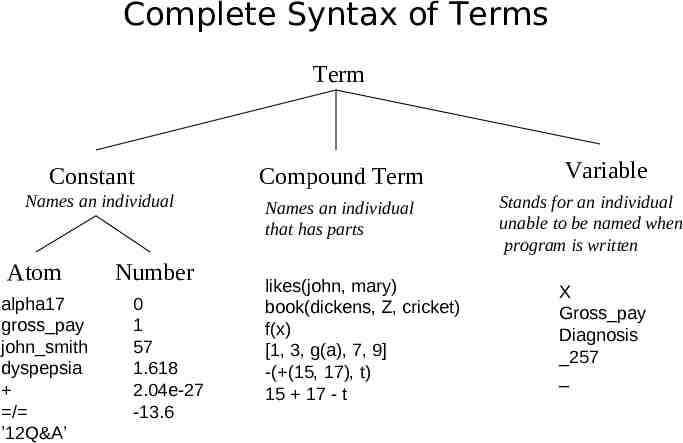
Complete Syntax of Terms Term Constant Names an individual Atom alpha17 gross pay john smith dyspepsia / ’12Q&A’ Number 0 1 57 1.618 2.04e-27 -13.6 Compound Term Names an individual that has parts likes(john, mary) book(dickens, Z, cricket) f(x) [1, 3, g(a), 7, 9] -( (15, 17), t) 15 17 - t Variable Stands for an individual unable to be named when program is written X Gross pay Diagnosis 257

Compound Terms The parents of Spot are Fido and Rover. parents(spot, fido, rover) Functor (an atom) of arity 3. components (any terms) It is possible to depict the term as a tree: parents spot fido rover

Compound Terms Some atoms have built-in operator declarations so they may be written in a syntactically convenient form. The meaning is not affected. This example looks like an arithmetic expression, but might not be. It is just a term. / / (15 X, (0*a) (2 5)) 15 * X 0 a 2 5

More about operators Any atom may be designated an operator. The only purpose is for convenience; the only effect is how the term containing the atom is parsed. Operators are ‘syntactic sugar’. We won’t be designating operators in this course, but it is as well to understand them, because a number of atoms have built-in designations as operators. Operators have three properties: position, precedence and associativity. more

Examples of operator properties Position Prefix: Infix: Postfix: Operator Syntax Normal Syntax -2 -(2) 5 17 (17,5) N! !(N) Associativity: left, right, none. X Y Z is parsed as (X Y) Z because addition is left-associative. These are all the same as the normal rules of arithmetic. Precedence: an integer. X Y*Z is parsed as X (Y*Z) because multiplication has higher precedence.

The last point about Compound Terms Constants are simply compound terms of arity 0. badger means the same as badger()

Structure of Programs Programs consist of procedures. Procedures consist of clauses. Each clause is a fact or a rule. Programs are executed by posing queries. An example

Example Predicate Procedure for elephant Facts Clauses Rule elephant(george). elephant(mary). elephant(X) :- grey(X), mammal(X), hasTrunk(X).

Example Queries ?- elephant(george). yes ?- elephant(jane). Replies no

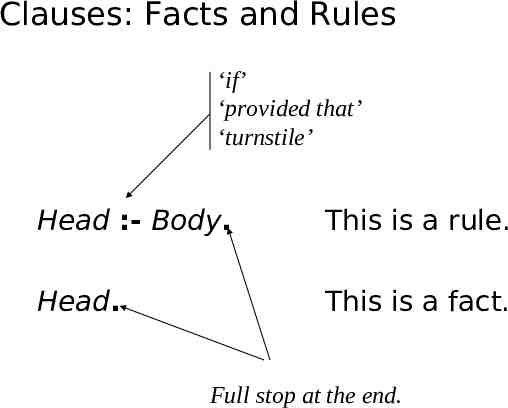
Clauses: Facts and Rules ‘if’ ‘provided that’ ‘turnstile’ Head :- Body. This is a rule. Head. This is a fact. Full stop at the end.

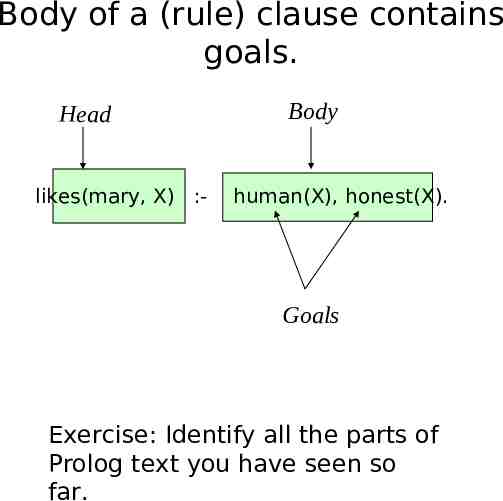
Body of a (rule) clause contains goals. Head likes(mary, X) :- Body human(X), honest(X). Goals Exercise: Identify all the parts of Prolog text you have seen so far.

Interpretation of Clauses Clauses can be given a declarative reading or a procedural reading. Form of clause: Declarative reading: Procedural reading: H :- G1, G2, , Gn. “That H is provable follows from goals G1, G2, , Gn being provable.” “To execute procedure H, the procedures called by goals G1, G2, , Gn are executed first.”

male(bertram). male(percival). female(lucinda). female(camilla). pair(X, Y) :- male(X), female(Y). ?- pair(percival, X). ?- pair(apollo, daphne). ?- pair(camilla, X). ?- pair(X, lucinda). ?- pair(X, X). ?- pair(bertram, lucinda). ?- pair(X, daphne). ?- pair(X, Y).

Worksheet 2 drinks(john, martini). drinks(mary, gin). drinks(susan, vodka). drinks(john, gin). drinks(fred, gin). pair(X, Y, Z) :drinks(X, Z), drinks(Y, Z). ?- pair(X, john, martini). ?- pair(mary, susan, gin). ?- pair(john, mary, gin). ?- pair(john, john, gin). ?- pair(X, Y, gin). ?- pair(bertram, lucinda). ?- pair(bertram, lucinda, vodka). ?- pair(X, Y, Z). This definition forces X and Y to be distinct: pair(X, Y, Z) :- drinks(X, Z), drinks(Y, Z), X \ Y.

Worksheet 3 (a) Representing a symmetric relation. (b) Implementing a strange ticket condition. berkshire surrey kent wiltshire hampshire sussex How to represent this relation? Note that borders are symmetric.

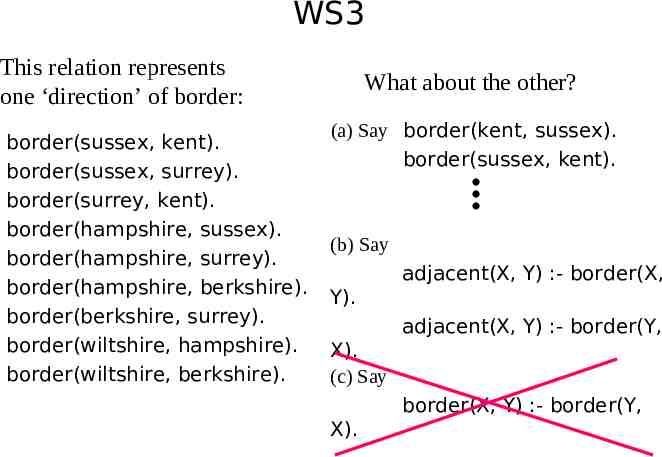
WS3 This relation represents one ‘direction’ of border: border(sussex, kent). border(sussex, surrey). border(surrey, kent). border(hampshire, sussex). border(hampshire, surrey). border(hampshire, berkshire). border(berkshire, surrey). border(wiltshire, hampshire). border(wiltshire, berkshire). What about the other? (a) Say border(kent, sussex). border(sussex, kent). (b) Say adjacent(X, Y) :- border(X, Y). adjacent(X, Y) :- border(Y, X). (c) Say border(X, Y) :- border(Y, X).

WS3 Now a somewhat strange type of discount ticket. For the ticket to be valid, one must pass through an intermediate county. A valid ticket between a start and end county obeys the following rule: valid(X, Y) :- adjacent(X, Z), adjacent(Z, Y)

WS3 border(sussex, kent). border(sussex, surrey). border(surrey, kent). border(hampshire, sussex). border(hampshire, surrey). border(hampshire, berkshire). border(berkshire, surrey). border(wiltshire, hampshire). border(wiltshire, berkshire). adjacent(X, Y) :- border(X, Y). adjacent(X, Y) :- border(Y, X). valid(X, Y) :adjacent(X, Z), adjacent(Z, Y) ?- valid(wiltshire, sussex). valid(wiltshire, kent). valid(hampshire, hampshire). valid(X, kent). valid(sussex, X). valid(X, Y).

Worksheet 4 arc a(g, h). a(g, d). a(e, d). a(h, f). a(e, f). a(a, e). a(a, b). a(b, f). a(b, c). a(f, c). a d Note that Prolog can distinguish between the 0-ary constant a (the name of a node) and the 2-ary functor a (the name of a relation). b e g c f h path(X, X). path(X, Y) :- a(X, Z), path(Z, Y). ?- path(f, f). path(a, c). path(g, e). path(g, X). path(X, h).

But what happens if a d b e g f h a(g, h). path(X, X). a(g, d). path(X, Y) :- a(X, Z), path(Z, Y). a(e, d). This program works c a(h, f). only for acyclic a(e, f). graphs. The program a(a, e). may infinitely loop a(a, b). given a cyclic graph. a(b, f). We need to leave a a(b, c). ‘trail’ of visited nodes. This is accomplished a(f, c). with a data structure a(d, a). (to be seen later).

Unification Two terms unify if substitutions can be made for any variables in the terms so that the terms are made identical. If no such substitution exists, the terms do not unify. The Unification Algorithm proceeds by recursive descent of the two terms. Constants unify if they are identical Variables unify with any term, including other variables Compound terms unify if their functors and components unify.

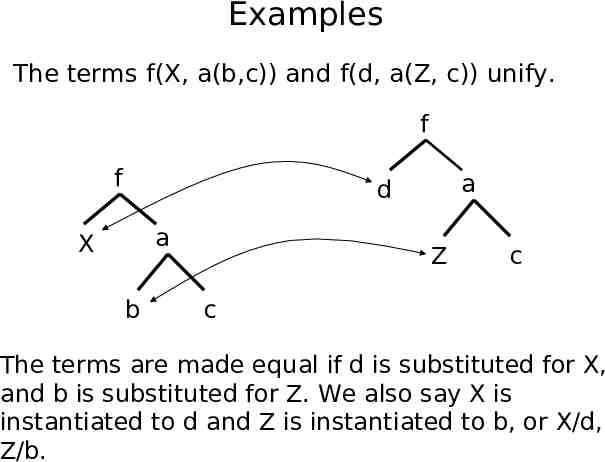
Examples The terms f(X, a(b,c)) and f(d, a(Z, c)) unify. f f a d a X b Z c c The terms are made equal if d is substituted for X, and b is substituted for Z. We also say X is instantiated to d and Z is instantiated to b, or X/d, Z/b.

Examples The terms f(X, a(b,c)) and f(Z, a(Z, c)) unify. f f a Z a X b Z c Note that Z co-refers within the term. Here, X/b, Z/b. c

Examples The terms f(c, a(b,c)) and f(Z, a(Z, c)) do not unify. f f a Z a c b Z c c No matter how hard you try, these two terms cannot be made identical by substituting terms for variables.

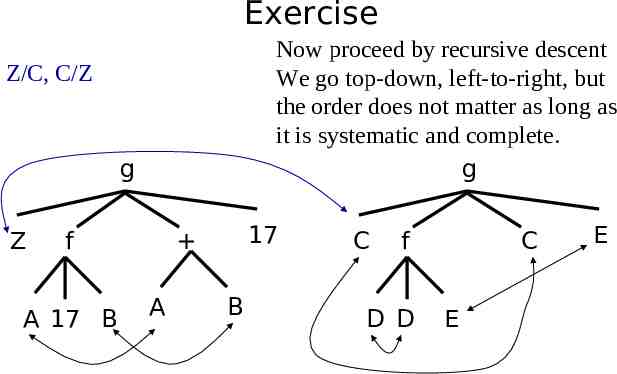
Exercise Do terms g(Z, f(A, 17, B), A B, 17) and g(C, f(D, D, E), C, E) unify? g Z g f A 17 B 17 A B C f D D C E E

Exercise First write in the co-referring variables. g Z g f A 17 B 17 A B C f D D C E E

Exercise Now proceed by recursive descent We go top-down, left-to-right, but the order does not matter as long as it is systematic and complete. g Z/C, C/Z g Z f A 17 B 17 A B C f D D C E E

Exercise Z/C, C/Z, A/D, D/A g Z g f A 17 B 17 A B C f D D C E E

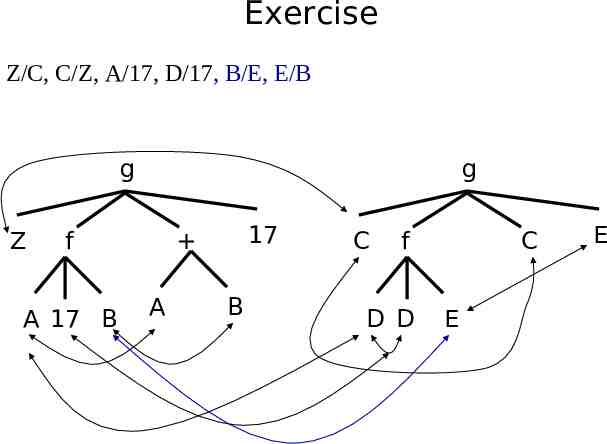
Exercise Z/C, C/Z, A/17, D/17 g Z g f A 17 B 17 A B C f D D C E E

Exercise Z/C, C/Z, A/17, D/17, B/E, E/B g Z g f A 17 B 17 A B C f D D C E E

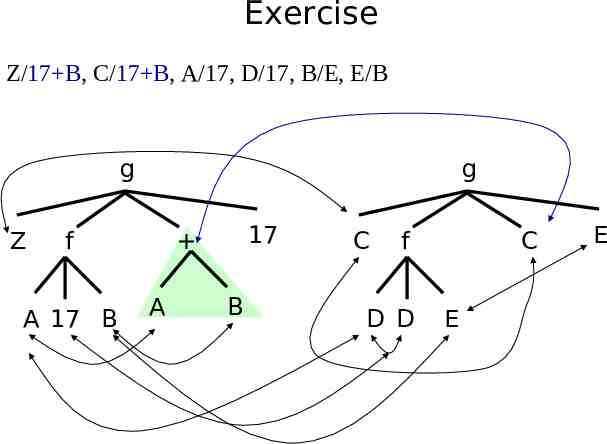
Exercise Z/17 B, C/17 B, A/17, D/17, B/E, E/B g Z g f A 17 B 17 A B C f D D C E E

Exercise Z/17 17, C/17 17, A/17, D/17, B/17, E/17 g Z g f A 17 B 17 A B C f D D C E E

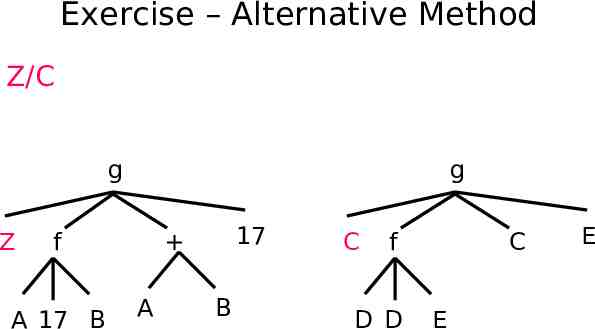
Exercise – Alternative Method Z/C g Z g f A 17 B 17 A B C f D D C E E

Exercise – Alternative Method Z/C g C g f A 17 B 17 A B C f D D C E E

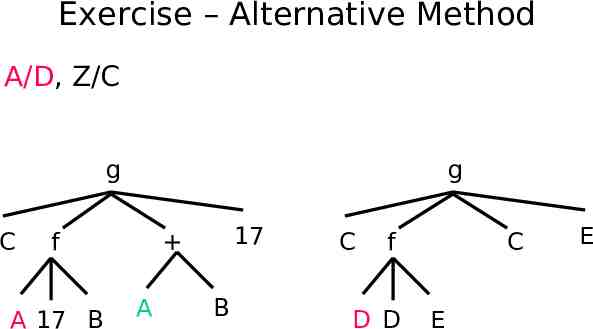
Exercise – Alternative Method A/D, Z/C g C g f A 17 B 17 A B C f D D C E E

Exercise – Alternative Method D/17, A/D, Z/C g C g f D 17 B 17 D B C f D D C E E

Exercise – Alternative Method D/17, A/17, Z/C g C f 17 17 B g 17 17 B C f 17 17 E C E

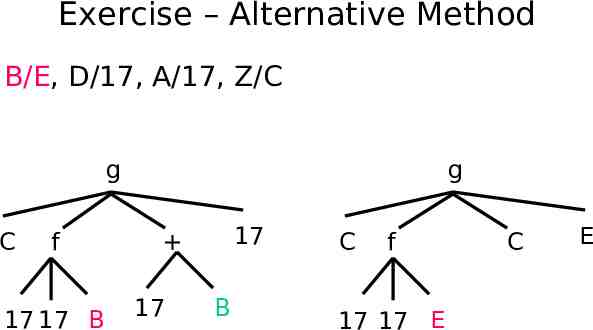
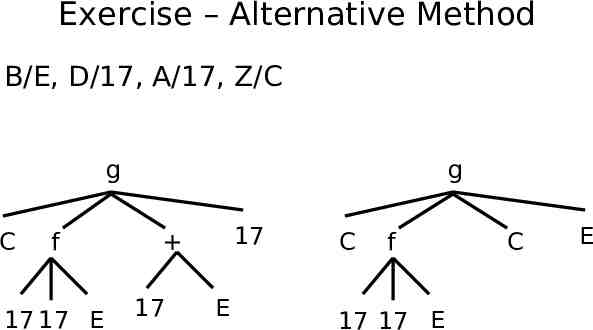
Exercise – Alternative Method B/E, D/17, A/17, Z/C g C f 17 17 B g 17 17 B C f 17 17 E C E

Exercise – Alternative Method B/E, D/17, A/17, Z/C g C f 17 17 E g 17 17 E C f 17 17 E C E

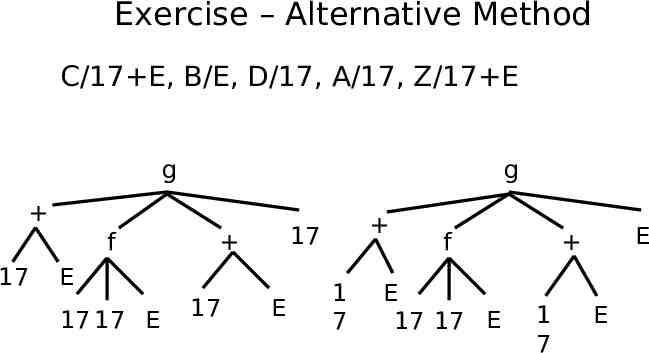
Exercise – Alternative Method C/17 E, B/E, D/17, A/17, Z/C g C f 17 17 E g 17 17 E C f 17 17 E C E

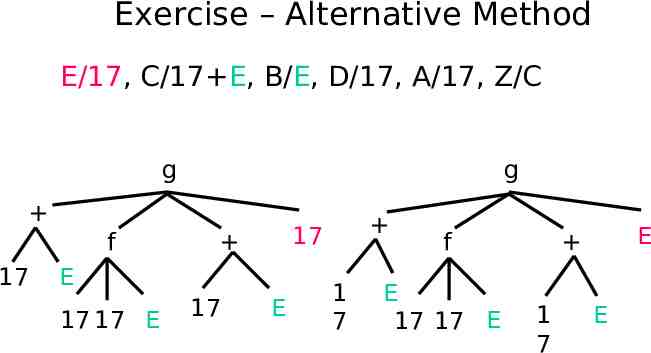
Exercise – Alternative Method C/17 E, B/E, D/17, A/17, Z/17 E g g f 17 E 17 17 E 17 17 E 1 7 f E 17 17 E E 1 7 E

Exercise – Alternative Method E/17, C/17 E, B/E, D/17, A/17, Z/C g g f 17 E 17 17 E 17 17 E 1 7 f E 17 17 E E 1 7 E

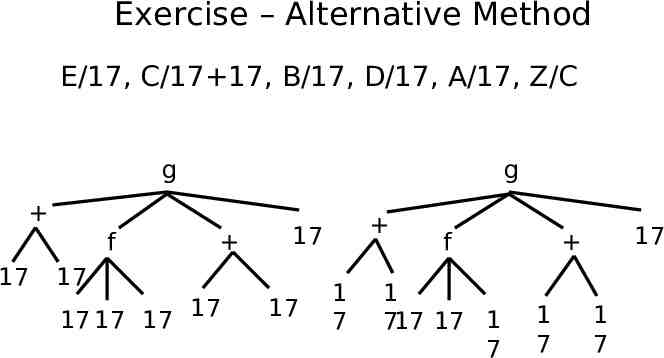
Exercise – Alternative Method E/17, C/17 17, B/17, D/17, A/17, Z/C g g f 17 17 17 17 17 17 17 17 1 7 f 1 717 17 1 7 17 1 7 1 7