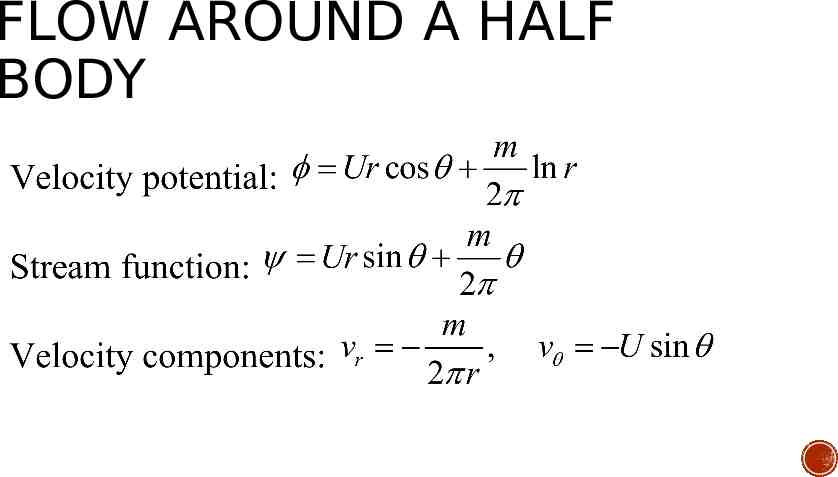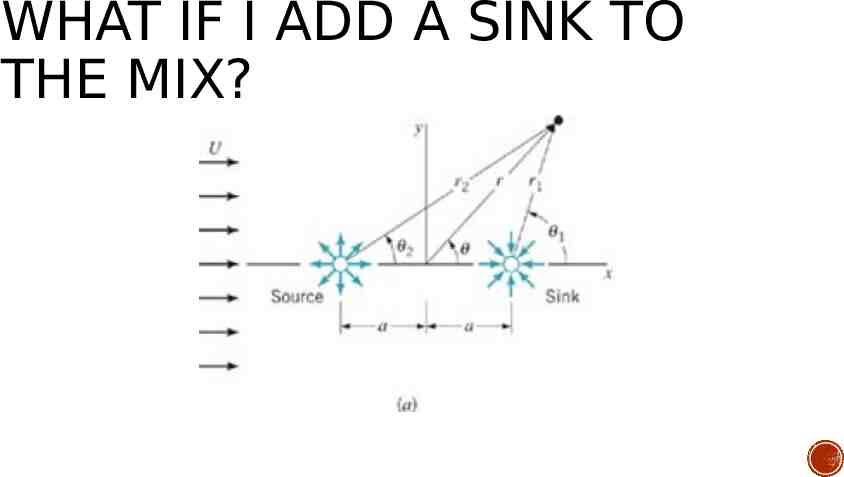POTENTIAL FLOW

POTENTIAL FLOW

POTENTIAL FLOW Assumptions Flow is inviscid Flow is irrotational Consequently – Beroulli’s equation is valid everywhere (i.e. not just between two points on a streamline) We can define a flow potential and a stream function f and y

GOVERNING EQUATIONS Flow potential and a stream function f and y. Same for streamfunction But on different grounds and only in 2d. See lectures for Chapter 6.

WHO CARES? These equations are linear So What? It means that we can use superposition to understand several simple flows, add them together and describe more complex flows. We can for example begin to understand why a a wing can generate lift and airplanes can fly even though in reality these also depend on viscous flows. But this is faster and simpler. But we need to understand some fundamental flows first.

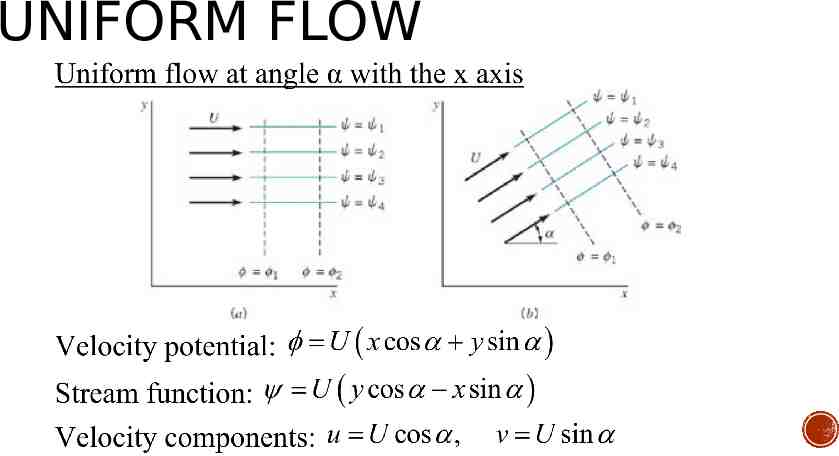
UNIFORM FLOW

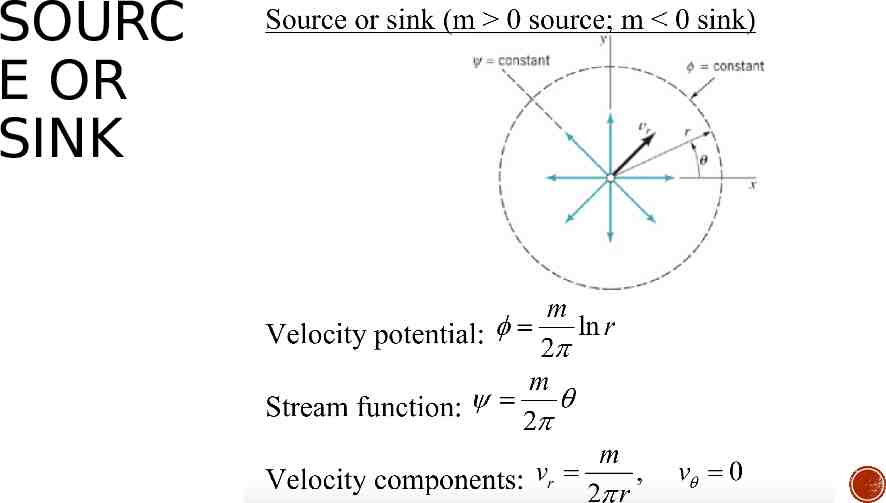
SOURC E OR SINK

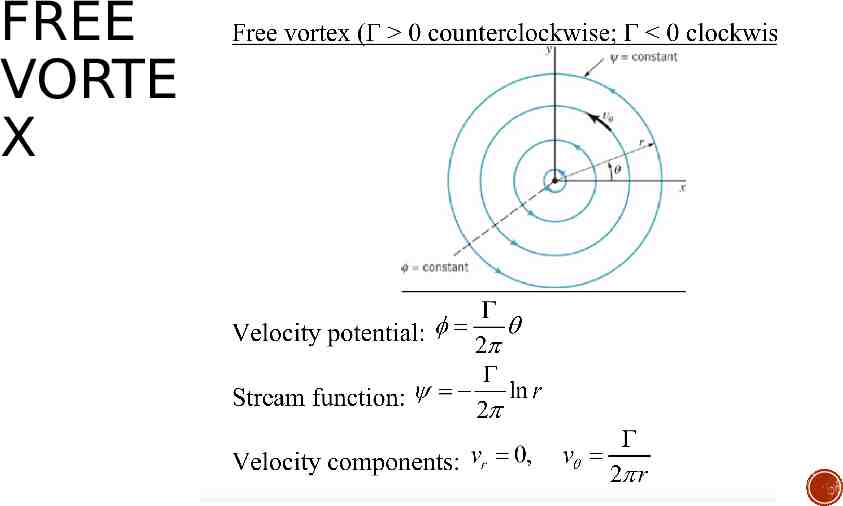
FREE VORTE X

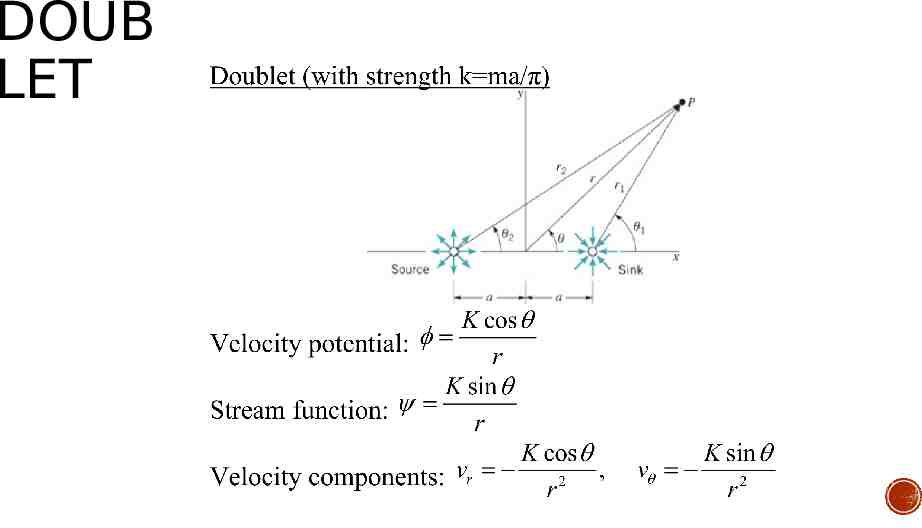
DOUB LET

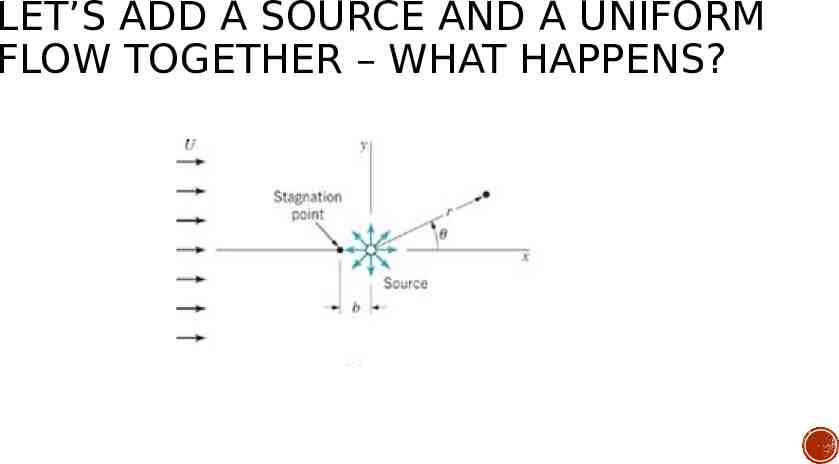
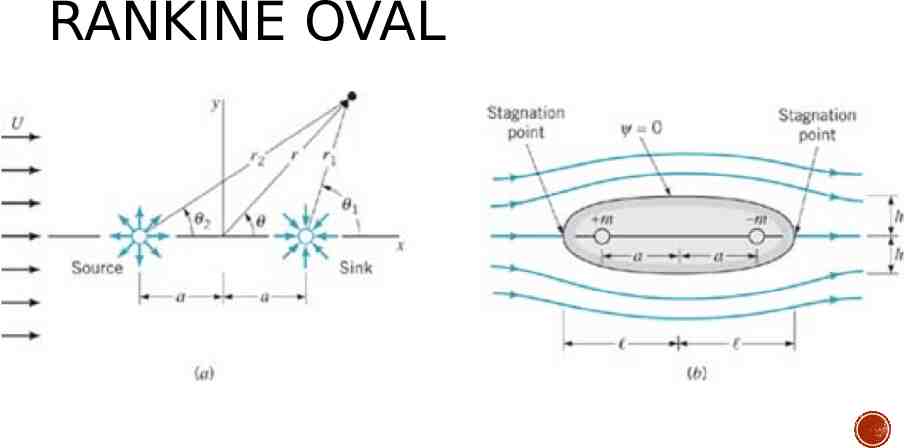
LET’S ADD A SOURCE AND A UNIFORM FLOW TOGETHER – WHAT HAPPENS?

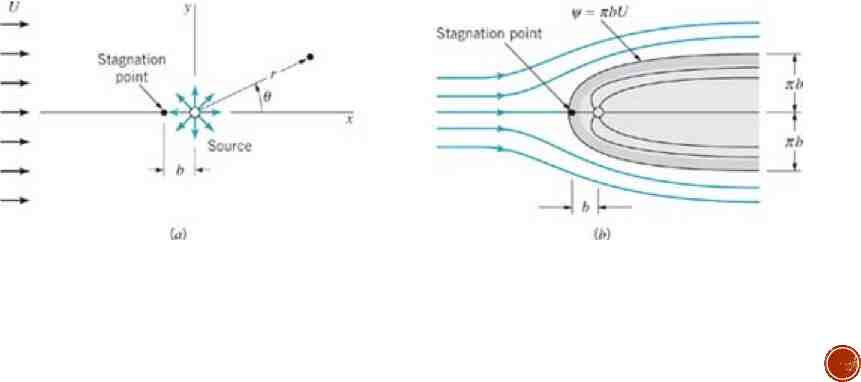
FLOW AROUND A HALF BODY

WHAT IF I ADD A SINK TO THE MIX?

RANKINE OVAL

RANKINE OVAL

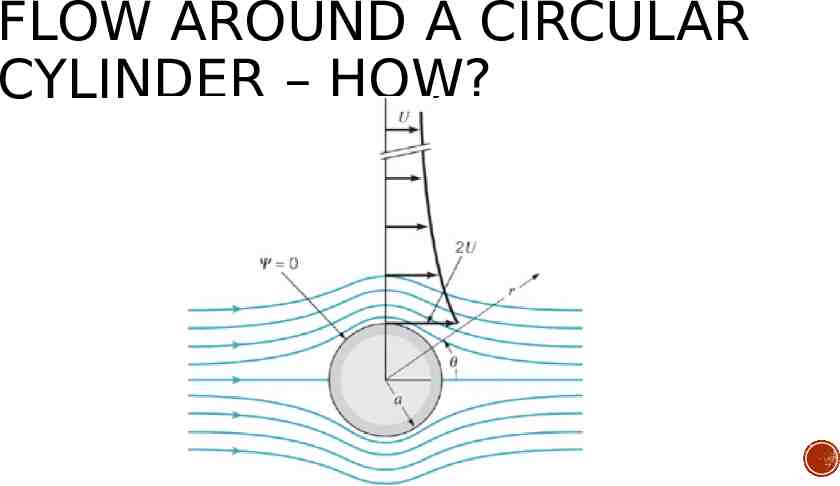
FLOW AROUND A CIRCULAR CYLINDER – HOW?

FLOW AROUND A CIRCULAR CYLINDER A doublet combined with a uniform flow can be used to represent flow around a circular cylinder.

QUESTION: WHAT IS THE LIFT ON THE SPHERE?

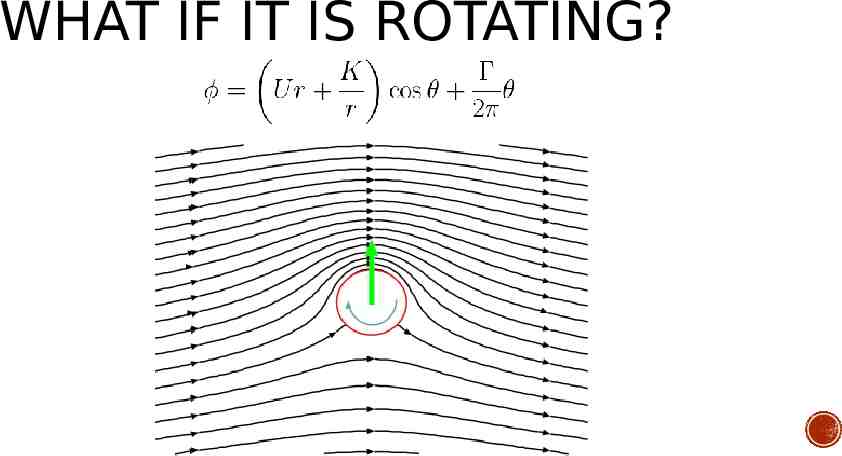
WHAT IF IT IS ROTATING?

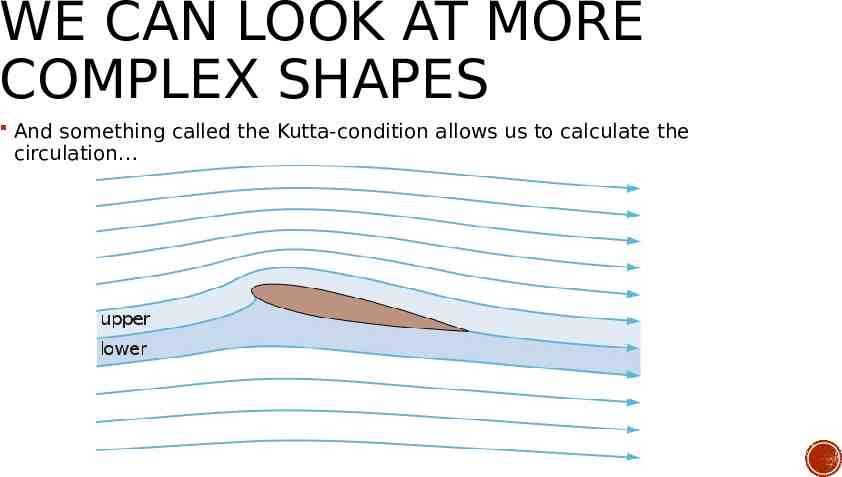
WE CAN LOOK AT MORE COMPLEX SHAPES And something called the Kutta-condition allows us to calculate the circulation

SAMPLE PROBLEMS