Physics 10 UCSD Quantum Mechanics Small things are weird
19 Slides694.00 KB
Physics 10 UCSD Quantum Mechanics Small things are weird
Physics 10 UCSD The Quantum Mechanics View All matter (particles) has wave-like properties – so-called particle-wave duality Particle-waves are described in a probabilistic manner – electron doesn’t whiz around the nucleus, it has a probability distribution describing where it might be found – allows for seemingly impossible “quantum tunneling” Some properties come in dual packages: can’t know both simultaneously to arbitrary precision – called the Heisenberg Uncertainty Principle – not simply a matter of measurement precision – position/momentum and energy/time are example pairs The act of “measurement” fundamentally alters the system – called entanglement: information exchange alters a particle’s state Spring 2008 2
Physics 10 UCSD Crises in physics that demanded Q.M. Why don’t atoms disintegrate in nanoseconds? – if electron is “orbiting”, it’s accelerating (wiggling) – wiggling charges emit electromagnetic radiation (energy) – loss of energy would cause prompt decay of orbit Why don’t hot objects emit more ultraviolet light than they do? – classical theory suggested a “UV catastrophe,” leading to obviously nonsensical infinite energy radiating from hot body – Max Planck solved this problem by postulating light quanta (now often called the father of quantum mechanics) Spring 2008 3
Physics 10 UCSD Pre-quantum problems, cont. Why was red light incapable of knocking electrons out of certain materials, no matter how bright – yet blue light could readily do so even at modest intensities – called the photoelectric effect – Einstein explained in terms of photons, and won Nobel Prize Spring 2008 4
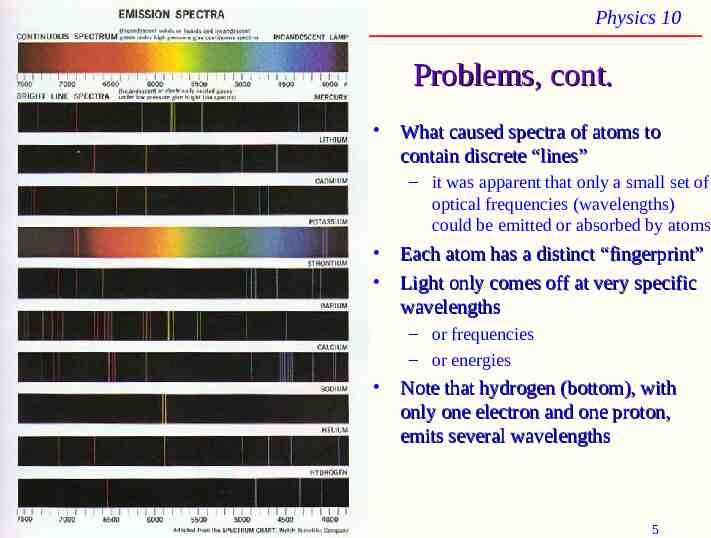
Physics 10 UCSD Problems, cont. What caused spectra of atoms to contain discrete “lines” – it was apparent that only a small set of optical frequencies (wavelengths) could be emitted or absorbed by atoms Each atom has a distinct “fingerprint” Light only comes off at very specific wavelengths – or frequencies – or energies Note that hydrogen (bottom), with only one electron and one proton, emits several wavelengths Spring 2008 5
Physics 10 UCSD The victory of the weird theory Without Quantum Mechanics, we could never have designed and built: – semiconductor devices computers, cell phones, etc. – lasers CD/DVD players, bar-code scanners, surgical applications – MRI (magnetic resonance imaging) technology – nuclear reactors – atomic clocks (e.g., GPS navigation) Physicists didn’t embrace quantum mechanics because it was gnarly, novel, or weird – it’s simply that the # !&@ thing worked so well Spring 2008 6
Physics 10 UCSD Let’s start with photon energy Light is quantized into packets called photons Photons have associated: – – – – frequency, (nu) wavelength, ( c) speed, c (always) energy: E h higher frequency photons higher energy more damaging – momentum: p h /c The constant, h, is Planck’s constant – has tiny value of: h 6.63 10-34 J·s Spring 2008 7
Physics 10 UCSD How come I’ve never seen a photon? Sunny day (outdoors): – 1015 photons per second enter eye (2 mm pupil) Moonlit night (outdoors): – 5 1010 photons/sec (6 mm pupil) Moonless night (clear, starry sky) – 108 photons/sec (6 mm pupil) Light from dimmest naked eye star (mag 6.5): – 1000 photons/sec entering eye – integration time of eye is about 1/8 sec 100 photon threshold signal level Spring 2008 8
Physics 10 UCSD Quantum Wavelength Every particle or system of particles can be defined in quantum mechanical terms – and therefore have wave-like properties The quantum wavelength of an object is: h/p – called the de Broglie wavelength (p is momentum) typical macroscopic objects – masses kg; velocities m/s p 1 kg·m/s 10-34 meters (too small to matter in macro environment!!) typical “quantum” objects: – electron (10-30 kg) at thermal velocity (105 m/s) 10-8 m – so is 100 times larger than an atom: very relevant to an electron! Spring 2008 9
Physics 10 UCSD The Uncertainty Principle The process of measurement involves interaction – this interaction necessarily “touches” the subject – by “touch,” we could mean by a photon of light The more precisely we want to know where something is, the “harder” we have to measure it – so we end up giving it a kick So we must unavoidably alter the velocity of the particle under study – thus changing its momentum If x is the position uncertainty, and p is the momentum uncertainty, then inevitably, x p h/2 Spring 2008 10
Physics 10 UCSD Example: Diffraction Light emerging from a tiny hole or slit will diverge (diffract) We know its position very well (in at least one dimension) – so we give up knowledge of momentum in that dimension—thus the spread large opening: greater position uncertainty results in smaller momentum uncertainty, which translates to less of a spread angle small opening: less position uncertainty results in larger momentum uncertainty, which translates to more of a spread angle angle p/p h/p x h /h x / x Spring 2008 11
Physics 10 UCSD Diffraction in Our Everyday World Squint and things get fuzzy – opposite behavior from particle-based pinhole camera Eye floaters – look at bright, uniform source through tiniest pinhole you can make—you’ll see slowly moving specks with rings around them—diffraction rings Shadow between thumb and forefinger – appears to connect before actual touch Streaked street-lights through windshield – point toward center of wiper arc: diffraction grating formed by micro-grooves in windshield from wipers – same as color/streaks off CD Spring 2008 12
Physics 10 UCSD The Double Slit Experiment particle? Spring 2008 wave? 13
Physics 10 UCSD Results The pattern on the screen is an interference pattern characteristic of waves So light is a wave, not particulate But repeat the experiment one photon at a time Over time, the photons only land on the interference peaks, not in the troughs – consider the fact that they also pile up in the middle! – pure ballistic particles would land in one of two spots Spring 2008 14
UCSD Physics 10 Wave or Particle? Neither; Both; take your pick Non-intuitive combination of wavelike and particle-like Appears to behave in wavelike manner. But with low intensity, see the interference pattern build up out of individual photons, arriving one at a time. How does the photon know about “the other” slit? – Actually, it’s impossible to simultaneously observe interference and know which slit the photon came through – Photon “sees”, or “feels-out” both paths simultaneously! Speak of wave-part describing probability distribution of where individual photons may land Spring 2008 15
Physics 10 UCSD The hydrogen atom When the mathematical machinery of quantum mechanics is turned to the hydrogen atom, the solutions yield energy levels in exact agreement with the optical spectrum – Emergent picture is one of probability distributions describing where electrons can be The energy levels of hydrogen match the observed spectra, and fall out of the mathematics of quantum mechanics Probability distributions are static – electron is not thought to whiz around atom: it’s in a “stationary state” of probability Separate functions describe the radial and angular pattern – http://hyperphysics.phy-astr.gsu.edu/hbase/hydwf.html Spring 2008 16
Physics 10 UCSD The angular part of the story These plots describe the directions in which one is likely to find an electron. They are denoted with quantum numbers l and m, with l as the subscript and m as the superscript. s p The s state (l 0,m 0) is spherically symmetric: equal probability of finding in all directions. d The p state can be most likely to find at the poles (and not at all at the equator) in the case of (1,0), and exactly the opposite situation in the (1,1) state. f Spring 2008 17
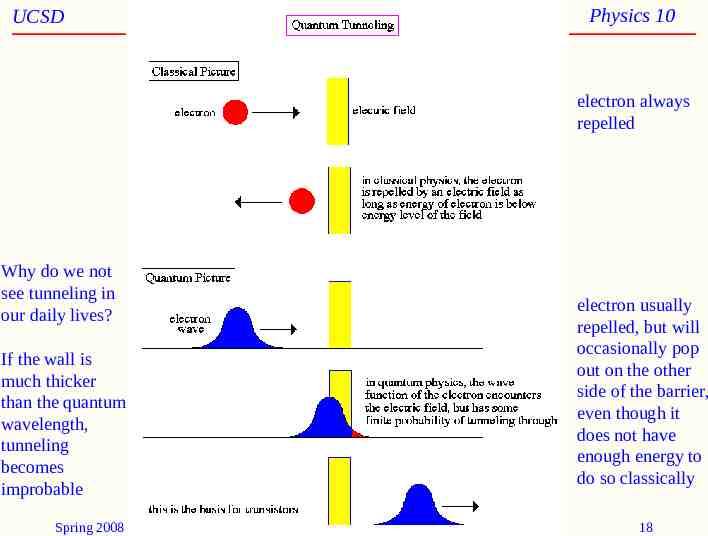
UCSD Physics 10 electron always repelled Why do we not see tunneling in our daily lives? If the wall is much thicker than the quantum wavelength, tunneling becomes improbable Spring 2008 electron usually repelled, but will occasionally pop out on the other side of the barrier, even though it does not have enough energy to do so classically 18
Physics 10 UCSD Assignments References: – Brian Greene’s The Elegant Universe has an excellent description/analogy of the quantum solution to the ultraviolet catastrophe (among other quantum things) – Chapter 31 isn’t half bad: read it for fun, even! Assignments: – Read Hewitt chapters 30 & 31 (Quantum & Light) – Read Hewitt pp. 566–572 on diffraction & interference – HW 7 due 5/30: 26.E.3, 26.E.4, 26.E.10, 26.E.14, 26.E.38, 26.P.4, 31.E.4, 31.E.9, plus 4 additional questions available from website Spring 2008 19