Pattern Analysis Prof. Bennett Math Model of Learning and Discovery

Pattern Analysis Prof. Bennett Math Model of Learning and Discovery 2/14/05 Based on Chapter 1 of Shawe-Taylor and Cristianini

Outline What is pattern analysis? Illustrate issues via example Pattern definitions Examples of practical tasks Pattern algorithms Summary

Pattern Analysis The automatic detection of patterns in data from the same source. Make predictions of new data coming from the same source. Data may take many forms: images, text, records of commercial transactions, genome sequences, family tree

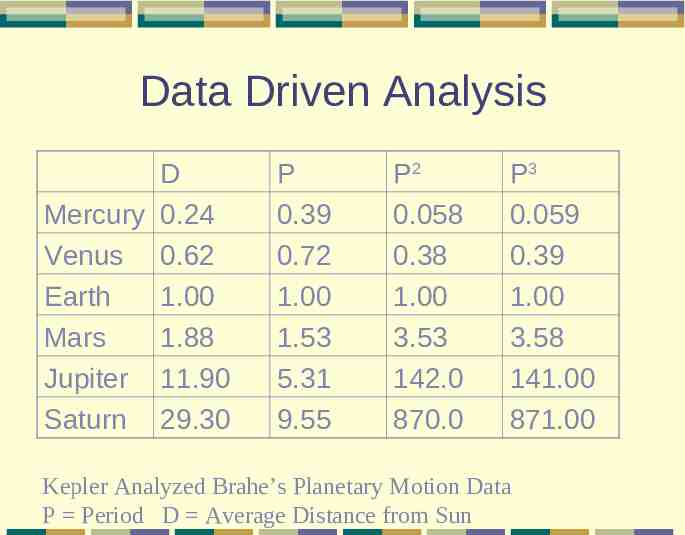
Data Driven Analysis D Mercury 0.24 Venus 0.62 Earth 1.00 Mars 1.88 Jupiter 11.90 Saturn 29.30 P 0.39 0.72 1.00 1.53 5.31 9.55 P2 0.058 0.38 1.00 3.53 142.0 870.0 P3 0.059 0.39 1.00 3.58 141.00 871.00 Kepler Analyzed Brahe’s Planetary Motion Data P Period D Average Distance from Sun

Found “Regularities” Observed P3 D2 Developed three laws of planetary motion. Compressible: Data can be represented by one column Predictable: Discovering hidden relations allow us to predict other columns. Third Law is exact.

Data Representation I Nonlinear Model of D and P 2 3 D P 0 2 3 ˆ ˆ Linear Model of D D and P P 2 3 ˆ ˆ D P D P 0

Data Representation II Assume we know plane of orbit, so we can represent positions as (x,y) pairs Also know orbit is ellipse 2 2 c1 x c2 y c3 xy c4 x c5 y c6 0

Data Representation 2 2 c1 x c2 y c3 xy c4 x c5 y c6 0 Pattern is nonlinear function of x,y 2 2 Pattern is linear function of x , y , xy , x, y Linear relationships are easier to find.

Set of Hypotheses 2 2 c1 x c2 y c3 xy c4 x c5 y c6 0 Hypothesis Ellipse compute c1 , c2 , c3 , c4 , c5 , c6 Hypothesis Circle compute c1 , c2 , c6 UNDERFITS

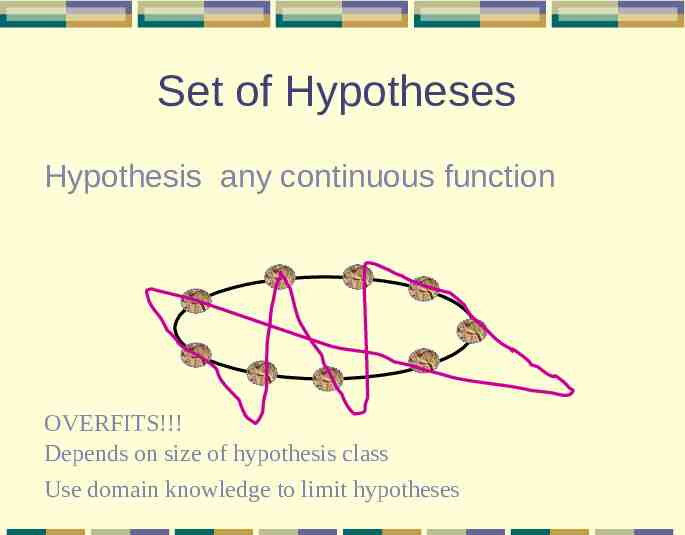
Set of Hypotheses Hypothesis any continuous function OVERFITS!!! Depends on size of hypothesis class Use domain knowledge to limit hypotheses

Approximate Pattern Noisy Data

Typical Pattern Analysis Approximate not exact. Data has errors and omissions. Cannot predict graduate school performance from GRE’s and grades alone. Best Representation/Model unknown. Make approximate predictions – need to address how accurate estimates are.

Definition: Exact Pattern A general exact pattern, f, for data source S satisfies f ( x) 0 for all data x from source S

Approximate Pattern A general approximate pattern, f, for data source S satisfies f ( x) 0 for all data x from source S

Statistical Pattern A general statistical pattern, f, for data source S generated iid according to distribution D satisfies ED f ( x) Ex f ( x) 0 for all data x from source S

Two and Multiclass Classification Example – Character Recognition two class - is it an A or not? multiclass – what letter is it ? f (z ) L( y, g ( x)) 0 g is prediction function L is loss function y { 1,1} or y {1, 2,3, 4,., N }

Regression Example –Determine drug bioavailability through the intestine. Estimate apparent permeability as assayed via intestinal cell line. f (z ) L( y, g (x)) 0 g is prediction function L is loss function y R

Density Estimation Estimate the probability that a particular event occurs, p(x). Use it to detect improbably events like fraud. f ( x) 0 f(x)dx 1 x E ( ln( f ( x)) E ( ln( p ( x)) 0 Kullback-Lieber divergence

Principal Component Analysis Find a projection of the data that captures the major variance in the data. Eigenfaces - capture essential qualities of faces to help ID and reduce storage needs. Projection PV : X V Residual f ( x) PV ( x) x 2 Minimize expected value of residual

Pattern Analysis Algorithm A Pattern Analysis Algorithm input finite set of data from source S a.k.a. the training set output detector function f or no patterns detected

Pattern Algorithm Issues Efficiency and Scalability – memory and CPU requirements, large data sets Robustness – find approximate patterns on noisy data Stability - discover genuine patterns, find same problems on different views of the dataset

Stability Generalization – Find pattern on future data Pattern may exist by chance for finite sample Provide statistical guarantee that pattern truly exist with caveat that with small probability that algorithm may have been mislead.

Example Observe that for state agency that all 20 babies adopted in last 10 years from country x are girls. Pattern, only girls are available for adoption from that country. With probability p (0.5)220 could observe data even if chance of girls and boys equally likely. So with chance p, we were mislead.

Statistical Learning Theory Produce a pattern based on a finite sample. Provide bounds on the probability that pattern approximately represents a true pattern with some probability. Probably Approximately Correct

Recoding Strategy With proper representation, the problem can become easier (linear model works). Develop general purpose linear learning methods. Change recoding using “kernel functions”

Key Ideas Patterns are regularities in data from a specified source Algorithm takes finite sample and computes pattern Efficiency, robustness, and stability Representation -- Kernels Strategy Generic Algorithms Recoding Many Learning Tasks in this framework