Parallel Lines & Transversals Geometry

Parallel Lines & Transversals Geometry

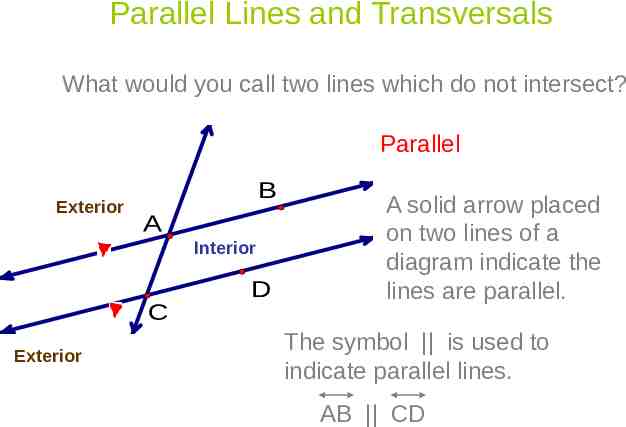
Parallel Lines and Transversals What would you call two lines which do not intersect? Parallel Exterior B A Interior C Exterior D A solid arrow placed on two lines of a diagram indicate the lines are parallel. The symbol is used to indicate parallel lines. AB CD

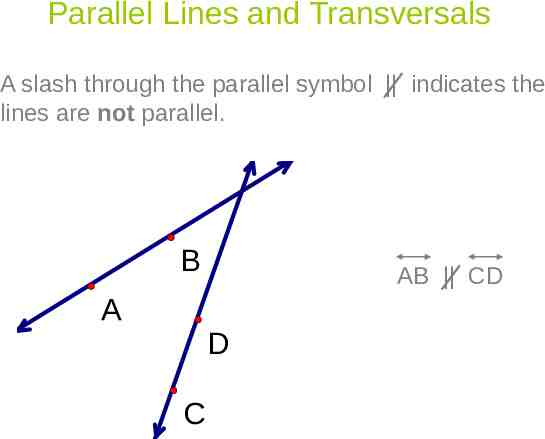
Parallel Lines and Transversals A slash through the parallel symbol indicates the lines are not parallel. B A AB CD D C

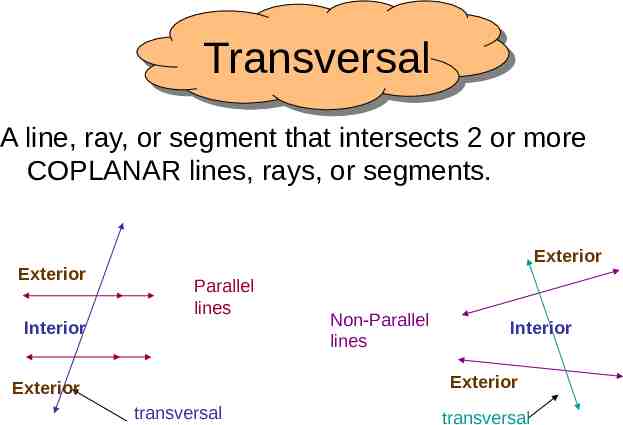
Transversal A line, ray, or segment that intersects 2 or more COPLANAR lines, rays, or segments. Exterior Exterior Parallel lines Interior Non-Parallel lines Interior Exterior Exterior transversal transversal

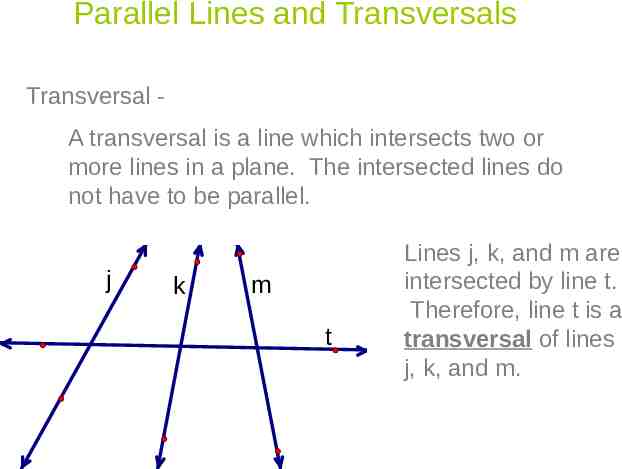
Parallel Lines and Transversals Transversal A transversal is a line which intersects two or more lines in a plane. The intersected lines do not have to be parallel. j k m t Lines j, k, and m are intersected by line t. Therefore, line t is a transversal of lines j, k, and m.

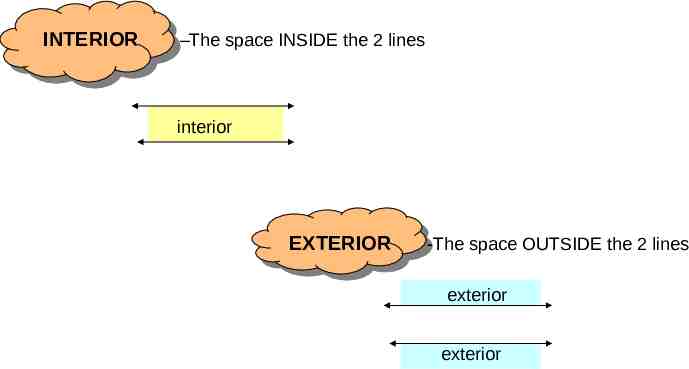
INTERIOR –The space INSIDE the 2 lines interior EXTERIOR -The space OUTSIDE the 2 lines exterior exterior

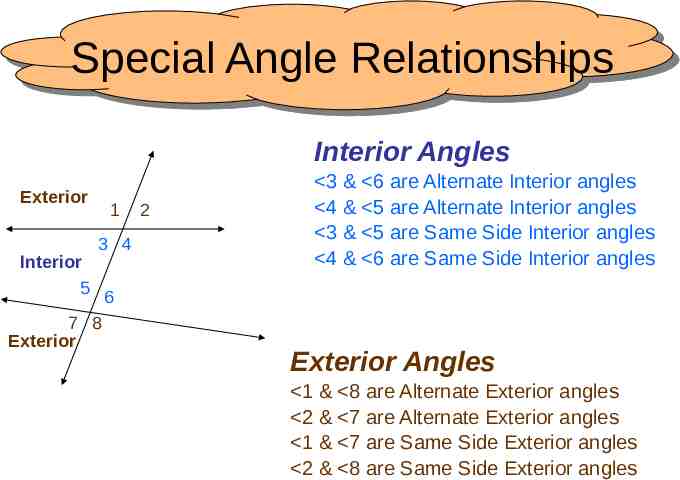
Special Angle Relationships Interior Angles Exterior 1 3 4 Interior 5 6 7 8 Exterior 2 3 & 6 are Alternate Interior angles 4 & 5 are Alternate Interior angles 3 & 5 are Same Side Interior angles 4 & 6 are Same Side Interior angles Exterior Angles 1 & 8 are Alternate Exterior angles 2 & 7 are Alternate Exterior angles 1 & 7 are Same Side Exterior angles 2 & 8 are Same Side Exterior angles

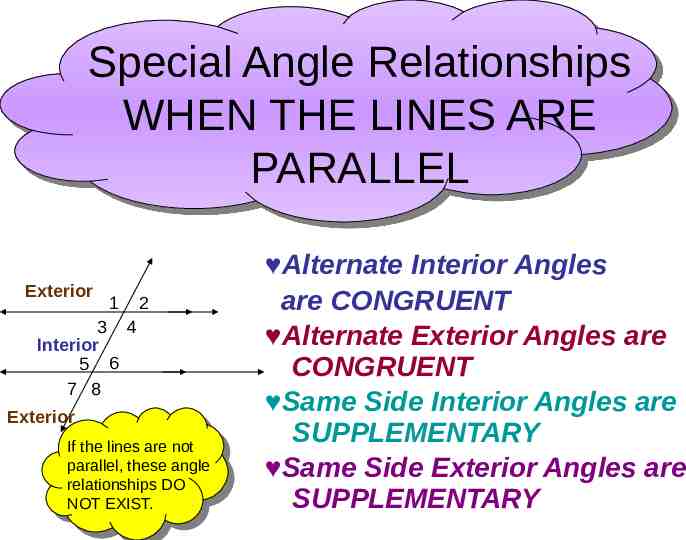
Special Angle Relationships WHEN THE LINES ARE PARALLEL Exterior 1 2 3 4 Interior 5 6 7 8 Exterior If the lines are not parallel, these angle relationships DO NOT EXIST. Alternate Interior Angles are CONGRUENT Alternate Exterior Angles are CONGRUENT Same Side Interior Angles are SUPPLEMENTARY Same Side Exterior Angles are SUPPLEMENTARY

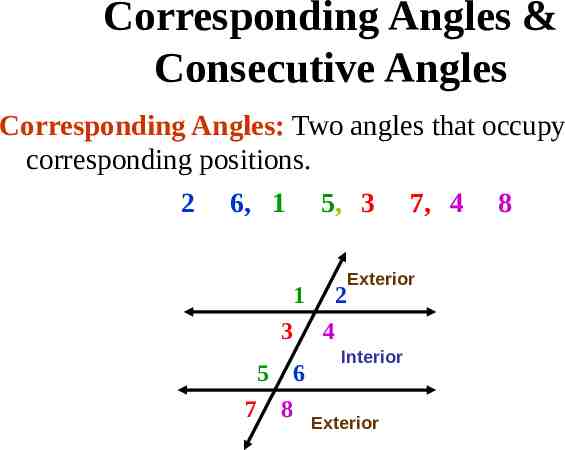
Corresponding Angles & Consecutive Angles Corresponding Angles: Two angles that occupy corresponding positions. 2 6, 1 5, 3 7, 4 8 1 3 2 4 Exterior Interior 5 6 7 8 Exterior

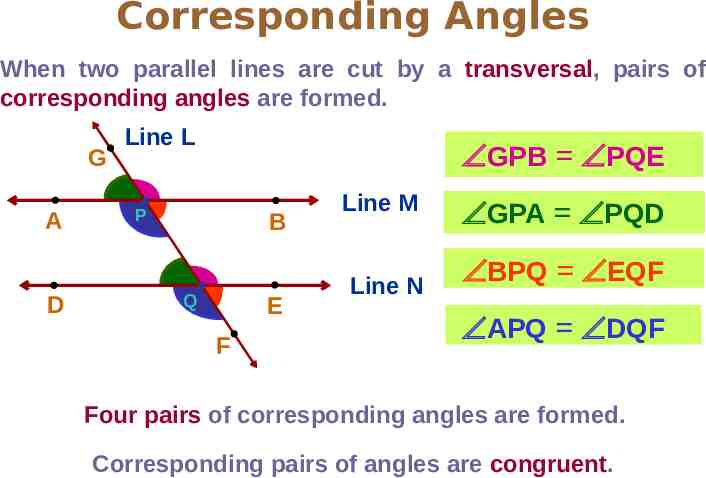
Corresponding Angles When two parallel lines are cut by a transversal, pairs of corresponding angles are formed. L Line L ÐGPB ÐPQE G A D P B Q E F Line M Line N ÐGPA ÐPQD ÐBPQ ÐEQF ÐAPQ ÐDQF Four pairs of corresponding angles are formed. Corresponding pairs of angles are congruent.

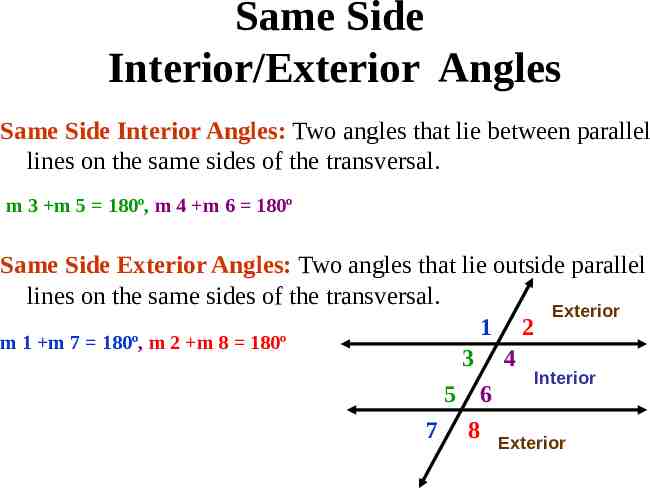
Same Side Interior/Exterior Angles Same Side Interior Angles: Two angles that lie between parallel lines on the same sides of the transversal. m 3 m 5 180º, m 4 m 6 180º Same Side Exterior Angles: Two angles that lie outside parallel lines on the same sides of the transversal. Exterior 1 2 m 1 m 7 180º, m 2 m 8 180º 3 4 Interior 5 6 7 8 Exterior

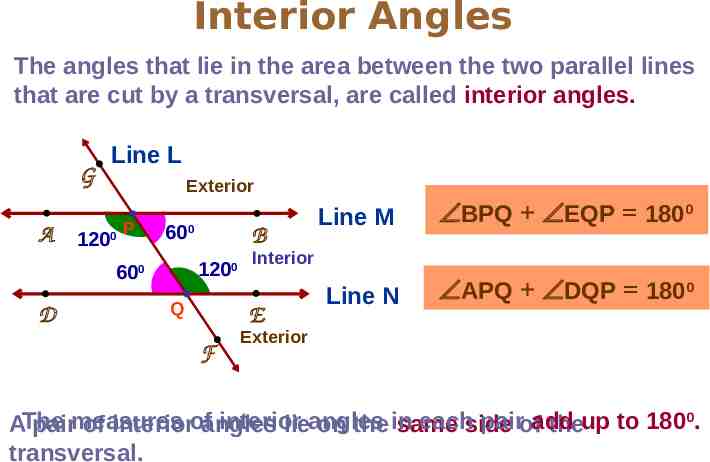
Interior Angles The angles that lie in the area between the two parallel lines that are cut by a transversal, are called interior angles. L G Line L Exterior A 1200 P 60 D 600 B 1200 0 Q ÐBPQ ÐEQP 1800 Line N ÐAPQ ÐDQP 1800 Interior E F Line M Exterior interior eachside pairofadd AThe pairmeasures of interiorofangles lieangles on the in same theup to 1800. transversal.

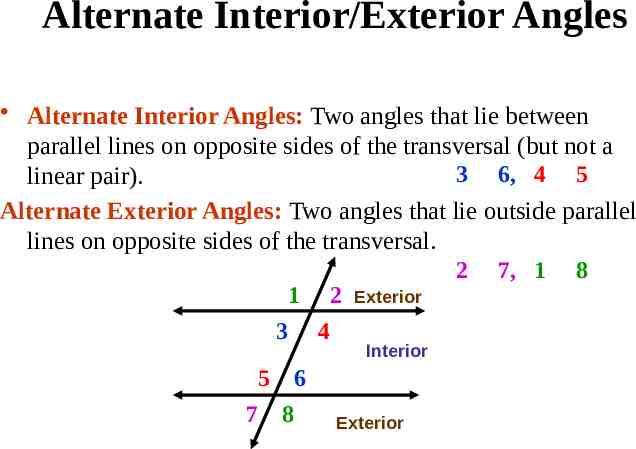
Alternate Interior/Exterior Angles Alternate Interior Angles: Two angles that lie between parallel lines on opposite sides of the transversal (but not a 3 6, 4 5 linear pair). Alternate Exterior Angles: Two angles that lie outside parallel lines on opposite sides of the transversal. 2 7, 1 8 1 2 Exterior 3 4 Interior 5 6 7 8 Exterior

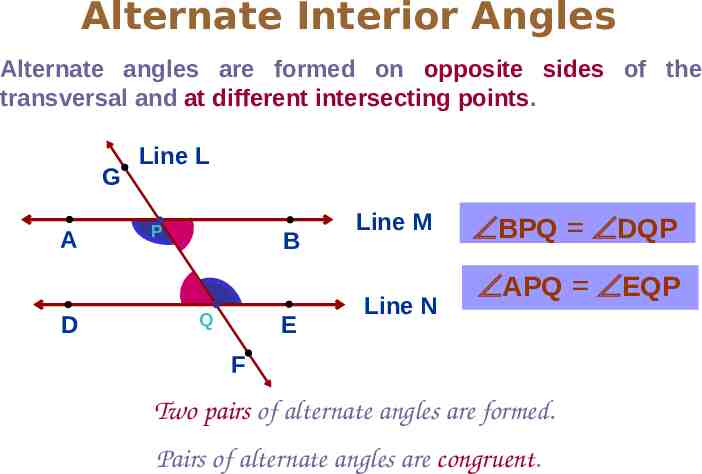
Alternate Interior Angles Alternate angles are formed on opposite sides of the transversal and at different intersecting points. L A D G Line L P B Q E Line M Line N ÐBPQ ÐDQP ÐAPQ ÐEQP F Two pairs of alternate angles are formed. Pairs of alternate angles are congruent.

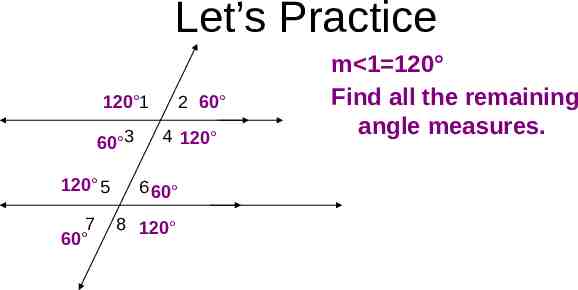
Let’s Practice 120 1 60 3 120 5 7 60 2 60 4 120 6 60 8 120 m 1 120 Find all the remaining angle measures.

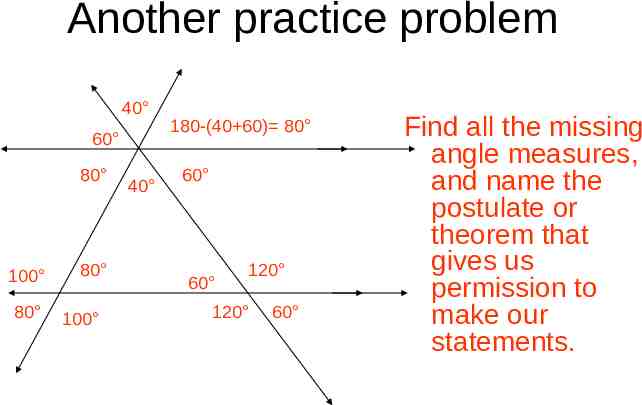
Another practice problem 40 60 80 100 80 80 100 40 180-(40 60) 80 60 60 120 120 60 Find all the missing angle measures, and name the postulate or theorem that gives us permission to make our statements.