Optimizing Bandwidth Limited Problems Using One-Sided

Optimizing Bandwidth Limited Problems Using One-Sided Communication and Overlap Christian Bell1,2, Dan Bonachea1, Rajesh Nishtala1, and Katherine Yelick1,2 1 UC Berkeley, Computer Science Division 2 Lawrence Berkeley National Laboratory Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 1

Conventional Wisdom Send few, large messages – Allows the network to deliver the most effective bandwidth Isolate computation and communication phases – Uses bulk-synchronous programming – Allows for packing to maximize message size Message passing is preferred paradigm for clusters Global Address Space (GAS) Languages are primarily useful for latency sensitive applications GAS Languages mainly help productivity – However, not well known for their performance advantages Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 2

Our Contributions Increasingly, cost of HPC machines is in the network One-sided communication model is a better match to modern networks – GAS Languages simplify programming for this model How to use these communication advantages – Case study with NAS Fourier Transform (FT) – Algorithms designed to relieve communication bottlenecks Overlap communication and computation Send messages early and often to maximize overlap Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 3

UPC Programming Model Global address space: any thread/process may directly read/write data allocated by another Partitioned: data is designated as local (near) or global (possibly far); programmer controls layout shared g: g: l: l: Proc 0 Proc 1 private g: l: Global arrays: Allows any processor to directly access data on any other processor Proc n-1 3 of the current languages: UPC, CAF, and Titanium – Emphasis in this talk on UPC (based on C) – However programming paradigms presented in this work are not limited to UPC Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 4

Advantages of GAS Languages Productivity – GAS supports construction of complex shared data structures – High level constructs simplify parallel programming – Related work has already focused on these advantages Performance (the main focus of this talk) – GAS Languages can be faster than two-sided MPI – One-sided communication paradigm for GAS languages more natural fit to modern cluster networks – Enables novel algorithms to leverage the power of these networks – GASNet, the communication system in the Berkeley UPC Project, is designed to take advantage of this communication paradigm Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 5

One-Sided vs Two-Sided one-sided put (e.g., GASNet) dest. addr. data payload two-sided message (e.g., MPI) message id network interface host CPU memory data payload A one-sided put/get can be entirely handled by network interface with RDMA support – CPU can dedicate more time to computation rather than handling communication A two-sided message can employ RDMA for only part of the communication – Each message requires the target to provide the destination address – Offloaded to network interface in networks like Quadrics RDMA makes it apparent that MPI has added costs associated with ordering to make it usable as a end-user programming model Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 6

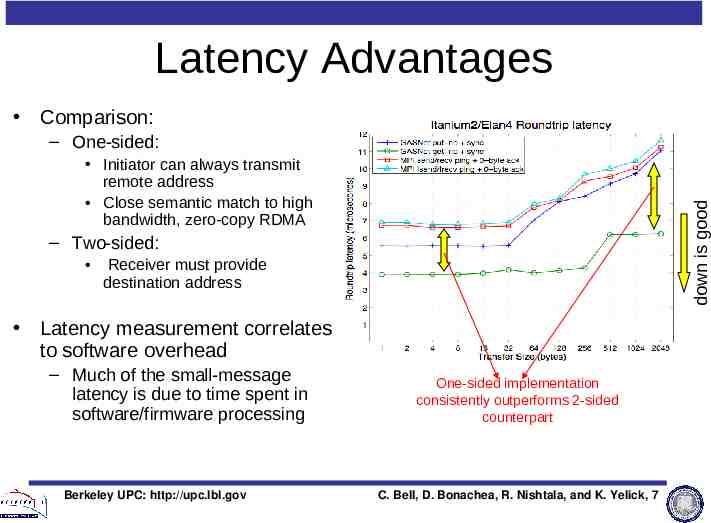
Latency Advantages Comparison: – One-sided: down is good Initiator can always transmit remote address Close semantic match to high bandwidth, zero-copy RDMA – Two-sided: Receiver must provide destination address Latency measurement correlates to software overhead – Much of the small-message latency is due to time spent in software/firmware processing Berkeley UPC: http://upc.lbl.gov One-sided implementation consistently outperforms 2-sided counterpart C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 7

Bandwidth Advantages One-sided semantics better match to RDMA supported networks up is good – Relaxing point-to-point ordering constraint can allow for higher performance on some networks – GASNet saturates to hardware peak at lower message sizes – Synchronization decoupled from data transfer MPI semantics designed for end user – Comparison against good MPI implementation – Semantic requirements hinder MPI performance – Synchronization and data transferred coupled together in message passing Berkeley UPC: http://upc.lbl.gov Over a factor of 2 improvement for 1kB messages C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 8

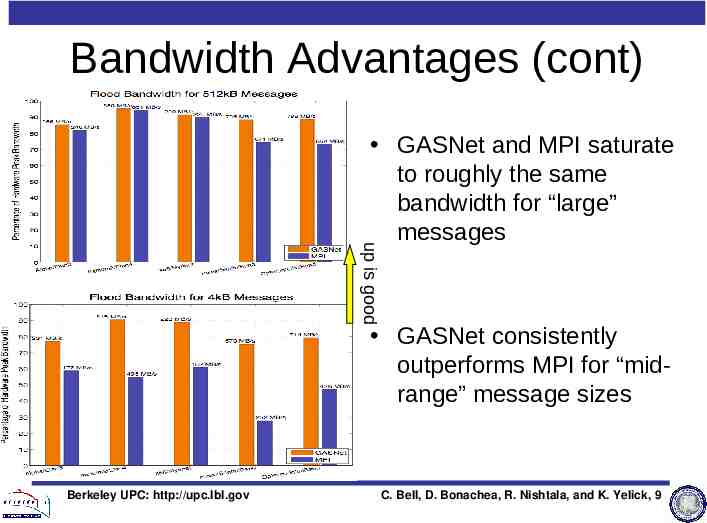
Bandwidth Advantages (cont) up is good GASNet and MPI saturate to roughly the same bandwidth for “large” messages GASNet consistently outperforms MPI for “midrange” message sizes Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 9

A Case Study: NAS FT How to use the potential that the microbenchmarks reveal? Perform a large 3 dimensional Fourier Transform – Used in many areas of computational sciences Molecular dynamics, computational fluid dynamics, image processing, signal processing, nanoscience, astrophysics, etc. Representative of a class of communication intensive algorithms – Sorting algorithms rely on a similar intensive communication pattern – Requires every processor to communicate with every other processor – Limited by bandwidth Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 10

Performing a 3D FFT NX x NY x NZ elements spread across P processors Will Use 1-Dimensional Layout in Z dimension – Each processor gets NZ / P “planes” of NX x NY elements per plane Example: P 4 NZ NZ/P 1D Partition NX NY Berkeley UPC: http://upc.lbl.gov p3 p2 p1 p0 C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 11

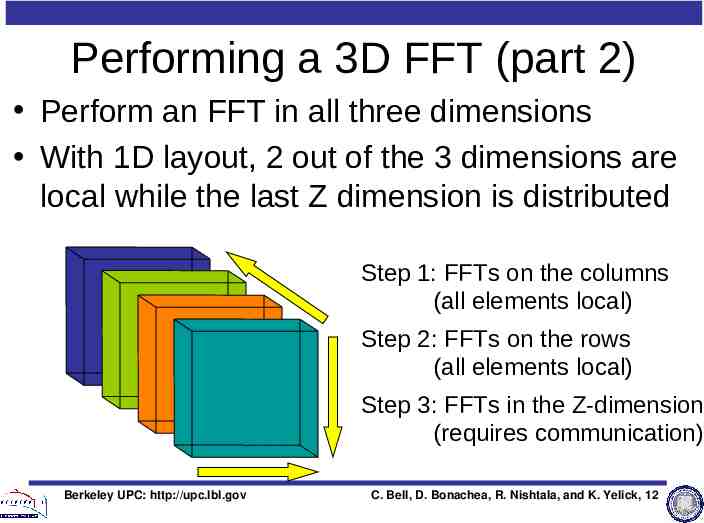
Performing a 3D FFT (part 2) Perform an FFT in all three dimensions With 1D layout, 2 out of the 3 dimensions are local while the last Z dimension is distributed Step 1: FFTs on the columns (all elements local) Step 2: FFTs on the rows (all elements local) Step 3: FFTs in the Z-dimension (requires communication) Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 12

Performing the 3D FFT (part 3) Can perform Steps 1 and 2 since all the data is available without communication Perform a Global Transpose of the cube – Allows step 3 to continue Transpose Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 13

The Transpose Each processor has to scatter input domain to other processors – – Every processor divides its portion of the domain into P pieces Send each of the P pieces to a different processor Three different ways to break it up the messages 1. Packed Slabs (i.e. single packed “Alltoall” in MPI parlance) 2. Slabs 3. Pencils An order of magnitude increase in the number of messages An order of magnitude decrease in the size of each message “Slabs” and “Pencils” allow overlapping communication and computation and leverage RDMA support in modern networks Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 14

Algorithm 1: Packed Slabs Example with P 4, NX NY NZ 16 put to proc 0 1. Perform all row and column FFTs 2. Perform local transpose put to proc 1 – data destined to a remote processor are grouped together put to proc 2 3. Perform P puts of the data put to proc 3 Local transpose Berkeley UPC: http://upc.lbl.gov For 5123 grid across 64 processors – Send 64 messages of 512kB each C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 15

Bandwidth Utilization NAS FT (Class D) with 256 processors on Opteron/InfiniBand – Each processor sends 256 messages of 512kBytes – Global Transpose (i.e. all to all exchange) only achieves 67% of peak point-to-point bidirectional bandwidth – Many factors could cause this slowdown Network contention Number of processors that each processor communicates with Can we do better? Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 16

Algorithm 2: Slabs Waiting to send all data in one phase bunches up communication events Algorithm Sketch plane 0 put to proc 0 – for each of the NZ/P planes Perform all column FFTs for each of the P “slabs” (a slab is NX/P rows) put to proc 1 put to proc 2 – Perform FFTs on the rows in the slab – Initiate 1-sided put of the slab – Wait for all puts to finish – Barrier Non-blocking RDMA puts allow data movement to be overlapped with computation. Puts are spaced apart by the amount of time to perform FFTs on NX/P rows Berkeley UPC: http://upc.lbl.gov put to proc 3 Start computation for next plane For 5123 grid across 64 processors – Send 512 messages of 64kB each C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 17

Algorithm 3: Pencils Further reduce the granularity of communication – Send a row (pencil) as soon as it is ready Algorithm Sketch – For each of the NZ/P planes plane 0 0 0 0 0 1 1 1 1 2 2 2 2 3 3 3 3 Perform all 16 column FFTs For r 0; r NX/P; r – For each slab s in the plane » Perform FFT on row r of slab s » Initiate 1-sided put of row r – Wait for all puts to finish – Barrier Start computation for next plane Large increase in message count Communication events finely diffused through computation – Maximum amount of overlap – Communication starts early Berkeley UPC: http://upc.lbl.gov For 5123 grid across 64 processors – Send 4096 messages of 8kB each C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 18

Communication Requirements 5123 across 64 processors With Slabs GASNet is slightly faster than MPI – Alg 1: Packed Slabs Send 64 messages of 512kB – Alg 2: Slabs Send 512 messages of 64kB – Alg 3: Pencils Send 4096 messages of 8kB GASNet achieves close to peak bandwidth with Pencils but MPI is about 50% less With the message sizes in Packed Slabs both efficient at 8k comm systems reach the same peak bandwidth Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 19

Platforms Name Processor Network Software Opteron/Infiniband “Jacquard” @ NERSC Dual 2.2 GHz Opteron (320 nodes @ 4GB/node) Mellanox Cougar InfiniBand 4x HCA Linux 2.6.5, Mellanox VAPI, MVAPICH 0.9.5, Pathscale CC/F77 2.0 Alpha/Elan3 “Lemieux” @ PSC Quad 1 GHz Alpha 21264 (750 nodes @ 4GB/node) Quadrics QsNet1 Elan3 /w dual rail (one rail used) Tru64 v5.1, Elan3 libelan 1.4.20, Compaq C V6.5-303, HP Fortra Compiler X5.5A-408548E1K Itanium2/Elan4 “Thunder” @ LLNL Quad 1.4 Ghz Itanium2 (1024 nodes @ 8GB/node) Quadrics QsNet2 Elan4 Linux 2.4.21-chaos, Elan4 libelan 1.8.14, Intel ifort 8.1.025, icc 8. 1.029 P4/Myrinet “FSN” @ UC Berkeley Millennium Cluster Dual 3.0 Ghz Pentium 4 Xeon (64 nodes @ 3GB/node) Myricom Myrinet 2000 M3S-PCI64B Linux 2.6.13, GM 2.0.19, Intel ifort 8.120050207Z, icc 8.120050207Z Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 20

Comparison of Algorithms Compare 3 algorithms against original NAS FT – All versions including Fortran use FFTW for local 1D FFTs – Largest class that fit in the memory (usually class D) All UPC flavors outperform original Fortran/MPI implantation by at least 20% – One-sided semantics allow even exchange based implementations to improve over MPI implementations – Overlap algorithms spread the messages out, easing the bottlenecks – 1.9x speedup in the best case Berkeley UPC: http://upc.lbl.gov 2.25 UPC Packed Slabs UPC Slabs UPC Pencils 2 1.75 up is good 2.5 Speedup over NAS Fortran/MPI 1.5 1.25 1 0.75 4 /6 t e in yr 6 2 6 56 12 25 51 25 / / /2 /5 / 3 3 4 4 d n n n an an la la Ba El El E E i / / M / / / 2 2 ha ha fin P4 lp lp In um um / i i A A on an an It It er t p O C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 21

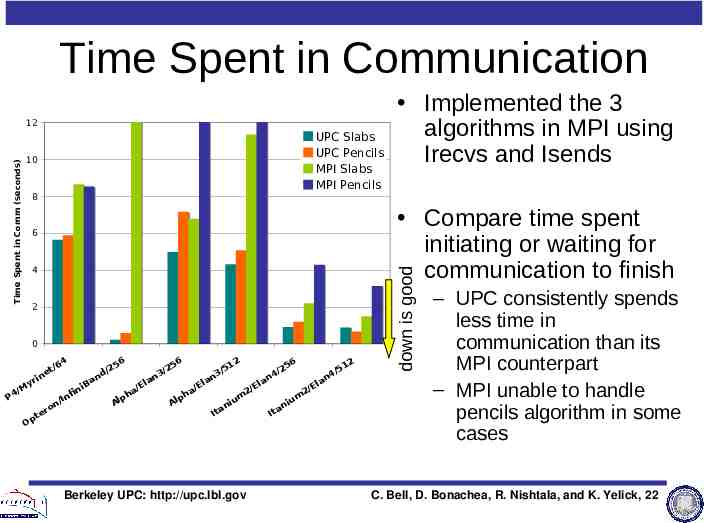
Time Spent in Communication 312.8 UPC Slabs UPC Pencils MPI Slabs MPI Pencils 10 8 4 2 Compare time spent initiating or waiting for communication to finish 0 P M 4/ i yr Op t ne t 4 /6 / on er I ni nfi Ba / nd 6 25 Al a ph l /E a Implemented the 3 algorithms in MPI using Irecvs and Isends 56 /2 3 n Al a ph l /E a 12 /5 3 n n Ita iu m Berkeley UPC: http://upc.lbl.gov E 2/ la / n4 6 25 n Ita iu m E 2/ la / n4 2 51 down is good 6 MPI Crash (Pencils) Time Spent in Comm (seconds) 12 28.6 34.1 – UPC consistently spends less time in communication than its MPI counterpart – MPI unable to handle pencils algorithm in some cases C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 22

Performance Summary 1200 800 up is good MFlops / Proc MFLOPS / Proc 1000 Best NAS Fortran/MPI Best MPI (always Slabs) Best UPC (always Pencils) 600 400 200 0 Platform Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 23

Conclusions One-sided semantics used in GAS languages, such as UPC, provide a more natural fit to modern networks – Benchmarks demonstrate these advantages Use these advantages to alleviate communication bottlenecks in bandwidth limited applications – Paradoxically it helps to send more, smaller messages Both two-sided and one-sided implementations can see advantages of overlap – One-sided implementations consistently outperform two-sided counterparts because comm model more natural fit Send early and often to avoid communication bottlenecks Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 24

Try It! Berkeley UPC is open source – Download it from http://upc.lbl.gov – Install it with CDs that we have here Berkeley UPC: http://upc.lbl.gov C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 25

Contact Us Authors – – – – – Christian Bell Dan Bonachea Rajesh Nishtala Katherine A. Yelick Email us: [email protected] Berkeley UPC: http://upc.lbl.gov Associated Paper: IPDPS ‘06 Proceedings Berkeley UPC Website: http://upc.lbl.gov GASNet Website: http://gasnet.cs.berkeley.edu Special thanks to the fellow members of the Berkeley UPC Group Wei Chen Jason Duell Paul Hargrove Parry Husbands Costin Iancu Mike Welcome C. Bell, D. Bonachea, R. Nishtala, and K. Yelick, 26