Multi-dimensional Sequential Pattern Mining Helen Pinto, Jiawei

Multi-dimensional Sequential Pattern Mining Helen Pinto, Jiawei Han, Jian Pei, Ke Wang, Qiming Chen, Umeshwar Dayal 1

Outline Why multidimensional sequential pattern mining? Problem definition Algorithms Experimental results Conclusions 2

Why Sequential Pattern Mining? Sequential pattern mining: Finding time-related frequent patterns (frequent subsequences) Many data and applications are time-related Customer shopping patterns, telephone calling patterns E.g., first buy computer, then CD-ROMS, software, within 3 mos. Natural disasters (e.g., earthquake, hurricane) Disease and treatment Stock market fluctuation Weblog click stream analysis DNA sequence analysis 3

Motivating Example Sequential patterns are useful Marketing, product design & development Problems: lack of focus “free internet access buy package 1 upgrade to package 2” Various groups of customers may have different patterns MD-sequential pattern mining: integrate multidimensional analysis and sequential pattern mining 4

Sequences and Patterns Given a set of sequences, find the complete set of frequent subsequences A sequence database A sequence : (ef) (ab) (df) c b SID 10 20 30 40 Elements items within an a(abc)(a c)d(cf) element are listed alphabetically ab (ad)c(bc)(ae) a(bc)dc is a subsequence of a(abc) (ef)(ab)(df) cb ab (ac)d(cf) eg(af)cbc Given support threshold min sup 2, (ab)c is a sequential pattern 5 sequence

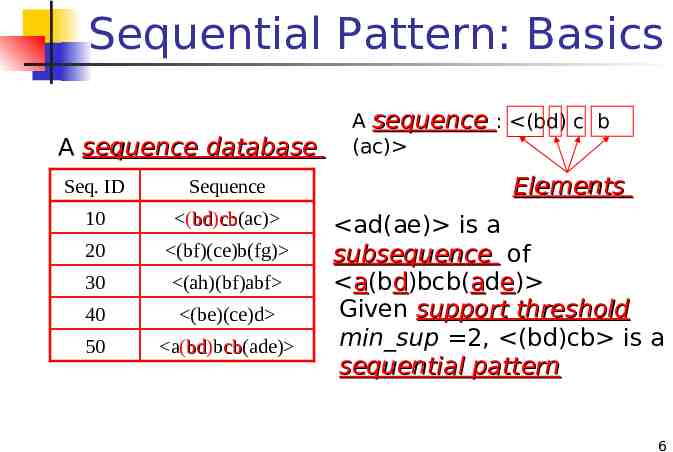
Sequential Pattern: Basics A sequence database Seq. ID Sequence 10 (bd) bd cb(ac) cb 20 (bf)(ce)b(fg) 30 (ah)(bf)abf 40 (be)(ce)d 50 a(bd)b bd cb(ade) cb A sequence : (bd) c b (ac) Elements ad(ae) is a subsequence of a(bd)bcb(ade) Given support threshold min sup 2, (bd)cb is a sequential pattern 6

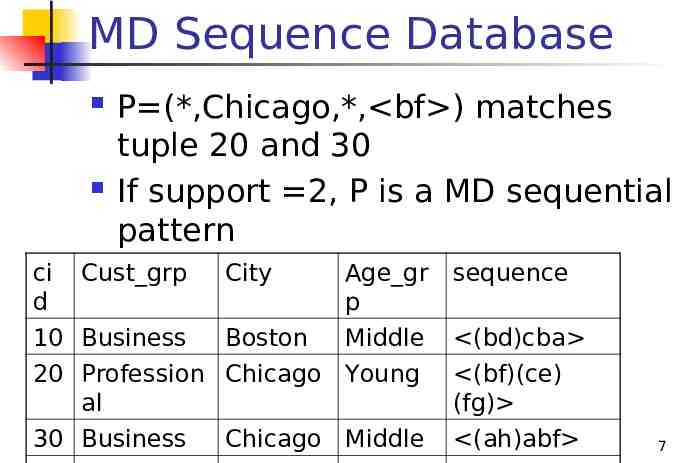
MD Sequence Database ci d P (*,Chicago,*, bf ) matches tuple 20 and 30 If support 2, P is a MD sequential pattern Cust grp 10 Business City Age gr p sequence Boston Middle (bd)cba 20 Profession Chicago Young al (bf)(ce) (fg) 30 Business (ah)abf Chicago Middle 7

Mining of MD Seq. Pat. Embedding MD information into sequences Using a uniform seq. pat. mining method Integration of seq. pat. mining and MD analysis method 8

UNISEQ cid Cust grp Embed MD information into sequences City Age gr sequence Mine the extended p 10 Business Boston Middle (bd)cba 20 Profession al Chicago Young (bf)(ce) (fg) 30 Business Chicago Middle (ah)abf 40 Education New York Retired (be)(ce) ci d sequence database using sequential pattern mining methods MD-extension of sequences 10 (Business,Boston,Middle)(bd)cba 20 (Professional,Chicago,Young)(bf)(ce) (fg) 30 (Business,Chicago,Middle)(ah)abf 9

Mine Sequential Patterns by Prefix Projections Step 1: find length-1 sequential patterns a , b , c , d , e , f Step 2: divide search space. The complete set of seq. pat. can be partitioned into 6 subsets: The ones having prefix a ; The ones having prefix b ; The ones having prefix f SID sequence 10 a(abc) (ac)d(cf) 20 (ad)c(bc)(ae) 30 (ef)(ab)(df)cb 40 eg(af)cbc 10

Find Seq. Patterns with Prefix a Only need to consider projections w.r.t. a a -projected database: (abc)(ac)d(cf) , ( d)c(bc)(ae) , ( b)(df)cb , ( f)cbc Find all the length-2 seq. pat. Having prefix a : aa , ab , (ab) , ac , ad , af Further partition into 6 subsets SID sequence Having prefix aa ; 10 a(abc) (ac)d(cf) 20 (ad)c(bc)(ae) Having prefix af 30 (ef)(ab)(df)cb 40 eg(af)cbc 11

Completeness of PrefixSpan SDB Having prefix a SID sequence 10 a(abc) (ac)d(cf) 20 (ad)c(bc)(ae) 30 (ef)(ab) (df)cb 40 eg(af)cbc Length-1 sequential patterns a , b , c , d , e , f Having prefix c , , f Having prefix b a -projected database b -projected database (abc)(ac)d(cf) Length-2 sequential patterns ( d)c(bc)(ae) aa , ab , (ab) , ( b)(df)cb ac , ad , af ( f)cbc Having prefix aa Having prefix af aa -proj. db af -proj. db 12

Efficiency of PrefixSpan No candidate sequence needs to be generated Projected databases keep shrinking Major cost of PrefixSpan: constructing projected databases Can be improved by bi-level projections 13

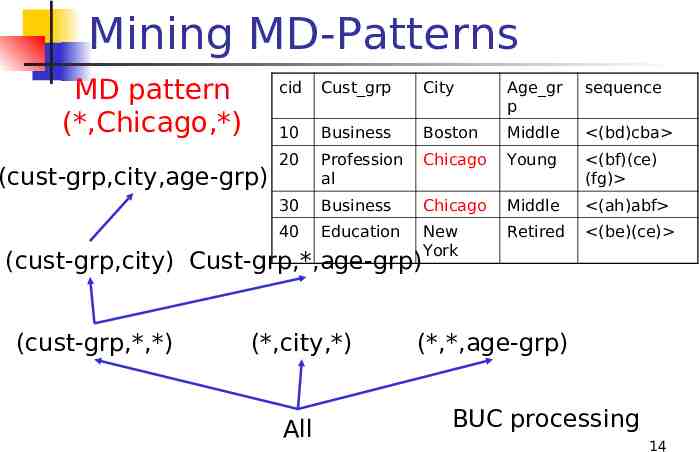
Mining MD-Patterns MD pattern (*,Chicago,*) (cust-grp,city,age-grp) cid Cust grp City Age gr p sequence 10 Business Boston Middle (bd)cba 20 Profession al Chicago Young (bf)(ce) (fg) 30 Business Chicago Middle (ah)abf 40 Education New York Retired (be)(ce) (cust-grp,city) Cust-grp,*,age-grp) (cust-grp,*,*) (*,city,*) All (*,*,age-grp) BUC processing 14

Dim-Seq First find MD-patterns Form projected sequence database E.g. (*,Chicago,*) (bf)(ce)(fg) and (ah)abf for (*,Chicago,*) Find seq. pat in projected database E.g. (*,Chicago,*, bf ) cid Cust grp City Age gr p sequence 10 Business Boston Middle (bd)cba 20 Profession al Chicago Young (bf)(ce) (fg) 30 Business Chicago Middle 15 (ah)abf

Seq-Dim Find sequential patterns Form projected MD-database E.g. bf E.g. (Professional,Chicago,Young) and (Business,Chicago,Middle) for bf Mine MD-patterns E.g. (*,Chicago,*, bf ) cid Cust grp City Age gr p sequence 10 Business Boston Middle (bd)cba 20 Profession al Chicago Young (bf)(ce) (fg) 30 Business Chicago Middle 16 (ah)abf

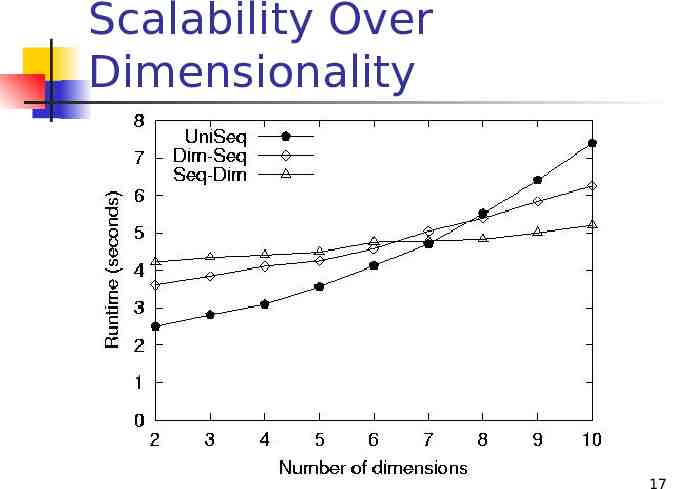
Scalability Over Dimensionality 17

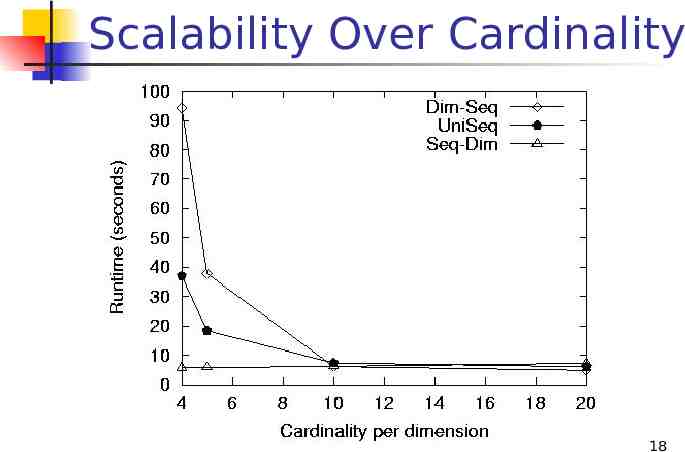
Scalability Over Cardinality 18

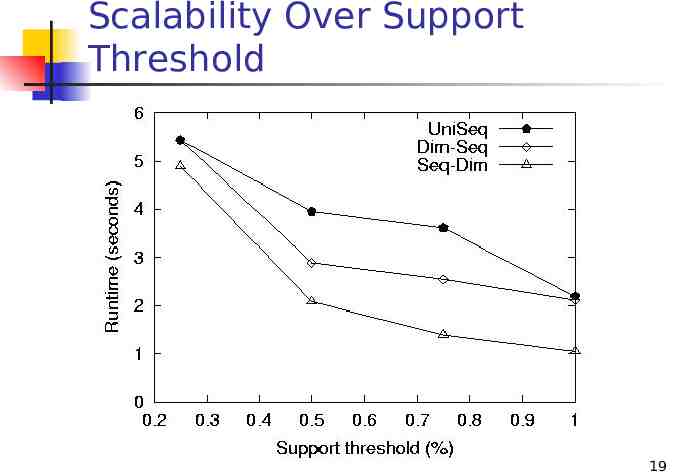
Scalability Over Support Threshold 19

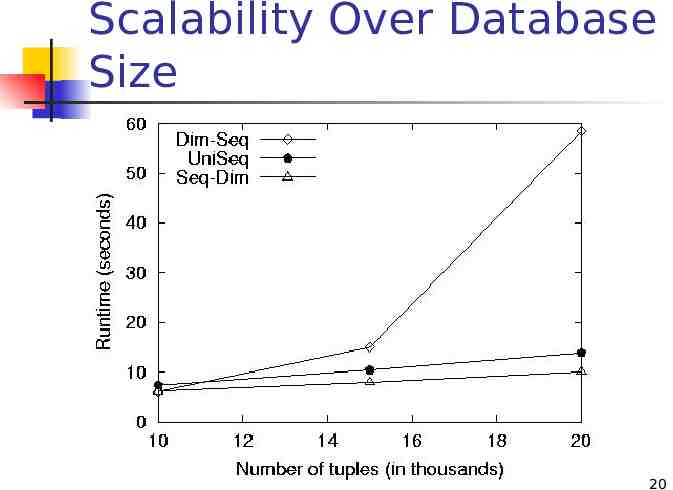
Scalability Over Database Size 20

Pros & Cons of Algorithms Seq-Dim is efficient and scalable UniSeq is also efficient and scalable Fastest in most cases Fastest with low dimensionality Dim-Seq has poor scalability 21

Conclusions MD seq. pat. mining are interesting and useful Mining MD seq. pat. efficiently Uniseq, Dim-Seq, and Seq-Dim Future work Applications of sequential pattern mining 22

References (1) R. Agrawal and R. Srikant. Fast algorithms for mining association rules. VLDB'94, pages 487-499. R. Agrawal and R. Srikant. Mining sequential patterns. ICDE'95, pages 3-14. C. Bettini, X. S. Wang, and S. Jajodia. Mining temporal relationships with multiple granularities in time sequences. Data Engineering Bulletin, 21:32-38, 1998. M. Garofalakis, R. Rastogi, and K. Shim. Spirit: Sequential pattern mining with regular expression constraints. VLDB'99, pages 223234. J. Han, G. Dong, and Y. Yin. Efficient mining of partial periodic patterns in time series database. ICDE'99, pages 106-115. J. Han, J. Pei, B. Mortazavi-Asl, Q. Chen, U. Dayal, and M.-C. Hsu. FreeSpan: Frequent pattern-projected sequential pattern mining. KDD'00, pages 355-359. 23

References (2) J. Han, J. Pei, and Y. Yin. Mining frequent patterns without candidate generation. SIGMOD'00, pages 1-12. H. Lu, J. Han, and L. Feng. Stock movement and n-dimensional intertransaction association rules. DMKD'98, pages 12:1-12:7. H. Mannila, H. Toivonen, and A. I. Verkamo. Discovery of frequent episodes in event sequences. Data Mining and Knowledge Discovery, 1:259-289, 1997. B. "Ozden, S. Ramaswamy, and A. Silberschatz. Cyclic association rules. ICDE'98, pages 412-421. J. Pei, J. Han, B. Mortazavi-Asl, H. Pinto, Q. Chen, U. Dayal, and M.-C. Hsu. PrefixSpan: Mining sequential patterns efficiently by prefixprojected pattern growth. ICDE'01, pages 215-224. R. Srikant and R. Agrawal. Mining sequential patterns: Generalizations and performance improvements. EDBT'96, pages 317. 24