MDP Presentation CS594 Automated Optimal Decision Making Sohail

MDP Presentation CS594 Automated Optimal Decision Making Sohail M Yousof Advanced Artificial Intelligence

Topic Planning and Control in Stochastic Domains With Imperfect Information

Objective Markov Decision Processes (Sequences of decisions) – Introduction to MDPs – Computing optimal policies for MDPs

Markov Decision Process (MDP) Sequential decision problems under uncertainty – Not just the immediate utility, but the longer-term utility as well – Uncertainty in outcomes Roots in operations research Also used in economics, communications engineering, ecology, performance modeling and of course, AI! – Also referred to as stochastic dynamic programs

Markov Decision Process (MDP) Defined as a tuple: S, A, P, R – S: State – A: Action – P: Transition function Table P(s’ s, a), prob of s’ given action “a” in state “s” – R: Reward R(s, a) cost or reward of taking action a in state s Choose a sequence of actions (not just one decision or one action) – Utility based on a sequence of decisions

Example: What SEQUENCE of actions should our agent take? Each action costs –1/25 Agent can take action N, E, S, W Faces uncertainty in every state Reward N 0.8 1 1 2 Blocked CELL 0.1 Reward 0.1 -1 3 Start1 2 3 4

MDP Tuple: S, A, P, R S: State of the agent on the grid (4,3) – Note that cell denoted by (x,y) A: Actions of the agent, i.e., N, E, S, W P: Transition function – Table P(s’ s, a), prob of s’ given action “a” in state “s” – E.g., P( (4,3) (3,3), N) 0.1 – E.g., P((3, 2) (3,3), N) 0.8 – (Robot movement, uncertainty of another agent’s actions, ) R: Reward (more comments on the reward function later) – R( (3, 3), N) -1/25 – R (4,1) 1

?Terminology Before describing policies, lets go through some terminology Terminology useful throughout this set of lectures Policy: Complete mapping from states to actions

MDP Basics and Terminology An agent must make a decision or control a probabilistic system Goal is to choose a sequence of actions for optimality Defined as S, A, P, R MDP models: – Finite horizon: Maximize the expected reward for the next n steps – Infinite horizon: Maximize the expected discounted reward. – Transition model: Maximize average expected reward per transition. – Goal state: maximize expected reward (minimize expected cost) to some target state G.

?Reward Function According to chapter2, directly associated with state – Denoted R(I) – Simplifies computations seen later in algorithms presented Sometimes, reward is assumed associated with state,action – R(S, A) – We could also assume a mix of R(S,A) and R(S) Sometimes, reward associated with state,action,destination-state – R(S,A,J) – R(S,A) R(S,A,J) * P(J S, A) J

Markov Assumption Markov Assumption: Transition probabilities (and rewards) from any given state depend only on the state and not on previous history Where you end up after action depends only on current state – After Russian Mathematician A. A. Markov (1856-1922) – (He did not come up with markov decision processes however) – Transitions in state (1,2) do not depend on prior state (1,1) or (1,2)

?MDP vs POMDPs Accessibility: Agent’s percept in any given state identify the state that it is in, e.g., state (4,3) vs (3,3) – Given observations, uniquely determine the state – Hence, we will not explicitly consider observations, only states Inaccessibility: Agent’s percepts in any given state DO NOT identify the state that it is in, e.g., may be (4,3) or (3,3) – Given observations, not uniquely determine the state – POMDP: Partially observable MDP for inaccessible environments We will focus on MDPs in this presentation.

MDP vs POMDP MDP World World Actions Observations States Agent Agent Actions SE b P

Stationary and Deterministic Policies Policy denoted by symbol

Policy Policy is like a plan, but not quite – Certainly, generated ahead of time, like a plan Unlike traditional plans, it is not a sequence of actions that an agent must execute – If there are failures in execution, agent can continue to execute a policy Prescribes an action for all the states Maximizes state expected reward, rather than just reaching a goal

MDP problem The MDP problem consists of: – Finding the optimal control policy for all possible states; – Finding the sequence of optimal control functions for a specific initial state – Finding the best control action(decision) for a specific state.

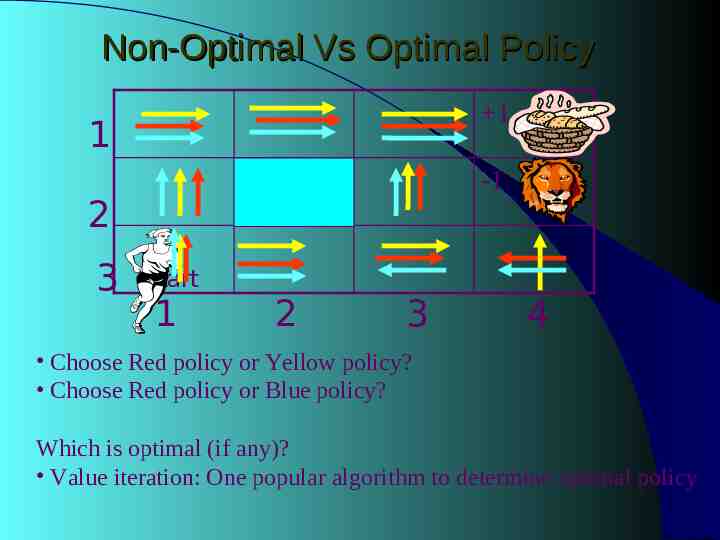
Non-Optimal Vs Optimal Policy 1 1 -1 2 3 Start 1 2 3 4 Choose Red policy or Yellow policy? Choose Red policy or Blue policy? Which is optimal (if any)? Value iteration: One popular algorithm to determine optimal policy

Value Iteration: Key Idea Iterate: update utility of state “I” using old utility of neighbor states “J”; given actions “A” –U t 1 (I) max [R(I,A) P(J I,A)* U t (J)] A J – P(J I,A): Probability of J if A is taken in state I – max F(A) returns highest F(A) – Immediate reward & longer term reward taken into account

Value Iteration: Algorithm Initialize: U0 (I) 0 Iterate: U t 1 (I) max [ R(I,A) P(J I,A)* U t (J) ] A J – Until close-enough (U t 1, Ut) At the end of iteration, calculate optimal policy: Policy(I) argmax [R(I,A) P(J I,A)* U t 1 (J) ] A J

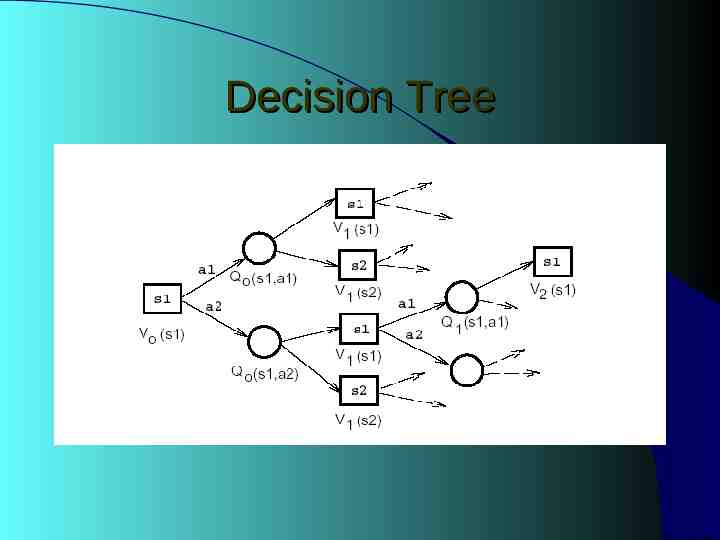
Forward Method for Solving MDP Decision Tree

?Markov Chain Given fixed policy, you get a markov chain from the MDP – Markov chain: Next state is dependent only on previous state – Next state: Not dependent on action (there is only one action) – Next state: History dependency only via the previous state – P(S t 1 St, S t-1, S t-2 .) P(S t 1 St) How to evaluate the markov chain? Could we try simulations? Are there other sophisticated methods around?

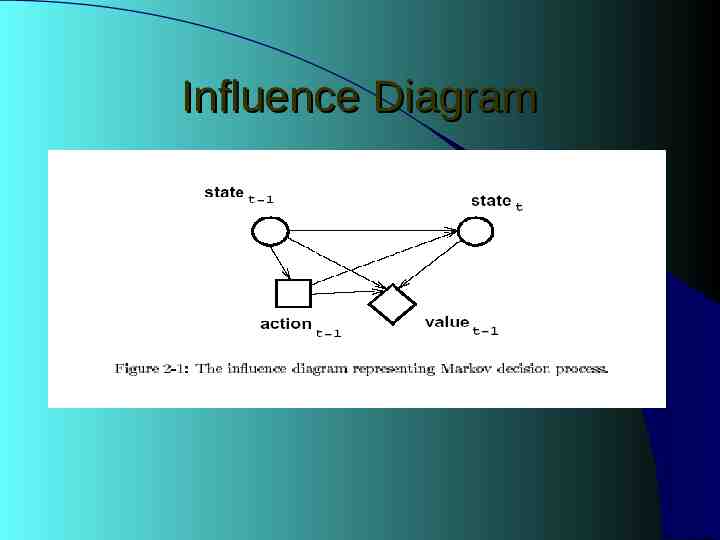
Influence Diagram

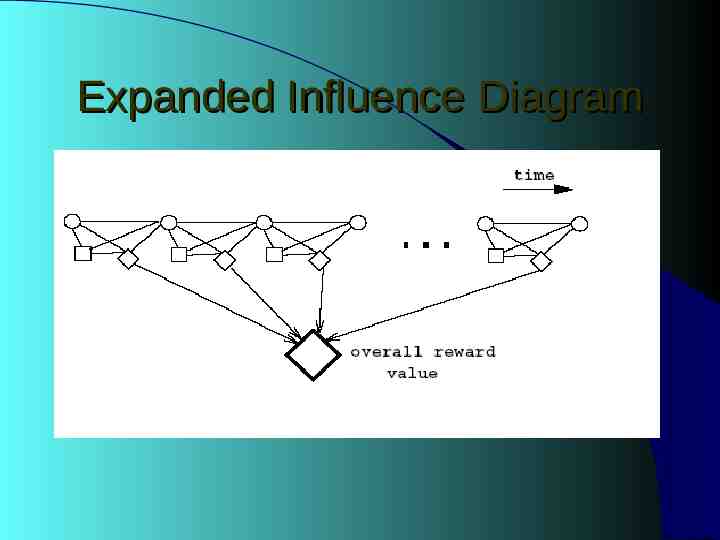
Expanded Influence Diagram

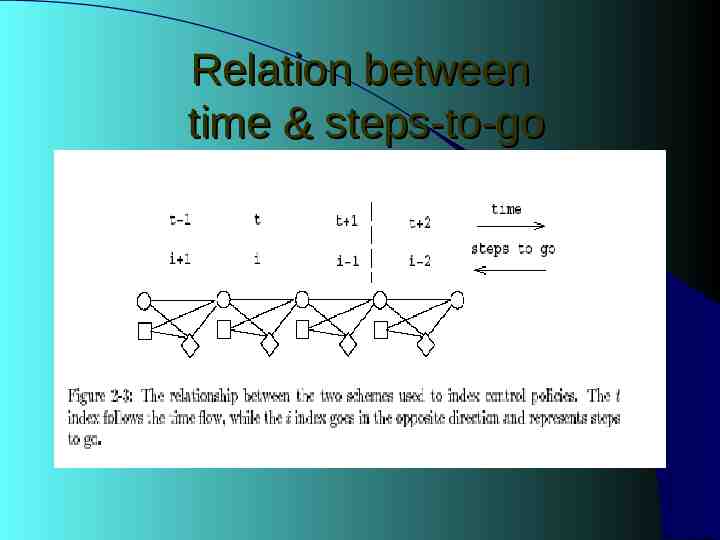
Relation between time & steps-to-go

Decision Tree

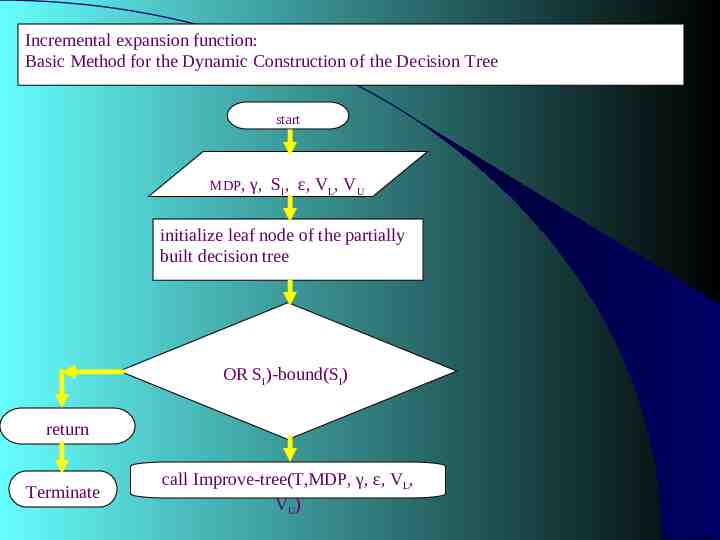
Dynamic Construction of the Decision Tree Incrémental expansion(MDP,γ, sI, є, VL, VU) Initialize tree T with sI and ubound (sI), lbound (sI) using VL, VU; repeat until(single action remains for sI or ubound (sI) - lbound (sI) є call Improve-tree(T,MDP,γ, VL, VU) return action with greatest lover bound as a result; Improve-tree (T,MDP,γ, VL, VU) if root(T) is a leaf then expand root(T) set bouds lbound, ubound of new leaves using V L, VU; else for all decision subtrees T’ of T do call Improve-tree (T,MDP,γ, VL, VU) recompute bounds lbound(root(T)), ubound(root(T))for root(T); when root(T) is a decision node prune suboptimal action branches from T; return;

Incremental expansion function: Basic Method for the Dynamic Construction of the Decision Tree start MDP, γ, SI, ε, VL, VU initialize leaf node of the partially built decision tree OR SI)-bound(SI) return Terminate call Improve-tree(T,MDP, γ, ε, VL, VU)

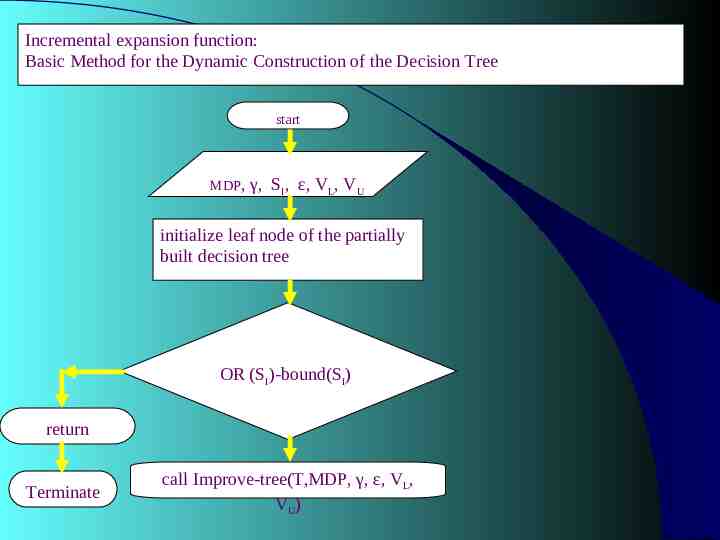
Computer Decisions using Bound Iteration Incrémental expansion(MDP,γ, sI, є, VL, VU) Initialize tree T with sI and ubound (sI), lbound (sI) using VL, VU; repeat until(single action remains for sI or ubound (sI) - lbound (sI) є call Improve-tree(T,MDP,γ, VL, VU) return action with greatest lover bound as a result; Improve-tree (T,MDP,γ, VL, VU) if root(T) is a leaf then expand root(T) set bouds lbound, ubound of new leaves using VL, VU; else for all decision subtrees T’ of T do call Improve-tree (T,MDP,γ, VL, VU) recompute bounds lbound(root(T)), ubound(root(T))for root(T); when root(T) is a decision node prune suboptimal action branches from T; return;

Incremental expansion function: Basic Method for the Dynamic Construction of the Decision Tree start MDP, γ, SI, ε, VL, VU initialize leaf node of the partially built decision tree OR (SI)-bound(SI) return Terminate call Improve-tree(T,MDP, γ, ε, VL, VU)

Solving Large MDP problmes

If You Want to Read More on MDPs If You Want to Read More on MDPs Book: – Martin L. Puterman Markov Decision Processes Wiley Series in Probability – Available on Amazon.com