Learning Curves Dr. Everette S. Gardner, Jr.
15 Slides91.00 KB
Learning Curves Dr. Everette S. Gardner, Jr.
Learning curve concepts Predicts reduction in manufacturing costs or direct labor hours as cumulative production increases Based on empirical evidence rather than theory Learning Curves 2
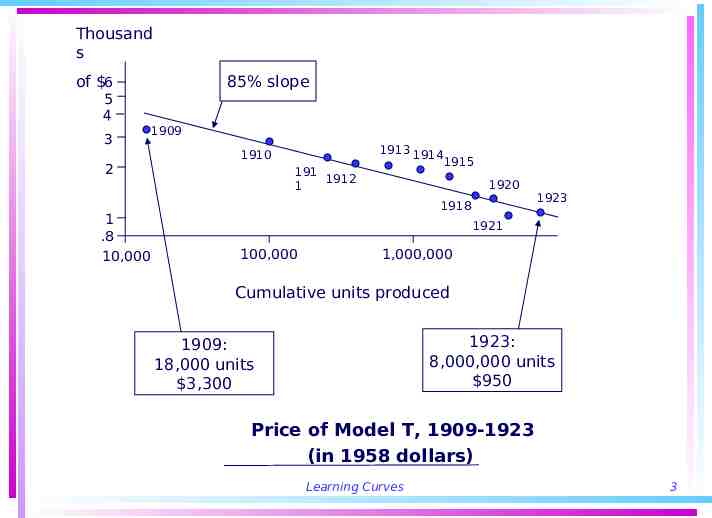
Thousand s of 6 85% slope 5 4 3 2 1 .8 10,000 1909 1913 1914 1910 191 1912 1 1915 1920 1918 1923 1921 100,000 1,000,000 Cumulative units produced 1923: 8,000,000 units 950 1909: 18,000 units 3,300 Price of Model T, 1909-1923 (in 1958 dollars) Learning Curves 3
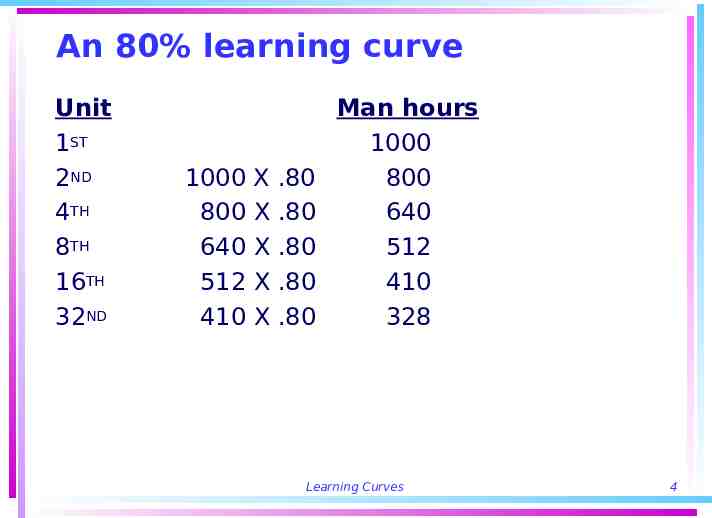
An 80% learning curve Unit 1ST 2ND 4TH 8TH 16TH 32ND 1000 800 640 512 410 X X X X X .80 .80 .80 .80 .80 Man hours 1000 800 640 512 410 328 Learning Curves 4
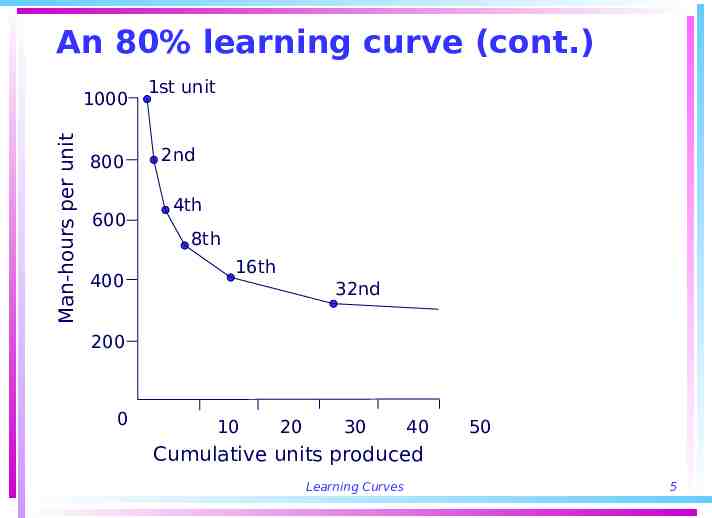
An 80% learning curve (cont.) Man-hours per unit 1000 800 600 400 1st unit 2nd 4th 8th 16th 32nd 200 0 10 20 30 40 50 Cumulative units produced Learning Curves 5
The log - linear method Exponential form: yx kxn Where x unit number yx man-hrs. to produce xth unit k hrs. to produce first unit n log b / log 2 b learning rate (80%, etc.) expressed as decimal (.8, etc.) Logarithmic equation: log yx log k – n (log x) Learning Curves Learn.xls 6
The log - linear method (cont.) yx log yx Cum. units (x) Cum. units (log x) Learning Curves 7
Example calculations yx kxn, n log b / log 2 For 80% LC, b .80 n log .80 / log 2 -.3219 Assume k 1000 y1 1000 (1)-.3219 1000 (1) 1000 y2 1000 (2)-.3219 1000 (.80) 800 y3 1000 (3)-.3219 1000 (.7021) 702 y4 1000 (4)-.3219 1000 (.6400) 640 y100 1000 (100)-.3219 1000 (.2270) 227 Learning Curves 8
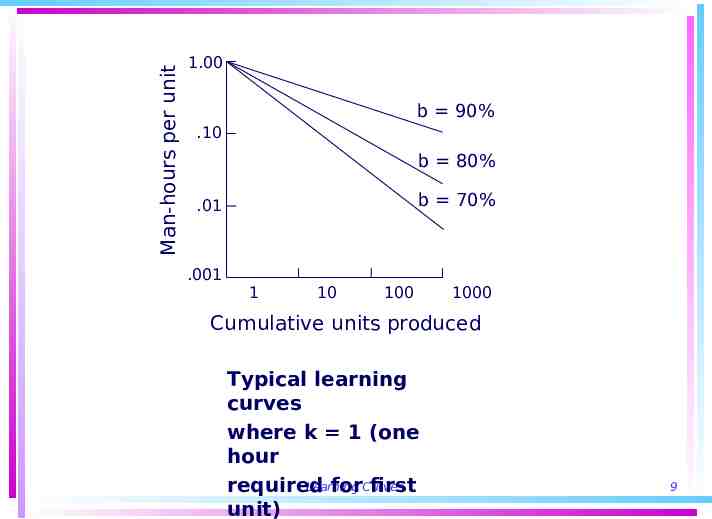
Man-hours per unit 1.00 b 90% .10 b 80% b 70% .01 .001 1 10 100 1000 Cumulative units produced Typical learning curves where k 1 (one hour Learning required forCurves first unit) 9
Forces behind the learning curve 1. Increased labor efficiency 2. Process innovations and methods improvements 3. Substitution effects 4. Product redesign 5. Standardization 6. Economies of scale 7. Shared experience Learning Curves 10
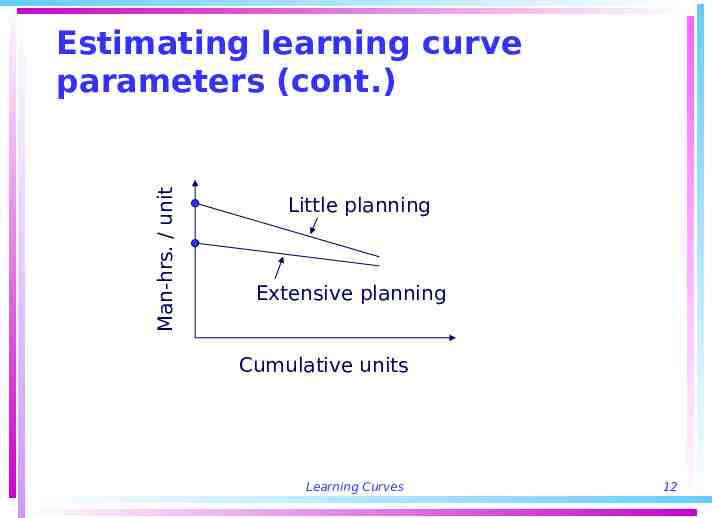
Estimating learning curve parameters The concept applies to an aggregation rather than to individual operations First unit hours rarely known in time to develop curve – must estimate far in advance Slope can be estimated by least-squares regression Comparisons should always be made to similar products/processes – industry data usually available Extensive pre-production planning should result in lower, flatter curve Learning Curves 11
Man-hrs. / unit Estimating learning curve parameters (cont.) Little planning Extensive planning Cumulative units Learning Curves 12
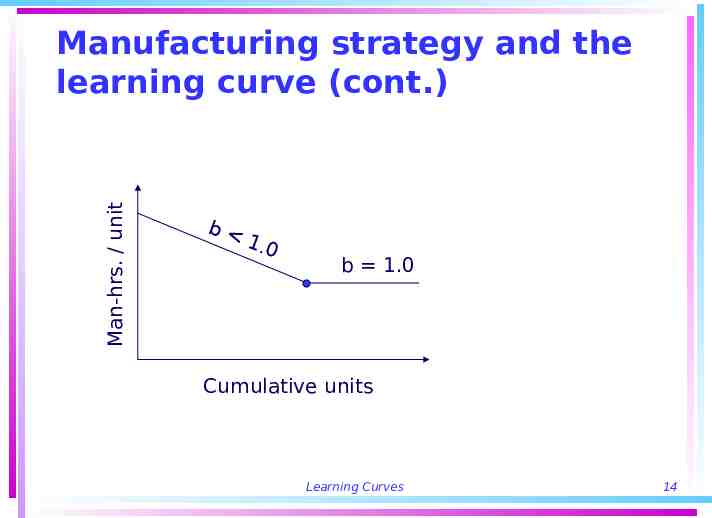
Manufacturing strategy and the learning curve Capacity expands automatically Break-even points reduced automatically Worker compensation plans should account for learning effects The learning curve is a strategic, not a tactical concept – cannot be used as a short-range operating control A learning curve strategy can reduce the ability to innovate At some point, the learning curve will “plateau” Learning Curves 13
Man-hrs. / unit Manufacturing strategy and the learning curve (cont.) b 1.0 b 1.0 Cumulative units Learning Curves 14
Learning curve applications Production planning / EOQ planning Price forecasting Petrochemicals Consumer durable goods Competitive bidding Income reporting in accounting Planning warranty maintenance Washers / dryers Televisions Forecasting industrial accidents Petroleum industry Mining Forecasting automobile accidents on new roadways Learning Curves 15