Key Concept  Which one is harder?  Factoring: Given a number

Key Concept Which one is harder? Factoring: Given a number N, express it as a product of its prime numbers Primality: Given a number N, determine whether it is prime This gulf will be a key to modern encryption algorithms (RSA, etc), which makes secure communication (internet, etc.) currently possible CS 312 - Modular Division and RSA 1

RSA Public Key Encryption To do RSA we need fast Modular Exponentiation which we have shown We also need Modular Division To do Modular Division we use the extended Euclid Algorithm which we will now build towards CS 312 - Modular Division and RSA 2

Euclid’s Rule for GCD How do you find the greatest common divisor of two integers – Largest integer that divides both – Could factor but that is exponential Back in ancient Greece Euclid discovered the rule: If x and y are positive integers with x y then gcd(x,y) gcd(x mod y, y) which gives us the following algorithm Function Euclid (a,b) Input: Two integers a and b with a b 0 (n-bit integers) Output: gcd(a,b) if b 0: return a else: return Euclid(b, a mod b) Why do we care: We will need to know when two integers a and b are relatively prime which is when gcd(a,b) 1 CS 312 - Modular Division and RSA 3

Euclid’s Algorithm Function Euclid (a,b) Input: Two integers a and b with a b 0 (n-bit integers) Output: gcd(a,b) if b 0: return a else: return Euclid(b, a mod b) E(15, 12) E(12, 3) E(3, 0) 3 – E(15, 11) E(11, 4) E(4, 3) E(3, 1) E(1, 0) 1 – 3 is GCD and thus the two integers are not relatively prime 1 is GCD and thus the two integers are relatively prime As soon as b becomes 0, a is the GCD Note: Two integers a and b are relatively prime if gcd(a,b) 1 CS 312 - Modular Division and RSA 4

Euclid’s Algorithm Function Euclid (a,b) Input: Two integers a and b with a b 0 (n-bit integers) Output: gcd(a,b) if b 0: return a else: return Euclid(b, a mod b) Complexity? – Each call reduces the arguments by at least 1/2 CS 312 - Modular Division and RSA 5

Euclid’s Algorithm Function Euclid (a,b) Input: Two integers a and b with a b 0 (n-bit integers) Output: gcd(a,b) if b 0: return a else: return Euclid(b, a mod b) Complexity? – Each call reduces the arguments by at least 1/2 – Thus O(n log2(a)) calls each with one n2 division – Complexity is O(n3) CS 312 - Modular Division and RSA 6

Extended Euclid’s Algorithm function extended-Euclid (a, b) Input: Two positive integers a and b with a b 0 Output: Integers x, y, d such that d gcd(a, b) and ax by d if b 0: return (1, 0, a) (x', y', d) extended-Euclid(b, a mod b) return (y', x' – floor(a/b)y', d) Exact same as Euclid except during stack unraveling This gives us the results we need for modular division We'll do an example in a minute CS 312 - Modular Division and RSA 7

Modular Division - Multiplicative Inverses Every real number a 0 has an inverse 1/a, (a·1/a 1) Dividing z by a is the same as multiplying z by the inverse 1/a Modular division z/a is done by multiplying z by the inverse of a In modular arithmetic we say that x is the multiplicative inverse of a modulo N if ax 1 (mod N) Multiplicative inverse of 3 mod 5 ? CS 312 - Modular Division and RSA 8

Modular Division - Multiplicative Inverses Every real number a 0 has an inverse 1/a, (a·1/a 1) Dividing z by a is the same as multiplying z by the inverse 1/a Modular division z/a is done by multiplying z by the inverse of a In modular arithmetic we say that x is the multiplicative inverse of a modulo N if ax 1 (mod N) Multiplicative inverse of 3 mod 5 2 – We will call 2, a-1 mod N in this case – If a multiplicative inverse exists, it is unique mod N Unlike regular arithmetic many numbers do not have a multiplicative inverse in modular arithmetic What is the multiplicative inverse of 2 mod 4? We need an algorithm to state if the inverse exists and what it is in order to do modular division CS 312 - Modular Division and RSA 9

Modular Division - Multiplicative Inverses In fact, the only time a has a multiplicative inverse mod N is when a and N are relatively prime Two integers a and b are relatively prime if gcd(a,b) 1 (Euclid’s) – The probability that two random numbers are relatively prime is 60.8% If a and N are relatively prime then we know the multiplicative inverse exists (e.g. does 4 mod 7 have an inverse?) CS 312 - Modular Division and RSA 10

Modular Division - Multiplicative Inverses Euclid only shows existence. Extended-Euclid(a, N) does it all for us! – Returns integers x, y, d such that d gcd(a, N) and ax Ny d – First, see if d 1 as the gcd to confirm that a and N are relatively prime – If so, it also finds the multiplicative inverse of a mod N! How? If a and N are relatively prime, then ax Ny 1 Consider the mod N version: ax Ny 1 mod N Ny 0 (mod N) for all integers y Thus, ax 1 (mod N) x is the multiplicative inverse of a modulo N CS 312 - Modular Division and RSA 11

Modular Division Modular N division can only be done with a divisor relatively prime to N and the division is carried out by multiplying the dividend by the inverse Assume we want to divide 9 mod 11 by 3 mod 11 The inverse of 3 mod 11 is 4 (find with extended-Euclid) Then we do the division by multiplying 9 mod 11 by 4 to get 36 mod 11 3 mod 11, which is the answer Assume we want to divide 50 mod 79 by 20 mod 79 – We can if what? CS 312 - Modular Division and RSA 12

Finding the Inverse What is the multiplicative inverse of 20 Mod 79 – Are they relatively prime? – Euclid or extended-Euclid are the algorithms we use to find out (with the extension not needed). The extension only kicks in after the gcd has been found anyway. – Returns integers x, y, d such that d gcd(a, b) and ax by d – x will be the multiplicative inverse if d 1 – Remember we must start with the largest number first so if you have to switch a and b at the beginning (typical in this case since Mod will be greater), then remember to switch x and y at the end CS 312 - Modular Division and RSA 13

Multiplicative Inverse of 20 Mod 79 function extended-Euclid (a, b) if b 0: return (1, 0, a) (x', y', d) extended-Euclid(b, a mod b) return (y', x' – floor(a/b)y', d) a b 79 20 x' y' d // such that ax by d ret 1 CS 312 - Modular Division and RSA ret 2 ret 3 14

Multiplicative Inverse of 20 Mod 79 function extended-Euclid (a, b) if b 0: return (1, 0, a) (x', y', d) extended-Euclid(b, a mod b) return (y', x' – floor(a/b)y', d) // such that ax by d a b x' y' d ret 1 ret 2 ret 3 79 20 1 -1 1 -1 4 1 20 19 0 1 1 1 -1 1 19 1 1 0 1 0 1 1 1 0 1 0 1 ax Ny 1 20(4) 79(-1) Switch x and y since we initially switched a and b Thus x a-1 mod 79 4 Complexity? CS 312 - Modular Division and RSA 15

Modular Division Now we can divide 50 mod 79 by 20 mod 79 The way to do it is to multiply 50 mod 79 by the inverse of 20 mod 79 – We just used Extended Euclid to find that an inverse exists for 20 mod 79 and that it is 4 Then we do the division by multiplying 50 mod 79 by 4 to get 200 mod 79 42 mod 79, which is the answer CS 312 - Modular Division and RSA 16

** Challenge Question ** Multiplicative Inverse of 12 mod 15? function extended-Euclid (a, b) if b 0: return (1, 0, a) (x', y', d) extended-Euclid(b, a mod b) return (y', x' – floor(a/b)y', d) a b 15 12 x' y' d // such that ax by d ret 1 ret 2 ret 3 Fill in all cells and what is the multiplicative inverse? CS 312 - Modular Division and RSA 17

Multiplicative Inverse of 12 mod 15? function extended-Euclid (a, b) if b 0: return (1, 0, a) (x', y', d) extended-Euclid(b, a mod b) return (y', x' – floor(a/b)y', d) // such that ax by d a b x' y' d ret 1 ret 2 ret 3 15 12 0 1 3 1 -1 3 12 3 1 0 3 0 1 3 3 0 1 0 3 ax Ny 3 12(-1) 15(1) (Switched!) However, there is no multiplicative inverse since the gcd 3 and thus a and N are not relatively prime CS 312 - Modular Division and RSA 18

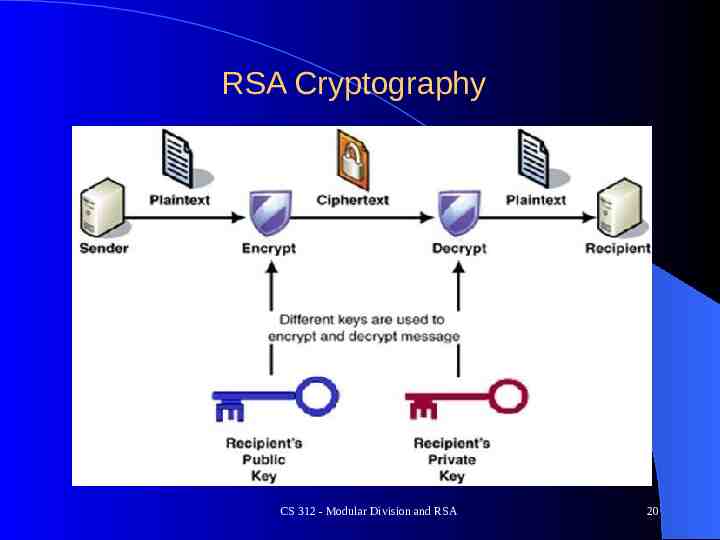
RSA Cryptography Now we have all the algorithms needed to do RSA Public Key Encryption RSA Rivest, Shamir, and Adleman Assume x is the initial message to be sent and e(x) encrypts x into y while d(y) decrypts y back to x Private key approaches - Alice and Bob both know e and d and can thus communicate with each other – but new/unknown people can't Public key - d is the inverse of e. Bob creates e and d and publishes e to everyone, but only he knows d. Alice can create her own pair and publish her own e, etc. Alice e(x) y Bob encrypted y d(y) x Eve CS 312 - Modular Division and RSA 19

RSA Cryptography CS 312 - Modular Division and RSA 20

RSA Encryption Messages are numbers modulo N Messages larger than N are segmented Encryption is a bijection (one-to-one and onto) from {0, 1,., N-1} to {0, 1,., N-1} – a permutation Decryption is its inverse CS 312 - Modular Division and RSA 21

RSA Overview Randomly pick two large primes p and q and let N p · q CS 312 - Modular Division and RSA 22

Generating Random Prime Numbers Generating random primes – An n bit random number has approximately a 1 in n chance of being prime Random Prime Generation Algorithm CS 312 - Modular Division and RSA 23

Generating Random Prime Numbers Generating random primes – An n bit random number has approximately a 1 in n chance of being prime Random Prime Generation Algorithm – Randomly choose an n bit number – Run Primality Test – Probabilistic Fermat Algorithm – If passes, return the number, else choose another number and repeat – O(n) average tries to find a prime, times the Primality test with complexity of O(n3): Total is O(n4) CS 312 - Modular Division and RSA 24

RSA Overview Randomly pick two large primes p and q and let N p · q Choose a number e relatively prime to (p-1)(q-1) – e is often chosen as 3 – permits fast encoding Then the mapping xe mod N is a bijection onto {0, 1,., N1} - Publish (e, N) as the public key for encryption. Keep p and q secret. Find d, the multiplicative inverse of e mod (p-1)(q-1) using extended-Euclid((p-1)(q-1), e) Then for all x {0, 1,., N-1} (xe)d x mod N Keep d private for decryption – Why can't they figure out d? CS 312 - Modular Division and RSA 25

RSA Example Pick two random primes p and q (usually much bigger). p 5 and q 11 Then N p·q 55 Let e 3 – Thus, public key (N, e) (55, 3) Private key: d e-1 mod (p-1)(q-1) 3-1 mod 40 27 – Relatively prime since gcd((p-1)(q-1),e) gcd(40,3) Euclid(40,3) 1 found with extended-Euclid((p-1)(q-1),e) extended-Euclid(40,3) which gives inverse d 27 Encryption of x: y x3 mod 55 – Encryption and decryption use modular exponentiation algorithm Decryption of y: x y27 mod 55 Let x 13 y 133 mod 55 52 mod 55 x 5227 mod 55 13 mod 55 //real keys much longer CS 312 - Modular Division and RSA 26

RSA Summary How could we break RSA - Could try factoring N into primes p and q - no known polynomial algorithm The crux of the security behind RSA – Efficient algorithms / Polynomial time computability for: Modular Exponentiation – modexp() GCD and modular division – extended-Euclid() Primality Testing and creation – fermat() – Absence of sub-exponential algorithms for Factoring The gulf between polynomial and exponential saves the day for cryptography CS 312 - Modular Division and RSA 27