Interest Rate Risk Interest rate changes have significant effects

Interest Rate Risk Interest rate changes have significant effects on many financial firms’ net income, asset value, liability value and equity value (net difference between assets and liabilities). Three Traditional Ways to Measure Interest Rate Risk 1. Repricing Gap - focuses on net interest income changes. 2. Maturity Gap - focuses on equity value changes - ignores cash flow timing. 3. Duration Gap - focuses on equity value including cash flow timing. Duration Gap is the most complete and precise measure.

Repricing Gap The repricing gap is the dollar value of the difference between the book values of assets and liabilities with a certain range of maturity (called a bucket). Steps to Calculate the Repricing Gap and Cumulative Gap 1. List the firm’s assets and liabilities by bucket. 2. Repricing Gap (assets - liabilities) by bucket. 3. Cumulative Gap sum of Repricing Gaps. The effect of interest rate changes on a firm’s net income is NII (Gap) R where NII is the annualized change in net interest income and R is the annual interest rate change.

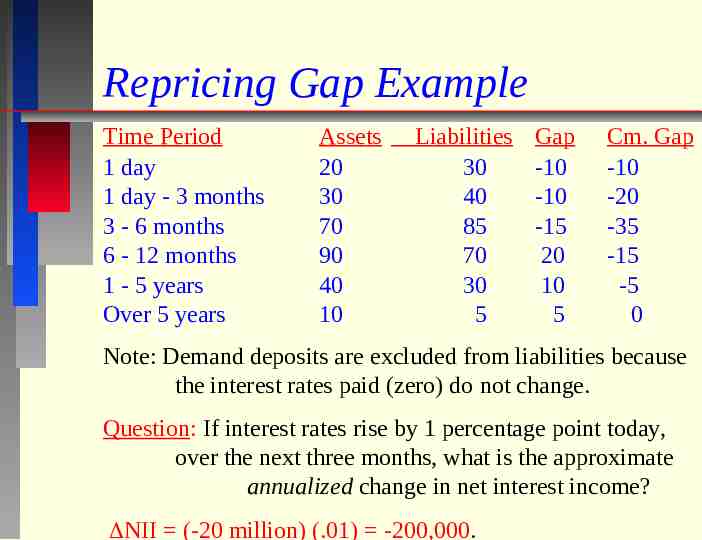
Repricing Gap Example Time Period 1 day 1 day - 3 months 3 - 6 months 6 - 12 months 1 - 5 years Over 5 years Assets 20 30 70 90 40 10 Liabilities 30 40 85 70 30 5 Gap -10 -10 -15 20 10 5 Cm. Gap -10 -20 -35 -15 -5 0 Note: Demand deposits are excluded from liabilities because the interest rates paid (zero) do not change. Question: If interest rates rise by 1 percentage point today, over the next three months, what is the approximate annualized change in net interest income? NII (-20 million) (.01) -200,000.

Weaknesses of Repricing Gap 1. It ignores market value changes of assets and liabilities. 2. Aggregation of assets and liabilities can be misleading when their distributions within a bucket differ. 3. Runoff problems - some assets or liabilities may mature partially or completely before the stated maturity date - e.g., 30 year mortgages seldom last 30 years. 4. Runoffs may be sensitive to interest rate changes. 5. Ignores the effect of off-balance-sheet items. See SLM Holdings 10Q (3/2000) Edgar filing for example.

Example: Chap 8 - Prob. 9 Consider the following balance sheet. Cash 10 Overnight Repos 170 1 mon, 7.05% Tbill 75 7-yr 8.55% Sub. Deb. 150 3 mon, 7.25% Tbill 75 2-yr, 7.5% Tnote 50 8-yr, 8.96% Tnote 100 5-yr, 8.2%, muni 25 (reset - 6 months) Equity 15 Total Assets 335 Total Liab. Equity 335 a. 30 day repricing gap 75 - 170 -95 91 day repricing gap (75 75) - 170 -20 2-yr repricing gap (75 75 50 25) - 170 55

b. 30 day impact of a .5% rise or a .75% drop in all rates. NII (-95 million) (.005) -475,000. NII (-95 million) (-.0075) 712,500 c. Assume one-year runoffs of 10 million for 2-yr Tnote and 20 million for 8-year Tnote. 1-yr repricing gap (75 75 10 20 25) - 170 35 d. Redo part b. NII (35 million) (.005) 175,000. NII (35 million) (-.0075) -262,500

Maturity Gap Model The Maturity Gap measures the difference between a firm’s weighted average asset maturity (MA) and weighted average liability maturity (ML). Maturity Gap (MA - ML) MA WA1MA1 WA2MA2 WA3MA3 WAnMAn ML WL1ML1 WL2ML2 WL3ML3 WLnMLn WAi (market value of asset i)/(market value of total assets). WLi (market value of liability j)/(market value of total liab.) M is the maturity of asset i.

Maturity Gap and the Effect of Interest Rates on Equity Value When (MA - ML) 0 then an increase (decrease) in interest rates is expected to decrease (increase) a financial firm’s equity. When (MA - ML) 0 then an increase (decrease) in interest rates is expected to increase (decrease) a financial firm’s equity. Equity Assets - Liabilities or in change form, Equity Assets - Liabilities Equity, Assets and Liabilities are measured in market value.

Example: Ch 8. 17 - Bond Instead of Mortgage County Bank has the following Balance sheet: Cash 20 Demand Deposits 100 15-yr, 10% Loan 160 5-yr, 6% CD Balloon 210 30-yr, 8% Bond 300 20-yr, 7% Debenture 120 Equity 50 Total Assets 480 Total Liab. And Eq. 480 a. What is the Maturity Gap? MA [0(20) 15(160) 30(300)]/480 23.75 ML [0(100) 5(210) 20(120)]/480 8.02 MGAP 23.75 - 8.02 15.73 years

b. What is the gap if all interest rates rise by 1%? Loan Value 16[PVA 15,.11] 160[PV 15,.11] 148.49 Bond Value 24 [PVA 30,.09] 300[PV 30,.09] 269.08 MA [0(20) 15(148.49) 30(269.08)]/437.6 23.53 CD Value 12.6[PVA 5,.07] 210[PV 5,.07] 201.39 Debenture Value 8.4[PVA 20,.08] 120[PV 20,.08] 108.22 ML [0(100) 5(201.39) 20(108.22)]/409.61 7.99 MGAP 23.53 - 7.99 15.54 c. Market Value of Equity falls by 22 to 28 (437.6 - 409.61).

Duration Gap Model Duration is a better measure of asset or liability interest rate risk than maturity. The duration formula is CFt (t ) t t 1 (1 Y ) D T CFt t t 1 (1 Y ) T time weight x (discount cash flows)/(Bond Price) D CFt Y T duration cash flow in time period t yield to maturity (interest rate) per period maturity in periods - usually semi-annual

A Shorter Way to Calculate a Coupon Bond's Duration (1 Y ) (1 Y ) T (c Y ) D Y c [(1 Y ) T 1] Y where T is the number of payments - for a thirty year bond with semi-annual coupons T 60 c is the coupon rate per period - for a 12% coupon paid semi-annually, c .06. Y is the yield to maturity per period - for a 9% yield with semi-annual coupons Y .045

EXAMPLE: 30 year treasury bond - 12% coupon (paid semi-annually) - 9% yield (1 .045) [(1 .045) 60(.06 .045)] D .045 [.06[(1 .045) 60 1] .045] 20.87 semi-annual periods or 10.44 annual periods Note: Yield and interest rate are used interchangeably here because a bond’s “interest rate” is called its “yield.”

Using Duration to Estimate Bond Price Change Interest rate changes affect the value of promised payments and the value of additional income from reinvested payments. Duration measures both effects. Duration is the elasticity (from economics) of the asset or liability price with respect to a yield change. For a bond paying semi-annual coupons: (Yn Yo ) (1 Y ) % P D x D x (1 Y ) (1 Yo ) Yn Yo D the new semi-annual yield the old semi-annual yield duration in semi-annual periods

EXAMPLE: 30 yr Treasury 12% coupon (paid semiannually) Duration 20.87 semi-annual periods Old yield 9% annual - New Yield 8.5% annual (.0425 .045) % P 20.87 x (1 .045) .05 5% QUESTION: Suppose two bonds are identical except that one pays annual coupons and the other pays semi-annual coupons. Do they have the same duration? If not, which is larger? - Annual

Duration Gap Similar to the Maturity Gap, Duration Gap measures the difference between a firm’s weighted average asset Duration (DA) and weighted average liability Duration (DL). Duration Gap (DA - DL) DA WA1DA1 WA2DA2 WA3DA3 WAnDAn DL WL1DL1 WL2DL2 WL3DL3 WLnDLn WAi (market value of asset i)/(market value of total assets). WLi (market value of liability j)/(market value of total liab.) D is the duration of asset i.

Duration and the Effect of Interest Rates on Equity Value A more precise measure of the effect of an interest rate change on a financial firm’s equity value is: Equity -[DA - kDL]A(Yn - Yo)/(1 Yo) where k L/A and [DA - kDL] is the leverage-adjusted Duration Gap, hereafter referred to as just the Duration Gap. To eliminate the effect of interest rate changes on the value of a firm’s equity (called immunization), some have suggested setting Maturity Gap (MA - ML) 0 Duration Gap (DA - DL) 0. or

A more precise way to “immunize” equity value is by setting [DA - kDL] 0. A typical situation is that the dollar amount of assets (A) and liabilities (L) are given, then we select particular assets and liabilities with durations DA and DL so [DA - kDL] 0. For solvent firms, we know that (A - L) E 0 and k 1 so that equity immunization requires DA DL. Many financial firms have DA DL ,which implies that they are not immunized. To immunize equity as a percent of assets (E/A), setting DA DL is the proper method.

Example: Ch. 9, 20 The balance sheet of Gotbucks Bank is Cash 30 8%, 2-yr Deposits 8.5% Fed. Funds 20 8.5% Fed. Funds 11% Float Loan 105 9% Euro CD 12%, 5-yr Loan 65 Equity Total Assets 220 Total Liabilities a. Fixed Loan Duration D 20 50 130 20 220 (1 .12) [(1 .12) 5(.12 .12)] 4.03 .12 [.12[(1 .12) 1] .12] 5 b. Assuming Floating Rate and Fed Funds have .36 duration Asset Duration [30(0) 65(4.03) 125(.36)]/220 1.4 c. Deposits Duration D (1 .08) [(1 .08) 2(.08 .08)] 1.925 2 .08 [.08[(1 .08) 1] .08]

d. Assuming the Euro CD has .401 duration, Liab. Duration [20(1.925) 180(.401)]/200 .5535 e. Duration Gap 1.4 - (200/220)(.5535) .8938 years. f. An 1% increase in interest rates decreases equity by E -.8938(.01)*220 -1,966,360 g. A decrease of .5% in interest rates increases equity by E -.8938(-.005)*220 983,180 h. To eliminate the effects on equity, the bank can increase liability its duration to 1.54 [x – (200/220)(.5535) 0], decrease its asset duration to .5032 [1.4 – (200/220)(x) 0], or some combination of the two.

Criticisms of Duration and Equity Immunization 1. As interest rates change, durations change, so one must constantly rebalance assets and liabilities to keep immunized. Transactions costs may be large. 2. We have assumed all interest rates change by the same amount but this is seldom true. 3. We have ignored default risk. Default or payment rescheduling can increase or decrease duration. 4. Durations of floating rate instruments and demand deposits are unclear. For floating rate instruments we usually assume duration equals the time to repricing. Demand deposits’ duration is assumed to be zero or small.

5. The most significant criticism is that duration is an approximation and works best for small changes in yields. Convexity (CX) is a measure of the duration error when yield changes are large. To get a better approximation to price changes due to interest rate changes, one can adjust an earlier price change equation to: (1 Y ) (Y Y ) % P D x D x .5CX (Y Y ) (1 Y ) (1 Y ) n o n o The change in equity value becomes: Equity -[DA - kDL]A(Yn - Yo)/(1 Yo) .5[CXA - kCXL]A(Yn - Yo)2 o 2

Example of Using Convexity Husky Financial has 100 million of assets with a weighted average duration of 8.5, a weighted average convexity of 200 and a yield of 10%. It also has 80 million of liabilities with a weighted average duration of 6, a weighted average convexity of 40 and a yield of 10%. If market yields rise by 2 percentage points, what is the expected change in Husky’s equity value if convexity is ignored? How about if one considers convexity? Equity -[8.5 - .8(6)]100(.02)/(1 .10) - 6.7 MM with convexity Equity - 6.7 .5[200 - .8(40)]100(.02)2 - 3.26 M Here, ignoring convexity overestimates the negative change.