Integer Programming Approaches for Automated Planning Menkes van

Integer Programming Approaches for Automated Planning Menkes van den Briel Department of Industrial Engineering Arizona State University [email protected] http://www.public.asu.edu/ dbvan1/ 1

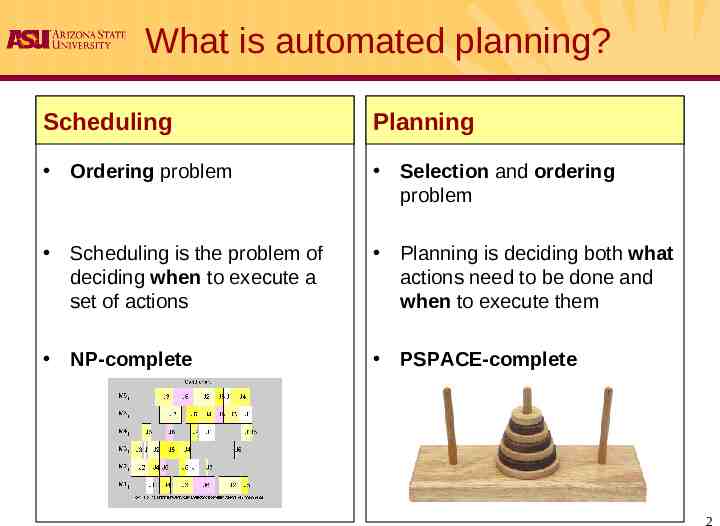
What is automated planning? Scheduling Planning Ordering problem Selection and ordering problem Scheduling is the problem of deciding when to execute a set of actions Planning is deciding both what actions need to be done and when to execute them NP-complete PSPACE-complete 2

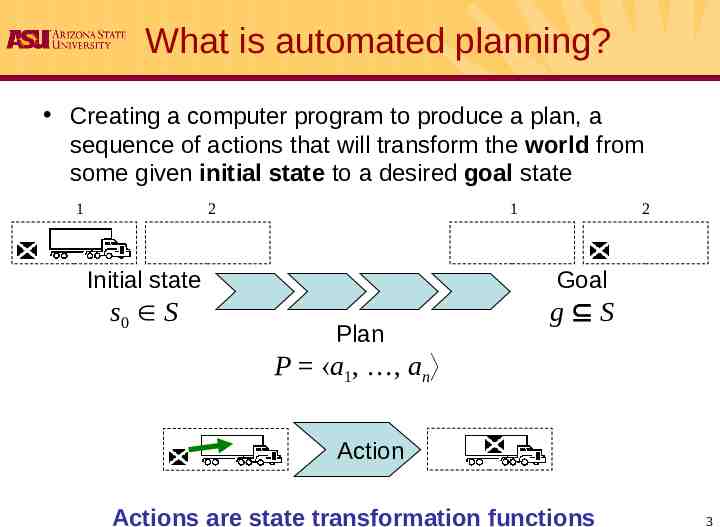
What is automated planning? Creating a computer program to produce a plan, a sequence of actions that will transform the world from some given initial state to a desired goal state 1 1 2 2 Initial state Goal s0 S g S Plan P a1, , an Action Actions are state transformation functions 3

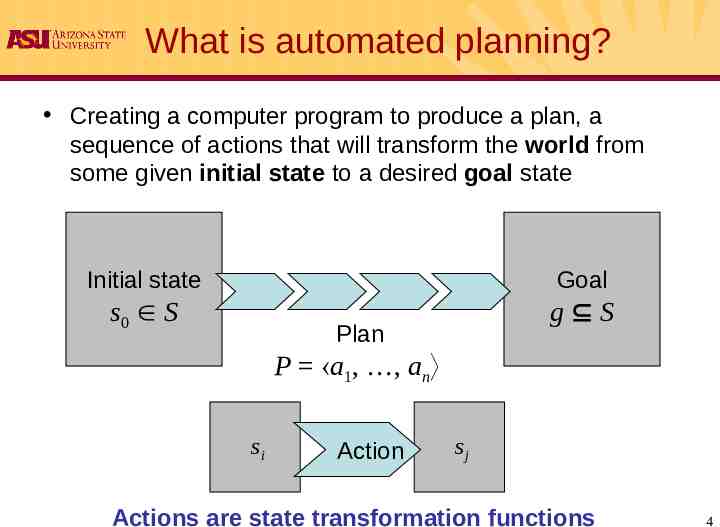
What is automated planning? Creating a computer program to produce a plan, a sequence of actions that will transform the world from some given initial state to a desired goal state Initial state Goal s0 S g S Plan P a1, , an si Action sj Actions are state transformation functions 4

Planning applications Autonomous vehicles – Mars rovers – Underwater robotics – Remote agent experiment Games – Bridge Baron – General game playing Others – Manufacturing process planning – Composition of web services – Cyber Security North Q 9 A A J 7 K 9 6 5 5 3 West 2 East 6 8 Q South 5

Planning by integer programming Scheduling Planning Operations research (OR) Artificial intelligence (AI) Scheduling problems typically involve solving hard optimization problems Planning problems typically involve solving hard feasibility problems Integer programming (IP), branch-and-bound Constraint satisfaction, satisfiability (SAT), A* search 6

Planning by integer programming Very little focus on integer programming approaches for planning – – – – – – [Bylander, 1997] [Bockmayr and Dimopoulos, 1998, 1999] [Kautz and Walser, 1999] [Vossen et al., 1999] [Dimopoulos, 2001] [Dimopoulos and Gerevini, 2002] 7

Why this lack of interest? 1. IP-based approaches simply don’t work – “Lplan [a linear programming-based heuristic for optimal planning] was often slower than the other algorithms primarily due to the time to evaluate the linear programming heuristic” [Bylander, 1997] 2. SAT-based approaches are much faster – SAT-based planners have successfully participated in IPC1, IPC2, IPC4, and IPC5 3. Traditionally there has been little focus on plan quality – Planning is PSPACE-complete, so finding a feasible plan is already hard enough 8

Counter arguments 1. IP-based approaches do work – Optiplan, first IP-based planner to take part in the IPC series – Ranked 2nd in four out of seven domains in IPC4 in the optimal track for propositional domains 2. IP-based approaches can compete with SAT-based approaches – Represent planning as a set of interdependent network flow problems – Generalize the notion of action parallelism 3. Shift in focus towards optimal planning – Applied formulations to partial satisfaction planning problems – Developed a novel framework for optimal planning – Utilized LP relaxations in deriving quality sensitive heuristics 9

Contributions 1. IP-based approaches do work – [Van den Briel, and Kambhampati. Journal of Artificial Intelligence Research, 2005] 2. IP-based approaches can compete with SAT-based approaches – [Van den Briel, Vossen, and Kambhampati. ICAPS, 2005] – [Van den Briel, Vossen, and Kambhampati. Journal of Artificial Intelligence Research, 2008] 3. Shift in focus towards optimal planning – – – – [Van den Briel, et al. AAAI, 2004] [Do, Benton, van den Briel, and Kambhampati. IJCAI, 2007] [J. Benton, van den Briel, and Kambhampati. ICAPS, 2007] [Van den Briel, Benton, Kambhampati, and Vossen. CP, 2007] 10

1. IP approaches do work Optiplan – IP-based planner that extends the state change formulation by [Vossen et al., 1999] [van den Briel, and Kambhampati, 2005] 11

Summary of results International planning competition (IPC) – Bi-annual event – Provides data sets (domains) that are used as benchmarks IPC4 – 7 competition domains – 7 participating planners in the “optimal” track Domains – Pipesworld Control the flow of oil derivatives through a pipeline network, obeying various constraints such as product compatibility and tankage restrictions – Satellite Collect image data with a number of satellites – Philosophers, Optical telegraph Involves finding deadlocks in communication protocols 12

Summary of results 10000 1000 100 10 Satplan04 Optiplan CPT HSPS-A TP4 1 0.1 0.01 1 3 5 7 9 11 13 15 17 19 21 23 25 27 Solution time (sec.) Solution time (sec.) 10000 1000 100 10 Satplan04 Optiplan CPT HSPS-A TP4 1 0.1 0.01 29 1 Phillosophers 3 4 5 6 7 8 9 10 11 12 13 14 Optical telegraph 10000 10000 1000 100 10 Satplan04 1 Optiplan 0.1 CPT 0.01 Solution time (sec.) Solution time (sec.) 2 1000 100 10 1 Satplan04 Optiplan 0.1 CPT 0.01 1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 Pipesworld(tankage) 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 Satellite 13

2. IP versus SAT approaches 1. Represent planning as a set of interdependent network flow problems – One network flow problem for each state variable in the planning domain – Nodes correspond to the values of the state variables, arcs correspond to the value transitions 2. Generalize the notion of action parallelism – Reduces the plan length of the solution plan (and thus the size of the formulation) 14

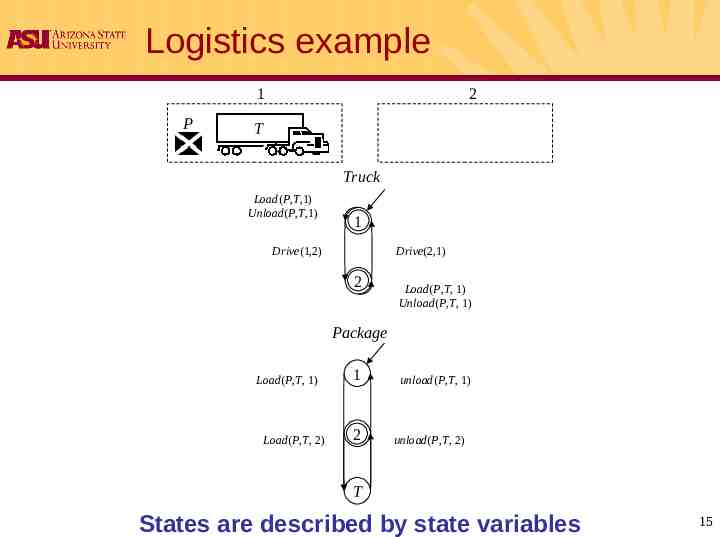
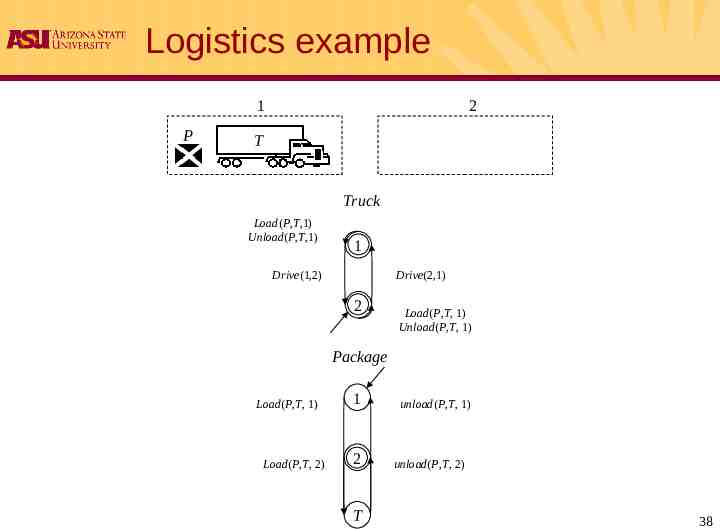
Logistics example 1 P 2 T Truck Load(P,T,1) Unload(P,T,1) 1 Drive(1,2) Drive(2,1) 2 Load(P,T, 1) Unload(P,T, 1) Package Load(P,T, 1) Load(P,T, 2) 1 2 unload(P,T, 1) unload(P,T, 2) T States are described by state variables 15

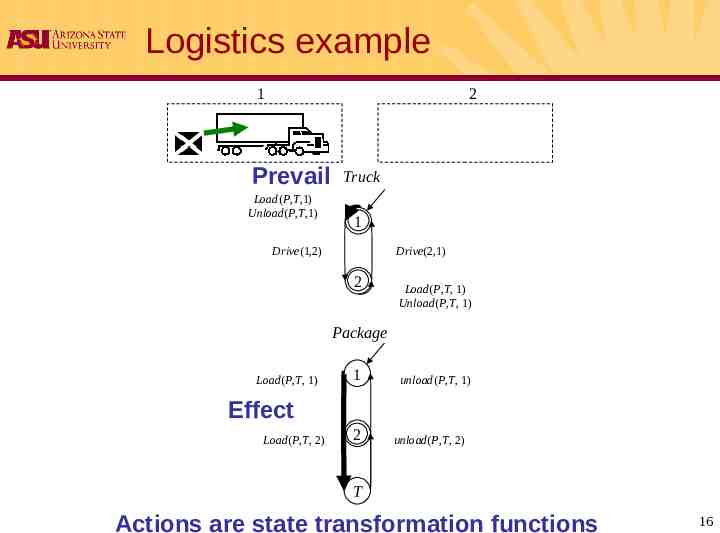
Logistics example 1 2 Prevail Load(P,T,1) Unload(P,T,1) Truck 1 Drive(1,2) Drive(2,1) 2 Load(P,T, 1) Unload(P,T, 1) Package Load(P,T, 1) 1 unload(P,T, 1) Effect Load(P,T, 2) 2 unload(P,T, 2) T Actions are state transformation functions 16

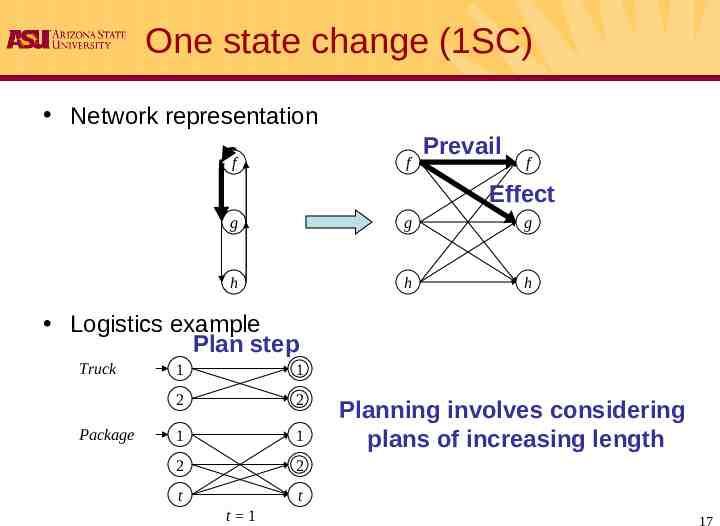
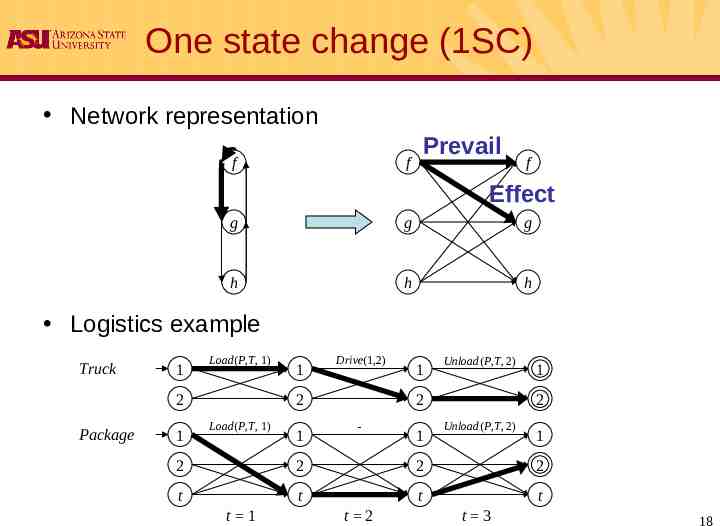
One state change (1SC) Network representation f f Prevail f Effect g g g h h h Logistics example Plan step Truck Package 1 1 2 2 1 1 2 2 t t t 1 Planning involves considering plans of increasing length 17

One state change (1SC) Network representation f Prevail f f Effect g g g h h h Logistics example Truck 1 Load(P,T, 1) 2 Package 1 1 Drive(1,2) 2 Load(P,T, 1) 1 1 Unload(P,T, 2) 2 - 1 1 2 Unload(P,T, 2) 1 2 2 2 2 t t t t t 1 t 2 t 3 18

1SC formulation Constraints – State changes (network flow), for all c C g C ycf,g,t 1{f I} for f Dc h C ycg,h,t 1 f C ycg,h,t for f Dc , 1 t T f C ycf,g,T 1 for g G – Effect implications, for all c C, 1 t T a A:(f,g) SC(a) xa,t ycf,g,t xa,t ycf,f,t for f, g Dc, f g for a A, f PR(a) 19

Summary of results Experimental setup – Domains from IPC2, IPC3 – Comparing 1SC formulation versus SATPLAN04 (winner of the “optimal“ track IPC4) – 2.67GHz CPU with 1.0GB memory Domains – Logistics, Driverlog Involves driving trucks (and flying airplanes) around to deliver packages between locations – Blocksworld Stacking and unstacking towers of blocks – Zenotravel Transporting people around in planes, using different modes of movement: fast and slow 20

Summary of results 1000 1000 SAT4 1SC Solution time (sec.) Solution time (sec.) 10000 100 10 1 0.1 0.01 SAT4 1SC 100 10 1 0.1 0.01 1 2 3 4 5 6 7 8 9 10 1112 1314 1516 1718 1920 1 2 3 4 5 6 7 8 9 10 111213 14 1516 1718 1920212223242526272829303132333435 Blocksmove 1000 1000 SAT4 1SC 100 100 Time (seconds) Solution time (sec.) 10000 10 1 10 1 0.1 0.1 0.01 Driverlog SAT4 1SC 0.01 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 212223 24 2526 2728 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Logistics Zenotravel 21

2. IP versus SAT approaches 1. Represent planning as a set of interdependent network flow problems – One network flow problem for each state variable in the planning domain – Nodes correspond to the values of the state variables, arcs correspond to the value transitions 2. Generalize the notion of action parallelism – Reduces the plan length of the solution plan (and thus the size of the formulation) 22

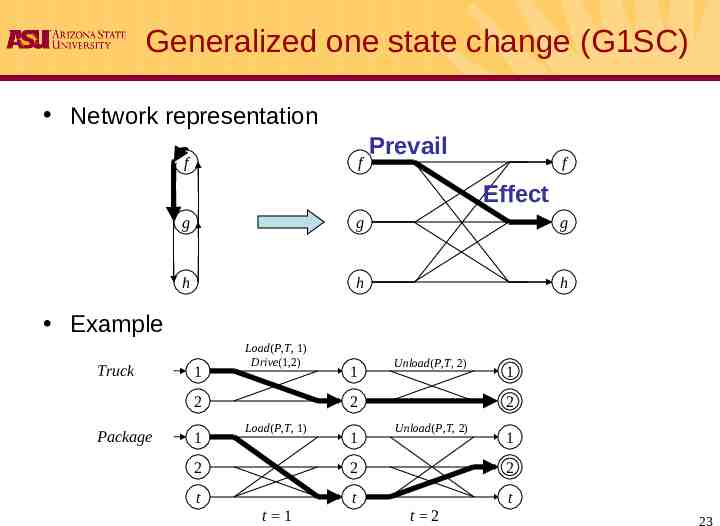
Generalized one state change (G1SC) Network representation f f Prevail f Effect g g g h h h Example Truck 1 Load(P,T, 1) Drive(1,2) 2 Package 1 1 Unload(P,T, 2) 2 Load(P,T, 1) 1 1 2 Unload(P,T, 2) 1 2 2 2 t t t t 1 t 2 23

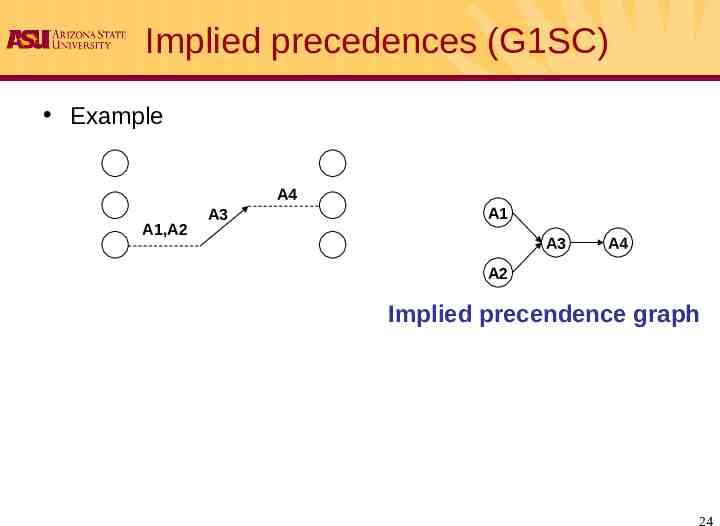
Implied precedences (G1SC) Example A4 A1,A2 A3 A1 A3 A4 A2 Implied precendence graph 24

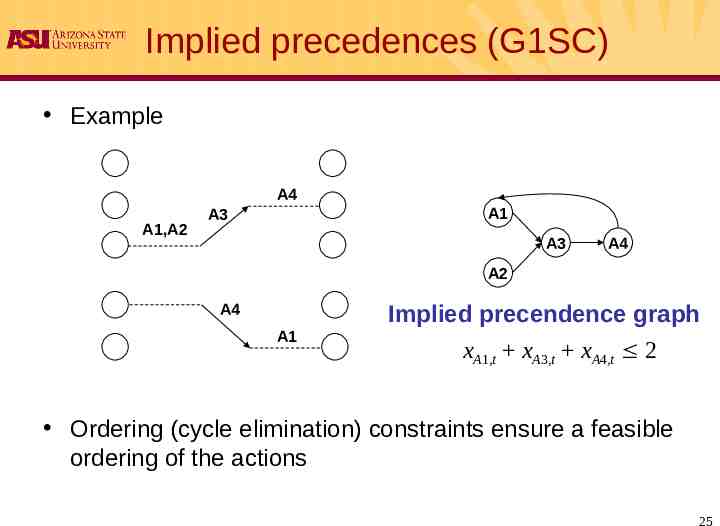
Implied precedences (G1SC) Example A4 A1,A2 A1 A3 A3 A4 A2 A4 A1 Implied precendence graph xA1,t xA3,t xA4,t 2 Ordering (cycle elimination) constraints ensure a feasible ordering of the actions 25

G1SC formulation Constraints – State changes (network flow), for all c C g C ycf,g,t 1{f I} for f Dc h C ycg,h,t 1 f C ycg,h,t for f Dc, 1 t T f C ycf,g,T 1 for g G – Effect implications, for all c C, 1 t T a A:(f,f) SC(a) xa,t ycf,g,t for f, g Dc, f g, xa,t ycf,f,t g Dc:f g (ycg,f,t ycf,g,t) for a A, f PR(a) – Ordering (Cycle elimination) constraints a V( ) xa,t V( ) – 1 for all cycles G, 1 t T 26

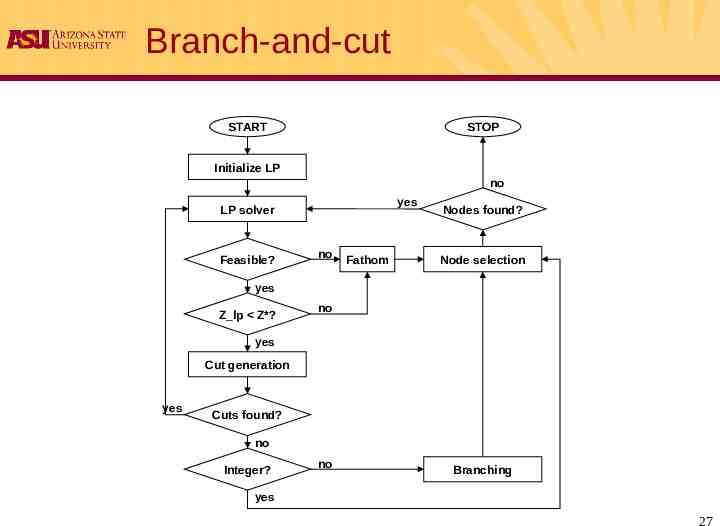
Branch-and-cut START STOP Initialize LP no yes LP solver Feasible? no Fathom Nodes found? Node selection yes Z lp Z*? no yes Cut generation yes Cuts found? no Integer? no Branching yes 27

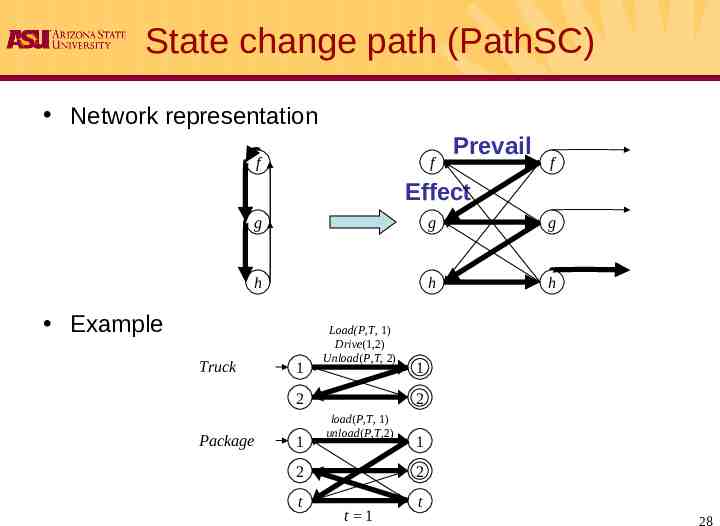
State change path (PathSC) Network representation f f Prevail f Effect g g g h h h Example Truck 1 Load(P,T, 1) Drive(1,2) Unload(P,T, 2) 2 Package 1 1 2 load(P,T, 1) unload(P,T,2) 1 2 2 t t t 1 28

Summary of results 20 16 SAT4 1SC 1SC 12 G1SC Plan length Plan length 15 SAT4 PathSC 10 G1SC PathSC 8 4 5 0 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 17 18 192021222324 2526272829303132333435 Blocksmove 20 Driverlog 12 SAT4 1SC 9 G1SC Plan length Plan length 15 7 8 9 10 11 12 13 14 15 16 17 18 19 20 PathSC 10 6 SAT4 1SC 3 5 G1SC PathSC 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 Logistics 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Zenotravel 29

Summary of results 1000 100 10000 SAT4 Solution time (sec.) Solution time (sec.) 10000 1SC G1SC PathSC 10 1 0.1 0.01 1000 100 100 G1SC PathSC 1 0.1 0.01 1 2 3 4 5 6 7 8 9 101112131415 1617181920 1 2 3 4 5 6 7 8 9 10 111213 14 1516 1718 1920212223242526272829303132333435 Driverlog 1000 SAT4 1SC Time (seconds) Solution time (sec.) 1000 1SC 10 Blocksmove 10000 SAT4 G1SC PathSC 10 1 100 10 SAT4 1 1SC 0.1 g1SC 0.1 0.01 kSC 0.01 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 212223 24 2526 2728 1 2 3 4 5 6 7 8 9 10 1112 1314 1516 1718 1920 Logistics Problems (Zenotravel) [van den Briel, Vossen, and Kambhampati, 2005, 2008] 30

3. Shift towards optimal planning Applied formulations to partial satisfaction planning problems Developed a novel framework for optimal planning Utilized LP relaxations in deriving quality sensitive heuristic search approaches 31

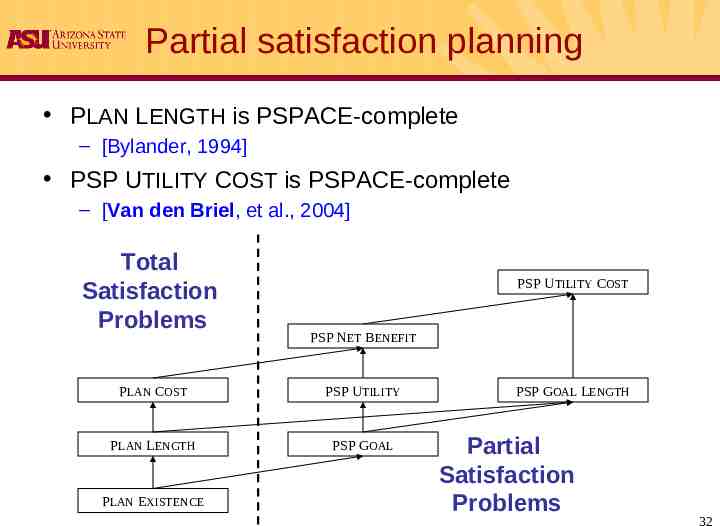
Partial satisfaction planning PLAN LENGTH is PSPACE-complete – [Bylander, 1994] PSP UTILITY COST is PSPACE-complete – [Van den Briel, et al., 2004] Total Satisfaction Problems PSP UTILITY COST PSP NET BENEFIT PLAN COST PSP UTILITY PLAN LENGTH PSP GOAL PLAN EXISTENCE PSP GOAL LENGTH Partial Satisfaction Problems 32

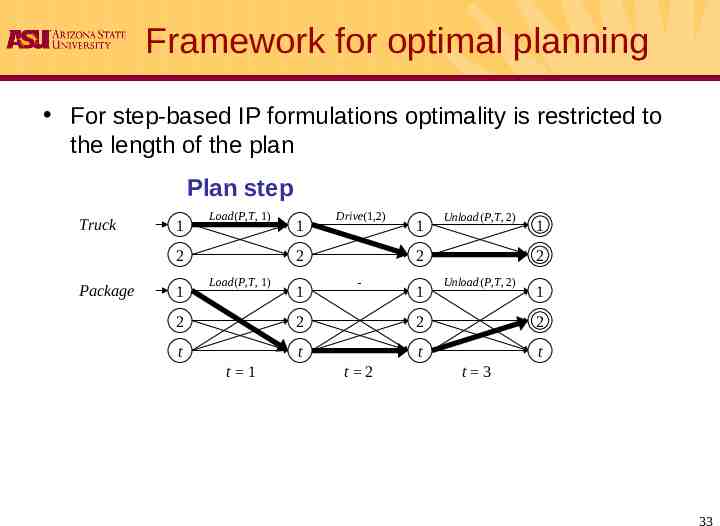
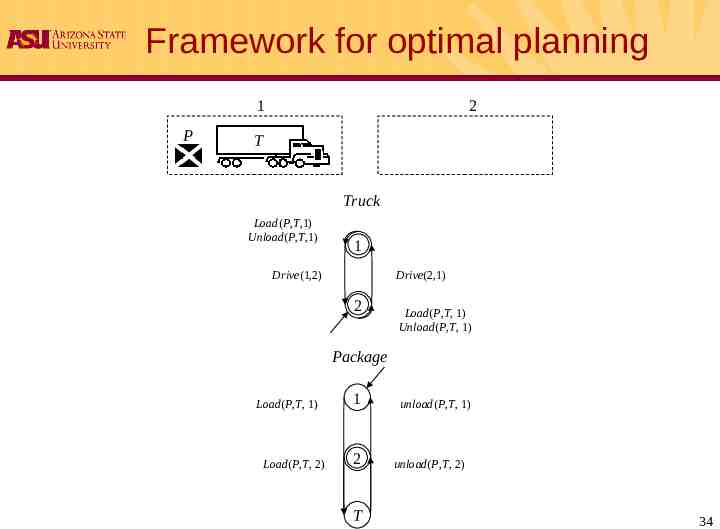
Framework for optimal planning For step-based IP formulations optimality is restricted to the length of the plan Plan step Truck 1 Load(P,T, 1) 2 Package 1 1 Drive(1,2) 2 Load(P,T, 1) 1 1 Unload(P,T, 2) 2 - 1 1 2 Unload(P,T, 2) 1 2 2 2 2 t t t t t 1 t 2 t 3 33

Framework for optimal planning 1 P 2 T Truck Load(P,T,1) Unload(P,T,1) 1 Drive(1,2) Drive(2,1) 2 Load(P,T, 1) Unload(P,T, 1) Package Load(P,T, 1) Load(P,T, 2) 1 2 T unload(P,T, 1) unload(P,T, 2) 34

Action selection formulation Variables – xa Z , for a A; xa is equal to the number of times action a is executed – y v(c,a) Z , for v V, a A, a –(c); y v(c,a) is equal to the number of times transition v(c,a) is executed No time indices No upper bounds Objective function – MIN a A caxa Constraints a v (e) y v(c,a) – a v–(e) y v(c,a) 1 –1 0 if c c0,v, c g if c c0,v, c g otherwise a v (e) y v(c,a) xa 35

Concurrent automata Given a set of state variables V {v1, , vn} For each v V we define a deterministic automaton Gv (Dv, Av, v, v, c0,v, gv) – Dv is a finite set of states corresponding to the domain of state variable v – Av is a finite set of actions associated with the transitions in Gv v : Dv A Dv is the transition function v : Dv 2A is the active action function – c0,v S is the initial state of state variable v – gv S is a set of goal states of state variable v 36

Parallel composition The parallel composition of the two automata G1 and G2 is the automaton G1 G2 : (D1 D2, A1 A2, 1 2, 1 2, (c0,1, c0,2), g1 g2) 1 2((c1,c2),a) : ( 1(c1,a), 2(c2,a) ( 1(c1,a), c2) (c1, 2(c2,a)) undefined if a 1(c1) 2(c2) if a 1(c1)\A2 if a 2(c2)\A1 otherwise 1 2(c1,c2) : [ 1(c1) 2(c2)] [ 1(c1)\A2] [ 2(c2)\A1] 37

Logistics example 1 P 2 T Truck Load(P,T,1) Unload(P,T,1) 1 Drive(1,2) Drive(2,1) 2 Load(P,T, 1) Unload(P,T, 1) Package Load(P,T, 1) Load(P,T, 2) 1 2 T unload(P,T, 1) unload(P,T, 2) 38

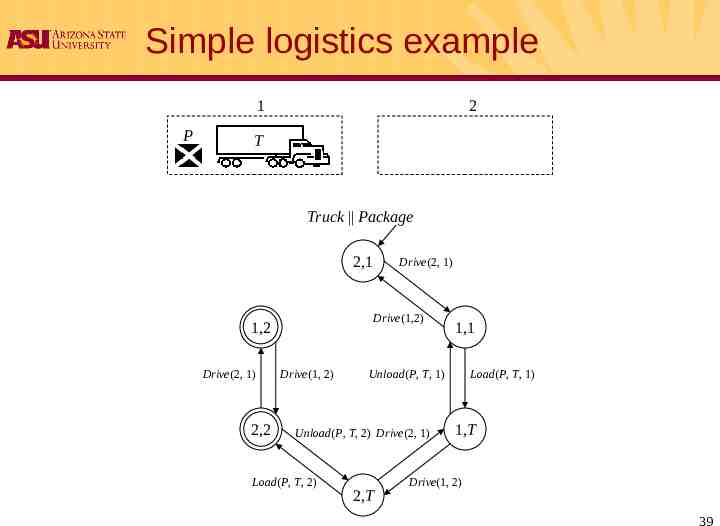
Simple logistics example 1 P 2 T Truck Package 2,1 Drive(1,2) 1,2 Drive(2, 1) 2,2 Drive(2, 1) Drive(1, 2) Unload(P, T, 1) Unload(P, T, 2) Drive(2, 1) Load(P, T, 2) 1,1 2,T Load(P, T, 1) 1,T Drive(1, 2) 39

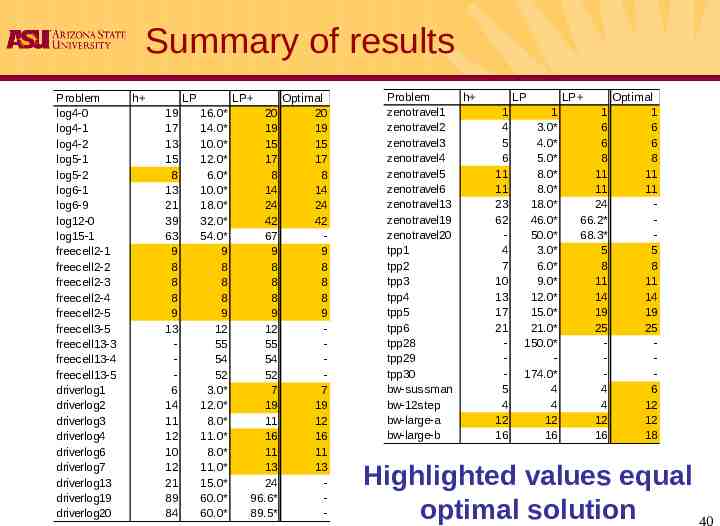
Summary of results Problem log4-0 log4-1 log4-2 log5-1 log5-2 log6-1 log6-9 log12-0 log15-1 freecell2-1 freecell2-2 freecell2-3 freecell2-4 freecell2-5 freecell3-5 freecell13-3 freecell13-4 freecell13-5 driverlog1 driverlog2 driverlog3 driverlog4 driverlog6 driverlog7 driverlog13 driverlog19 driverlog20 h LP 19 17 13 15 8 13 21 39 63 9 8 8 8 9 13 6 14 11 12 10 12 21 89 84 LP 16.0* 14.0* 10.0* 12.0* 6.0* 10.0* 18.0* 32.0* 54.0* 9 8 8 8 9 12 55 54 52 3.0* 12.0* 8.0* 11.0* 8.0* 11.0* 15.0* 60.0* 60.0* 20 19 15 17 8 14 24 42 67 9 8 8 8 9 12 55 54 52 7 19 11 16 11 13 24 96.6* 89.5* Optimal 20 19 15 17 8 14 24 42 9 8 8 8 9 7 19 12 16 11 13 - Problem h zenotravel1 zenotravel2 zenotravel3 zenotravel4 zenotravel5 zenotravel6 zenotravel13 zenotravel19 zenotravel20 tpp1 tpp2 tpp3 tpp4 tpp5 tpp6 tpp28 tpp29 tpp30 bw-sussman bw-12step bw-large-a bw-large-b LP 1 4 5 6 11 11 23 62 4 7 10 13 17 21 5 4 12 16 1 3.0* 4.0* 5.0* 8.0* 8.0* 18.0* 46.0* 50.0* 3.0* 6.0* 9.0* 12.0* 15.0* 21.0* 150.0* 174.0* 4 4 12 16 LP 1 6 6 8 11 11 24 66.2* 68.3* 5 8 11 14 19 25 4 4 12 16 Optimal 1 6 6 8 11 11 5 8 11 14 19 25 6 12 12 18 Highlighted values equal optimal solution 40

Summary of results 1000 100 h LP LP 10 1 0.1 0.01 Logistics Freecell Driverlog Zenotravel TPP Blocks 41

Utilize LP in heuristic search 400000 1200000 H LP H LP H LP RP H LP Cost RP UB 200000 600000 300000 0 0 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Zenotravel H LP Cost RP UB 100000 1 2 3 H LP RP 900000 Net benefit Net benefit 300000 1 3 5 7 9 11 13 15 17 19 Satellite 400000 H LP Net benefit 300000 H LP RP H LP Cost RP UB BBOP-LP planner 200000 100000 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Rovers [Benton, van den Briel, and Kambhampati, 2007] 42

Summary IP-based approaches do work – Optiplan, first IP-based planner to take part in the IPC series – Ranked 2nd in four out of seven domains in IPC4 in the optimal track for propositional domains IP-based approaches can compete with SAT-based approaches – Represent planning as a set of interdependent network flow problems – Generalize the notion of action parallelism Shift in focus towards optimal planning – Applied formulations to partial satisfaction planning problems – Developed a novel framework for optimal planning – Utilized LP relaxations in deriving quality sensitive heuristics 43

Publications status Journal Cited by 6 – [M.H.L. van den Briel, and S. Kambhampati. Optiplan: Unifying IP-based and graph-based planning. Journal of Artificial Intelligence Research, 24:623-635, 2005] – [M.H.L van den Briel, T. Vossen, and S. Kambhampati. Loosely coupled formulation for automated planning: An integer programming perspective. Journal of Artificial Intelligence Research, 31:217-257, 2008] – [(In progress) M.H.L van den Briel, T. Vossen, S. Kambhampati and J. Fowler. Optimal automated planning] Conference – [M.H.L. van den Briel, R. Sanchez, M.B. Do, and S. Kambhampati. Effective approaches for partial satisfaction (oversubscription) planning. In Proceedings of AAAI, pages 562-569, 2004] 15 – [M.H.L. van den Briel, T. Vossen, and S. Kambhampati. Reviving integer programming approaches for AI planning: A branch-and-cut framework. In Proceedings of ICAPS, pages 161-170, 2005] 3 – [M.B. Do, J. Benton, M.H.L. van den Briel, and S. Kambhampati. Planning with goal utility dependencies. In Proceedings of IJCAI, pages 1872-1878, 2007] 4 – [J. Benton, M.H.L. van den Briel, and S. Kambhampati. A hybrid linear programming and relaxed plan heuristic for partial satisfaction planning problems. In Proceedings of ICAPS, pages 24-41, 2007] 3 – [M.H.L. van den Briel, J. Benton, S. Kambhampati, and T. Vossen. An LP-based heuristic for optimal planning. In Proceedings of CP, pages 651-665, 2007] Cited by 31 Cited by Cited by Cited by Cited by 44

Publications status Cited by 5 Cited by 1 Cited by 1 Workshop and posters – [M.H.L. van den Briel, R. Sanchez, and S. Kambhampati. Over-Subscription in Planning: a Partial Satisfaction Problem. In Proceedings of ICAPS Workshop on Integrating Planning into Scheduling, 2005] – [M.H.L. van den Briel,. Kambhampati, and T. Vossen. Planning with numerical state variables through mixed integer programming. In Proceedings of ICAPS Poster Session, pages 5-8, 2005] – [M.H.L. van den Briel,. Kambhampati, and T. Vossen. Planning with preferences and trajectory constraints by integer programming. In Proceedings of ICAPS Workshop on Preferences and Soft Constraints in Planning, pages 19-22, 2006] – [J. Benton, M.H.L. van den Briel,. Kambhampati. Finding admissible bounds for oversubscription planning problems. In Proceedings of ICAPS Workshop on Heuristics for Domain-Independent Planning: Progress, Ideas, Limitations, Challenges, 2007] – [M.H.L. van den Briel,. Kambhampati, and T. Vossen. Fluent merging: A general technique to improve reachability heuristics and factored planning. In Proceedings of ICAPS Workshop on Heuristics for Domain-Independent Planning: Progress, Ideas, Limitations, Challenges, 2007] Citation count by Google Scholar 45