Information Networks Introduction to networks Lecture 1

Information Networks Introduction to networks Lecture 1

Announcement No Lecture this Thursday

Welcome! Introductions My name in finnish: Panajotis Tsaparas I am from Greece I graduated from University of Toronto In University of Helsinki for the past year Tutor: Evimaria Terzi Web searching and Link Analysis also Greek Knowledge of Greek is not required

Course overview The course goal Prerequisites: To read some recent and interesting papers on information networks Understand the underlying techniques Think about interesting problems Mathematical background on discrete math, graph theory, probabilities The course will be more “theoretical”, but your project may be more “practical” Style Both slides and blackboard

Topics Measuring Real Networks Models for networks Scale Free and Small World networks Distributed hashing and Peer-to-Peer search The Web graph Web crawling, searching and ranking Temporal analysis of data Gossip and Epidemics Clustering and classification Biological networks

Homework Two or three assignments of the following three types Project: Select your favorite network/algorithm/model and Reaction paper Problem Set Presentation do an experimental analysis do a theoretical analysis do a in-depth survey No final exam Final Grade: 50% assignments, 50% project (or 60%,40%) Tutorials: will be arranged on demand

Web page Web page has been (partially) updated http://www.cs.helsinki.fi/u/tsaparas/ InformationNetworks/

What is an information network? Network: a collection of entities that are interconnected A link (edge) between two entities (nodes) denotes an interaction between two entities We view this interaction as information exchange, hence, Information Networks The term encompasses more general networks

Why do we care about networks? Because they are everywhere Because they are growing more and more systems can be modeled as networks large scale problems Because we have the computational power to study them task: to develop the tools

Social Networks Links denote a social interaction Networks of acquaintances

Other Social networks actor networks co-authorship networks director networks phone-call networks e-mail networks IM networks Microsoft buddy network Bluetooth networks sexual networks

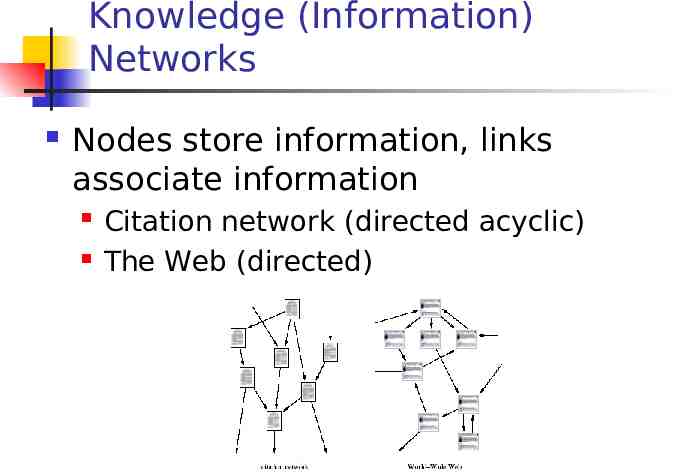
Knowledge (Information) Networks Nodes store information, links associate information Citation network (directed acyclic) The Web (directed)

Other Information Networks Peer-to-Peer networks Word networks Networks of Trust epinions

Technological networks Networks built for distribution of commodity The Internet router level AS level ISP network

The Internet The Opte Project

Other Technological networks Power Grids Airline networks Telephone networks Transportation Networks roads, railways, pedestrian traffic Software networks

Biological networks Biological systems represented as networks Protein-Protein Interaction Networks

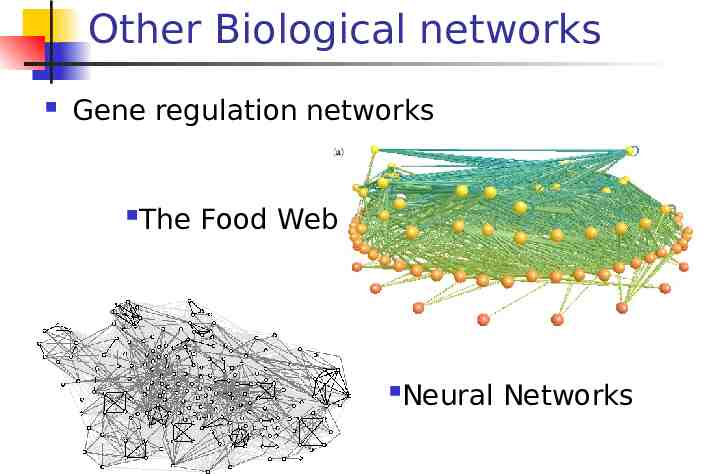
Other Biological networks Gene regulation networks The Food Web Neural Networks

Now what? The world is full with networks. What do we do with them? understand their topology and measure their properties study their evolution and dynamics create realistic models create algorithms that make use of the network structure

Mathematical Tools Graph theory Probability theory Linear Algebra

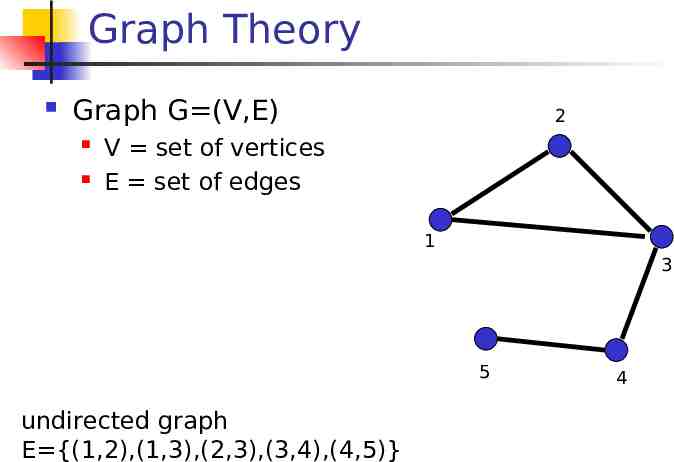
Graph Theory Graph G (V,E) 2 V set of vertices E set of edges 1 3 5 undirected graph E {(1,2),(1,3),(2,3),(3,4),(4,5)} 4

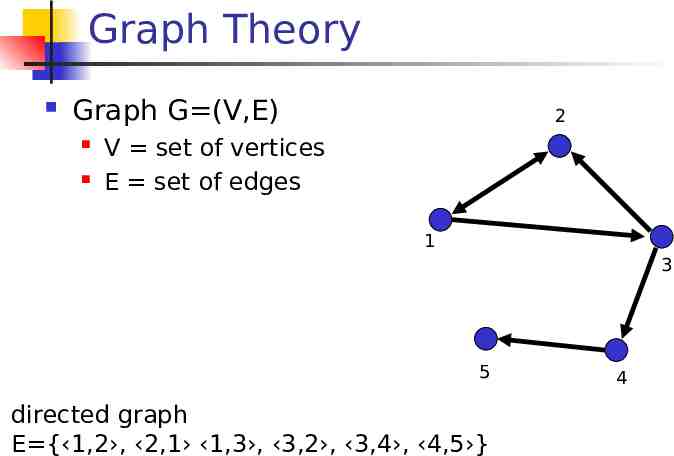
Graph Theory Graph G (V,E) 2 V set of vertices E set of edges 1 3 5 directed graph E {‹1,2›, ‹2,1› ‹1,3›, ‹3,2›, ‹3,4›, ‹4,5›} 4

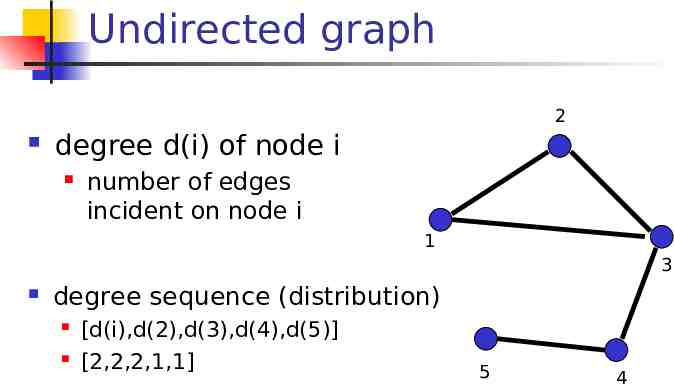
Undirected graph 2 degree d(i) of node i number of edges incident on node i 1 3 degree sequence (distribution) [d(i),d(2),d(3),d(4),d(5)] [2,2,2,1,1] 5 4

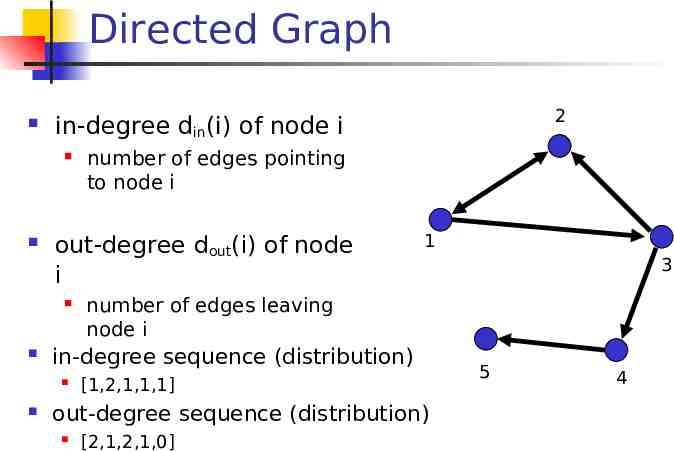
Directed Graph 1 [1,2,1,1,1] out-degree sequence (distribution) 3 number of edges leaving node i in-degree sequence (distribution) number of edges pointing to node i out-degree dout(i) of node i 2 in-degree din(i) of node i [2,1,2,1,0] 5 4

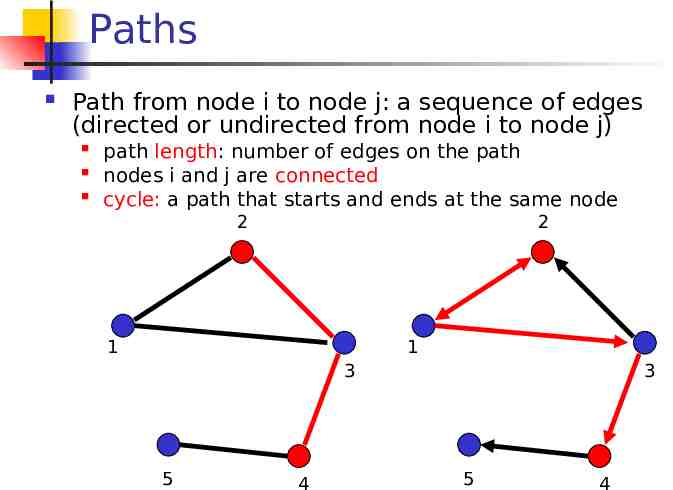
Paths Path from node i to node j: a sequence of edges (directed or undirected from node i to node j) path length: number of edges on the path nodes i and j are connected cycle: a path that starts and ends at the same node 2 2 1 1 3 5 4 3 5 4

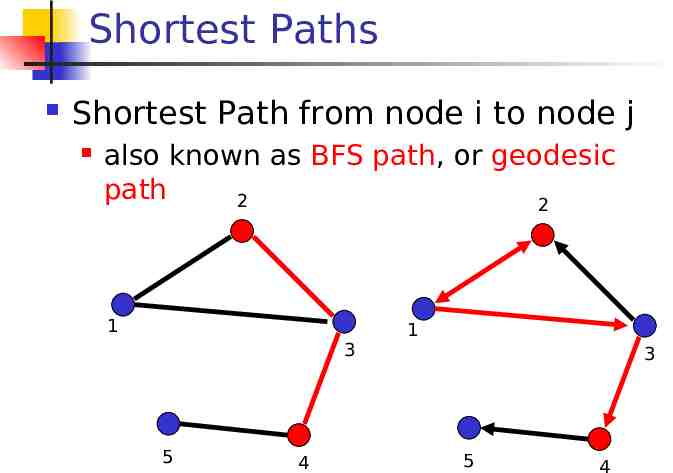
Shortest Paths Shortest Path from node i to node j also known as BFS path, or geodesic path 2 2 1 3 5 4 1 3 5 4

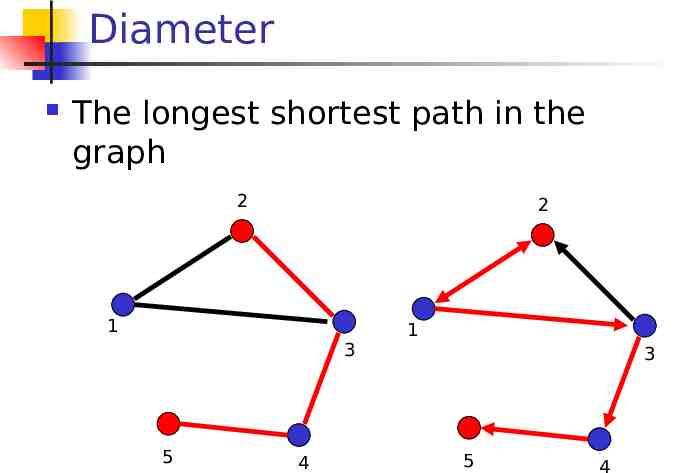
Diameter The longest shortest path in the graph 2 2 1 3 5 4 1 3 5 4

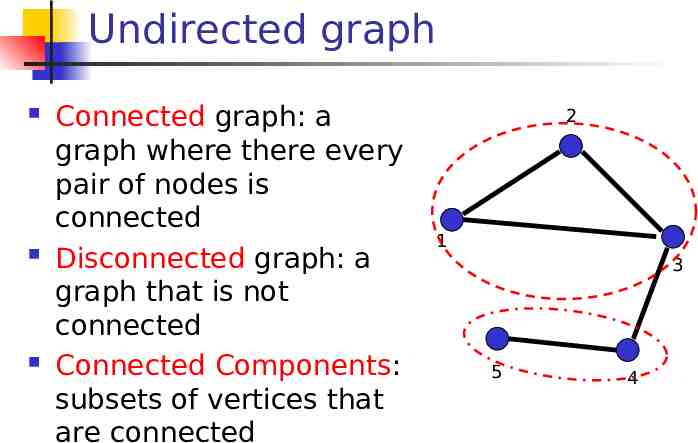
Undirected graph Connected graph: a graph where there every pair of nodes is connected Disconnected graph: a graph that is not connected Connected Components: subsets of vertices that are connected 2 1 3 5 4

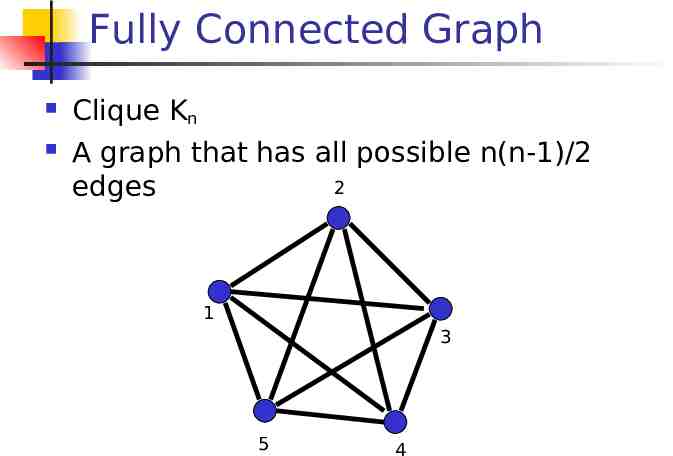
Fully Connected Graph Clique Kn A graph that has all possible n(n-1)/2 2 edges 1 3 5 4

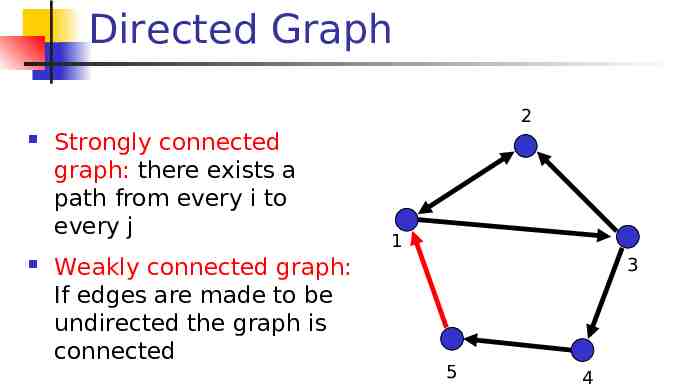
Directed Graph 2 Strongly connected graph: there exists a path from every i to every j Weakly connected graph: If edges are made to be undirected the graph is connected 1 3 5 4

Subgraphs Subgraph: Given V’ V, and E’ E, the graph G’ (V’,E’) is a subgraph of G. Induced subgraph: Given V’ V, let E’ E is the set of all edges between the nodes in V’. The graph G’ (V’,E’), is an induced subgraph of G 2 1 3 5 4

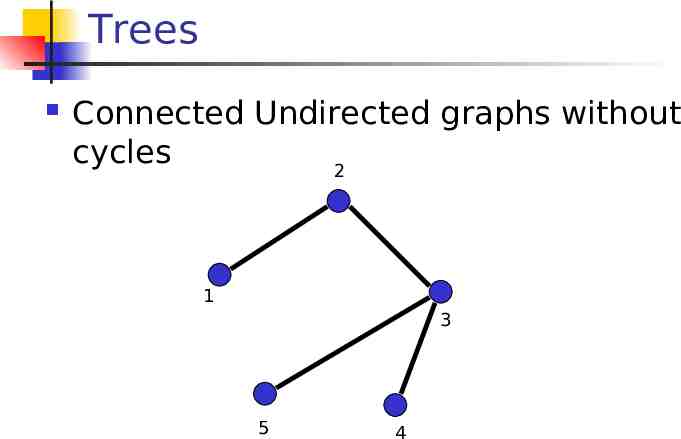
Trees Connected Undirected graphs without cycles 2 1 3 5 4

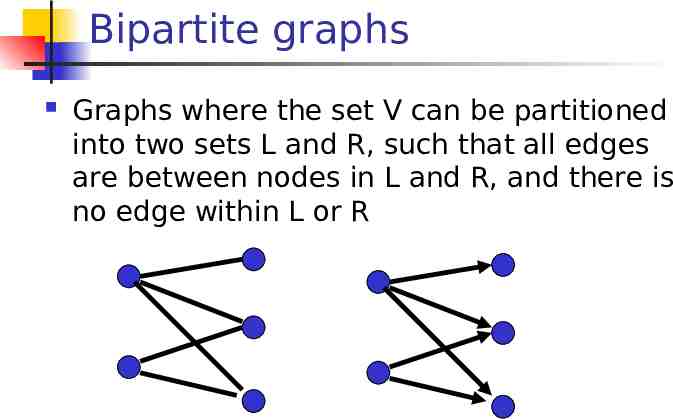
Bipartite graphs Graphs where the set V can be partitioned into two sets L and R, such that all edges are between nodes in L and R, and there is no edge within L or R

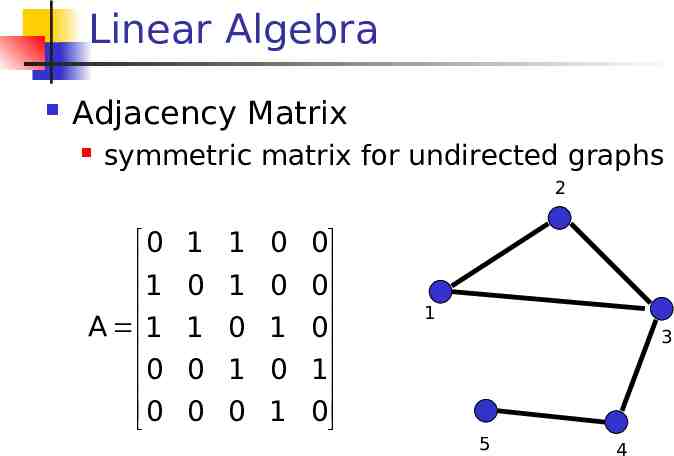
Linear Algebra Adjacency Matrix symmetric matrix for undirected graphs 2 0 1 A 1 0 0 1 1 0 0 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0 1 3 5 4

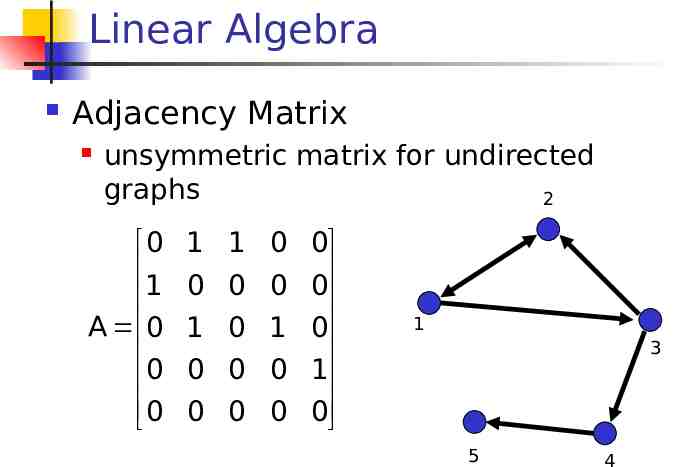
Linear Algebra Adjacency Matrix unsymmetric matrix for undirected graphs 2 0 1 A 0 0 0 1 1 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 1 3 5 4

Eigenvalues and Eigenvectors The value λ is an eigenvalue of matrix A if there exists a non-zero vector x, such that Ax λx. Vector x is an eigenvector of matrix A The largest eigenvalue is called the principal eigenvalue The corresponding eigenvector is the principal eigenvector Corresponds to the direction of maximum change

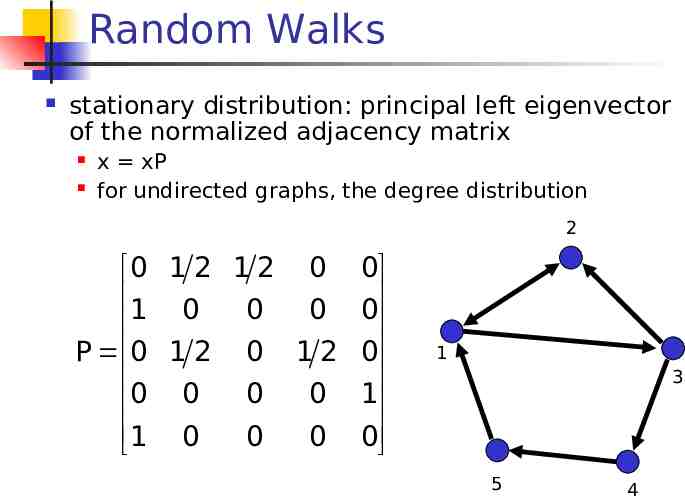
Random Walks Start from a node, and follow links uniformly at random. Stationary distribution: The fraction of times that you visit node i, as the number of steps of the random walk approaches infinity if the graph is strongly connected, the stationary distribution converges to a unique vector.

Random Walks stationary distribution: principal left eigenvector of the normalized adjacency matrix x xP for undirected graphs, the degree distribution 2 0 1 2 1 2 0 1 0 0 0 P 0 1 2 0 1 2 0 0 0 0 1 0 0 0 0 0 0 1 0 1 3 5 4

Probability Theory Probability Space: pair ‹Ω,P› Random variable X: Ω R Ω: sample space P: probability measure over subsets of Ω Probability mass function P[X x] Expectation E X xP[X x] x

Classes of random graphs A class of random graphs is defined as the pair ‹Gn,P› where Gn the set of all graphs of size n, and P a probability distribution over the set Gn Erdös-Renyi graphs: each edge appears with probability p when p 1/2, we have a uniform distribution

Asymptotic Notation For two functions f(n) and g(n) f(n) O(g(n)) if there exist positive numbers c and N, such that f(n) c g(n), for all n N f(n) Ω(g(n)) if there exist positive numbers c and N, such that f(n) c g(n), for all n N f(n) Θ(g(n)) if f(n) O(g(n)) and f(n) Ω(g(n)) f(n) o(g(n)) if lim f(n)/g(n) 0, as n f(n) ω(g(n)) if lim f(n)/g(n) , as n

P and NP P: the class of problems that can be solved in polynomial time NP: the class of problems that can be verified in polynomial time NP-hard: problems that are at least as hard as any problem in NP

Approximation Algorithms NP-optimization problem: Given an instance of the problem, find a solution that minimizes (or maximizes) an objective function. Algorithm A is a factor c approximation for a problem, if for every input x, A(x) c OPT(x) (minimization problem) A(x) c OPT(x) (maximization problem)

References M. E. J. Newman, The structure and function of complex networks, SIAM Reviews, 45(2): 167-256, 2003