HW2 Solutions
15 Slides55.50 KB
HW2 Solutions
Problem 1 Construct a bipartite graph where, every family represents a vertex in one partition, and table represents a vertex in another partition. There is a unit capacity edge between a family and a table. There is a source and a destination. The source has an edge to every family, and there is an edge from every table to the destination. Capacity of every source and family j edge equals the size of family j, and the capacity of every table – destination edge is the size of the table. A seating arrangement is possible iff the maximum flow equals the sum of the sizes of the families.
Problem 2 The commander is the source node. Add a destination node with infinite capacity edges from the vertices in S. The minimum effort equals the capacity of the min cut between the source and the destination, which equals the max flow from the source.
Problem 3 Assume that there is no infinite capacity path between the source and the destination. So, the flow in any link is upper bounded by the max flow, which is upper bounded by the sum of the capacities of the finite capacity links. So, the infinite capacities can be replaced by this number.
Problem 4 (1)False C 1, Flow 1 C 1000, Flow 100 C 1, Flow 1 C 1000, Flow 100 (2) True, Given any maxflow allocation subtract min of flow along forward edge, and flow along backward edge, from the flows in both these edges. The flow remains a maxflow, and the flow along the forward or the backward edge is 0.
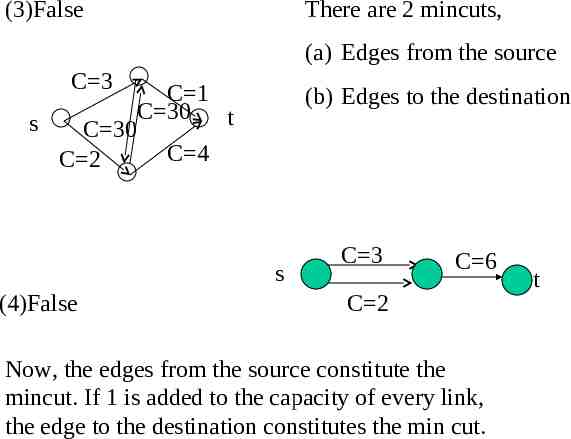
(3)False There are 2 mincuts, (a) Edges from the source C 3 C 1 C 30 t s C 30 C 4 C 2 (b) Edges to the destination s (4)False C 3 C 6 C 2 Now, the edges from the source constitute the mincut. If 1 is added to the capacity of every link, the edge to the destination constitutes the min cut. t
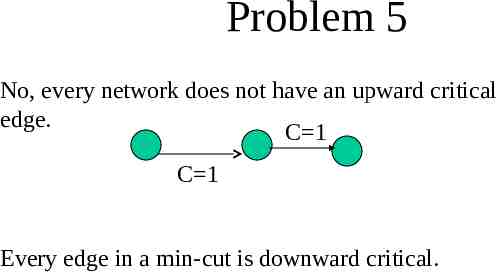
Problem 5 No, every network does not have an upward critical edge. C 1 C 1 Every edge in a min-cut is downward critical.
Problem 6 Find an augmenting path in the residual flow graph.
Problem 7 Let a and b be such that f(a) q, f(b) q. Need to show that f( a (1- )b) q. Follows from the fact that f( a (1- )b) f(a) (1- )f(b) q The first inequality follows from the convexity of f(x). ln ixi j j ln xi ln( j j xi) The last inequality follows from the convexity of –ln x
Problem 8 No, because r can always be increased in this range, without hurting any component (since none other exists). The answer is the same as in the first part. No, as one component can always be increased without hurting a smaller or equal component.
Problem 9 Construct a bipartite graph with faculties and courses representing vertices. There is an edge between two vertices only if one represents a faculty, and the other a course in the preference list of the faculty. Find a maximum matching in the bipartite graph. If the matching matches all the faculty vertices, a feasible allocation exists, otherwise not.
We need to find a feasible allocation where not more than k faculties get there second choices, if one exists. Now, every edge in the previous bipartite graph has a weight. Weight of a first priority edge is 1 Weight of a second priority edge is 1 is selected s.t. 0 1/M faculties) (M is the number of Suppose a feasible allocation exists. Then there is a matching with M edges.
A maximum weighted matching will always have M edges. Let, it have p M edges. Then its weight is at most p (1 ) p(1 1/M) p p/M p 1 p M Since there is a matching with M edges, and every edge has weight at least 1, we know that there is a matching with weight at least 1. So, a maximum weighted matching will always choose a feasible allocation. Since it is a maximum weighted matching, it must choose as many first priority edges (weight 1 ) as possible, on top of choosing a matching with M edges. Thus it will choose a k-feasible one if it exists.
Problem 10 Assign new weights to all edges. First choose the edges with the highest weight among the old weights. Give them weight 1. Now choose the edges with second highest old weight. New weight of each of these is the sum of the new weights of all edges whose new weights have been assigned. Now choose the third highest ones, and the new weights equal the sum of the previous new weights, etc .
A maximum weighted matching gives absolute priority to the least old weights (because their weights are very high now), subject to that highest priority to the second lowest old weights etc . So, a max weighted matching gives a lexicographically maximum matching.