Homework 5 Statistics Minimum Value Maximum Value Range Average

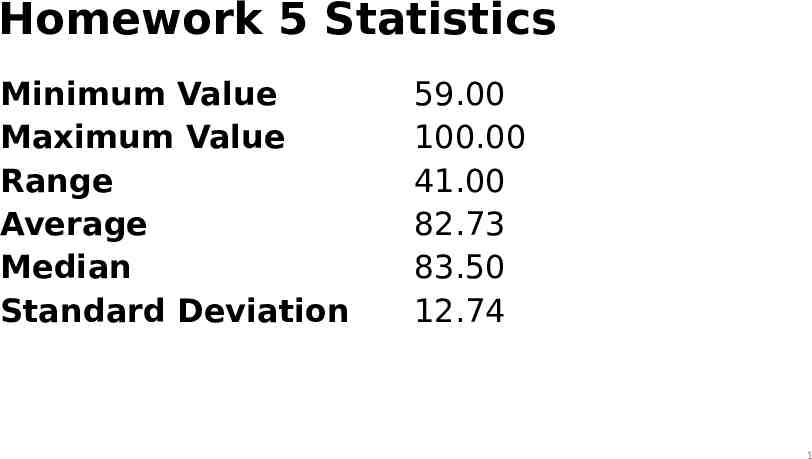
Homework 5 Statistics Minimum Value Maximum Value Range Average Median Standard Deviation 59.00 100.00 41.00 82.73 83.50 12.74 1

Course Evaluation Please Complete Your Course Evaluations Your feedback is valuable! Homework 5 Solutions and Practice Final Available on Piazza 2

Final Exam Time: Tuesday, December 11th at 8AM Location: LWSN B151 Comprehensive but heavier coverage of material covered in second half of semester Format Multiple choice Fill in the blank (expect more of these questions) true/false/more information Practice Exam on Piazza Solutions to practice exam distributed on Thursday (Do not distribute!) 3

Review: Attacker Models Passive Eavesdropping Attacker (Eve) Active Attacker Chosen Plaintext Attack: Attacker can control/influence messages that are encrypted Chosen Ciphertext Attack: Attacker can convince honest party to (partially) decrypt ciphertexts of his/her choosing. MPC: Semi-Honest vs Malicious Man-In-The-Middle Attacker 4

Review: Key Concepts for Symmetric Key Crypto Building Blocks: OWFs, OWPs, PRGs, PRFs, CRHFs, PRPs (Block Cipher) Constructions: PRFs from PRGs, PRPs via Feistel Network etc Should understand syntax (e.g., PRF uses a key, but a PRG doesn’t) and security definitions (e.g., PRG vs PRF) MAC vs. Encryption Confidentiality vs Integrity Syntax Security Definition(s): Authenticated Encryption, CCA-Security, CPA-Security Perfect Secrecy, MAC-forgery game 5

Review: Collision Resistant Hash Functions (CRHF) CRHFs are a unique object in cryptography No secret key (public seed) --- security definition (e.g., seeded) vs practice (e.g., SHA3) Davies-Meyer construction in Ideal Cipher Model Handling long inputs Merkle Tree Merkle-Damgård Collision/Inversion Attacks Birthday Attack Small Space Birthday Attack Pre-Computation Attacks (Time/Space Tradeoffs) Random Oracle Methodology 6

Review: Key Principles Sufficient Key Space Principle Resist brute-force attacks Penguin Principle Issues with stateless/deterministic encryption schemes Importance of nonces Independent Key Principle 7

Review: Asymmetric Key Crypto Key Assumptions: FACTORING RSA-Inversion Problem Discrete Logarithm Problem DDH vs CDH OWFs (for Certain Signature Schemes) Public Key Encryption Syntax Security Definition(s): CPA vs CCA-security Constructions: Plain RSA, El Gamal, RSA-OAEP Key Encapsulation Mechanism (and how to use them) 8

Review: Signatures Goal: Message Integrity Signature Properties: Public Verification Transferrable: Bob receives signature from Alice and can forward to Joe Can identify sender Cannot identify intended recipient Example: Alice signs message “I promise to pay you 50” and sends to Bob Eve can copy signature and forward to Joe who believes that Alice will pay him 50. Solution: Can bind signature to recipient, by indicating recipient inside the message E.g., “I promise to pay you (Bob) 50” Contrast with MAC Need secret key for verification Cannot identify sender (anyone who has secret key) 9

Review: Signatures and MACs What are some secure constructions of signatures? RSA-FDH Schnorr-Signatures (Fiat-Shamir) DSA/ECDSA How to build a MAC? HMAC PRF: t Fk(m) Handling Long Messages: Hash and sign/mac How to build an (in)secure signature/MAC scheme? 10

Review: Multi-Party Computation Malicious vs Semi-Honest Security Models Security Definition (Simulator) Captures intuition that Alice learns “nothing else” about Bob’s input Yao’s Protocol (Garbled Circuits) What is security model? Building Blocks: Oblivious Transfer, CPA-Secure Encryption Use of Zero-Knowledge Proofs in MPC 11

Review: Zero-Knowledge Decision Problem (e.g., DDH, SAT, CLIQUE) Properties Completeness Honest prover can always get verifier to accept a true statement Soundness A cheating prover can’t consistently get honest verifier to accept Zero-Knowledge How to build a simulator? Interactive vs Non-Interactive Zero-Knowledge 12

Practice Problem 1: NIZK Build a NIZK for the group membership problem Verifier: Knows h, wants to be sure that h is in g Prover: Knows x such that h gx Prover picks r and sets Prover selects the challenge b LSB(H(z)), and sets the response R r bx. Prover outputs the proof (z,R) Verifier computes b LSB(H(z)) and checks that Problem? 13

Practice Problem 1: NIZK (FIX) Build a NIZK for the group membership problem Verifier: Knows h, wants to be sure that h is in g Prover: Knows x such that Prover picks and sets Prover selects the challenge and sets the responses . Prover outputs the proof (,R1), ,(,Rk) Verifier computes and checks that for each i. How to build the simulator? 14

Practice Problem 2: Better Soundness Build an (interactive) Zero-Knowledge Proof for the group membership problem with soundness instead of k. Verifier: Knows h, wants to be sure that h is in g Prover: Knows such that Protocol: 1. Prover picks and sets for each i. 2. Verifier selects the challenge 3. Prover computes the responses . 4. Verifier checks that for each i. How to build the simulator? 15

Practice Problem 2: Better Soundness in ZK Protocol: 1. Prover picks r1, ,rk and sets for each i. 2. Verifier selects the challenge b1, ,bk 3. Prover computes the responses Ri ri bix. 4. Verifier checks that for each i. Trick Question! Simulator should not be able to output NIZK for claim (without tampering with random oracle) Dishonest verifier can set b1, ,bk H(z1, ,zk) to obtain NIZK proof ! 16

Practice Problem 2: Better Soundness in ZK Protocol 2: 1. Verifier selects nonce b and sends y H(b) to the prover. 2. Prover picks r1, ,rk and sets for each i. 3. Verifier reveals b and sets challenges b1, ,bk b 4. Prover computes the responses Ri ri bix. 5. Verifier checks that for each i. 17

Practice Problem 3: Garbled Circuit Reuse Let f(a1,a2,b1,b2) (a1 AND b1) OR (a2 AND b2) Alice sends Bob a Garbled Circuit with keys Keys and for each input/output wire W. Suppose Alice first runs the protocol with input (0,1) and Bob’s input (1,1) Which keys can Bob recover during the protocol? , , , (initial inputs), , (AND gates), (output) Later suppose Alice runs the protocol with new input (1,0) but does not regarble the circuit (Bob’s input is the same) What keys can Bob recover after second iteration? Answer: Every key except for , 18

Practice Problem 4: RSA Authentication RSA Based Authentication Verifier sends random nonce r mod N to Prover Prover authenticates with R rd mod N Verifier checks that Re r mod N What would security definition look like for generic authentication protocol? Define the game Is this protocol secure? Yes (assuming RSA-Inversion assumption) 19

Practice Problem 5: RSA Overuse RSA Based Authentication Verifier sends random nonce r mod N to Prover Prover authenticates with R rd mod N Verifier checks that Re r mod N Suppose we use the same secret key e for Key Encapsulation and for RSA Authentication? KEM: outputs (y,K H(x)) where y xe mod N What could go wrong? 20

Cryptography CS 555 Week 16: Zero-Knowledge Proofs, Hot Topics in Cryptography Review for Final Exam Readings: Katz and Lindell Chapter 10 & Chapter 11.1-11.2, 11.4 Fall 2018 21

CS 555:Week 15: ZeroKnowledge Proofs 22

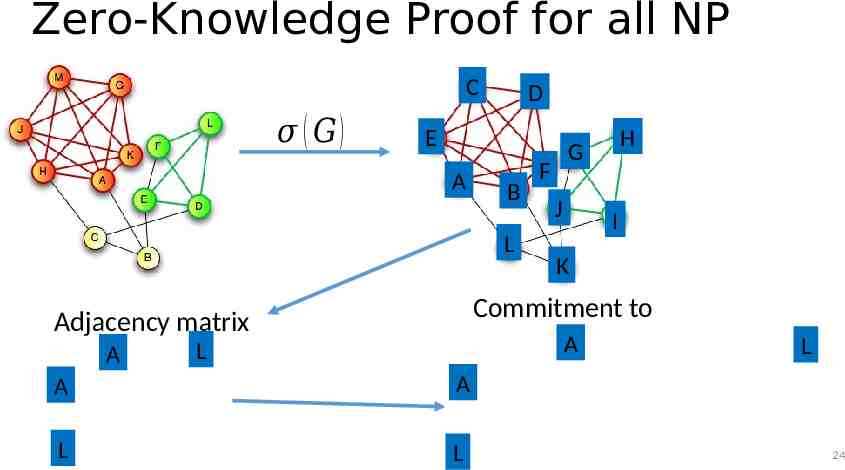
Zero-Knowledge Proof for all NP CLIQUE Input: Graph G (V,E) and integer k 0 Question: Does G have a clique of size k? CLIQUE is NP-Complete Any problem in NP reduces to CLIQUE A zero-knowledge proof for CLIQUE yields proof for all of NP via reduction Prover: Knows k vertices v1, ,vk in G (V,E) that form a clique 23

Zero-Knowledge Proof for all NP C 𝜎 ( 𝐺) D E A B L G F J I K Commitment to Adjacency matrix A H A L A A L L L 24

C D Zero-Knowledge Proof for allE NP Prover: Knows k vertices v1, ,vk in G (V,E) that for a clique 1. 2. 3. 4. Prover selects a permutation over V Prover commits to the adjacency matrix of (G) Verifier sends challenge c (either 1 or 0) If c 0 then prover reveals and adjacency matrix A B L H G F J I K 1. Verifier confirms that adjacency matrix is correct for (G) 5. If c 1 then prover reveals the submatrix formed by first rows/columns of corresponding to 1. Verifier confirms that the submatrix forms a clique. 25

Soundness and Completeness Completeness: If the prover knows a clique he can always respond to the challenge. Soundness: If no clique exists then either 1. The prover commits to (permutation of) the original graph Cannot respond to challenge (c 1) to reveal submatrix containing clique 2. The prover commits to a different (not-isomorphic) graph Cannot respond to challenge to reveal permutation 26

Zero-Knowledge Proof Simulator if b 0 𝒄𝒉𝒂𝒍𝒍𝒆𝒏𝒈𝒆 𝒄 𝑽 ′ (𝑮,𝐶𝑜𝑚 ( 𝐴 )) { 𝟎,𝟏 } Response Dishonest (verifier); , 𝑫𝒆𝒄𝒊𝒔𝒊𝒐𝒏 𝒅 𝑽 ′ (𝑮 ,𝐶𝑜𝑚 ( 𝐴) ,𝒄 ,𝒓 ) Zero-Knowledge: For all PPT V’ exists PPT Sim s.t Simulator Cheat bit b, , A (random ) 27

Zero-Knowledge Proof Simulator if b 0 𝒄𝒉𝒂𝒍𝒍𝒆𝒏𝒈𝒆 𝒄 𝑽 ′ (𝑮,𝐶𝑜𝑚 ( 𝐴 )) { 𝟎,𝟏 } Dishonest (verifier); , 𝑫𝒆𝒄𝒊𝒔𝒊𝒐𝒏 𝒅 𝑽 ′ (𝑮 ,𝐶𝑜𝑚 ( 𝐴) ,𝒄 ,𝒓 ) Zero-Knowledge: For all PPT V’ exists PPT Sim s.t Simulator Cheat bit b, , A (random ) 28

Zero-Knowledge Proof for all NP Completeness: Honest prover can always make honest verifier accept Soundness: If prover commits to adjacency matrix of (G) and can reveal a clique in submatrix of then G itself contains a k-clique. Proof invokes binding property of commitment scheme. Zero-Knowledge: Simulator cheats and either commits to wrong adjacency matrix or cannot reveal clique. Repeat until we produce a successful transcript. Indistinguishability of transcripts follows from hiding property of commitment scheme. 29

Secure Multiparty Computation (Adversary Models) Semi-Honest (“honest, but curious”) All parties follow protocol instructions, but dishonest parties may be curious to violate privacy of others when possible Fully Malicious Model Adversarial Parties may deviate from the protocol arbitrarily Quit unexpectedly Send different messages It is much harder to achieve security in the fully malicious model Convert Secure Semi-Honest Protocol into Secure Protocol in Fully Malicious Mode? Tool: Zero-Knowledge Proofs Prove: My behavior in the protocol is consistent with honest party 30

CS 555:Week 15: Hot Topics 31

Shor’s Algorithm Quantum Algorithm to Factor Integers Running Time O((log N)2(log log N)(log log log N)) Building Quantum Circuits is challenging, but. RSA is broken if we build a quantum computer Current record: Factor 21 3x7 with Shor’s Algorithm Source: Experimental Realisation of Shor’s Quatum Factoring Algorithm Using Quibit Recycling (https://arxiv.org/pdf/1111.4147.pdf) https://en.wikipedia.org/wiki/Shor%27s algorithm

Quantum Resistant Crypto Symmetric key primitives are believed to be safe but Grover’s Algorithm does speed up brute-force attacks significantly () Solution: Double Key Lengths Integer Factoring, Discrete Log and Elliptic Curve Discrete Log are not safe All public key encryption algorithms we have covered are unsafe RSA, RSA-OAEP, El-Gamal, . https://en.wikipedia.org/wiki/Lattice-based cryptography

Post Quantum Cryptography Symmetric key primitives are believed to be safe but Grover’s Algorithm does speed up brute-force attacks significantly () Solution: Double Key Lengths Hashed Based Signatures are believed to be safe Lamport One-Time Signatures and extensions to many-time signatures Lattice Based Cryptography is a promising approach for Quantum Resistant Public Key Crypto Ring-LWE NTRU https://security.googleblog.com/2016/07/experimenting-with-post-quantum.html

Fully Homomorphic Encryption (FHE) Idea: Alice sends Bob and Bob cannot decrypt messages, but given a circuit C can compute Bob has and can also include his own encrypted inputs Many Applications: Export confidential computation to cloud Secure Multiparty Computation, https://simons.berkeley.edu/talks/shai-halevi-2015-05-18a (Lecture by Shai Halevi)

Fully Homomorphic Encryption (FHE) Idea: Alice sends Bob Bob cannot decrypt messages, but given a circuit C can compute We now have candidate constructions! Encryption/Decryption are polynomial time but expensive in practice. Proved to be CPA-Secure under plausible assumptions Remark 1: Partially Homomorphic Encryption schemes cannot be CCASecure. Why not? https://simons.berkeley.edu/talks/shai-halevi-2015-05-18a (Lecture by Shai Halevi)

Partially Homomorphic Encryption Plain RSA is multiplicatively homomorphic But not additively homomorphic Pallier Cryptosystem Not same as FHE, but still useful in multiparty computation https://en.wikipedia.org/wiki/Paillier cryptosystem

Partially Homomorphic Encryption Secret Key: Large (prime) number p. Public Key: for each where Encrypting a Bit : Select Random Subset: and random Return Decrypting a ciphertext: As long as p 38

Partially Homomorphic Encryption Encrypting a Bit : Select Random Subset: and random Return Adding two ciphertexts Noise increases a bit 39

Partially Homomorphic Encryption Encrypting a Bit : Select Random Subset: and random Return Multiply two ciphertexts Noise increases a bit more (multiplicative) 40

Bootstrapping (Gentry 2009) Transform Partially Homomorphic Encryption Scheme into Fully Homomorphic Encryption Scheme Key Idea: Maintain two public keys pk1 and pk2 for partially homomorphic encryption Also, encrypt sk1 using pk2 and encrypt sk2 under pk1 The ciphertexts are included in the public key Run homomorphic evaluation using pk1 until the noise gets to be too large Let c1, ,ck be intermediate ciphertext(s) (under key pk1) Encrypt c1, ,ck bit by bit under (under key pk2) Then evaluate the decryption circuit homorphically (under key pk2) Challenge: Need to make sure that decryption circuit is shallow enough to evaluate Expensive, but there are tricks to reduce the running time 41

Fully Homomorphic Encryption Resources Implementation: https://github.com/shaih/HElib Tutorial: https://www.youtube.com/watch?v jIWOR2bGC7c 42

Program Obfuscation (Theoretical Cryptography) Program Obfuscation Idea: Alice obfuscates a circuit C and sends C to Bob Bob can run C, but cannot learn “anything else” Lots of applications Indistinguishability Obfuscation “Best Possible Obfuscation” cannot distinguish O(C) from O(C’) when C C’ compute the same function Theoretically Possible In the sense that is technically polynomial time Secure Hardware Module (e.g., SGX) can be viewed as a way to accomplish this in practice Must trust third party (e.g., Intel) https://simons.berkeley.edu/talks/amit-sahai-2015-05-19a (Lecture by Amit Sahai)

Differential Privacy

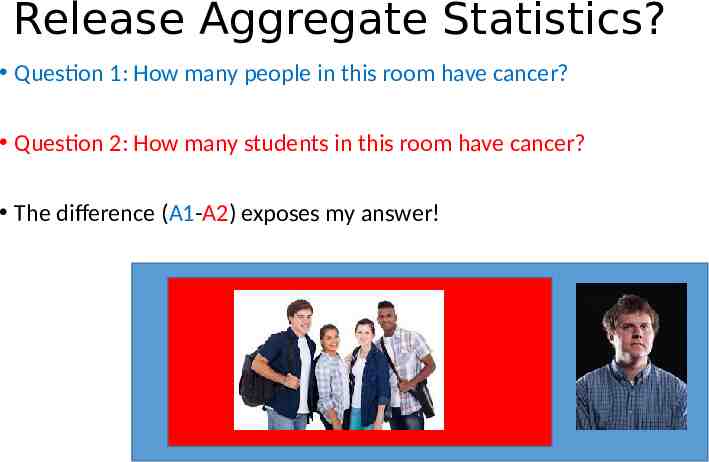
Release Aggregate Statistics? Question 1: How many people in this room have cancer? Question 2: How many students in this room have cancer? The difference (A1-A2) exposes my answer!

Differential Privacy: Definition n people Neighboring datasets: Name CS Prof? STD? Name CS Prof? STD? Replace x with x’ J Blocki [DMNS06, DKMMN06] Bjork 1 -1 -1 ? D D’ 46

Differential Privacy vs Cryptography is not negligibly small. We are not claiming that, when D and D’ are neighboring datasets, Otherwise, we would have for any two data-sets X and Y. Why? Cryptography Insiders/Outsiders Only those with decryption key(s) can reveal secret Multiparty Computation: Alice and Bob learn nothing other than f(x,y) 47

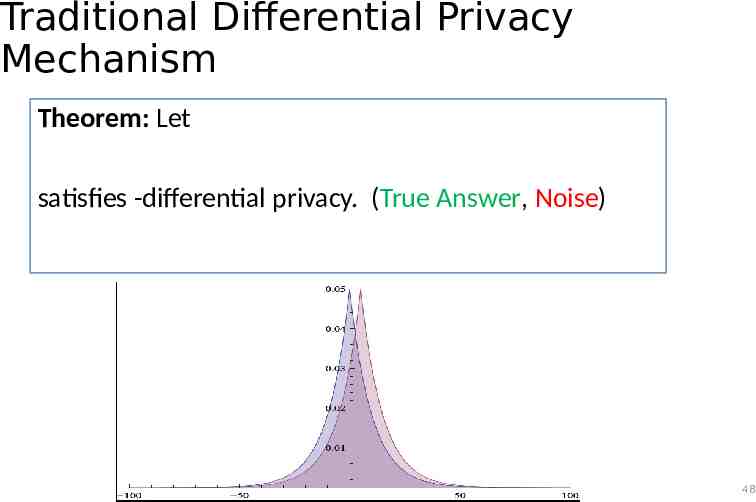
Traditional Differential Privacy Mechanism Theorem: Let satisfies -differential privacy. (True Answer, Noise) 48

Traditional Differential Privacy Mechanism Theorem: Let Observe: satisfies -differential privacy. (True Answer, Noise) True Answer for Dataset True Answer for Adjacent Dataset 19 0 𝜀 Pr [ A ( D ′ ) 20] 𝑒 20 0 𝜀 Pr [ A ( D ) 20] 𝑒 49

Resources 99 Free PDF: https://www.cis.upenn.edu/ aaroth/Papers/privacybook.pdf

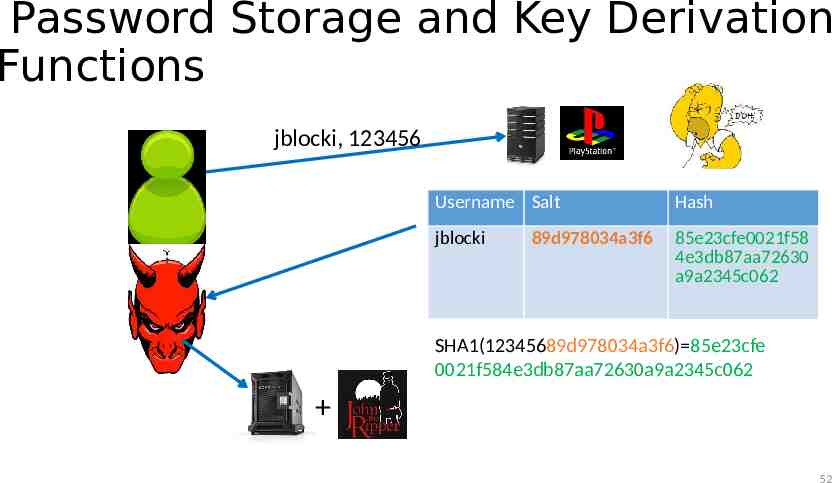
Password Storage and Key Derivation Functions jblocki, 123456 Username Salt Hash jblocki 85e23cfe0021f58 4e3db87aa72630 a9a2345c062 89d978034a3f6 SHA1(12345689d978034a3f6) 85e23cfe 0021f584e3db87aa72630a9a2345c062 52

Offline Attacks: A Common Problem Password breaches at major companies have affected millions billions of user accounts.

Offline Attacks: A Common Problem Password breaches at major companies have affected millions billions of user accounts.

Goal: Moderately Expensive Hash Function Fast on PC and Expensive on ASIC?

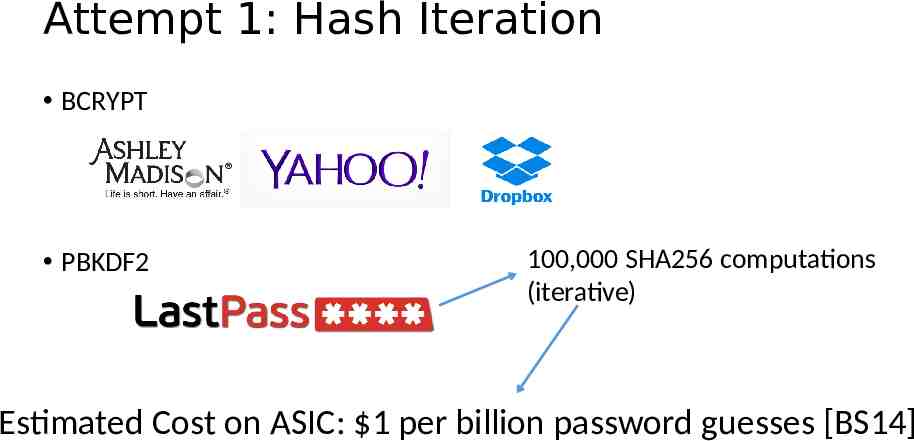
Attempt 1: Hash Iteration BCRYPT PBKDF2 100,000 SHA256 computations (iterative) Estimated Cost on ASIC: 1 per billion password guesses [BS14]

USD Co st S HA 25 6 User Patience Time Disclaimer: This slide is entirely for humorous effect. Standard Patience Units The Challenge

Memory Hard Function (MHF) Intuition: computation costs dominated by memory costs vs. Data Independent Memory Hard Function (iMHF) Memory access pattern should not depend on input

(2013-2015) https://password-hashing.net/

We recommend that you use Argon2 (2013-2015) https://password-hashing.net/

We recommend that you use Argon2 (2013-2015) https://password-hashing.net/ There are two main versions of Argon2, Argon2i and Argon2d. Argon2i is the safest against sidechannel attacks

Depth-Robustness: The Key Property Necessary [AB16] and sufficient [ABP16] for secure iMHFs

Question Are existing iMHF candidates based on depthrobust DAGs?

Answer: No

Can we build a secure iMHF? Github: https://github.com/Practical-Graphs/Argon2-Practical-Graph