GAME THEORY

GAME THEORY

Game Theory and Economics Game theory is the study of how people behave in strategic situations. Strategic decisions are those in which each person, in deciding what actions to take, must consider how others might respond to that action.

Game Theory and Economics If the market is composed by a small number of firms, each firm must act strategically. Each firm affects the market price changing the quantity produced. Suppose 2 firms are producing 100 units. If one of the firms decides to increase the production by 10 units. The market supply will increase from 200 to 210 and the price has to drop to reach an equilibrium.

Game Theory and Economics Therefore, it also affects the profits of other firms. Each firm knows that its profit depends not only on how much it produced but also on how much the other firms produce.

What is a Game? A game is a situation where the participants’ payoffs depend not only on their decisions, but also on their rivals’ decisions. This is called Strategic Interactions: My optimal decisions will depend on what others do in the game.

A Game Four elements to describe a game: players; rules: when each player moves, what are the possible moves, what is known to each player before moving; outcomes of the moves; payoffs of each possible outcome: how much money each player receive for any specific outcome.

Matching pennies Each player selects one side of a coin; if the coins match player 1 wins and gets 1 dollar from player 2; if the coins don’t match player 2 wins and gets 1 dollar from player 1.

Matrix Representation of Matching Pennies Player 2 Head Tail Head 1,-1 -1,1 Tail -1,1 1,-1 Player 1

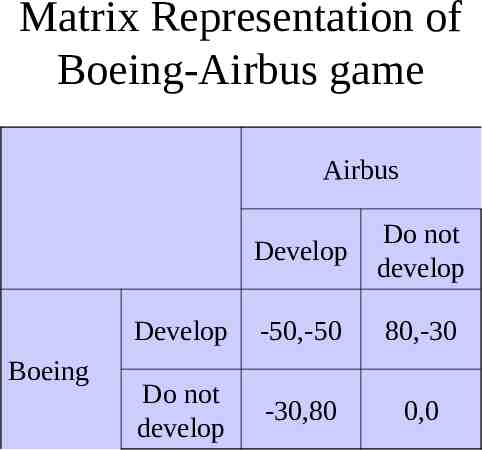
Boeing-Airbus game Boeing and Airbus have to decide whether to invest in the development of a Super Jumbo for long distance travel; if they both develop successfully the new plane, their profits will drop by 50 millions a year; if only one develop the Super Jumbo, it will make 80 millions a year in additional profits, whereas the profits of the other firm will drop by 30 millions a year; if no firm develops the plane, nothing changes.

Matrix Representation of Boeing-Airbus game Airbus Boeing Develop Do not develop Develop -50,-50 80,-30 Do not develop -30,80 0,0

Solutions of the Games To predict what will be the solution/outcome of the game we need some tools: dominated and dominant strategies; Nash equilibrium.

Prisoners Dilemma Two individuals have been arrested for possession of guns. The police suspects that they have committed 10 bank robberies; if nobody confesses the police, they will be jailed for 2 years. if only one confesses, she’ll go free and her partner will be jailed for 40 years. if they both confess, they get 16 years

Matrix Representation of Prisoners Dilemma Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 40,0 2,2

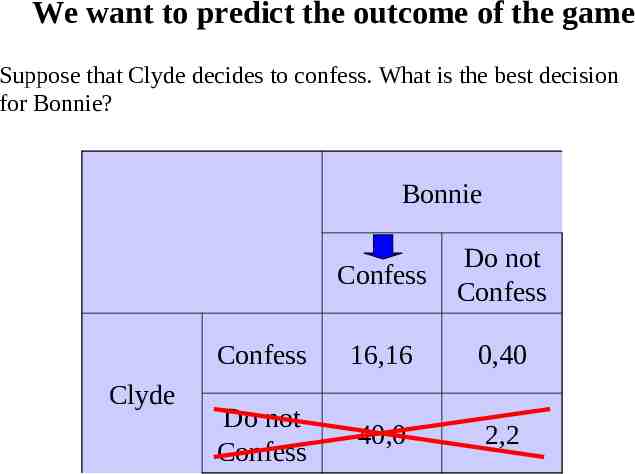
We want to predict the outcome of the game Suppose that Clyde decides to confess. What is the best decision for Bonnie? Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 40,0 2,2

We want to predict the outcome of the game Suppose that Clyde decides to remain silent. What is the best decision for Bonnie? Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 40,0 2,2

Dominated and Dominant Strategy Dominant Strategy: a strategy that gives higher payoffs no matter what the opponent does; Dominated Strategy: a strategy is dominated if there exists another strategy that is dominant. So far we have only assumed that each player is rational to determine the outcome of the game.

We want to predict the outcome of the game Suppose that Bonnie decides to confess. What is the best decision for Clyde? Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 40,0 2,2

We want to predict the outcome of the game Suppose that Bonnie decides to remain silent. What is the best decision for Clyde? Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 40,0 2,2

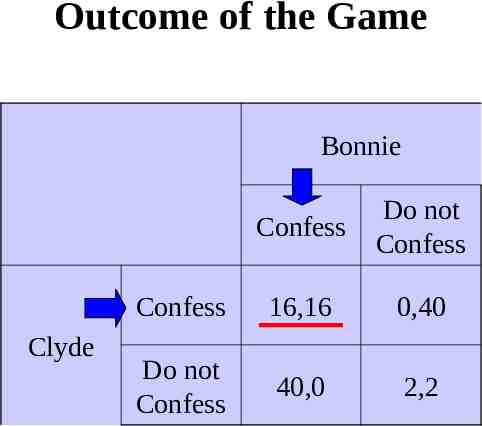
Outcome of the Game Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 40,0 2,2

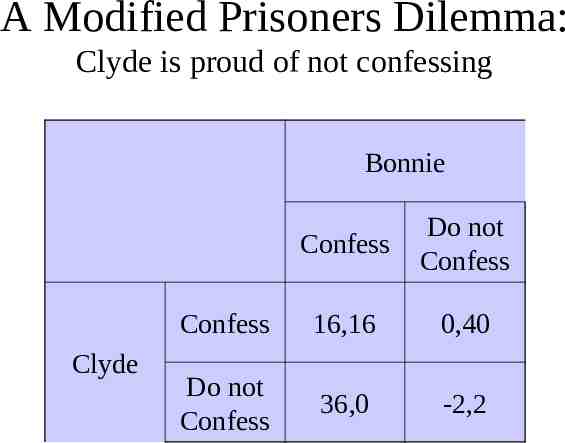
A Modified Prisoners Dilemma: Clyde is proud of not confessing Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 36,0 -2,2

We want to predict the outcome of the game Suppose that Bonnie decides to confess. What is the best decision for Clyde? Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 36,0 -2,2

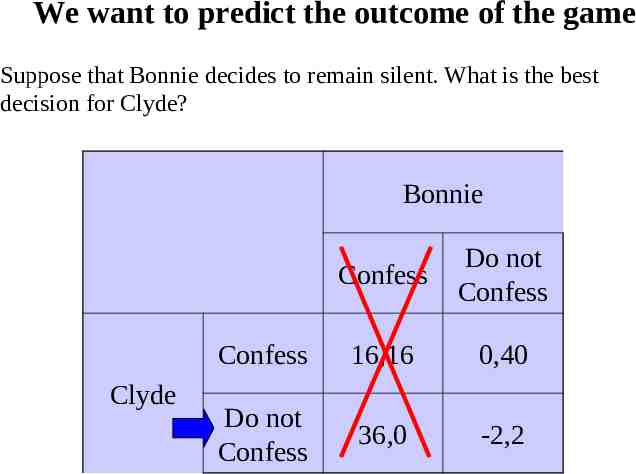
We want to predict the outcome of the game Suppose that Bonnie decides to remain silent. What is the best decision for Clyde? Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 36,0 -2,2

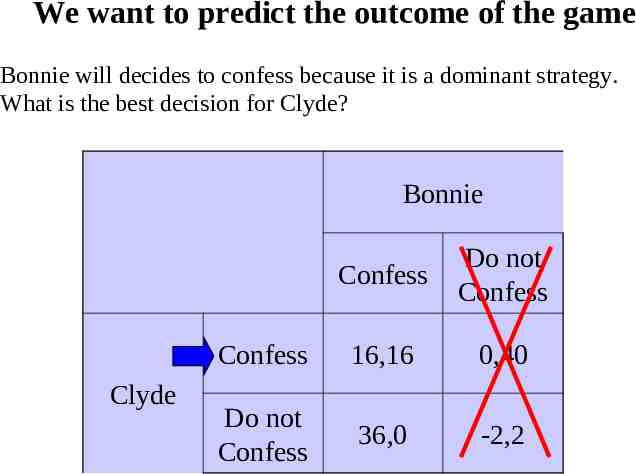
Dominated and Dominant Strategy In this case there is no dominant strategy for Clyde. But, for Bonnie confess is still a dominant strategy. Suppose that Clyde knows that Bonnie is rational and will choose to confess. Since Clyde knows that Bonnie will choose to confess, can we determine the outcome of the game?

We want to predict the outcome of the game Bonnie will decides to confess because it is a dominant strategy. What is the best decision for Clyde? Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 36,0 -2,2

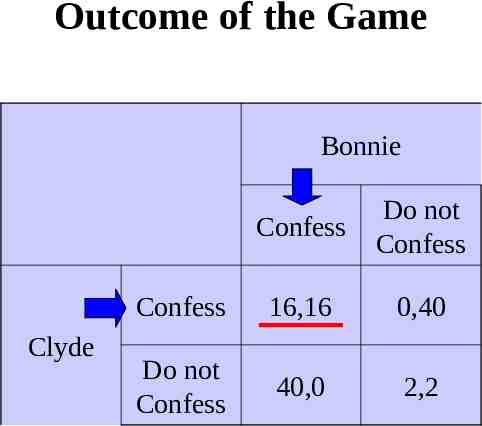
Outcome of the Game Bonnie Clyde Confess Do not Confess Confess 16,16 0,40 Do not Confess 40,0 2,2

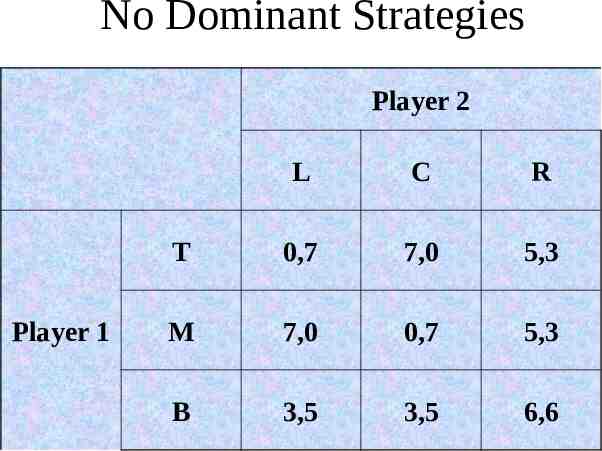
No Dominant Strategies In most games there are no dominant strategies for all players. We cannot use this method to predict the outcome of the game.

No Dominant Strategies Player 2 Player 1 L C R T 0,7 7,0 5,3 M 7,0 0,7 5,3 B 3,5 3,5 6,6

Nash Equilibrium The decisions of the players are a Nash Equilibrium if no individual prefers a different choice. In other words, each player is choosing the best strategy, given the strategies chosen by the other players.