Fuzzy Logic Control Lect 5 Fuzzy Logic Control Basil Hamed

Fuzzy Logic Control Lect 5 Fuzzy Logic Control Basil Hamed Electrical Engineering Islamic University of Gaza

Content Classical Control Fuzzy Logic Control The Architecture of Fuzzy Inference Systems Fuzzy Control Model – Mamdani Fuzzy models – Larsen Fuzzy Models – Sugeno Fuzzy Models – Tsukamoto Fuzzy models Examples Basil Hamed 2

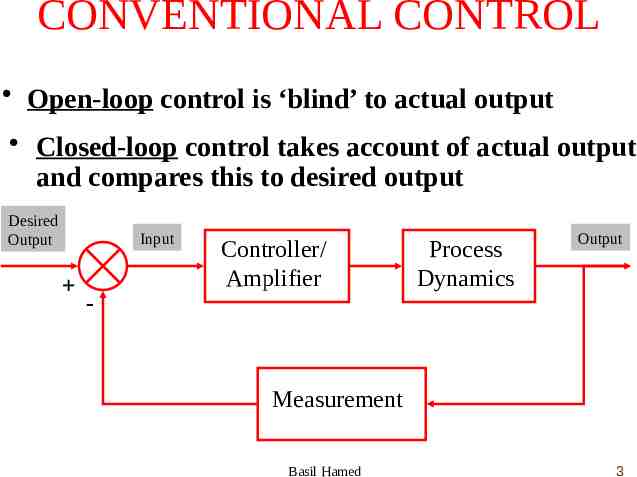
CONVENTIONAL CONTROL Open-loop control is ‘blind’ to actual output Closed-loop control takes account of actual output and compares this to desired output Desired Output Input - Controller/ Amplifier Process Dynamics Output Measurement Basil Hamed 3

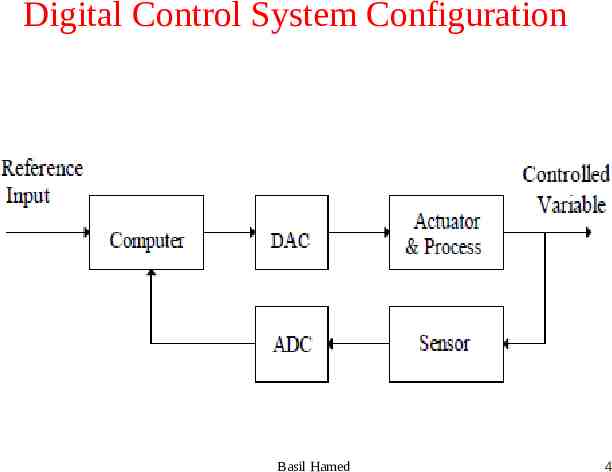
Digital Control System Configuration Basil Hamed 4

CONVENTIONAL CONTROL Example: design a cruise control system After gaining an intuitive understanding of the plant’s dynamics and establishing the design objectives, the control engineer typically solves the cruise control problem by doing the following: 1. Developing a model of the automobile dynamics (which may model vehicle and power train dynamics, tire and suspension dynamics, the effect of road grade variations, etc.). 2. Using the mathematical model, or a simplified version of it, to design a controller (e.g., via a linear model, develop a linear controller with techniques from classical control). Basil Hamed 5

CONVENTIONAL CONTROL 3. Using the mathematical model of the closed-loop system and mathematical or simulation-based analysis to study its performance (possibly leading to redesign). 4. Implementing the controller via, for example, a microprocessor, and evaluating the performance of the closed-loop system (again, possibly leading to redesign). Basil Hamed 6

CONVENTIONAL CONTROL Mathematical model of the plant: – never perfect – an abstraction of the real system – “is accurate enough to be able to design a controller that will work.”! – based on a system of differential equations Basil Hamed 7

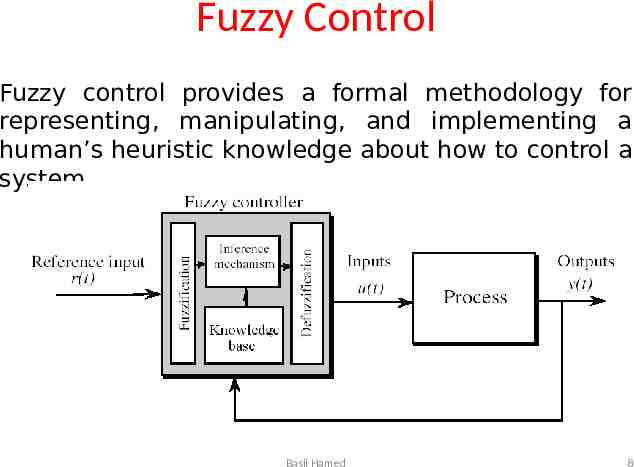
Fuzzy Control Fuzzy control provides a formal methodology for representing, manipulating, and implementing a human’s heuristic knowledge about how to control a system. Basil Hamed 8

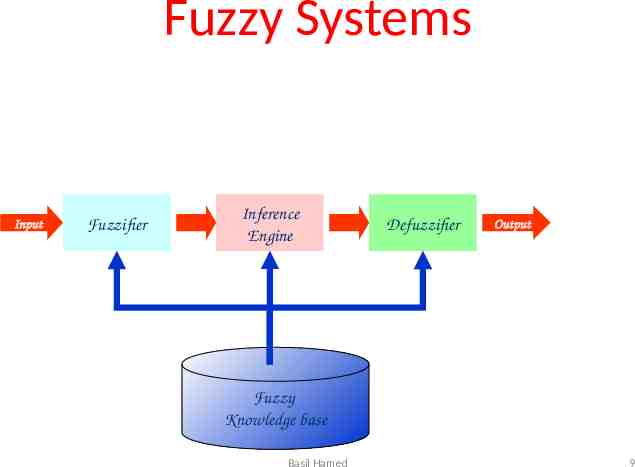
Fuzzy Systems Input Fuzzifier Inference Engine Defuzzifier Output Fuzzy Knowledge base Basil Hamed 9

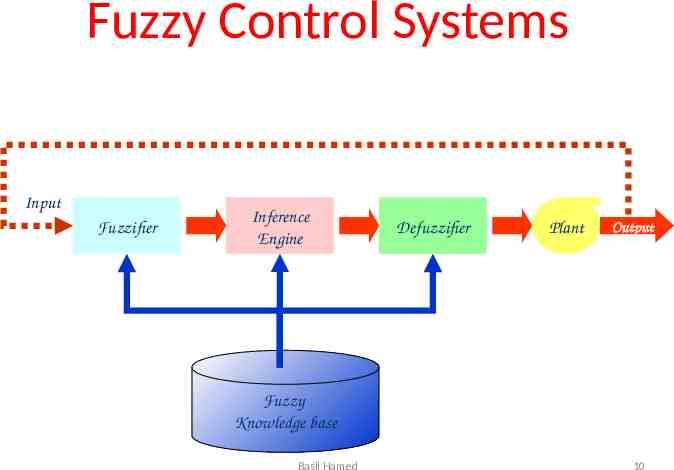
Fuzzy Control Systems Input Fuzzifier Inference Engine Defuzzifier Plant Output Fuzzy Knowledge base Basil Hamed 10

Fuzzy Logic Control Fuzzy controller design consist of turning intuitions, and any other information about how to control a system, into set of rules. These rules can then be applied to the system. If the rules adequately control the system, the design work is done. If the rules are inadequate, the way they fail provides information to change the rules. Basil Hamed 11

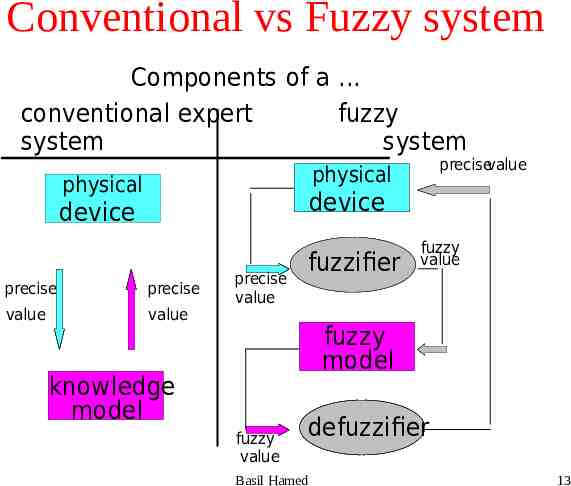
Components of Fuzzy system The components of a conventional expert system and a fuzzy system are the same. Fuzzy systems though contain fuzzifiers’. – Fuzzifiers convert crisp numbers into fuzzy numbers, Fuzzy systems contain defuzzifiers', – Defuzzifiers convert fuzzy numbers into crisp numbers. Basil Hamed 12

Conventional vs Fuzzy system Components of a . conventional expert fuzzy system system precisevalue physical physical device device precise precise value value precise value fuzzifier fuzzy value fuzzy model knowledge model fuzzy value defuzzifier Basil Hamed 13

In order to process the input to get the output reasoning there are six steps involved in the creation of a rule based fuzzy system: 1. Identify the inputs and their ranges and name them. 2. Identify the outputs and their ranges and name them. 3. Create the degree of fuzzy membership function for each input and output. 4. Construct the rule base that the system will operate under 5. Decide how the action will be executed by assigning strengths to the rules 6. Combine the rules and defuzzify the output Basil Hamed 14

Fuzzy Logic Control Type of Fuzzy Controllers: Mamdani Larsen TSK (Takagi Sugeno Kang) Tsukamoto Other methods Basil Hamed 15

Fuzzy Control Systems Mamdani Fuzzy models

Mamdani Fuzzy models The most commonly used fuzzy inference technique is the so-called Mamdani method. In 1975, Professor Ebrahim Mamdani of London University built one of the first fuzzy systems to control a steam engine and boiler combination. Original Goal: Control a steam engine & boiler combination by a set of linguistic control rules obtained from experienced human operators. Basil Hamed 17

Mamdani fuzzy inference The Mamdani-style fuzzy inference process is performed in four steps: 1. Fuzzification of the input variables, 2. Rule evaluation; 3. Aaggregation of the rule outputs, and finally 4. Defuzzification. Basil Hamed 18

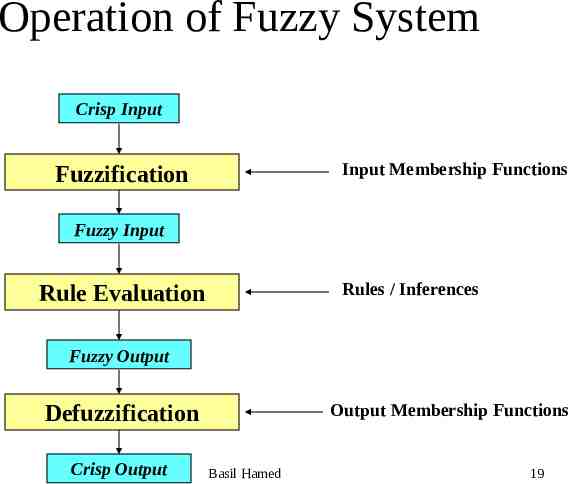
Operation of Fuzzy System Crisp Input Input Membership Functions Fuzzification Fuzzy Input Rules / Inferences Rule Evaluation Fuzzy Output Output Membership Functions Defuzzification Crisp Output Basil Hamed 19

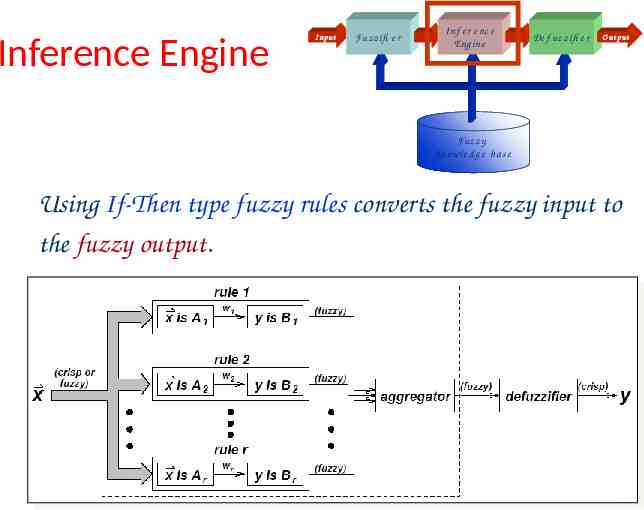
Inference Engine I nput Fuzzifi e r I nf e r e nc e Eng ine De f uzzifi e r O ut p ut Fuzzy Kno wle d g e b as e Using If-Then type fuzzy rules converts the fuzzy input to the fuzzy output. Basil Hamed 20

We examine a simple two-input one-output problem that includes three rules: Rule: 1 Rule: 1 IF x is A3 IF project funding is adequate OR y is B1 OR project staffing is small THEN z is C1 THEN risk is low Rule: 2 IF x is A2 AND y is B2 THEN z is C2 Rule: 2 IF project funding is marginal AND project staffing is large THEN risk is normal Rule: 3 IF x is A1 THEN z is C3 Rule: 3 IF project funding is inadequate THEN risk is high

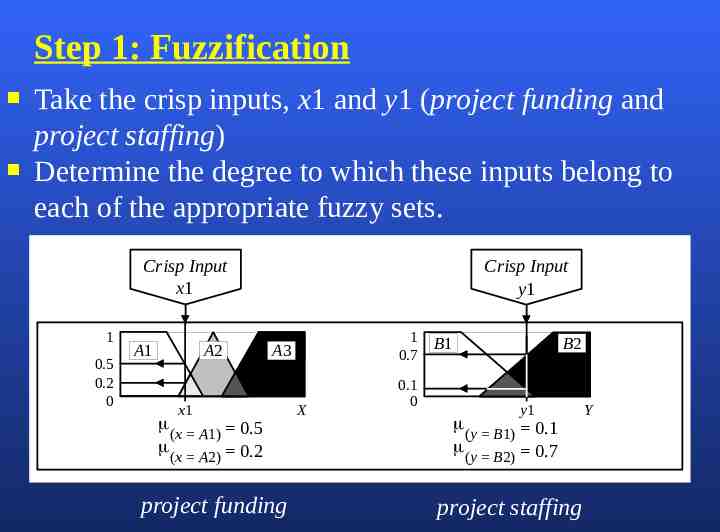
Step 1: Fuzzification Take the crisp inputs, x1 and y1 (project funding and project staffing) Determine the degree to which these inputs belong to each of the appropriate fuzzy sets. Crisp Input x1 1 0.5 0.2 0 A1 A2 Crisp Input y1 1 0.7 A3 x1 (x A1) 0.5 0.2 (x A2) project funding X B1 B2 0.1 0 y1 (y B1) 0.1 0.7 (y B2) project staffing Y

Step 2: Rule Evaluation take the fuzzified inputs, (x A1) 0.5, (x A2) 0.2, (y B1) 0.1 and (y B2) 0.7 apply them to the antecedents of the fuzzy rules. If a given fuzzy rule has multiple antecedents, the fuzzy operator (AND or OR) is used to obtain a single number that represents the result of the antecedent evaluation. This number (the truth value) is then applied to the consequent membership function. Basil Hamed 23

Step 2: Rule Evaluation To evaluate the disjunction of the rule antecedents, we use the OR fuzzy operation. Typically, fuzzy expert systems make use of the classical fuzzy operation union: A B(x) max [ A(x), B(x)] Similarly, in order to evaluate the conjunction of the rule antecedents, we apply the AND fuzzy operation intersection: A B(x) min [ A(x), B(x)] Basil Hamed 24

Mamdani-style rule evaluation 1 1 A3 1 B1 0.1 0.0 0 x1 0 X Rule 1: IF x is A3 (0.0) OR 1 y1 y is B1 (0.1) 1 A2 0 x1 y1 Rule 2: IF x is A2 (0.2) AND y is B2 (0.7) 1 0 A1 x1 Rule 3: IF x is A1 (0.5) Z z is C1 (0.1) AND (min) Y 0.2 C1 C2 THEN C3 0 THEN Z z is C2 (0.2) C2 0 X C3 0 1 0.5 C1 0.5 C2 1 B2 0 0.1 THEN 0.7 0.2 X Y OR (max) C1 C3 Z z is C3 (0.5)

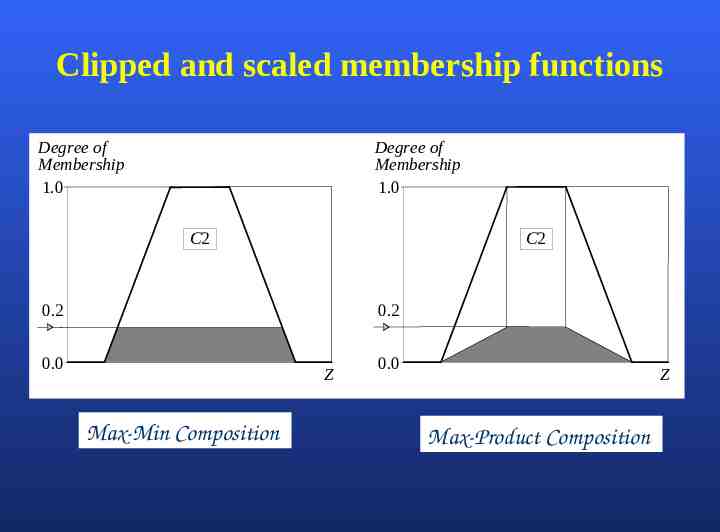
Now the result of the antecedent evaluation can be applied to the membership function of the consequent. There are two main methods for doing so: Clipping Scaling The most common method is to cut the consequent membership function at the level of the antecedent truth. Basil Hamed 26

This method is called clipping (Max-Min Composition) . The clipped fuzzy set loses some information. Clipping is still often preferred because: it involves less complex and faster mathematics it generates an aggregated output surface that is easier to defuzzify. Basil Hamed 27

While clipping is a frequently used method, scaling (Max-Product Composition) offers a better approach for preserving the original shape of the fuzzy set. The original membership function of the rule consequent is adjusted by multiplying all its membership degrees by the truth value of the rule antecedent. This method, which generally loses less information, can be very useful in fuzzy expert systems. Basil Hamed 28

Clipped and scaled membership functions Degree of Membership 1.0 Degree of Membership 1.0 C2 C2 0.2 0.2 0.0 Z Max-Min Composition 0.0 Z Max-Product Composition

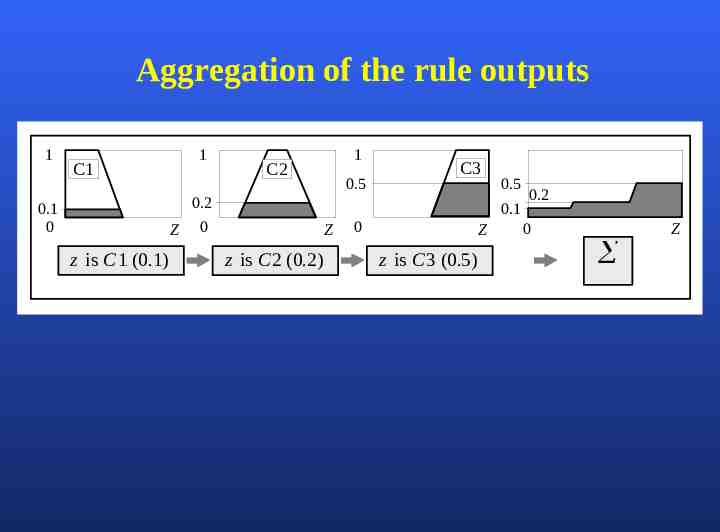
Step 3: Aggregation of The Rule Outputs Aggregation is the process of unification of the outputs of all rules. We take the membership functions of all rule consequents previously clipped or scaled and combine them into a single fuzzy set. Basil Hamed 30

Aggregation of the rule outputs 1 1 C1 1 C2 0.5 C3 0.2 0.1 0 Z z is C 1 (0.1) 0.5 0.1 0 Z z is C 2 (0.2) 0 Z z is C 3 (0.5) 0.2 0 Z

Step 4: Defuzzification Fuzziness helps us to evaluate the rules, but the final output of a fuzzy system has to be a crisp number. The input for the defuzzification process is the aggregated output fuzzy set and the output is a single number. Basil Hamed 32

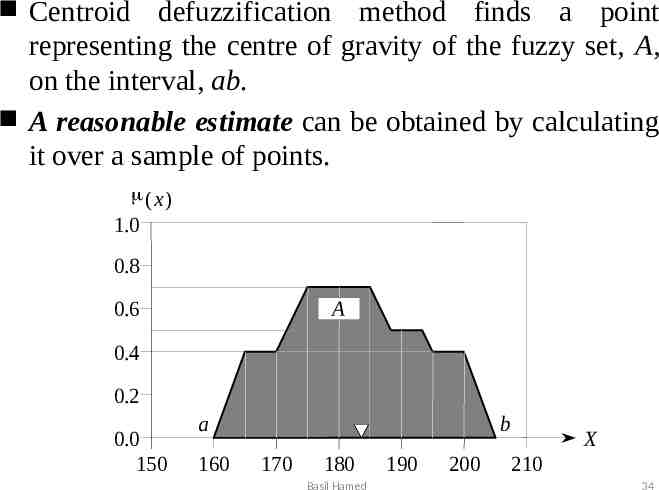
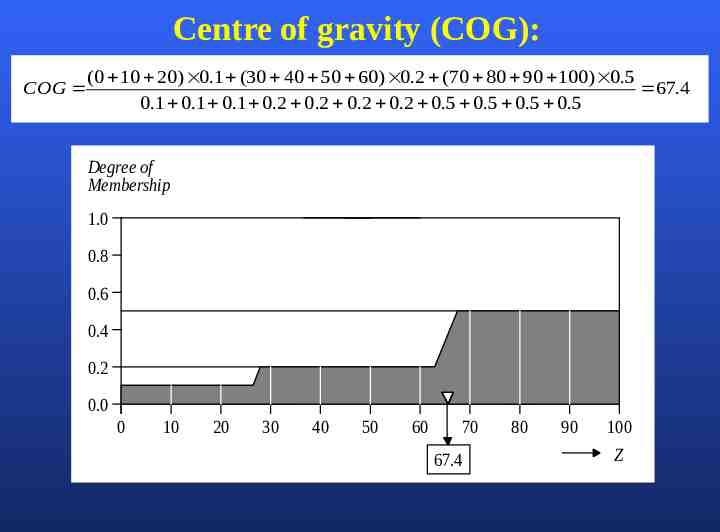
There are several defuzzification methods, but probably the most popular one is the centroid technique. It finds the point where a vertical line would slice the aggregate set into two equal masses. Mathematically this centre of gravity (COG) can be expressed as: b x x dx A COG ab x dx A a Basil Hamed 33

Centroid defuzzification method finds a point representing the centre of gravity of the fuzzy set, A, on the interval, ab. A reasonable estimate can be obtained by calculating it over a sample of points. (x) 1.0 0.8 A 0.6 0.4 0.2 0.0 150 a 160 b 170 180 Basil Hamed 190 200 X 210 34

Centre of gravity (COG): COG (0 10 20) 0.1 (30 40 50 60) 0.2 (70 80 90 100) 0.5 67.4 0.1 0.1 0.1 0.2 0.2 0.2 0.2 0.5 0.5 0.5 0.5 Degree of Membership 1.0 0.8 0.6 0.4 0.2 0.0 0 10 20 30 40 50 60 70 67.4 80 90 100 Z

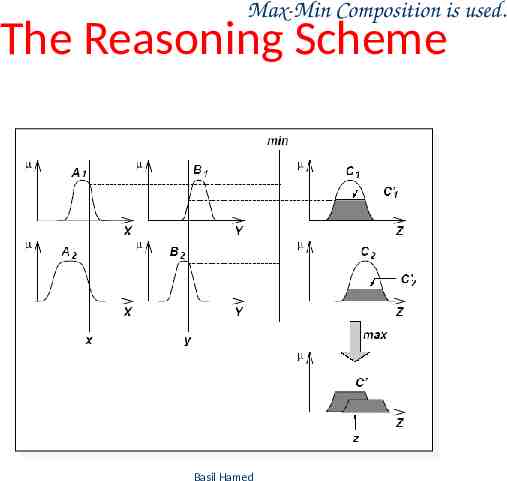
Max-Min Composition is used. The Reasoning Scheme Basil Hamed 36

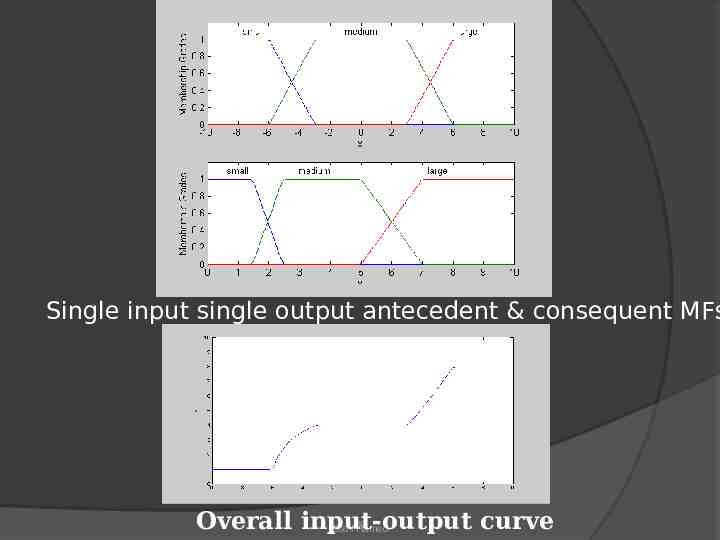
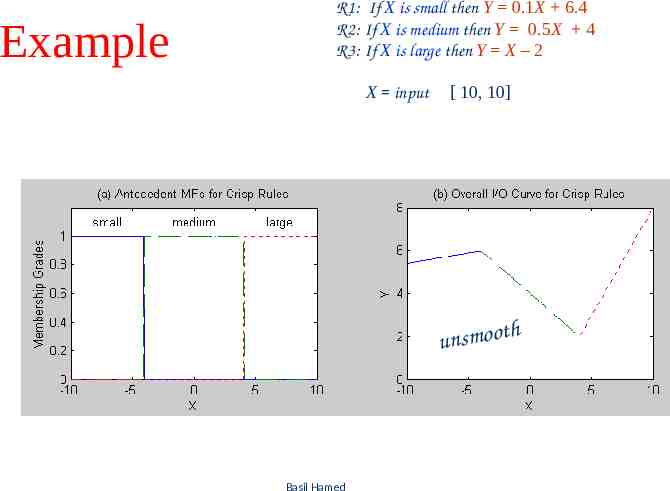
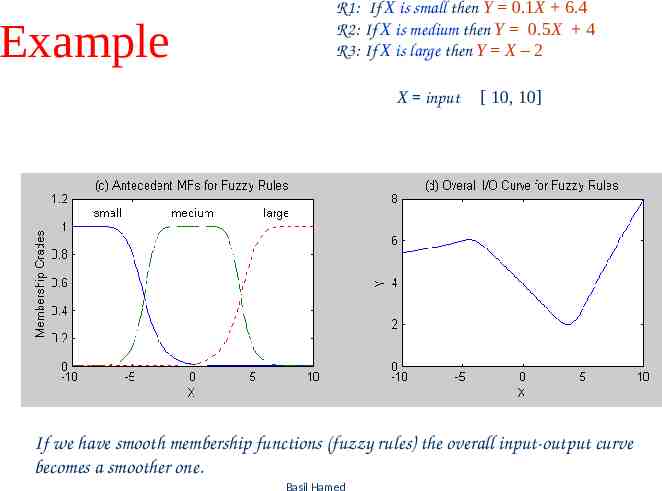
Examples for Mamdani Fuzzy Models Example #1 Single input single output Mamdani fuzzy model with 3 rules: If X is small then Y is small R1 If X is medium then Y is medium R2 Is X is large then Y is large R3 X input [-10, 10] Y output [0,10] Using centroid defuzzification, we obtain the following overall input-output curve Basil 37 Hamed

Single input single output antecedent & consequent MFs Overall input-output curve Basil 38 Hamed

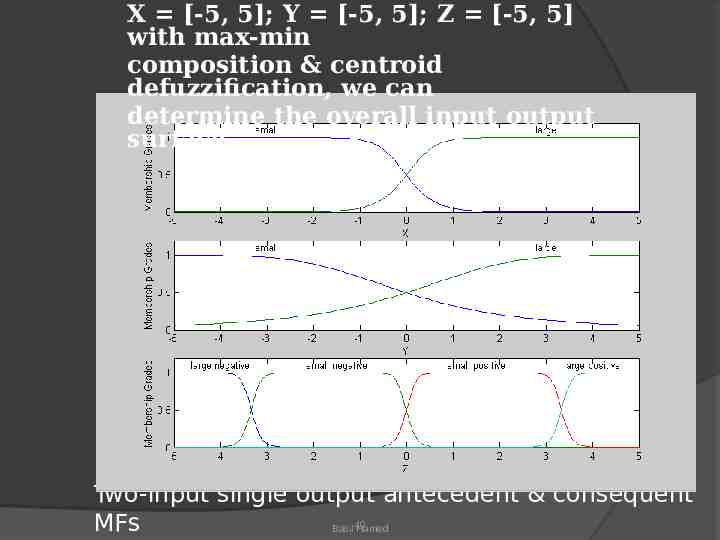
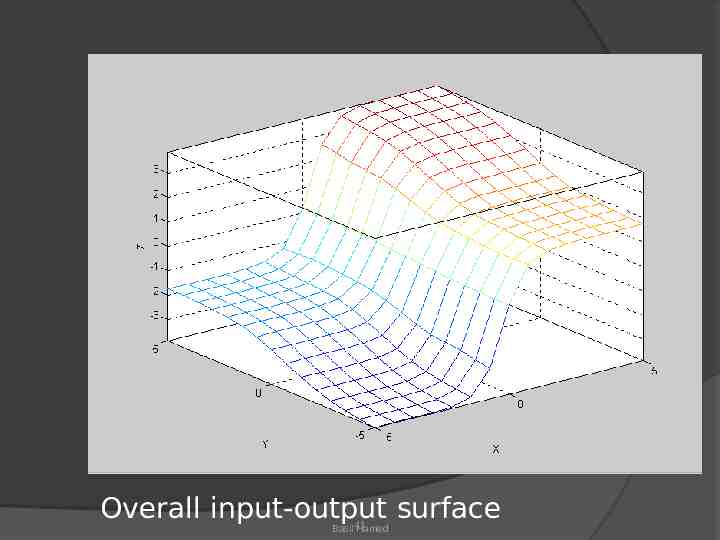
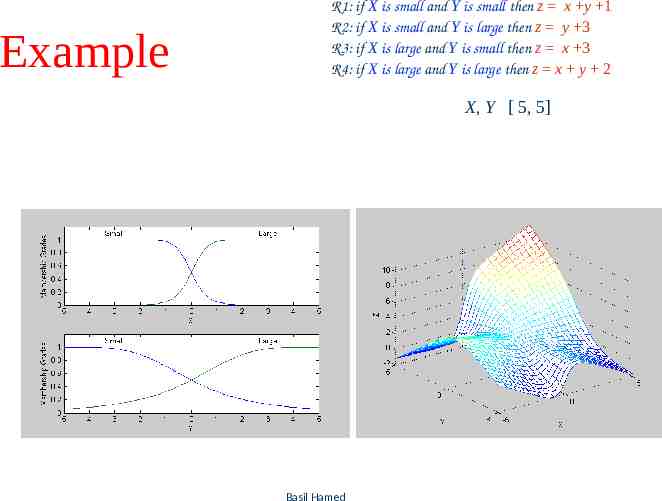
Example #2 (Mamdani Fuzzy models ) Two input single-output Mamdani fuzzy model with 4 rules: If X is small & Y is small then Z is negative large If X is small & Y is large then Z is negative small If X is large & Y is small then Z is positive small If X is large & Y is large then Z is positive large Basil 39 Hamed

X [-5, 5]; Y [-5, 5]; Z [-5, 5] with max-min composition & centroid defuzzification, we can determine the overall input output surface Two-input single output antecedent & consequent MFs Basil 40 Hamed

Overall input-output surface Basil 41 Hamed

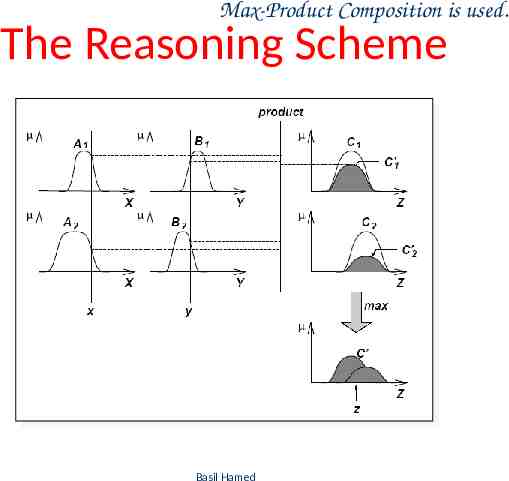
Larsen Fuzzy models Inference method: Larsen – product operator( ) for a fuzzy implication – max-product operator for the composition Basil Hamed 42

Max-Product Composition is used. The Reasoning Scheme Basil Hamed 43

Fuzzy Control Systems Sugeno Fuzzy Models

Sugeno Fuzzy Models Also known as TSK fuzzy model – Takagi, Sugeno & Kang, 1985 Goal: Generation of fuzzy rules from a given inputoutput data set. Basil Hamed 45

Sugeno Fuzzy Control Mamdani-style inference, requires to find the centroid of a two-dimensional shape by integrating across a continuously varying function. In general, this process is not computationally efficient. Michio Sugeno suggested to use a single spike, a singleton, as the membership function of the rule consequent. A fuzzy singleton, is a fuzzy set with a membership function that is unity at a single particular point on the universe of discourse and zero everywhere else. Basil Hamed 46

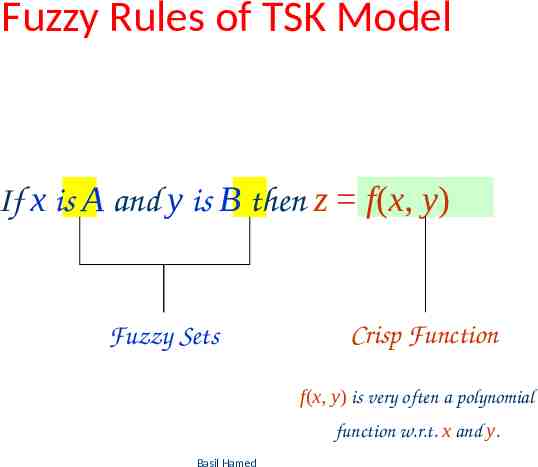
Sugeno-style fuzzy inference is very similar to the Mamdani method. Sugeno changed only a rule consequent. Instead of a fuzzy set, he used a mathematical function of the input variable. The format of the Sugeno-style fuzzy rule is IF x is A AND y is B THEN z is f (x, y) where x, y and z are linguistic variables A and B are fuzzy sets on universe of discourses X and Y f (x, y) is a mathematical function Basil Hamed 47

The most commonly used zero-order Sugeno fuzzy model applies fuzzy rules in the following form: IF x is A AND y is B THEN z is k where k is a constant. In this case, the output of each fuzzy rule is constant. All consequent membership functions are represented by singleton spikes. Basil Hamed 48

Fuzzy Rules of TSK Model If x is A and y is B then z f(x, y) Fuzzy Sets Crisp Function f(x, y) is very often a polynomial function w.r.t. x and y. Basil Hamed 49

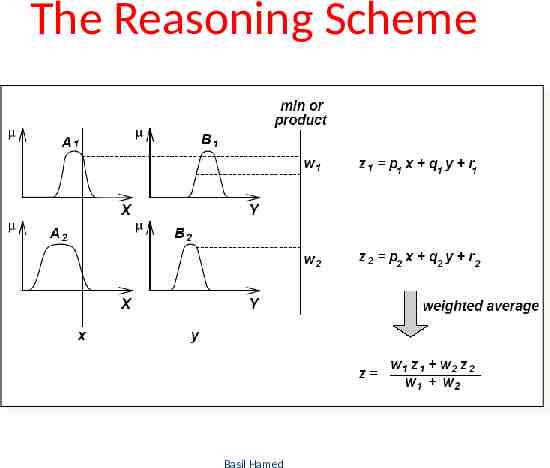
Examples R1: if X is small and Y is small then z x y 1 R2: if X is small and Y is large then z y 3 R3: if X is large and Y is small then z x 3 R4: if X is large and Y is large then z x y 2 Basil Hamed 50

The Reasoning Scheme Basil Hamed 51

Sugeno-style rule evaluation 1 1 A3 1 B1 0.1 0.0 0 x1 0 X Rule 1: IF x is A3 (0.0) y1 Y OR y is B1 (0.1) 1 1 A2 0 x1 y1 Rule 2: IF x is A2 (0.2) AND y is B2 (0.7) 1 0 A1 Z z is k1 (0.1) AND (min) Y 0.2 0 THEN k2 Z z is k2 (0.2) 0 X Rule 3: IF x is A1 (0.5) k1 1 0.5 0.5 x1 0 1 B2 0 0.1 THEN 0.7 0.2 X OR (max) THEN k3 z is k3 (0.5) Z

Sugeno-style aggregation of the rule outputs 1 0.1 0 1 1 1 0.5 0.5 0 0.1 0 0.2 k1 Z z is k1 (0.1) 0 k2 Z z is k2 (0.2) k3 Z z is k3 (0.5) 0.2 k1 k2 k3 Z

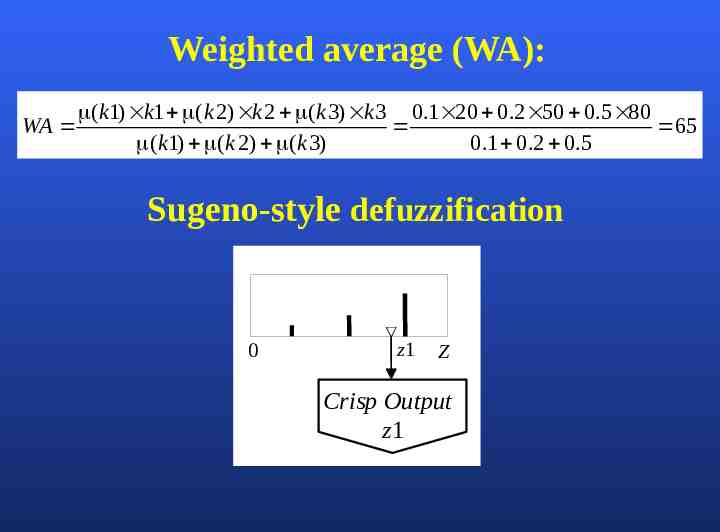
Weighted average (WA): (k1) k1 (k 2) k 2 (k 3) k 3 0.1 20 0.2 50 0.5 80 WA 65 (k1) (k 2) (k 3) 0.1 0.2 0.5 Sugeno-style defuzzification 0 z1 Z Crisp Output z1

Example R1: If X is small then Y 0.1X 6.4 R2: If X is medium then Y 0.5X 4 R3: If X is large then Y X – 2 X input [ 10, 10] h unsmoot Basil Hamed 55

Example R1: If X is small then Y 0.1X 6.4 R2: If X is medium then Y 0.5X 4 R3: If X is large then Y X – 2 X input [ 10, 10] If we have smooth membership functions (fuzzy rules) the overall input-output curve becomes a smoother one. Basil Hamed 56

Example R1: if X is small and Y is small then z x y 1 R2: if X is small and Y is large then z y 3 R3: if X is large and Y is small then z x 3 R4: if X is large and Y is large then z x y 2 X, Y [ 5, 5] Basil Hamed 57

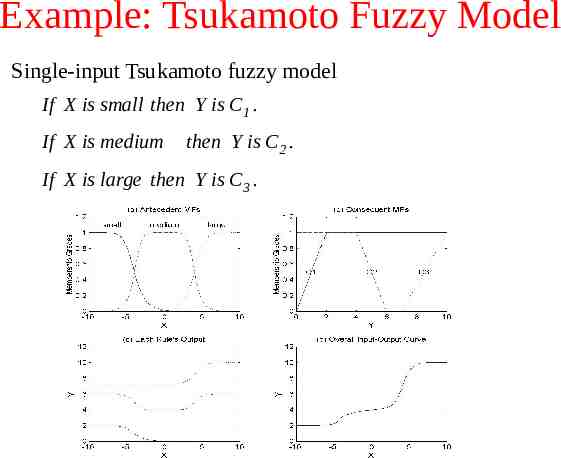
Tsukamoto Fuzzy Model The consequent of each fuzzy if-then rule: a fuzzy set with a monotonical MF. Overall output: the weighted average of each rule’s output. No defuzzification. Not as transparent as mamdani’s or Sugeno’s fuzzy model. Not follow strictly the compositional rule of inference: the output is always crisp.

Example: Tsukamoto Fuzzy Model Single-input Tsukamoto fuzzy model If X is small then Y is C1 . If X is medium then Y is C2 . If X is large then Y is C3 .

Basil Hamed 60 Different styles for Mamdani Fuzzy Models Larsen Fuzzy Models Sugeno Fuzzy Models Tsukamoto Fuzzy models The same style for Mamdani Fuzzy Models Larsen Fuzzy Models Sugeno Fuzzy Models Tsukamoto Fuzzy Models If antecedence then consequence . Review Fuzzy Models

How to make a decision on which method to apply Mamdani or Sugeno? Basil Hamed 61

Comparisons between Mamdani and Sugeno type Advantages of the Mamdani Method It is intuitive. It has widespread acceptance. It is well suited to human input. Advantages of the Sugeno Method It is computationally efficient. It works well with linear techniques (e.g., PID control). It works well with optimization and adaptive techniques. It has guaranteed continuity of the output surface. It is well suited to mathematical analysis. Basil Hamed 62

Tuning Fuzzy Systems 1. Review model input and output variables, and if required redefine their ranges. 2. Review the fuzzy sets, and if required define additional sets on the universe of discourse. The use of wide fuzzy sets may cause the fuzzy system to perform roughly. 3. Provide sufficient overlap between neighbouring sets. It is suggested that triangle-to-triangle and trapezoid-totriangle fuzzy sets should overlap between 25% to 50% of their bases. Basil Hamed 63

4. Review the existing rules, and if required add new rules to the rule base. 5. Adjust the rule execution weights. Most fuzzy logic tools allow control of the importance of rules by changing a weight multiplier. 6. Revise shapes of the fuzzy sets. In most cases, fuzzy systems are highly tolerant of a shape approximation. Basil Hamed 64

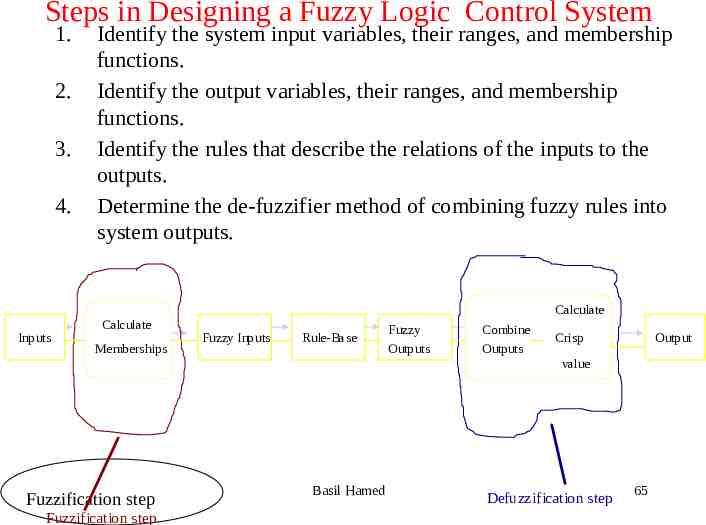
Steps in Designing a Fuzzy Logic Control System 1. 2. 3. 4. Identify the system input variables, their ranges, and membership functions. Identify the output variables, their ranges, and membership functions. Identify the rules that describe the relations of the inputs to the outputs. Determine the de-fuzzifier method of combining fuzzy rules into system outputs. Calculate Inputs Calculate Memberships Fuzzy Inputs Rule-Base Fuzzy Outputs Combine Outputs Crisp Output value Fuzzification step Fuzzification step Basil Hamed Defuzzification step 65

EXAMPLES

Building a Fuzzy Expert System: Case Study A service centre keeps spare parts and repairs failed ones. A customer brings a failed item and receives a spare of the same type. Failed parts are repaired, placed on the shelf, and thus become spares. The objective here is to advise a manager of the service centre on certain decision policies to keep the customers satisfied. Basil Hamed 67

Process of Developing a Fuzzy Expert System 1. Specify the problem and define linguistic variables. 2. Determine fuzzy sets. 3. Elicit and construct fuzzy rules. 4. Encode the fuzzy sets, fuzzy rules and procedures to perform fuzzy inference into the expert system. 5. Evaluate and tune the system. Basil Hamed 68

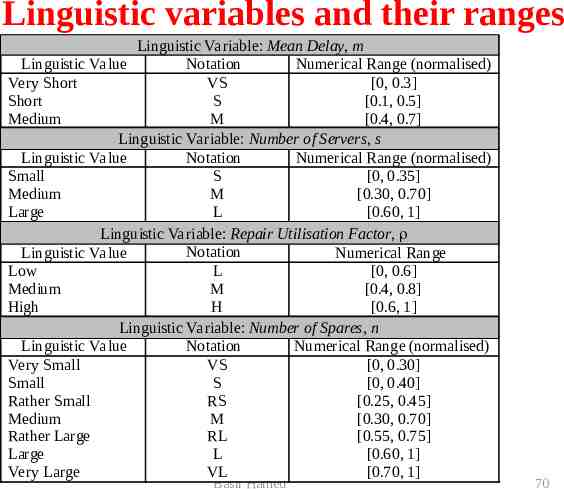
Step 1: Specify the problem and define linguistic variables There are four main linguistic variables: average waiting time (mean delay) m, repair utilisation factor of the service centre (is the ratio of the customer arrival day to the customer departure rate) number of servers s, and initial number of spare parts n . Basil Hamed 69

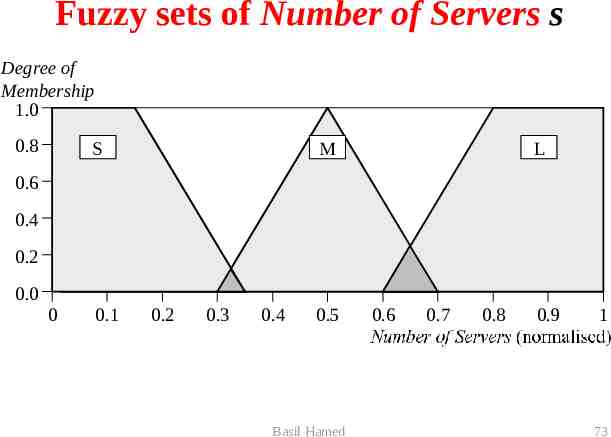
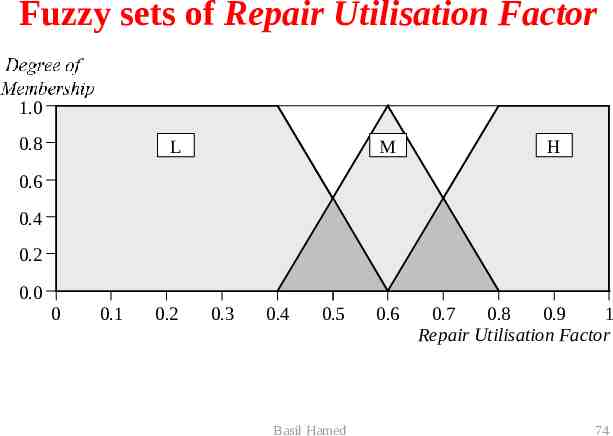
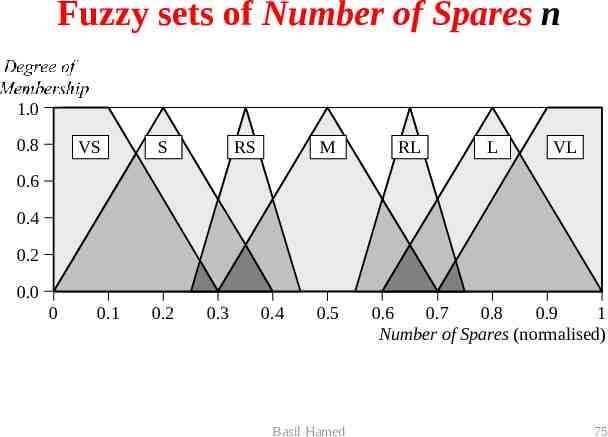
Linguistic variables and their ranges Linguistic Variable: Mean Delay, m Linguistic Va lue Notation Numerical Range (normalised) Very Short VS [0, 0.3] Short S [0.1, 0.5] Medium M [0.4, 0.7] Linguistic Variable: Number of Servers, s Linguistic Va lue Notation Numerical Range (normalised) Small S [0, 0.35] Medium M [0.30, 0.70] Large L [0.60, 1] Linguistic Variable: Repair Utilisation Factor, Notation Linguistic Va lue Numerical Range Low L [0, 0.6] Medium M [0.4, 0.8] High H [0.6, 1] Linguistic Va riable: Number of Spares, n Linguistic Va lue Notation Numerical Range (normalised) Very Small VS [0, 0.30] Small S [0, 0.40] Rather Small RS [0.25, 0.45] Medium M [0.30, 0.70] Rather Large RL [0.55, 0.75] Large L [0.60, 1] Very Large VL [0.70, 1] Basil Hamed 70

Step 2: Determine Fuzzy Sets Fuzzy sets can have a variety of shapes. However, a triangle or a trapezoid can often provide an adequate representation of the expert knowledge, and at the same time, significantly simplifies the process of computation. Basil Hamed 71

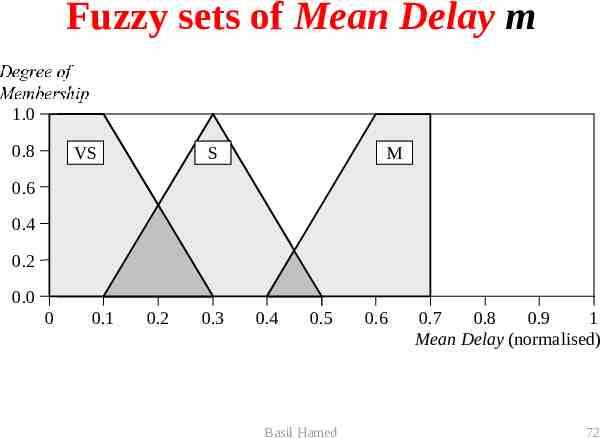
Fuzzy sets of Mean Delay m Degree of Membership 1.0 0.8 VS S M 0.6 0.4 0.2 0.0 0 0.1 0.2 0.3 0.4 0.5 Basil Hamed 0.6 0.7 0.8 0.9 1 Mean Delay (normalised) 72

Fuzzy sets of Number of Servers s Degree of Membership 1.0 0.8 S M L 0.6 0.4 0.2 0.0 0 0.1 0.2 0.3 0.4 0.5 Basil Hamed 0.6 0.7 0.8 0.9 1 73

Fuzzy sets of Repair Utilisation Factor Degree of Membership 1.0 0.8 L M H 0.6 0.4 0.2 0.0 0 0.1 0.2 0.3 0.4 0.5 Basil Hamed 0.6 0.7 0.8 0.9 1 Repair Utilisation Factor 74

Fuzzy sets of Number of Spares n Degree of Membership 1.0 0.8 VS S RS M RL L VL 0.6 0.4 0.2 0.0 0 0.1 0.2 0.3 0.4 0.5 Basil Hamed 0.6 0.7 0.8 0.9 1 Number of Spares (normalised) 75

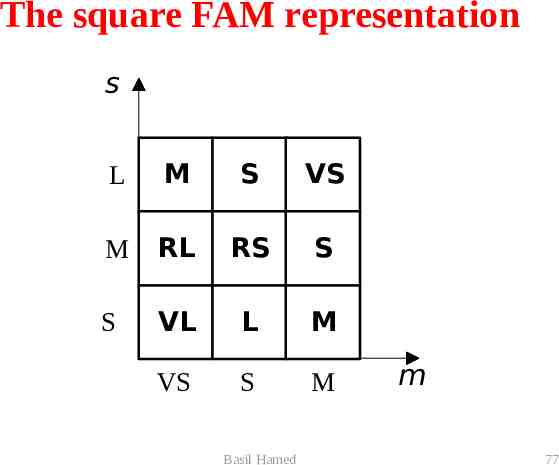
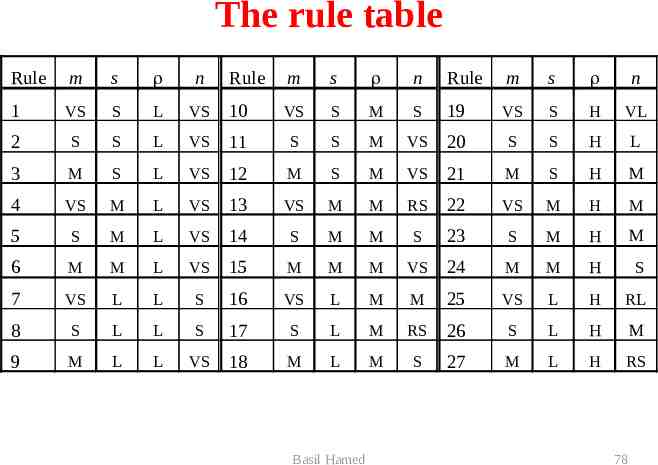
Step 3: Elicit and construct fuzzy rules To accomplish this task, we might ask the expert to describe how the problem can be solved using the fuzzy linguistic variables defined previously. Required knowledge also can be collected from other sources such as books, computer databases, flow diagrams and observed human behavior. The matrix form of representing fuzzy rules is called fuzzy associative memory (FAM). Basil Hamed 76

The square FAM representation s L M S VS M RL RS S S VL L M VS S M Basil Hamed m 77

The rule table Rule m s n Rule m s n Rule m s n 1 VS S L VS 10 VS S M S 19 VS S H VL 2 S S L VS 11 S S M VS 20 S S H L 3 M S L VS 12 M S M VS 21 M S H M 4 VS M L VS 13 VS M M RS 22 VS M H M 5 S M L VS 14 S M M S 23 S M H M 6 M M L VS 15 M M M VS 24 M M H S 7 VS L L S 16 VS L M M 25 VS L H RL 8 S L L S 17 S L M RS 26 S L H M 9 M L L VS 18 M L M S 27 M L H RS Basil Hamed 78

Rule Base 1 1. If (utilisation factor is L) then (number of spares is S) 2. If (utilisation factor is M) then (number of sparesis M) 3. If (utilisation factor is H) then (number of sparesis L) 4. If (mean delay is VS) and (number of serversis S) then (number of sparesis VL) 5. If (mean delay is S) and (number of serversis S) then (number of sparesis L) 6. If (mean delay is M) and (number of serversis S) then (number of sparesis M) 7. If (mean delay is VS) and (number of serversis M) then (number of sparesis RL) 8. If (mean delay is S) and (number of serversis M) then (number of sparesis RS) 9. If (mean delay is M) and (number of serversis M) then (number of spares is S) 10. If (mean delay is VS) and (number of servers is L) then (number of sparesis M) 11. If (mean delay is S) and (number of servers is L) then (number of sparesis S) 12. If (mean delay is M) and (number of servers is L) then (number of sparesis VS) Basil Hamed 79

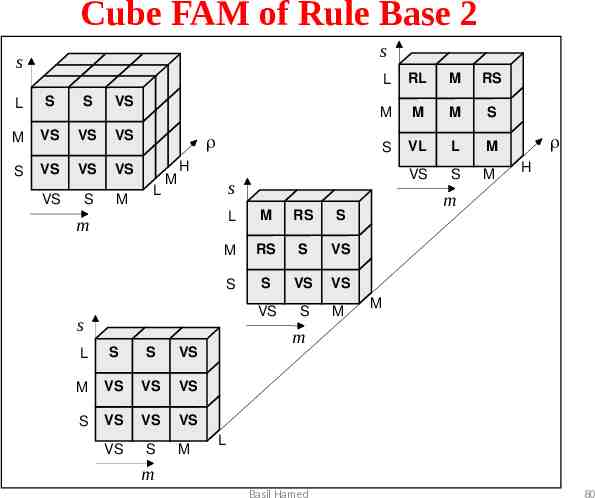
Cube FAM of Rule Base 2 s s L M S VS VS VS VS VS VS S S VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS H VS VS VS M L VS S M S VS M VS VS VS S VS VS VS VS S M M RS M M M S S VL L M VS S M s L M RS S M RS S VS S S VS VS VS S M s S RL m L L H m M m L m Basil Hamed 80

Step 4: Encode the fuzzy sets, fuzzy rules and procedures to perform fuzzy inference into the expert system To accomplish this task, we may choose one of two options: to build our system using a programming language such as C/C , Java, or to apply a fuzzy logic development tool such as MATLAB Fuzzy Logic Toolbox or Fuzzy Knowledge Builder. Basil Hamed 81

Step 5: Evaluate and Tune the System The last task is to evaluate and tune the system. We want to see whether our fuzzy system meets the requirements specified at the beginning. Several test situations depend on the mean delay, number of servers and repair utilisation factor. The Fuzzy Logic Toolbox can generate surface to help us analyse the system’s performance. Basil Hamed 82

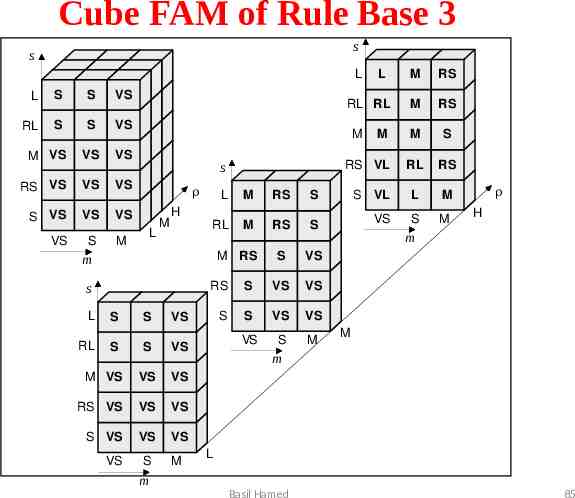
However, even now, the expert might not be satisfied with the system performance. To improve the system performance, we may use additional sets Rather Small and Rather Large on the universe of discourse Number of Servers, and then extend the rule base. Basil Hamed 83

Modified Fuzzy Sets of Number of Servers s Degree of Membership 1.0 0.8 S RS M RL L 0.6 0.4 0.2 0.0 0 0.1 0.2 0.3 0.4 0.5 Basil Hamed 0.6 0.7 0.8 0.9 1 Number of Servers (normalised) 84

Cube FAM of Rule Base 3 s s L RL M RS S VS VS VS VS VS VS S S VS VS VS VS VS VS VS S S VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS VS H VS VS VS M L VS S M L L RL S S s L M RS S RL M RS S S VS VS M VS VS VS RS VS VS VS S VS VS VS S M VS RS S VS VS S S VS VS VS S M VS S RS M RS M M S RS VL RL RS S VL L M VS S M M M RS S M RL RL m s L H m M m L m Basil Hamed 85

Fuzzy Control Example Basil Hamed 86

Input Fuzzy Sets Angle:- -30 to 30 degrees Basil Hamed 87

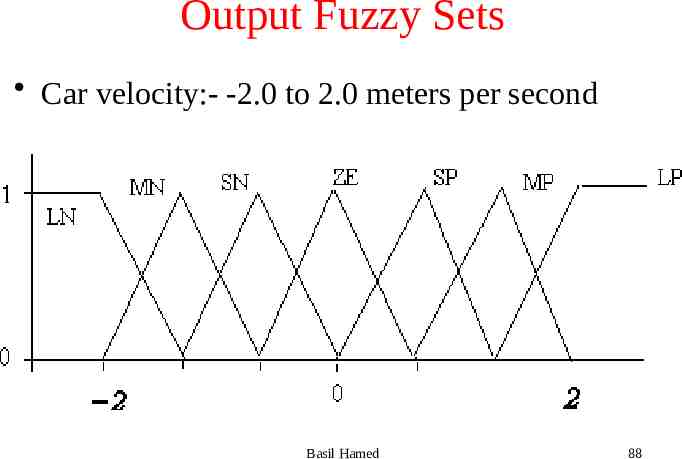
Output Fuzzy Sets Car velocity:- -2.0 to 2.0 meters per second Basil Hamed 88

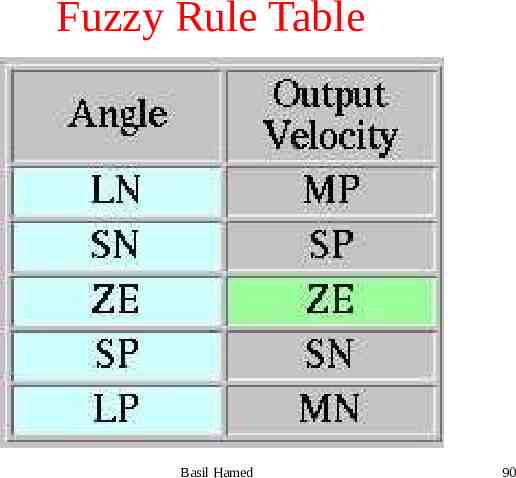
Fuzzy Rules If Angle is Zero then output ? If Angle is SP then output ? If Angle is SN then output ? If Angle is LP then output ? If Angle is LN then output ? Basil Hamed 89

Fuzzy Rule Table Basil Hamed 90

Extended System Make use of additional information – angular velocity:- -5.0 to 5.0 degrees/ second Gives better control Basil Hamed 91

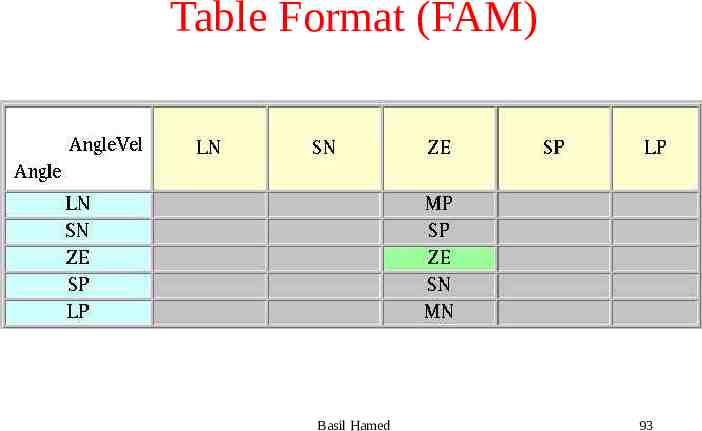
New Fuzzy Rules Make use of old Fuzzy rules for angular velocity Zero If Angle is Zero and Angular vel is Zero – then output Zero velocity If Angle is SP and Angular vel is Zero – then output SN velocity If Angle is SN and Angular vel is Zero – then output SP velocity Basil Hamed 92

Table Format (FAM) Basil Hamed 93

Complete Table When angular velocity is opposite to the angle do nothing – System can correct itself If Angle is SP and Angular velocity is SN – then output ZE velocity etc Basil Hamed 94

Example Inputs:10 degrees, -3.5 degrees/sec Fuzzified Values Inference Rules Output Fuzzy Sets Defuzzified Values Basil Hamed 95

HW 4 Design fuzzy control for the inverted pendulum problem using Matlab or LabView Due 10/11/2013 Basil Hamed 96