Frequency Response of Rational Systems Quote of the Day If

Frequency Response of Rational Systems Quote of the Day If knowledge can create problems, it is not through ignorance that we can solve them. Isaac Asimov Content and Figures are from Discrete-Time Signal Processing, 2e by Oppenheim, Shafer, and Buck, 1999-2000 Prentice Hall Inc.

Frequency Response of Rational System Functions DTFT of a stable and LTI rational system function M He j bk e M 1 c e j k k 0 N j k a e k b 0 a0 k 0 j k k 1 N 1 d e j k k 1 Magnitude Response M H ej b0 a0 j 1 c e k k 1 N j 1 d e k k 1 Magnitude Squared He j 2 M H e H e j j b0 a0 2 1 c e 1 c e * k k 1 N 1 k 1 Copyright (C) 2005 Güner Arslan j j k dk e j 1 d*k e j 351M Digital Signal Processing 2

Log Magnitude Response Log Magnitude in decibels (dB) 20 log10 H e j M b0 20 log10 20 log10 1 ck e j a0 k 1 N j 20 log 1 d e 10 k k 1 Gain in dB 20 log10 H e j Attenuation in dB - 20 log10 H e j Gain in dB Example: – H(ej ) 0.001 translates into –60dB gain or 60dB attenuation – H(ej ) 1 translates into 0dB gain – H(ej ) 0.5 translates into -6dB gain Output of system 20 log10 Y e j 20 log10 H e j 20 log10 X e j Copyright (C) 2005 Güner Arslan 351M Digital Signal Processing 3

Phase Response Phase response of a rational system function H e j b0 M 1 ck e j a0 k 1 N 1 d e j k k 1 Corresponding group delay grdH e j d arg 1 ck e j k 1 d M dd arg 1 d e N j k k 1 – Here arg[.] represents the continuous (unwrapped) phase – Work it out to get M dk 2 1 d grd H e j k 1 Copyright (C) 2005 Güner Arslan k Re dk e j 2 2 Re dk e j M k 1 ck 2 1 ck 351M Digital Signal Processing Re ck e j 2 2 Re ck e j 4

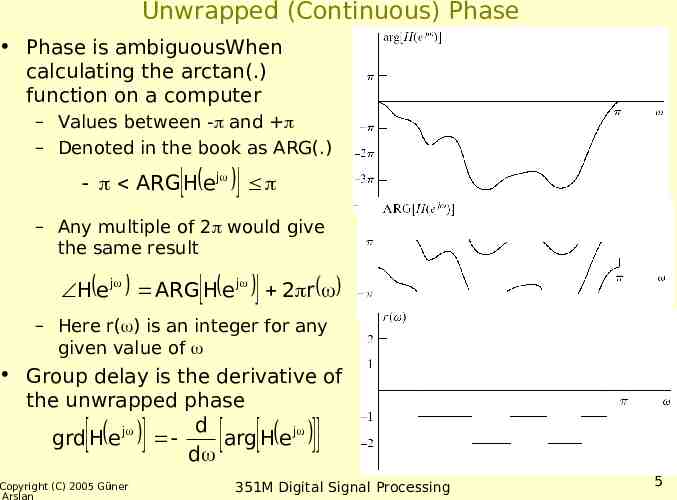
Unwrapped (Continuous) Phase Phase is ambiguousWhen calculating the arctan(.) function on a computer – Values between - and – Denoted in the book as ARG(.) ARG H e j – Any multiple of 2 would give the same result H e j ARG H e j 2 r – Here r( ) is an integer for any given value of Group delay is the derivative of the unwrapped phase d j grd H e arg H e j d Copyright (C) 2005 Güner Arslan 351M Digital Signal Processing 5

Frequency Response of a Single Zero or Pole Let’s analyze the effect of a single term 1 ck e j 2 j 1 re e j 2 1 r 2 2r cos If we represent it in dB 20 log10 1 re j e j 10 log10 1 r 2 2r cos The phase term is written as j ARG 1 re e j r sin arctan 1 r cos And the group delay obtained by differentiating the phase grd 1 re j e j r 2 r cos r 2 r cos 2 2 j j 1 r 2r cos 1 re e Maximum and minimum value of magnitude 1 r 2r cos 10 log 1 r 2r 20 log 10 log10 1 r 2 2r cos 10 log10 1 r 2 2r 20 log10 1 r 10 log10 2 2 10 10 1 r Demo at Mississippi State and at Arizona State University Copyright (C) 2005 Güner Arslan 351M Digital Signal Processing 6