Forecasting Dr. Everette S. Gardner, Jr.

Forecasting Dr. Everette S. Gardner, Jr.

Judgment exercises Exercise 1 Finished files are the result of years of scientific study combined with the experience of years. How many times does the letter F appear in the sentence above? Count them only once; do not go back and count them again. How confident are you in your answer? Rate your confidence on a scale of 0 to 100, where 0 means that you are sure you are wrong, and 100 means that you are sure you right. Forecasting 2

Judgment exercises (cont.) Exercise 2 Threatened by a superior enemy force, the general faces a dilemma. His intelligence officers say his soldiers will be caught in an ambush in which 600 of them will die unless he leads them to safety by one of two available routes. If he takes the first route, 200 soldiers will be saved. If he takes the second route, there’s a one-third chance that 600 soldiers will be saved and a two-thirds chance that none will be saved. Which route should he take? Forecasting 3

Judgment exercises (cont.) Exercise 3 The general again has to choose between two escape routes. But this time his aides tell him that if he takes the first, 400 soldiers will die. If he takes the second, there’s a one-third chance that no soldiers will die, and a twothirds chance that 600 soldiers will die. Which route should he take? Forecasting 4

Judgment exercises (cont.) Exercise 4 Linda is 31, single, outspoken, and very bright. She majored in philosophy in college. As a student, she was deeply concerned with discrimination and other social issues, and participated in anti-nuclear demonstrations. Which statement is more likely? a. Linda is a bank teller. b. Linda is a bank teller and active in the feminist movement. Forecasting 5

Human biases in forecasting Company Politics Forecast what the boss wants to hear Overconfidence Confidence has no relation to accuracy Wishful thinking Optimistic forecasts more probable Success/failure attribution Good forecasts due to skill, bad due to chance Forecasting 6

Human biases in forecasting Gambler’s fallacy Bad luck and good luck will balance out Data presentation Misleading graphs/tables easily accepted Conservatism Refusal to accept drastic change Forecasting 7

Forecasting methods Human judgment Subject to bias and inconsistency Models usually beat humans Time series forecasting Based on analysis of past history Cheap and easy On average, most accurate method Should always be attempted Forecasting 8

Forecasting methods (cont.) Regression modeling Based on causal relationships Expensive and difficult Must forecast independent variables Growth or market development models Based on assumed growth patterns Cheap and easy Difficult to validate Forecasting 9

Can your data be forecasted by a model? Use common sense Abrupt turning points usually impossible to predict Compare your accuracy to a naïve benchmark Forecast for next period is the same as the data this period If you cannot beat a naïve benchmark, forecasting is usually futile Forecasting 10

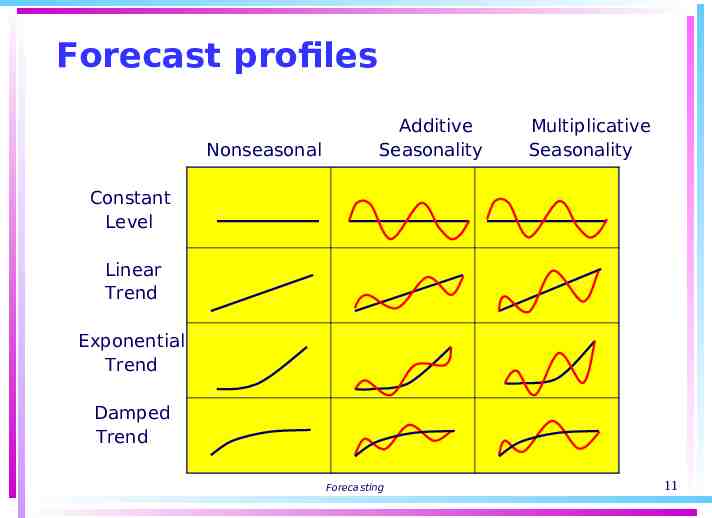
Forecast profiles Nonseasonal Additive Seasonality Multiplicative Seasonality Constant Level Linear Trend Exponential Trend Damped Trend Forecasting 11

Simple exponential smoothing (1) Error in t Actual data – Forecast for t (2) Forecast for t 1 Forecast for t α(Error in t) To get started: Set first forecast equal to mean of first few data. Smoothing weight (α): In practice, α is usually 0.30 – 0.50. Effects of extreme α values: If α 0, the forecast never changes. If α 1, this is a naïve or random walk model. Forecasting Simple.xls 12

Error measures for evaluating forecast models MAD Mean absolute deviation (error) MSE Mean squared error MAPE Mean absolute percentage error Forecasting 13

Smoothing a linear trend (1) Error in t Actual data - Forecast for t (2) Level at end of t Forecast for t h 1(Error in t) (3) Trend at end of t Trend at end of t–1 h 2(Error in t) (4) Forecast for t 1 Level at end of t Trend at end of t To get started, set: Initial trend Average growth in first four data Initial level First data observation – initial trend Search for weights in the following ranges: Level weight (h1) 0.10 to 0.90, increments of .10 Trend weight (h2) 0.05 to 0.30, increments of .05 Forecasting Trendsmooth.xls 14

The general trend model (1) Error in t Actual data – Forecast for t (2) Level at end of t Forecast for t h1(Error in t) (3) Trend at end of t ø(Trend at end of t – 1) h2(Error in t) (4) Forecast for t 1 Level at end of t ø(Trend at end of t) Long-term forecasting: Forecast for t 2 Forecast for t 1 ø2(Trend at end of t) Forecast for t 3 Forecast for t 2 ø3(Trend at end of t) Trend possibilities: If ø 1, the trend is damped. If ø 1, the trend is linear. If ø 1, the trend is exponential. If ø 0, there is no trend (same as simple smoothing). Forecasting 15

Starting up the general trend model Initial values Initial trend Average growth in first four data Initial level First data observation – Initial trend Search for parameters in the following ranges Level weight (h1) 0.10 to 0.90 Trend weight (h2) 0.05 to 0.30 Phi (ø) 0.60 to 1.00 Forecasting 16

Multiplicative seasonality The seasonal index is the expected ratio of actual data to the average for the year. Actual data / Index Seasonally adjusted data Seasonally adjusted data x Index Actual data Forecasting Multimon.xls 17

Multiplicative seasonal adjustment 1. Compute moving average based on length of seasonality (4 quarters or 12 months). 2. Divide actual data by corresponding moving average. 3. Average ratios to eliminate randomness. 4. Compute normalization factor to adjust mean ratios so they sum to 4 (quarterly data) or 12 (monthly data). 5. Multiply mean ratios by normalization factor to get final seasonal indexes. 6. Deseasonalize data by dividing by the seasonal index. 7. Forecast deseasonalized data. 8. Seasonalize forecasts from step 7 to get final forecasts. Forecasting 18

Additive seasonality The seasonal index is the expected difference between actual data and the average for the year. Actual data - Index Seasonally adjusted data Seasonally adjusted data Index Actual data Forecasting Additmon.xls 19

Additive seasonal adjustment 1. Compute moving average based on length of seasonality (4 quarters or 12 months). 2. Compute differences: Actual data - moving average. 3. Average differences to eliminate randomness. 4. Compute normalization factor to adjust mean differences so they sum to zero. 5. Compute final indexes: Mean difference – normalization factor. 6. Deseasonalize data: Actual data – seasonal index. 7. Forecast deseasonalized data. 8. Seasonalize forecasts from step 7 to get final forecasts. Forecasting 20

Forecasting simulations Dynamic simulation Short-range (one-step-ahead) forecasting test Use data in fit periods to select model During forecast periods: 1. Make one forecast. 2. Observe error. 3. Adjust model. 4. Go to 1. Static simulation Long-range forecasting test Use data in fit periods to select model Make all forecasts at once Forecasting 21

Data transformations for forecasting Deseasonalize Isolates trend % Change Isolates trend Natural log Converts exponential trend to linear Square root Reduce variance Aggregate Quarterly or monthly data to annual Forecasting 22

Forecasting management Organize for forecasting Pinpoint responsibility Only one corporate forecast Separate forecasting and planning Monitor accuracy Choose a standard measure Keep a track record Benchmark Hold performance reviews Scrub the data Adjust outliers Throw out unique data Forecasting 23

Forecasting management (cont.) Compare alternative forecasts Top-down vs. bottom up Monthly vs. quarterly data Deseasonalized vs. raw data Percent change data Time series forecasts Regression forecasts Simulate forecasting One-step-ahead Long-range Estimate confidence limits What is the range of forecast errors in past? Forecasting 24