FNCE 4070: FINANCIAL MARKETS AND INSTITUTIONS Lecture 5: The Term

FNCE 4070: FINANCIAL MARKETS AND INSTITUTIONS Lecture 5: The Term Structure of Interest Rates Yield Curves Spot and Forward Interest Rates The Pure Expectations Model of Yield Curves

Where is this Financial Center? Arab Spring Risk. Cairo stock market closed from January 27, 2011 to March 23, 2011

Relationship of Yields to Maturity In previous lectures we have discussed various factors which can account for differences in market interest rates: For example, inflation, risk of default, business cycles, flight to safety, and term to maturity. In this lecture we will expand on term to maturity as a factor and do so in the context of yield curves (called the “term structure of interest rates”).

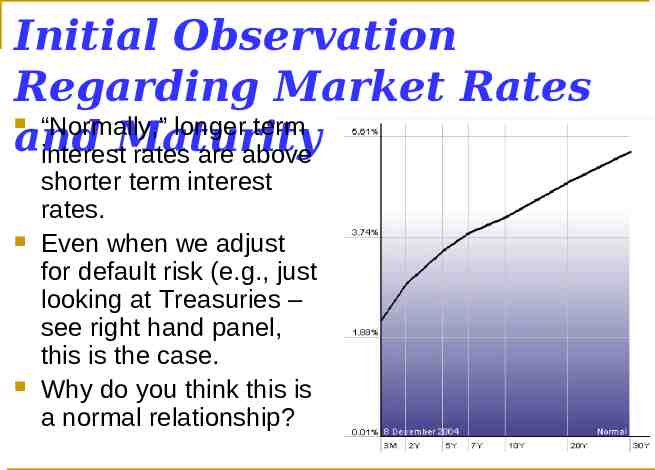
Initial Observation Regarding Market Rates “Normally,” longer term and interestMaturity rates are above shorter term interest rates. Even when we adjust for default risk (e.g., just looking at Treasuries – see right hand panel, this is the case. Why do you think this is a normal relationship?

Why Might we Assume that the Long Term Rate will be Above the Short Because of theTerm? risks associated with committing one’s capital for longer periods of time: Uncertainty about inflation. Uncertainty about economic activity. Knowledge of the price (i.e., interest rate) risk relationship regarding longer term issues. And if dealing with debt which is not free from default risk, uncertainty about future cash flows, risk of default and credit ratings.

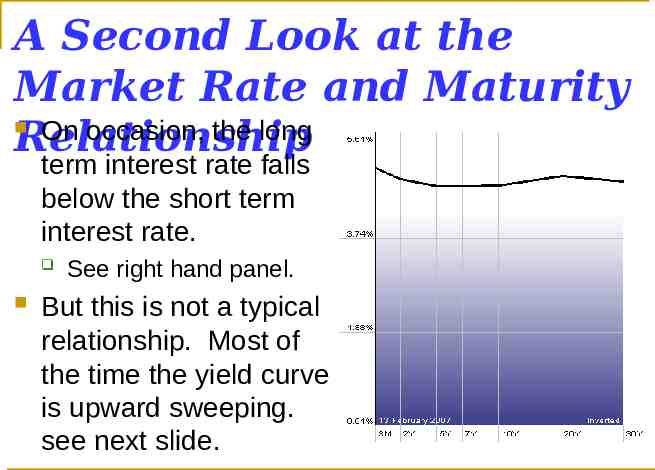
A Second Look at the Market Rate and Maturity On occasion, the long Relationship term interest rate falls below the short term interest rate. See right hand panel. But this is not a typical relationship. Most of the time the yield curve is upward sweeping. see next slide.

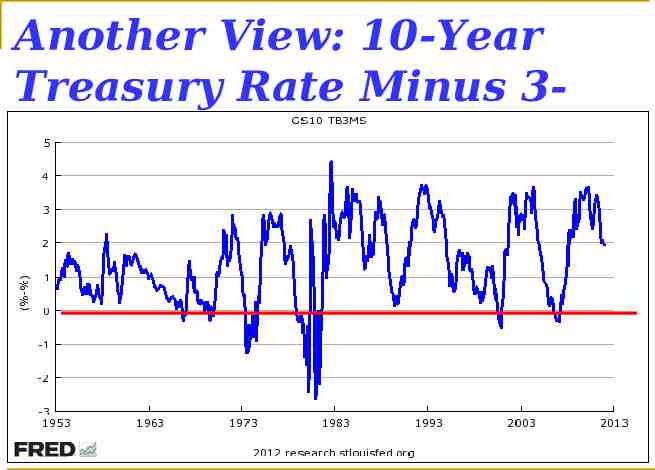
Another View: 10-Year Treasury Rate Minus 3Month Treasury Rate

How Can We Illustrate the Relationship Between Interest Rates Maturity? (1) Weand can look at interest rates over time. Compare movements (or differentials) of long term rates to short term rates over some historical period. OR (2) We can look at interest rates at a point in time, i.e., on a particular date. What is the short term interest rate, the intermediate term rate, and the long term interest rate on a specific date? This last approach is referred to as a yield curve.

Construction a Yield Curve A yield curve is simply a graphic presentation of the relationship of “term to maturity” and “yields to maturity” (interest rate) on a given date for seasoned issues. To construct it we plot: Term to maturity on the X axis, with its Corresponding interest rate on the Y axis, or: Interest Rate (yield to maturity) Term to maturity

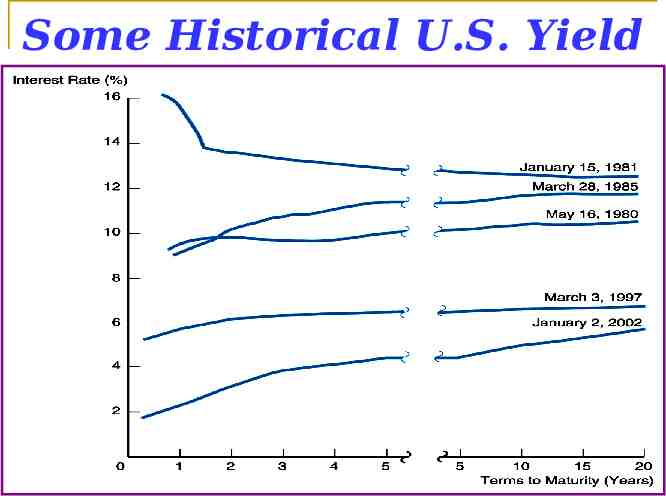
Summary: Three Yield Curve Shapes There are three basic shapes that yield curves can take. These are: Ascending Yield Curves (“Upward Sloping; Positive”) : Long term interest rates higher than short interest term Descending Yield Curves (“Downward Sloping; Inverted; Negative”) : Short term interest rates higher than long term interest rates. (Relatively) Flat Yield Curves: Long term and short term rates essentially the same. Next slide illustrates these three basic shapes for historical U.S. data.

Some Historical U.S. Yield Curves

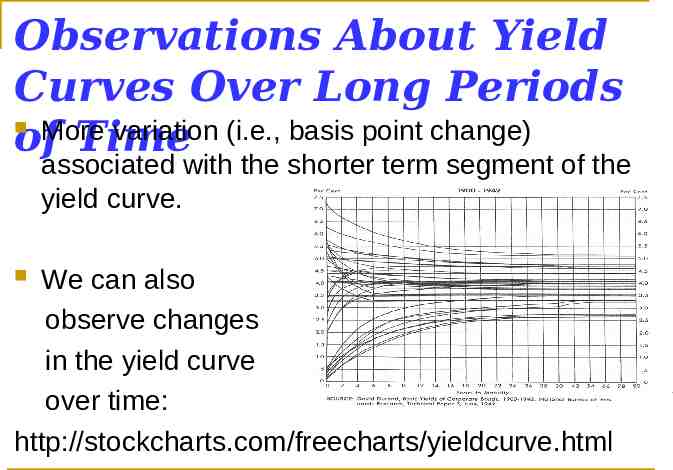
Observations About Yield Curves Over Long Periods More variation (i.e., basis point change) of Time associated with the shorter term segment of the yield curve. We can also observe changes in the yield curve over time: http://stockcharts.com/freecharts/yieldcurve.html

Theories to Explain the Yield There are three generally accepted theories or Curve explanations of the yield curve, these are: These theories are potentially important because they provide a framework for understanding the shape of the yield curve, but perhaps more importantly, we can use them to: (Pure) Expectations Theory Liquidity Premium Theory Market Segmentations Theory (1) Forecasting future interest rates. (2) Forecasting future changes in economic activity (i.e., business cycle turning points). (3) Forecasting future rates of inflation. In this lecture, we will concentrate on the first theory, the Pure Expectations Theory.

The (Pure) Expectations Financial market’s expectations regarding future interest rates will shape the observed yield curve. Theory Model assumes that financial markets are efficient. What does this mean for interest rates? Market participants are constantly forming expectations about future interest rates (these are referred to as forward interest rates). These forward rates are based upon the markets’ analysis of all relevant events likely to affect interest rates in the future (e.g., central bank actions, inflationary expectations, business cycles, etc.). These forward rates are incorporated into current market interest rates (also referred to as spot interest rates). Finally, these spot interest rates are the interest rates represented in observed yield curves.

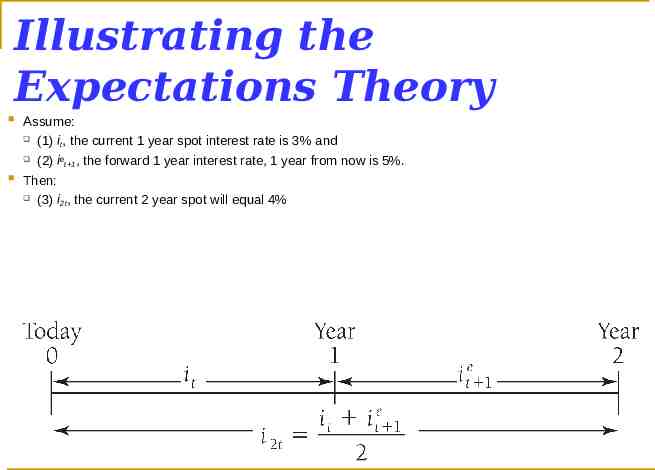
Expectations Theory: What Determines the Long Term Spot This theory assumes that the current long term spot Interest Rate interest rate which we can observe is comprised of 2 components (1) A current shorter term spot interest rate and (2) The expected, or forward, interest rate. Determine the 2-year spot rate assuming: (1) the current 1 year spot interest rate is 3% and (2) the forward 1 year interest rate, 1 year from now is 5%. Also, assume there is no risk of default and no required premium for longer term financial assets. Given the above, what will the market set as the current 2 year spot interest rate?

Solving for the Long Term Spot Interest Rate Recall, the one year rate is 3% and the expected 1 year rate one year from now (i.e., forward rate) is 5% Answer: The “equilibrium” 2 year spot rate is 4.0% Why? Because at 4%, the financial markets are “indifferent” to investing (or lending) for 1 year or 2 years. Note: A series of 2, one year instruments will offer an average annual return or 4% ( 3 5/2) while the 2 year instrument will offer an annual return of 4%.

Illustrating the Expectations Theory Assume: (1) i , the current 1 year spot interest rate is 3% and t (2) iet 1, the forward 1 year interest rate, 1 year from now is 5%. Then: (3) i , the current 2 year spot will equal 4% 2t

More Examples Assume the following: Current (spot) one year rate is 5% and The market’s forward one year rates over the next five years (years 2, 3, 4, and 5) are: Beginning of year 2: 6%, Beginning of year 3: 7%, Beginning of year 4: 8%, and Beginning of year 5: 9%. Given this data, calculate the following long term spot rates: Current (spot) two year bond rate Current (spot) five year bond rate

Market’s Long Term Spot Rates 2 Year Interest Rate: The market’s current rate on a two-year bond is calculated as follows: Current (spot)1 year rate is 5% and forward 1 year rate, 1 year from now is 6%, then: Current 2 year bond rate (5% 6%)/2 5.5% 5 year Interest Rate: The market’s current rate on a five-year bond is calculated as follows: Current (spot)1 year rate is 5% and forward 1 year rates, 1 year from now through five years from now are: 6%, 7%, 8%, and 9%, then: Current 5 year bond rate (5% 6% 7% 8% 9%)/5 7%

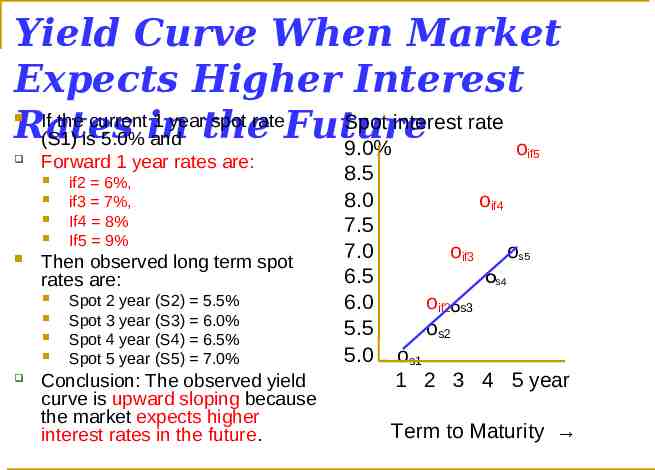
Expectations For Rising Interest Rates and the Observed Yield If interest rates are expected to rise in future, forward Curve rates will be above today's observed spot rates. And these higher forward rates will result in higher observed spot rates as we move out the maturity. Recall previous example: The current (spot)1 year rate was 5% and forward 1 year rate, 1 year from now was 6%. As a result the 2 year spot rate is 5.5% and is higher than the 1 year spot rate (5%) Yield Curve Question: Given the situation above where forward rates are higher than current spot rates (because the market expects higher rates in the future), what will the current yield curve look like?

Yield Curve When Market Expects Higher Interest If the current 1 year spot rate Spot interest rate Rates in the Future (S1) is 5.0% and 9.0% o Forward 1 year rates are: Then observed long term spot rates are: if2 6%, if3 7%, If4 8% If5 9% Spot 2 year (S2) 5.5% Spot 3 year (S3) 6.0% Spot 4 year (S4) 6.5% Spot 5 year (S5) 7.0% Conclusion: The observed yield curve is upward sloping because the market expects higher interest rates in the future. if5 8.5 8.0 7.5 7.0 6.5 6.0 5.5 5.0 oif4 oif3 os5 Os4 oif2Os3 os2 os1 1 2 3 4 5 year Term to Maturity

One More Example Now assume the following: Current (spot) one year rate is 9% and The market’s forward one year rates over the next five years (years 2, 3, 4, and 5) are: Beginning of year 2: 8%, Beginning of year 3: 7%, Beginning of year 4: 6%, and Beginning of year 5: 5%. Given this data, calculate the following long term spot rates: Current (spot) two year bond rate Current (spot) five year bond rate

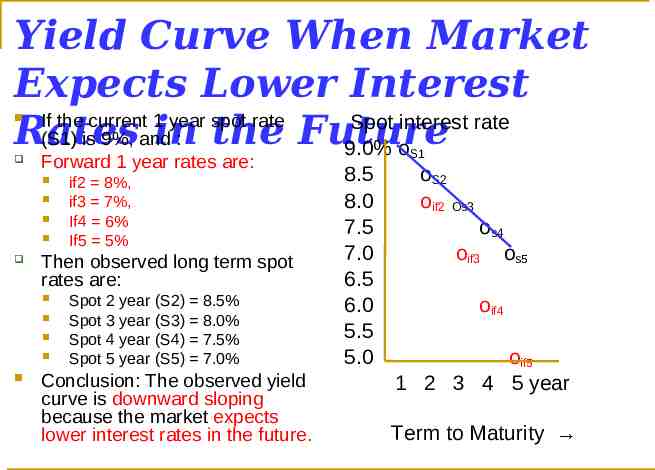
Expectations For Falling Interest Rates and the Observed Yield If interest rates are expected to fall in future, forward Curve rates will be below today's observed spot rates. And these lower forward rates will result in lower observed spot rates as we move out the maturity. Assume: The current (spot)1 year rate is 9% and forward 1 year rate, 1 year from now is 8% Given this information, the 2 year equilibrium spot rate is 8.5% (9% 8%)/2 8.5% Note: The 2 year spot rate is lower than the 1 year spot rate. Yield Curve Question: Given this situation where forward rates are lower than current spot rates (because the market expects lower rates in the future), what will the current yield curve look like?

Yield Curve When Market Expects Lower Interest If the current 1 year spot rate Spot interest rate Rates in the Future (S1) is 9%, and : 9.0% o Forward 1 year rates are: Then observed long term spot rates are: if2 8%, if3 7%, If4 6% If5 5% Spot 2 year (S2) 8.5% Spot 3 year (S3) 8.0% Spot 4 year (S4) 7.5% Spot 5 year (S5) 7.0% Conclusion: The observed yield curve is downward sloping because the market expects lower interest rates in the future. S1 8.5 8.0 7.5 7.0 6.5 6.0 5.5 5.0 oS2 oif2 Os3 os4 oif3 os5 oif4 oif5 1 2 3 4 5 year Term to Maturity

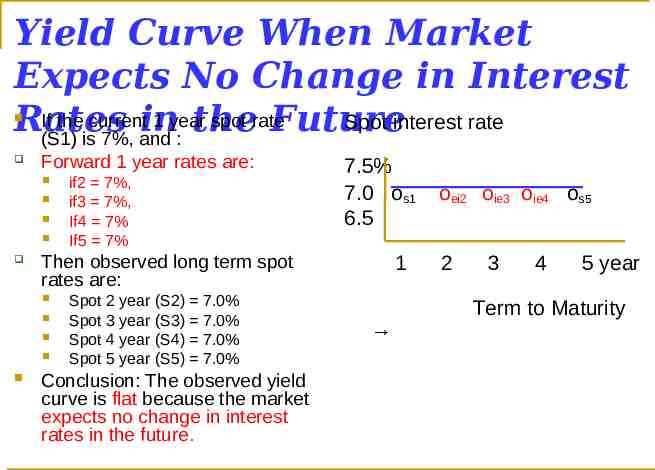
Yield Curve When Market Expects No Change in Interest If the currentin 1 year spot rate Spot interest rate Rates the Future (S1) is 7%, and : Forward 1 year rates are: 1 Then observed long term spot rates are: if2 7%, if3 7%, If4 7% If5 7% 7.5% 7.0 os1 6.5 Spot 2 year (S2) 7.0% Spot 3 year (S3) 7.0% Spot 4 year (S4) 7.0% Spot 5 year (S5) 7.0% Conclusion: The observed yield curve is flat because the market expects no change in interest rates in the future. oei2 oie3 oie4 os5 2 3 4 5 year Term to Maturity

Summary of Expectations Regarding Future Interest The shape and slope of the yield curve reflects the Rates markets’ expectations about future interest rates. Upward Sloping (Ascending, Positive) Yield Curves: Future (forward) interest rates are expected to increase above existing spot rates. Downward Sloping (Descending, Inverted, Negative) Yield Curves: Future (forward) interest rates are expected to decrease below existing spot rates. Flat Yield Curves Future (forward) interest rates are expected to remain the same as existing spot rates.

Appendix 1 Yield Curve web sites.

Yield Curves on Line Visit the following sites: (1) Bloomberg: U.S. Treasury and Selected Foreign Country Yield Curves (2) Dynamic U.S. Treasury Yield Curve http://stockcharts.com/charts/yieldcurve.html You can view yield curve changes over time. (3)Yield Curves for Treasuries and Corporates http://www.bloomberg.com/markets/rates/index.html http://www.bondsonline.com/Todays Market/ Composite Bond Yields.php (4) Nominal and Real U.S. Treasury Yield Curves http://www.treasury.gov/resource-center/data-chart-center/ interest-rates/Pages/Historic-Yield-Data-Visualization.aspx

Yield Curves for Foreign Countries United Kingdom (and U.S.) http://www.yieldcurve.com/marketyieldcurve.asp Euro-Zone http://www.ecb.int/stats/money/yc/html/index.en.html This site lets you compare UK and US yield curves. Note: Select “spot rate” curve for current Euro-zone yield curve Other countries: http://www.bloomberg.com/ Link to Markets, then to Government Bonds (current yield curves for U.K., UK, Germany, Japan, Australia and Brazil)