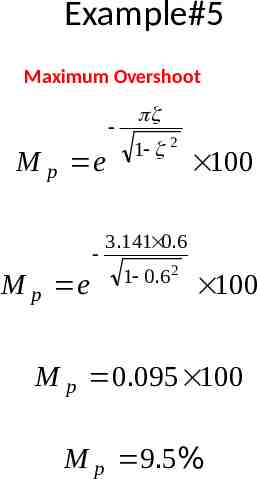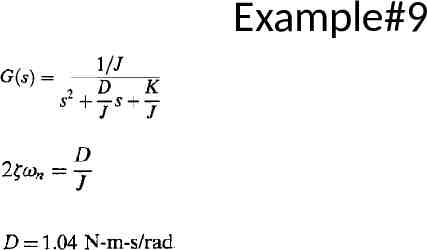Feedback Control Systems (FCS) Lecture-22-23-24 Time Domain

Feedback Control Systems (FCS) Lecture-22-23-24 Time Domain Analysis of 2nd Order Systems Dr. Imtiaz Hussain email: [email protected] URL :http://imtiazhussainkalwar.weebly.com/

Introduction We have already discussed the affect of location of poles and zeros on the transient response of 1st order systems. Compared to the simplicity of a first-order system, a second-order system exhibits a wide range of responses that must be analyzed and described. Varying a first-order system's parameter (T, K) simply changes the speed and offset of the response Whereas, changes in the parameters of a second-order system can change the form of the response. A second-order system can display characteristics much like a first-order system or, depending on component values, display damped or pure oscillations for its transient response.

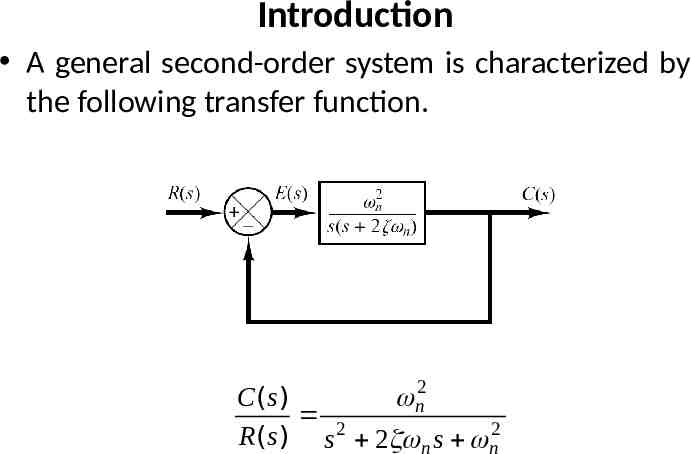
Introduction A general second-order system is characterized by the following transfer function. n2 C (s ) 2 R(s ) s 2 n s n2

Introduction n2 C (s ) 2 R(s ) s 2 n s n2 n un-damped natural frequency of the second order system, which is the frequency of oscillation of the system without damping. damping ratio of the second order system, which is a measure of the degree of resistance to change in the system output.

Example#1 Determine the un-damped natural frequency and damping ratio of the following second order system. C (s ) 4 2 R( s ) s 2 s 4 Compare the numerator and denominator of the given transfer function with the general 2nd order transfer function. n2 C (s ) 2 R(s ) s 2 n s n2 n2 4 n 2 rad / sec s 2 2 n s n2 s 2 2s 4 2 n s 2 s n 1 0.5

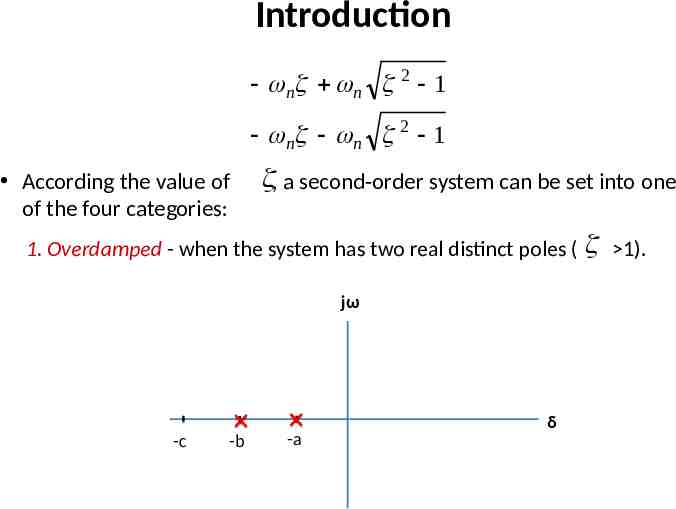
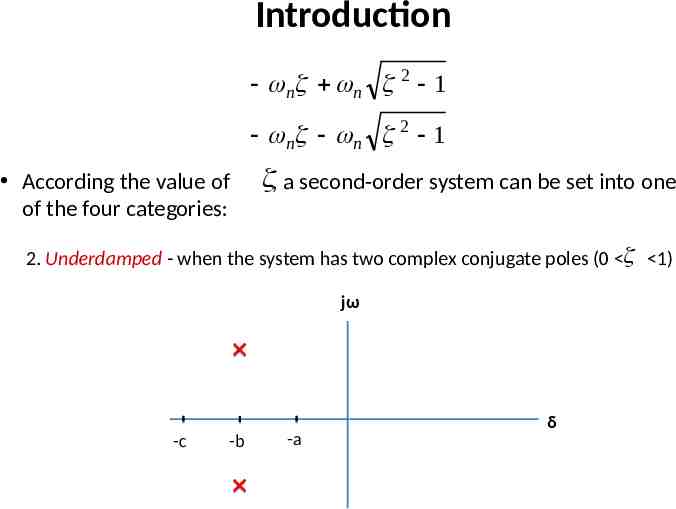
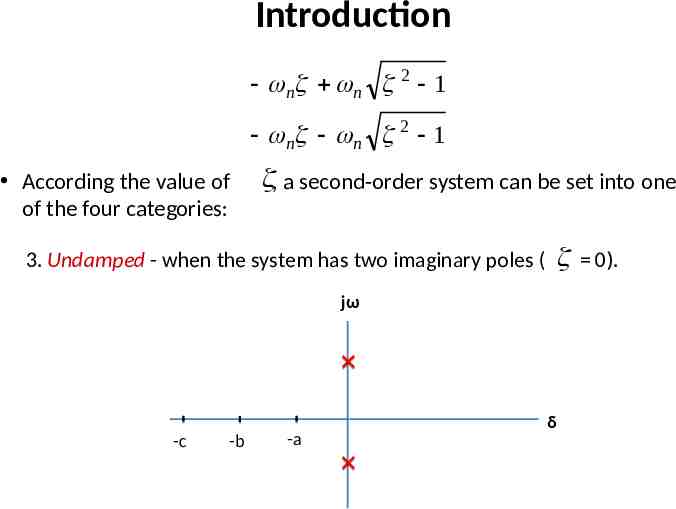
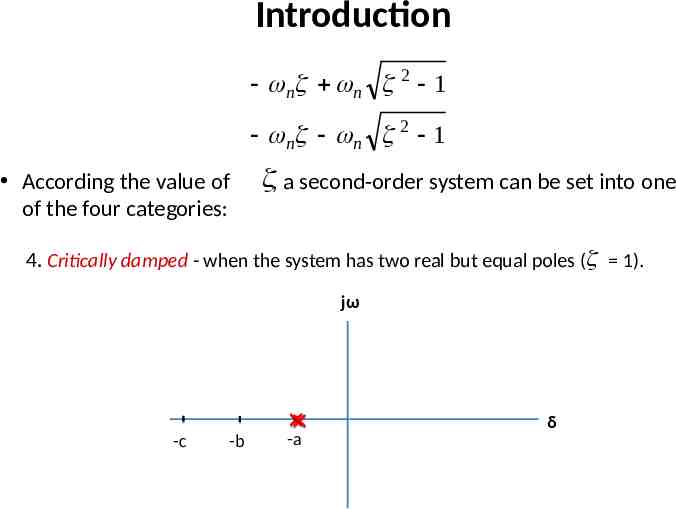
Introduction n2 C (s ) 2 R(s ) s 2 n s n2 Two poles of the system are n n 2 1 n n 2 1

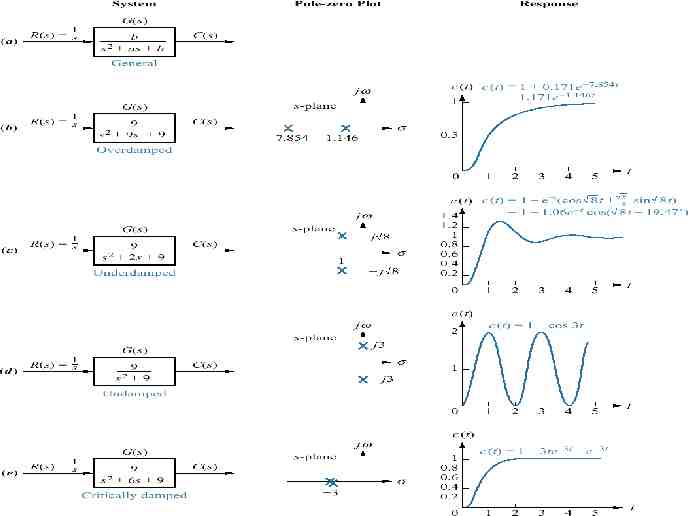
Introduction n n 2 1 n n 2 1 According the value of of the four categories: , a second-order system can be set into one 1. Overdamped - when the system has two real distinct poles ( 1). jω -c -b -a δ

Introduction n n 2 1 n n 2 1 According the value of of the four categories: , a second-order system can be set into one 2. Underdamped - when the system has two complex conjugate poles (0 1) jω -c -b -a δ

Introduction n n 2 1 n n 2 1 According the value of of the four categories: , a second-order system can be set into one 3. Undamped - when the system has two imaginary poles ( jω -c -b -a δ 0).

Introduction n n 2 1 n n 2 1 According the value of of the four categories: , a second-order system can be set into one 4. Critically damped - when the system has two real but equal poles ( 1). jω -c -b -a δ

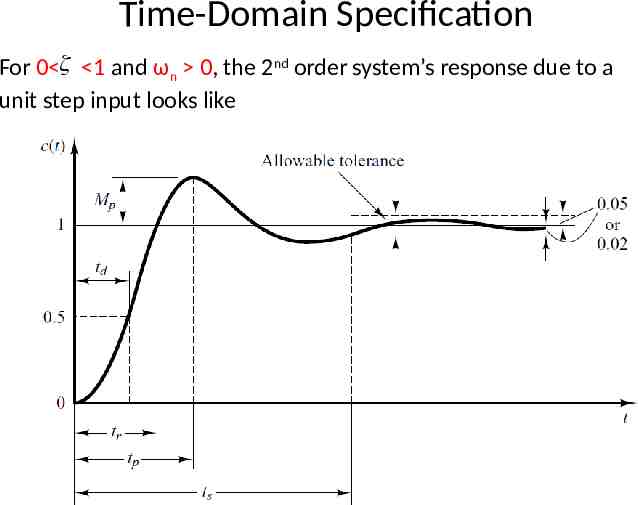
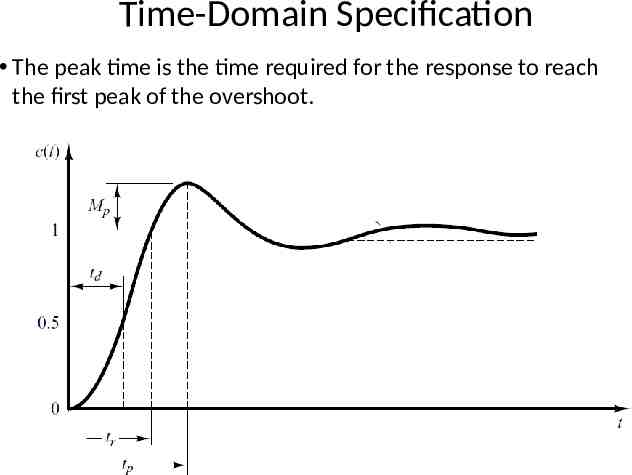
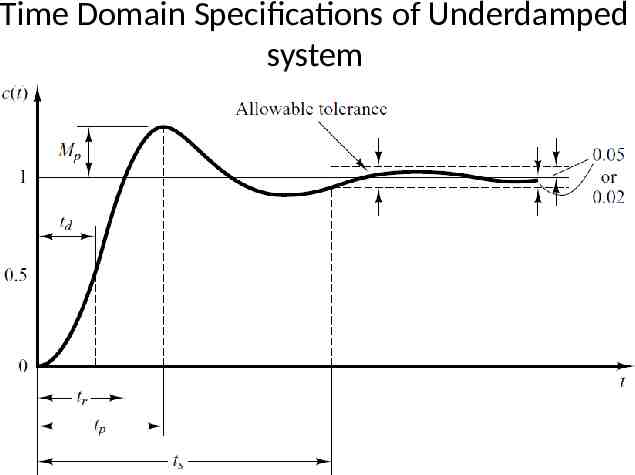
Time-Domain Specification For 0 1 and ωn 0, the 2nd order system’s response due to a unit step input looks like 11

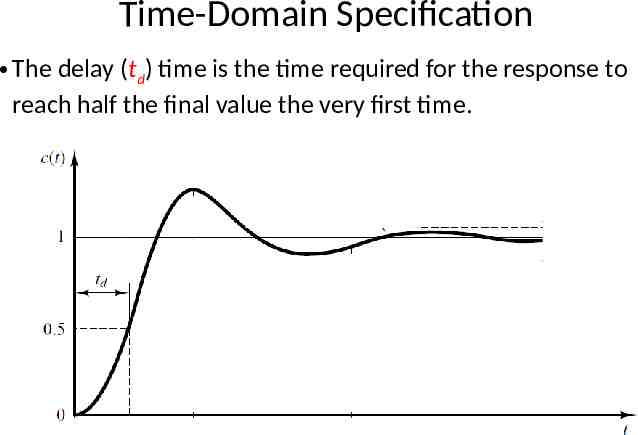
Time-Domain Specification The delay (td) time is the time required for the response to reach half the final value the very first time. 12

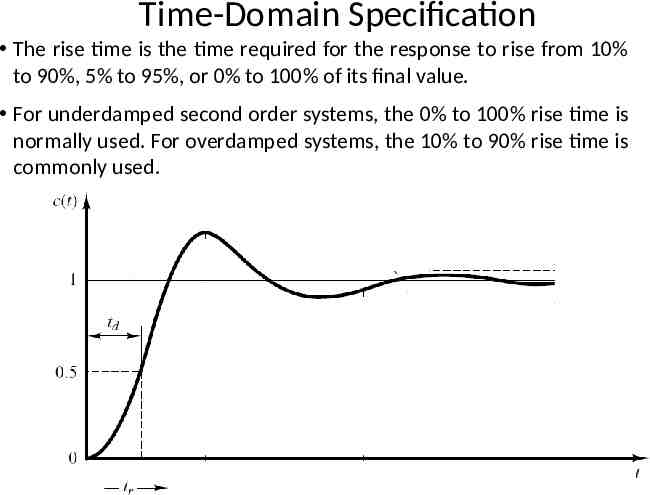
Time-Domain Specification The rise time is the time required for the response to rise from 10% to 90%, 5% to 95%, or 0% to 100% of its final value. For underdamped second order systems, the 0% to 100% rise time is normally used. For overdamped systems, the 10% to 90% rise time is commonly used.

Time-Domain Specification The peak time is the time required for the response to reach the first peak of the overshoot. 14 14

Time-Domain Specification The maximum overshoot is the maximum peak value of the response curve measured from unity. If the final steady-state value of the response differs from unity, then it is common to use the maximum percent overshoot. It is defined by The amount of the maximum (percent) overshoot directly indicates the relative stability of the system. 15

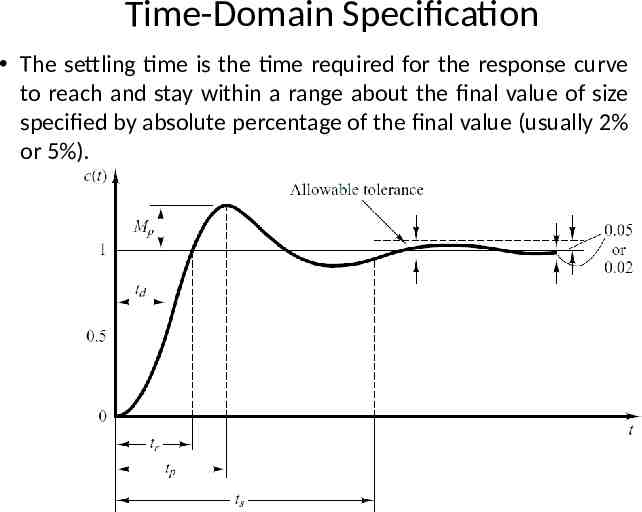
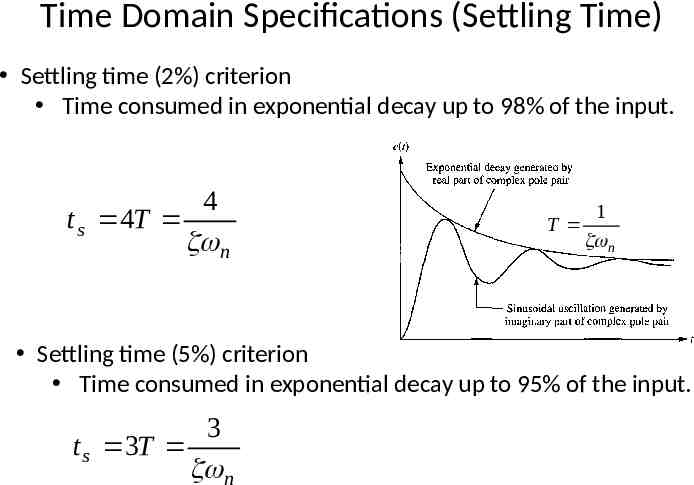
Time-Domain Specification The settling time is the time required for the response curve to reach and stay within a range about the final value of size specified by absolute percentage of the final value (usually 2% or 5%). 16

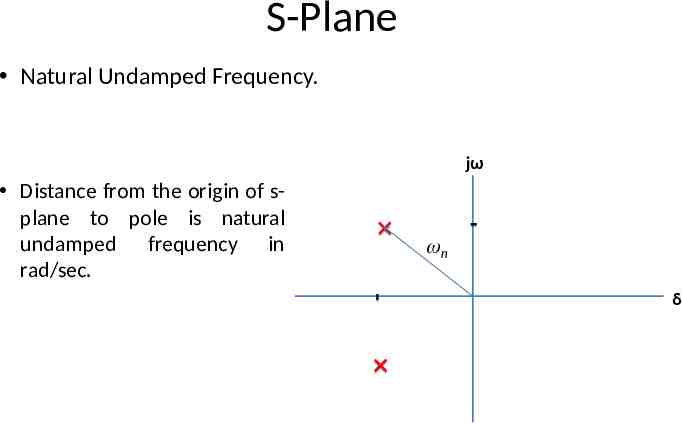
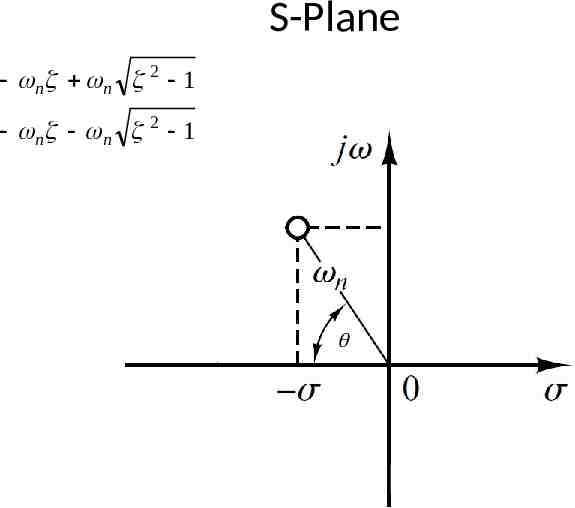
S-Plane Natural Undamped Frequency. jω Distance from the origin of splane to pole is natural undamped frequency in rad/sec. n δ

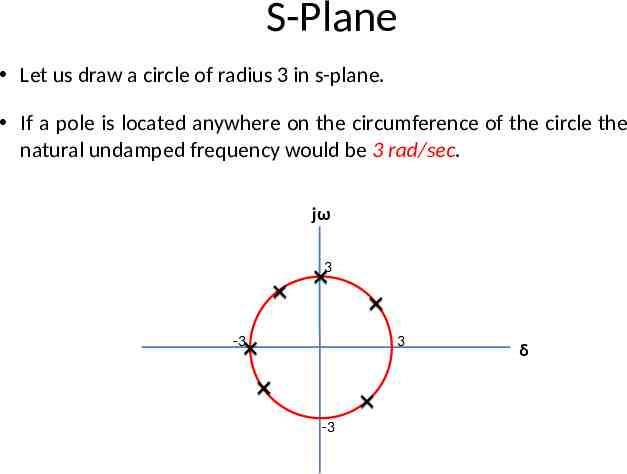
S-Plane Let us draw a circle of radius 3 in s-plane. If a pole is located anywhere on the circumference of the circle the natural undamped frequency would be 3 rad/sec. jω 3 -3 3 -3 δ

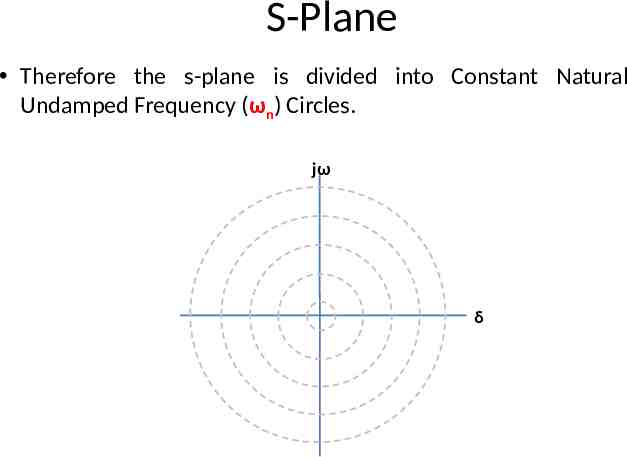
S-Plane Therefore the s-plane is divided into Constant Natural Undamped Frequency (ωn) Circles. jω δ

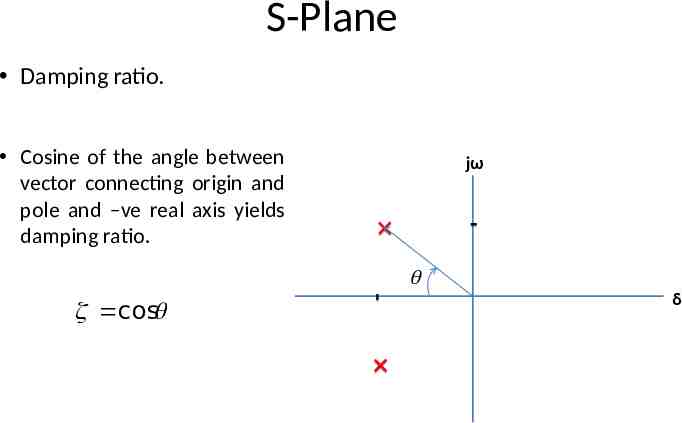
S-Plane Damping ratio. Cosine of the angle between vector connecting origin and pole and –ve real axis yields damping ratio. jω cos δ

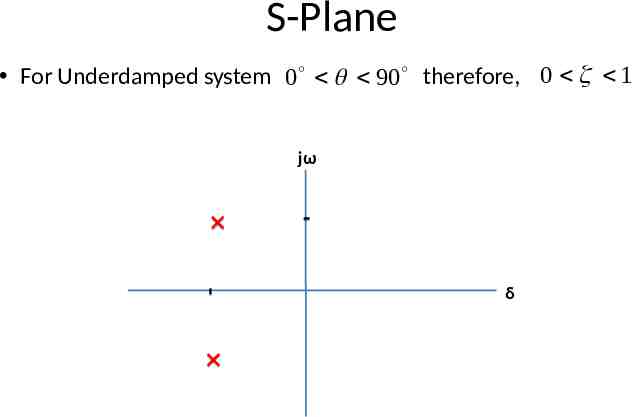
S-Plane For Underdamped system 0 90 therefore, 0 1 jω δ

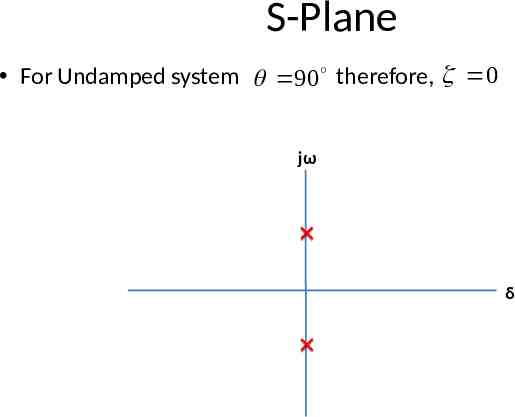
S-Plane For Undamped system 90 therefore, 0 jω δ

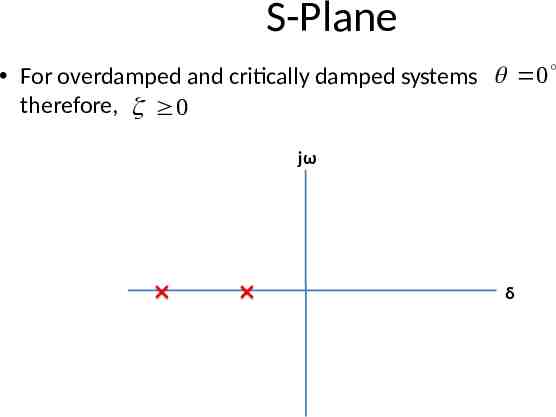
S-Plane For overdamped and critically damped systems 0 therefore, 0 jω δ

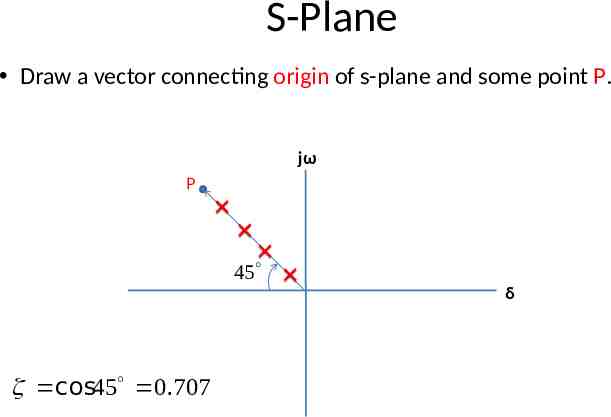
S-Plane Draw a vector connecting origin of s-plane and some point P. jω P 45 δ cos45 0.707

S-Plane Therefore, s-plane is divided into sections of constant damping ratio lines. jω δ

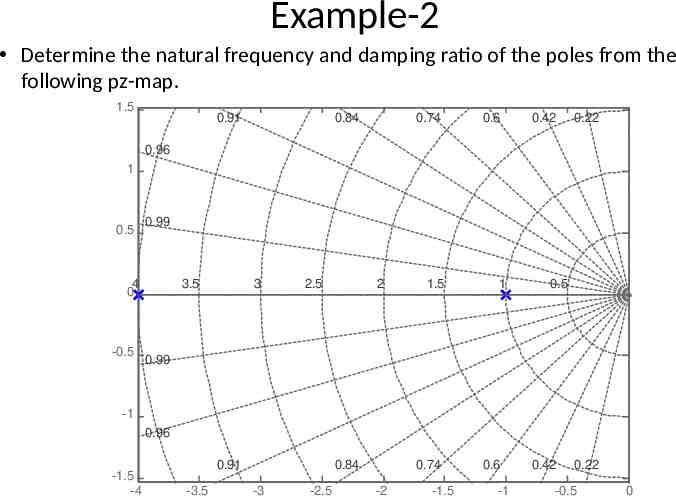
Example-2 Determine the natural frequency and damping ratio of the poles from the following pz-map. Pole-Zero Map 1.5 0.91 0.84 0.74 0.6 0.42 0.22 0.96 Imaginary Axis (seconds-1) 1 0.5 0.99 4 0 -0.5 3.5 3 2.5 2 1.5 1 0.5 0.99 -1 0.96 -1.5 -4 0.91 -3.5 0.84 -3 -2.5 0.74 -2 -1.5 -1 0.6 -1 0.42 0.22 -0.5 0

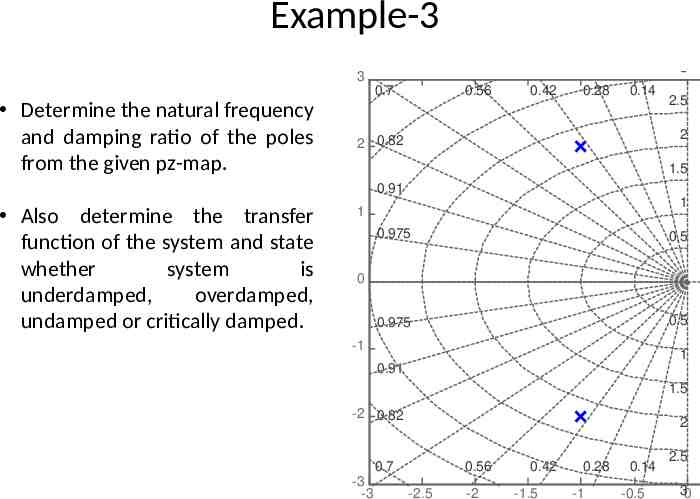
Example-3 Pole-Zero Map 3 Determine the natural frequency and damping ratio of the poles from the given pz-map. 0.7 0.56 0.42 0.28 0.14 2.5 2 2 0.82 1.5 Imaginary Axis (seconds-1) 0.91 Also determine the transfer function of the system and state whether system is underdamped, overdamped, undamped or critically damped. 3 1 1 0.975 0.5 0.975 0.5 0 -1 1 0.91 1.5 -2 0.82 2 0.7 -3 -3 0.56 -2.5 -2 0.42 -1.5 0.28 -1 0.14 -0.5 2.5 30

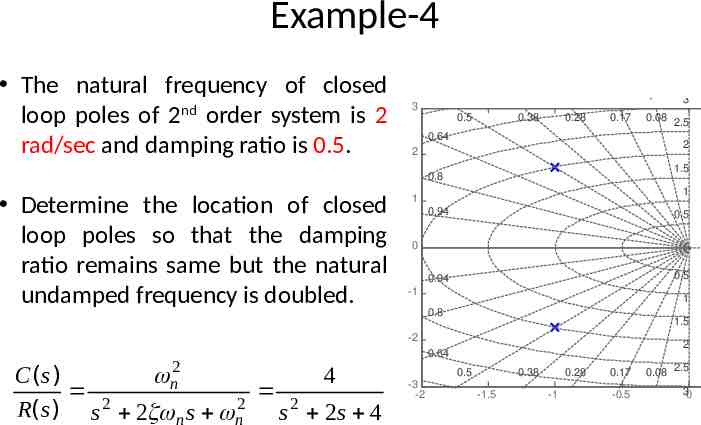
Example-4 The natural frequency of closed loop poles of 2nd order system is 2 rad/sec and damping ratio is 0.5. Pole-Zero Map 3 0.5 0.38 0.28 0.17 0.64 1.5 Imaginary Axis 1 1 0.94 0.5 0.94 0.5 0 -1 1 0.8 1.5 -2 n2 C (s ) 4 2 2 2 R(s ) s 2 n s n s 2s 4 0.08 2.5 2 2 0.8 Determine the location of closed loop poles so that the damping ratio remains same but the natural undamped frequency is doubled. 3 2 0.64 0.5 -3 -2 0.38 -1.5 0.28 -1 0.17 0.08 2.5 -0.5 30 Real Axis

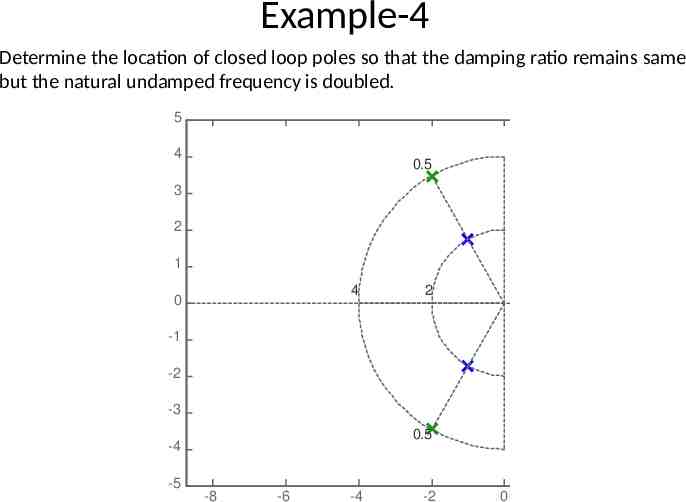
Example-4 Determine the location of closed loop poles so that the damping ratio remains same but the natural undamped frequency is doubled. Pole-Zero Map 5 4 0.5 3 Imaginary Axis 2 1 4 0 2 -1 -2 -3 0.5 -4 -5 -8 -6 -4 -2 0 2 4

S-Plane n n 2 1 n n 2 1

Step Response of underdamped System n2 C (s ) 2 R(s ) s 2 n s n2 Step Response C (s ) n2 s s 2 2 n s n2 The partial fraction expansion of above equation is given as s 2 n 1 C (s ) 2 s s 2 n s n2 n2 1 2 s 2 n 2 s 2 n 1 C (s ) 2 s s 2 n s 2 n2 n2 2 n2 s 2 n 1 C (s ) s s n 2 n2 1 2

Step Response of underdamped System s 2 n 1 C (s ) s s n 2 n2 1 2 Above equation can be written as s 2 n 1 C (s ) s s n 2 d2 Where d n 1 2 , is the frequency of transient oscillations and is called damped natural frequency. The inverse Laplace transform of above equation can be obtained easily if C(s) is written in the following form: s n n 1 C (s ) 2 2 s s n d s n 2 d2

Step Response of underdamped System s n n 1 C (s ) 2 2 s s n d s n 2 d2 s n 1 C (s ) 2 2 s s n d s n 1 C (s ) 2 2 s s n d c(t ) 1 e n t cos d t 1 2 n 1 2 s n 2 d2 d 1 1 2 2 s n 2 d2 e n t sin d t

Step Response of underdamped System c(t ) 1 e n t cos d t 1 2 e nt sin d t c(t ) 1 e n t cos d t sin d t 2 1 When 0 d n 1 2 n c(t ) 1 cos n t

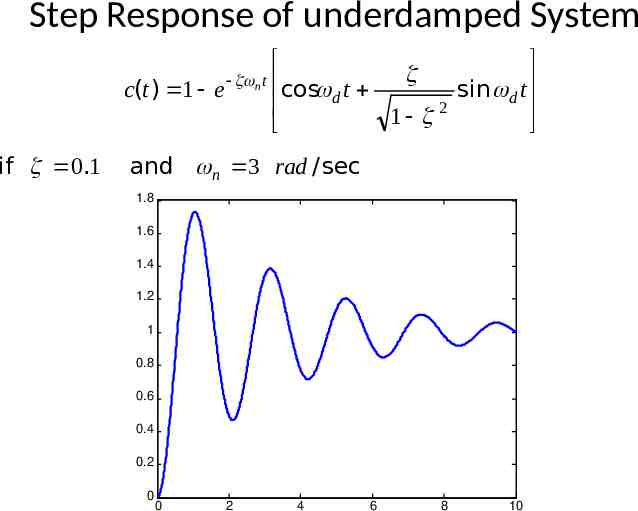
Step Response of underdamped System c(t ) 1 e n t cos d t sin d t 2 1 if 0.1 and n 3 rad / sec 1.8 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 0 0 2 4 6 8 10

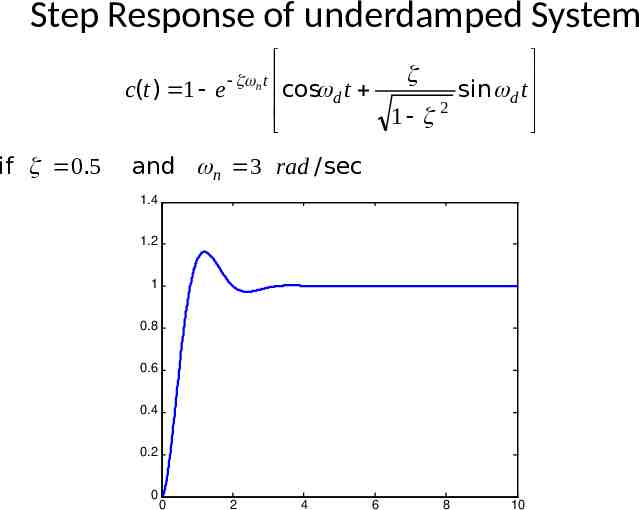
Step Response of underdamped System c(t ) 1 e n t cos d t sin d t 2 1 if 0.5 and n 3 rad / sec 1.4 1.2 1 0.8 0.6 0.4 0.2 0 0 2 4 6 8 10

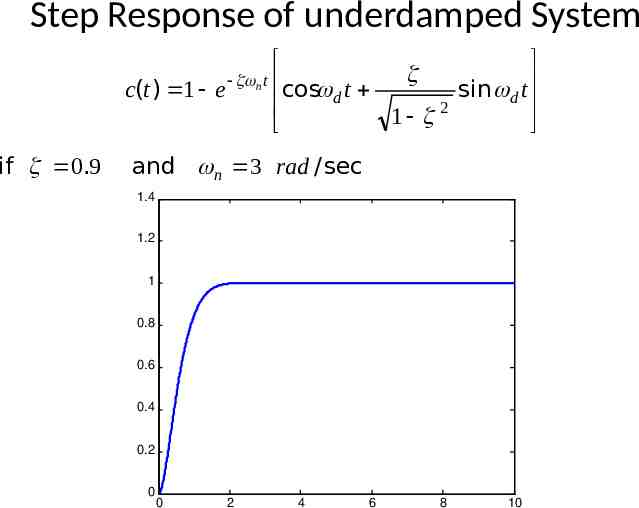
Step Response of underdamped System c(t ) 1 e n t cos d t sin d t 2 1 if 0.9 and n 3 rad / sec 1.4 1.2 1 0.8 0.6 0.4 0.2 0 0 2 4 6 8 10

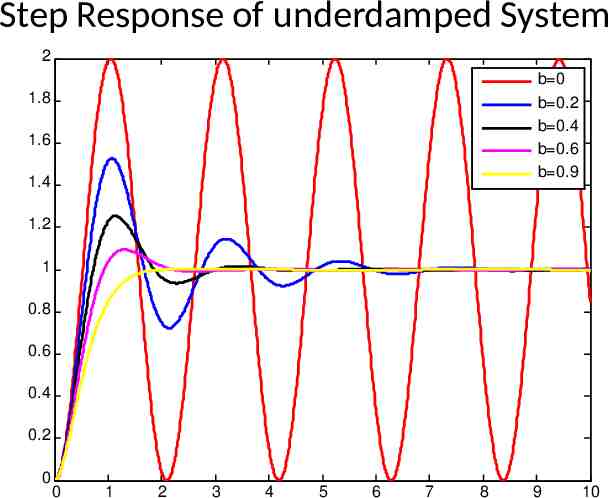
Step Response of underdamped System 2 b 0 b 0.2 b 0.4 b 0.6 b 0.9 1.8 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 0 0 1 2 3 4 5 6 7 8 9 10

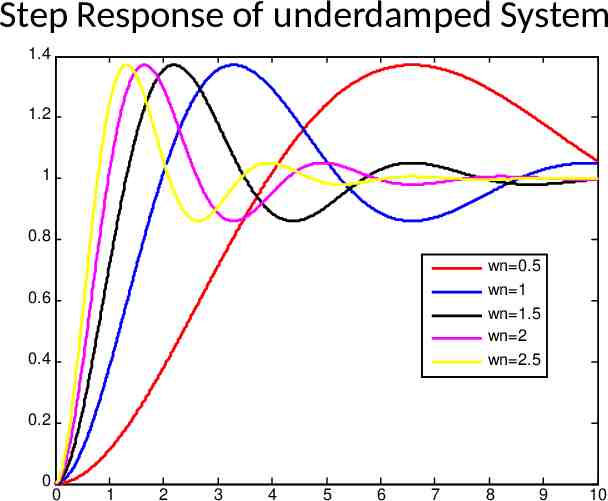
Step Response of underdamped System 1.4 1.2 1 0.8 wn 0.5 wn 1 wn 1.5 wn 2 wn 2.5 0.6 0.4 0.2 0 0 1 2 3 4 5 6 7 8 9 10

Time Domain Specifications of Underdamped system

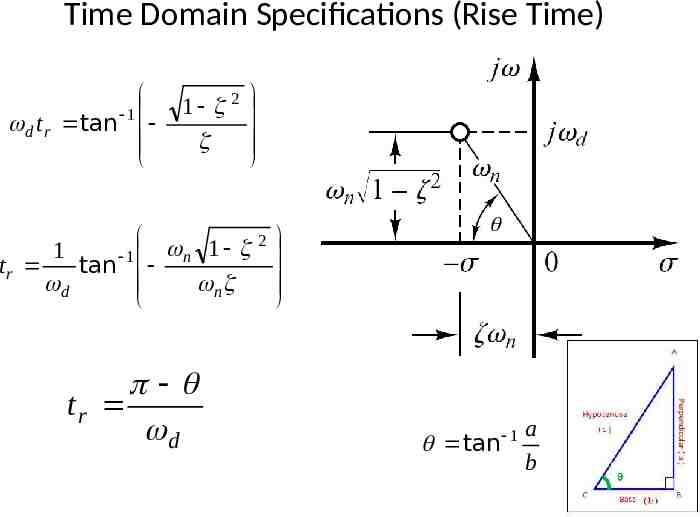
Time Domain Specifications (Rise Time) c(t ) 1 e n t cos d t sin d t 2 1 Put t t r in above equation c(t r ) 1 e nt r cos d t r sin d t r 2 1 Where c(t r ) 1 0 e n t r cos d t r sin d t r 2 1 e nt r 0 0 cos d t r sin d t r 2 1

Time Domain Specifications (Rise Time) cos d t r sin d t r 0 2 1 above equation can be re - writen as sin d t r 1 2 cos d t r tan d t r d t r tan 1 1 2 1 2

Time Domain Specifications (Rise Time) d t r tan 1 1 2 1 2 1 tr tan 1 n d n tr d tan 1 a b

Time Domain Specifications (Peak Time) c(t ) 1 e n t cos d t 1 2 sin d t In order to find peak time let us differentiate above equation w.r.t t. dc(t ) n t t d n e cos d t sin d t e n d sin d t cos d t dt 1 2 1 2 0 e n t n cos d t 2 n 1 2 sin d t d sin d t d 1 2 cos d t 2 2 1 n n 0 e nt n cos d t sin d t d sin d t cos d t 2 2 1 1

Time Domain Specifications (Peak Time) 2 2 1 n t n n 0 e n cos d t sin d t d sin d t cos d t 2 2 1 1 2 n e nt sin d t d sin d t 0 1 2 e nt 0 2 n sin d t d sin d t 0 1 2 2 n sin d t d 0 1 2

Time Domain Specifications (Peak Time) 2 n sin d t d 0 1 2 2 n d 0 1 2 sin d t 0 d t sin 1 0 0, , 2 , t d Since for underdamped stable systems first peak is maximum peak therefore, tp d

Time Domain Specifications (Maximum Overshoot) c(t p ) 1 e n t p cos d t p sin d t p 2 1 c( ) 1 t M p 1 e n p cos d t p sin d t p 2 1 Put 1 100 tp in above equation d n d M p e cos sin 100 d d 2 d d 1

Time Domain Specifications (Maximum Overshoot) n d M p e Put cos sin 100 d d 2 d d 1 ωd ωn 1-ζ 2 in above equation n n M p e 1 2 M p e cos 100 sin 2 1 1 2 M p e 1 0 100 1 2 100

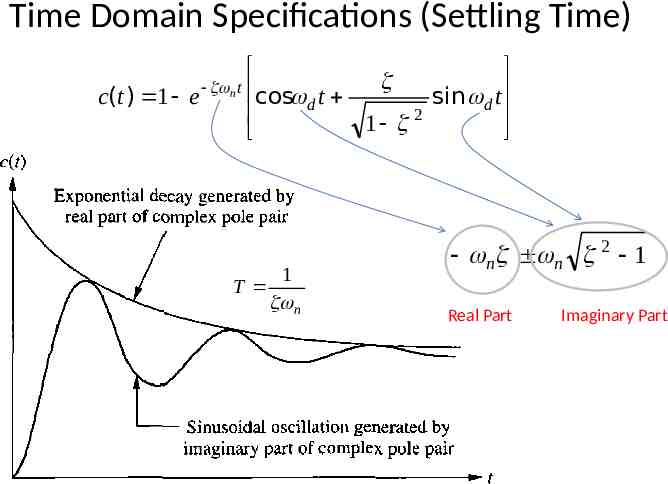
Time Domain Specifications (Settling Time) c(t ) 1 e nt cos d t sin d t 2 1 T 1 n n n 2 1 Real Part Imaginary Part

Time Domain Specifications (Settling Time) Settling time (2%) criterion Time consumed in exponential decay up to 98% of the input. 4 t s 4T n T 1 n Settling time (5%) criterion Time consumed in exponential decay up to 95% of the input. 3 t s 3T n

Summary of Time Domain Specifications Rise Time tr 2 d n 1 Peak Time tp d 1 2 n Settling Time (2%) 4 t s 4T n 3 t s 3T n Settling Time (4%) Maximum Overshoot M p e 1 2 100

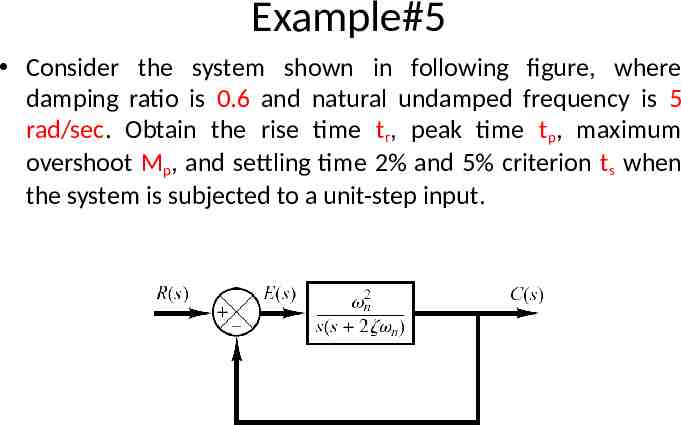
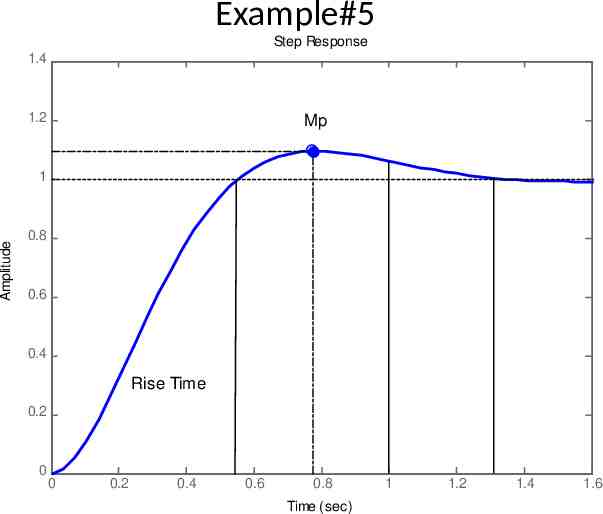
Example#5 Consider the system shown in following figure, where damping ratio is 0.6 and natural undamped frequency is 5 rad/sec. Obtain the rise time tr, peak time tp, maximum overshoot Mp, and settling time 2% and 5% criterion ts when the system is subjected to a unit-step input.

Example#5 Rise Time Peak Time tp d tr d Settling Time (2%) 4 t s 4T n 3 t s 3T n Settling Time (4%) Maximum Overshoot M p e 1 2 100

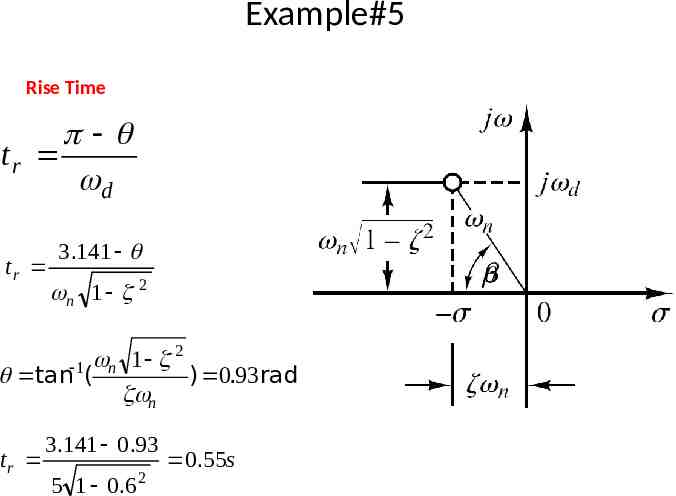
Example#5 Rise Time tr d tr 3.141 n 1 2 2 1 tan 1( n ) 0.93 rad n tr 3.141 0.93 5 1 0.6 2 0.55s

Example#5 Peak Time Settling Time (2%) 4 ts n tp d 3.141 tp 0.785s 4 4 ts 1.33s 0.6 5 Settling Time (4%) 3 ts n 3 ts 1s 0.6 5

Example#5 Maximum Overshoot M p e M p e 1 2 100 3.141 0.6 1 0.6 2 100 M p 0.095 100 M p 9.5%

Example#5 Step Response 1.4 1.2 Mp Amplitude 1 0.8 0.6 0.4 Rise Time 0.2 0 0 0.2 0.4 0.6 0.8 Time (sec) 1 1.2 1.4 1.6

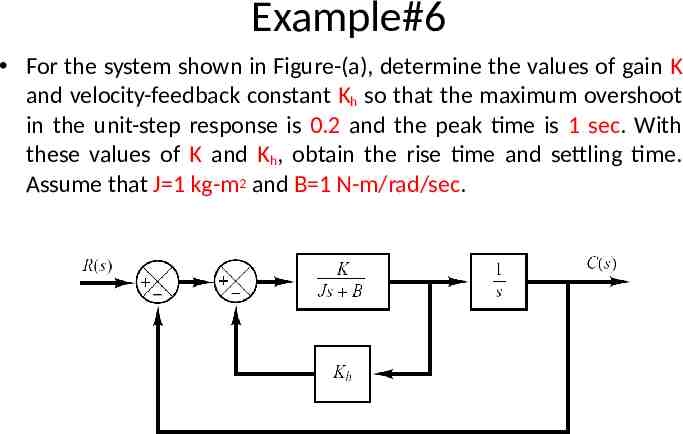
Example#6 For the system shown in Figure-(a), determine the values of gain K and velocity-feedback constant Kh so that the maximum overshoot in the unit-step response is 0.2 and the peak time is 1 sec. With these values of K and Kh, obtain the rise time and settling time. Assume that J 1 kg-m2 and B 1 N-m/rad/sec.

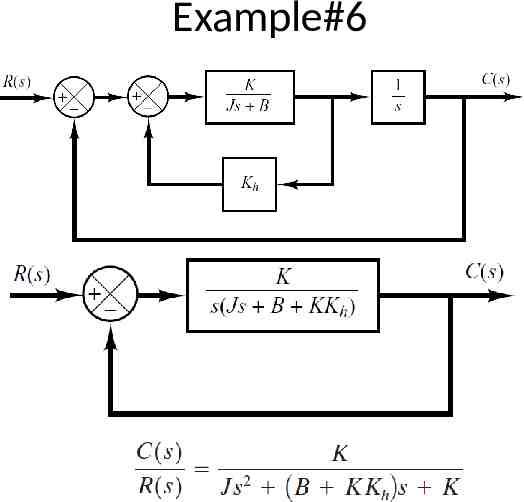
Example#6

Example#6 Since J 1 kgm 2 and B 1 Nm/rad/sec C (s ) K 2 R(s ) s (1 KK h )s K Comparing above T.F with general 2nd order T.F n2 C (s ) 2 R(s ) s 2 n s n2 n K (1 KK h ) 2 K

Example#6 n K Maximum overshoot is 0.2. (1 KK h ) 2 K The peak time is 1 sec tp d 1 ln(e 1 2 3.141 n 1 2 ) ln 0.2 n 3.141 1 0.4562 n 3.53

Example#6 n 3.96 n K 3.53 K 3.532 K K 12.5 (1 KK h ) 2 K 0.456 2 12.5 (1 12.5K h ) K h 0.178

Example#6 n 3.96 tr 4 ts n n 1 2 t s 2.48s t r 0.65s 3 ts n t s 1.86 s

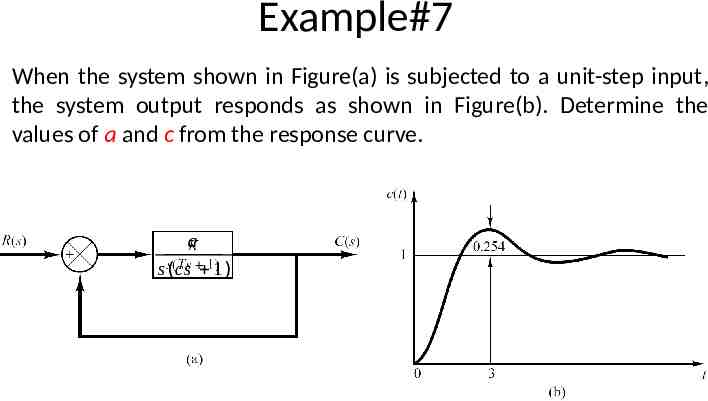
Example#7 When the system shown in Figure(a) is subjected to a unit-step input, the system output responds as shown in Figure(b). Determine the values of a and c from the response curve. a s ( cs 1)

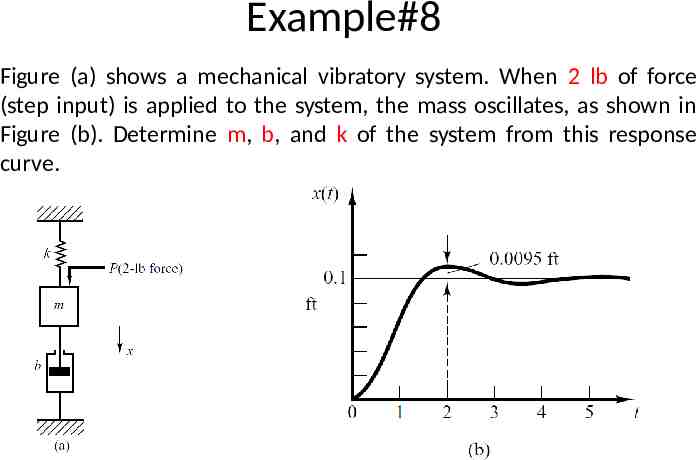
Example#8 Figure (a) shows a mechanical vibratory system. When 2 lb of force (step input) is applied to the system, the mass oscillates, as shown in Figure (b). Determine m, b, and k of the system from this response curve.

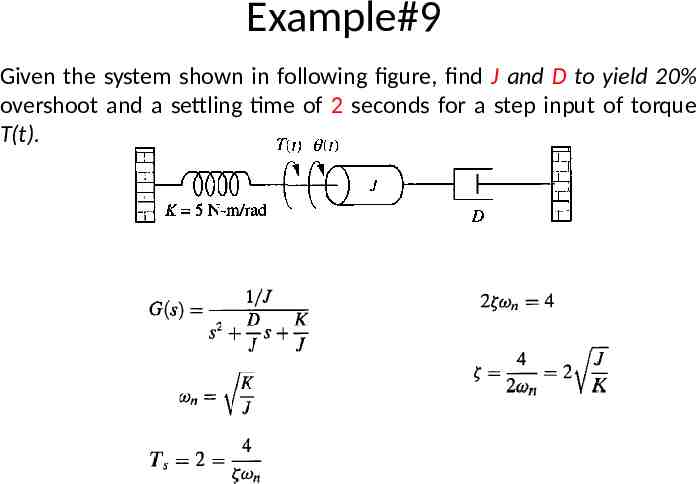
Example#9 Given the system shown in following figure, find J and D to yield 20% overshoot and a settling time of 2 seconds for a step input of torque T(t).

Example#9

Example#9

Step Response of critically damped System ( n2 C (s ) R( s ) s n 2 Step Response C (s ) 1 n2 s s n The partial fraction expansion of above equation is given as n2 s s n 2 A B C s s n s n 2 n 1 1 C (s ) s s n s n 2 c(t ) 1 e nt n e nt t c(t ) 1 e nt 1 n t 2 )

Step Response of overdamped and undamped Systems Home Work

71

Second – Order System Example 10: Describe the nature of the second-order system response via the value of the damping ratio for the systems with transfer function 12 1. G ( s ) 2 s 8 s 12 16 2. G ( s ) 2 s 8s 16 Do them as your own revision 20 3. G ( s ) 2 s 8 s 20 72

To download this lecture visit http://imtiazhussainkalwar.weebly.com/ END OF LECTURES-22-23-24