ELECTRIC MOTORS & GENERATORS Andrew Holliday

ELECTRIC MOTORS & GENERATORS Andrew Holliday

Motors and Generators Simple devices that use basic principles of electromagnetic theory Technologically important Motors drive everything from hybrid cars to vibrating phones. Most electrical power is provided by generators Work on the same principles: converting between mechanical and electrical energy using the magnetic force

Electric and Magnetic Fields Electric and magnetic fields are vector fields A vector has magnitude and direction A vector field describes a vector for every point in space

Electric Force An electric field exerts force on electric charge. The force is in the direction of the field - charges get pushed in the direction of the field. F qE (q is magnitude of charge).

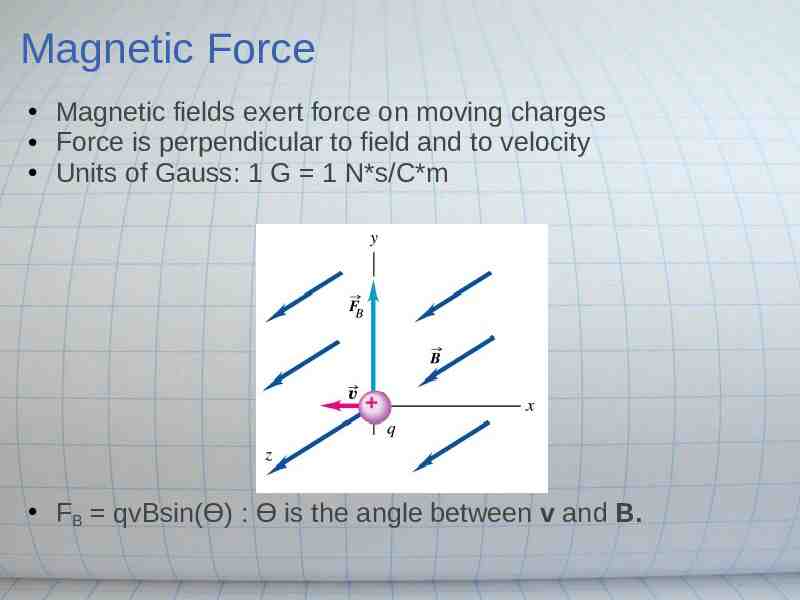
Magnetic Force Magnetic fields exert force on moving charges Force is perpendicular to field and to velocity Units of Gauss: 1 G 1 N*s/C*m FB qvBsin(ϴ) : ϴ is the angle between v and B.

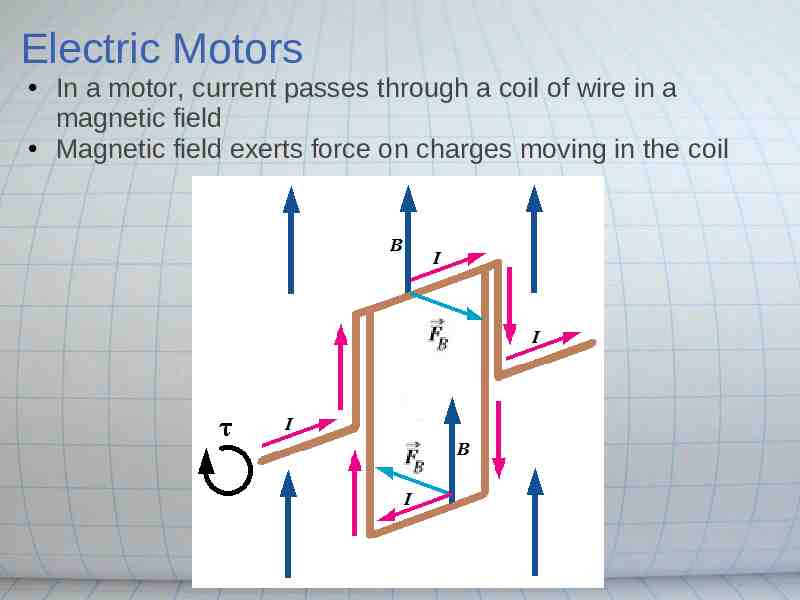
Electric Motors In a motor, current passes through a coil of wire in a magnetic field Magnetic field exerts force on charges moving in the coil

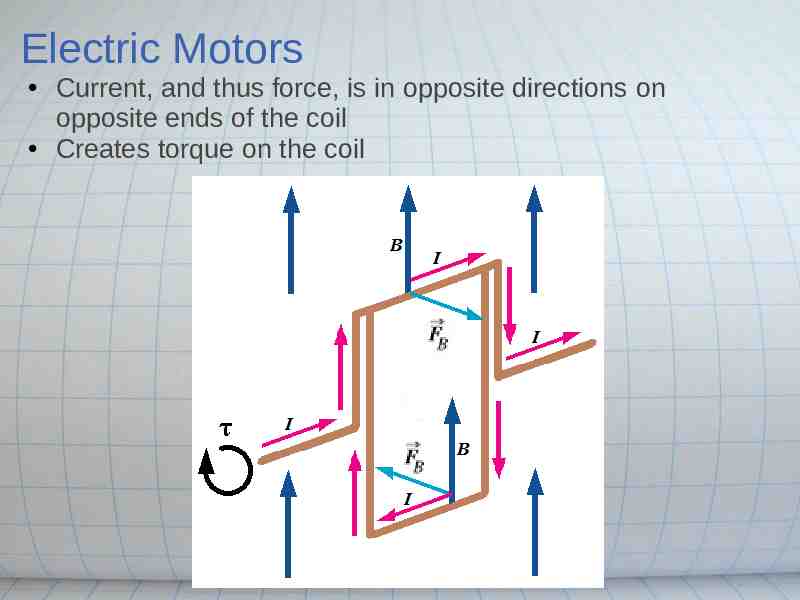
Electric Motors Current, and thus force, is in opposite directions on opposite ends of the coil Creates torque on the coil

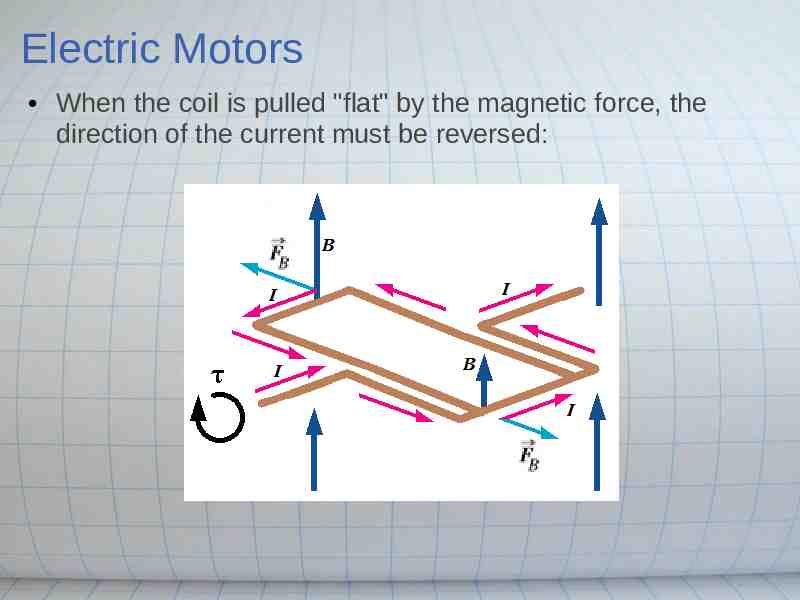
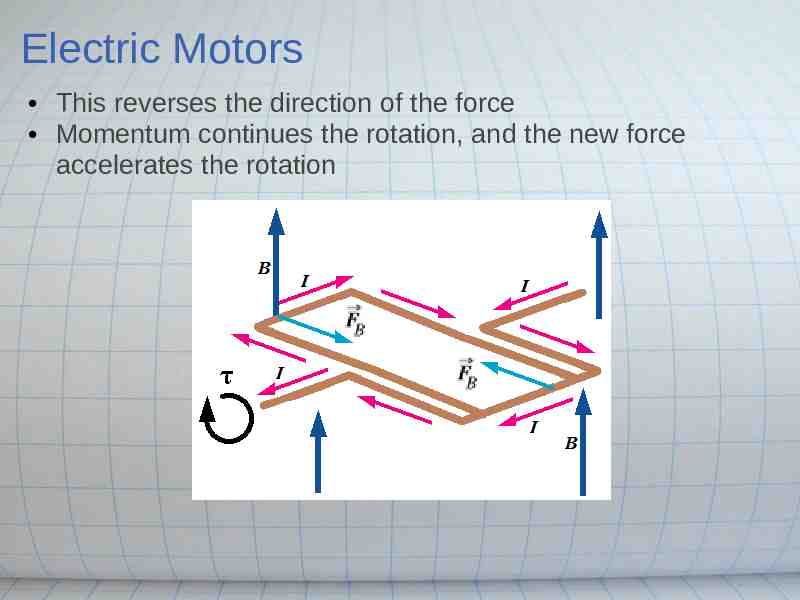
Electric Motors When the coil is pulled "flat" by the magnetic force, the direction of the current must be reversed:

Electric Motors This reverses the direction of the force Momentum continues the rotation, and the new force accelerates the rotation

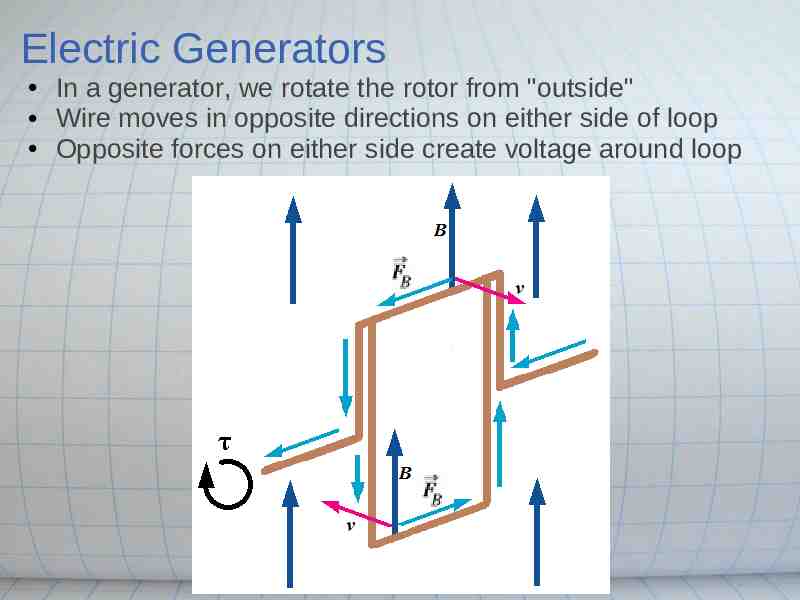
Electric Generators In a generator, we rotate the rotor from "outside" Wire moves in opposite directions on either side of loop Opposite forces on either side create voltage around loop

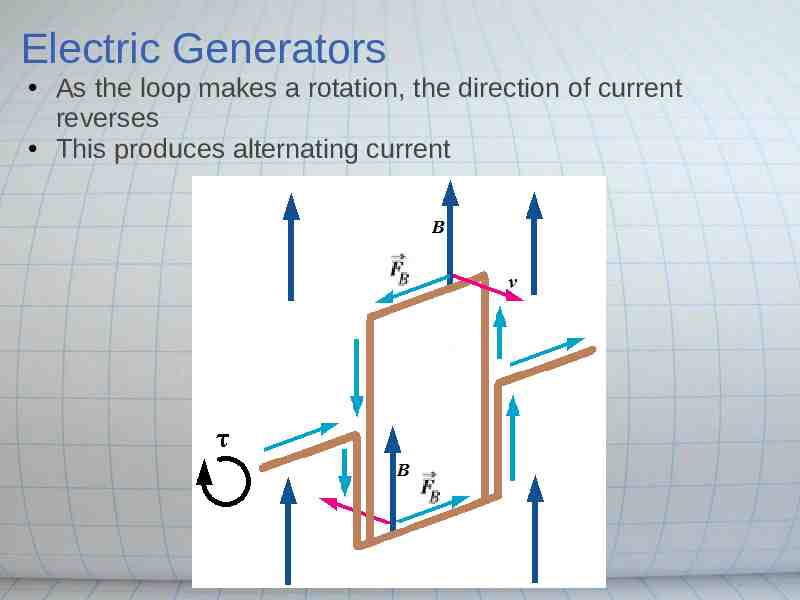
Electric Generators As the loop makes a rotation, the direction of current reverses This produces alternating current

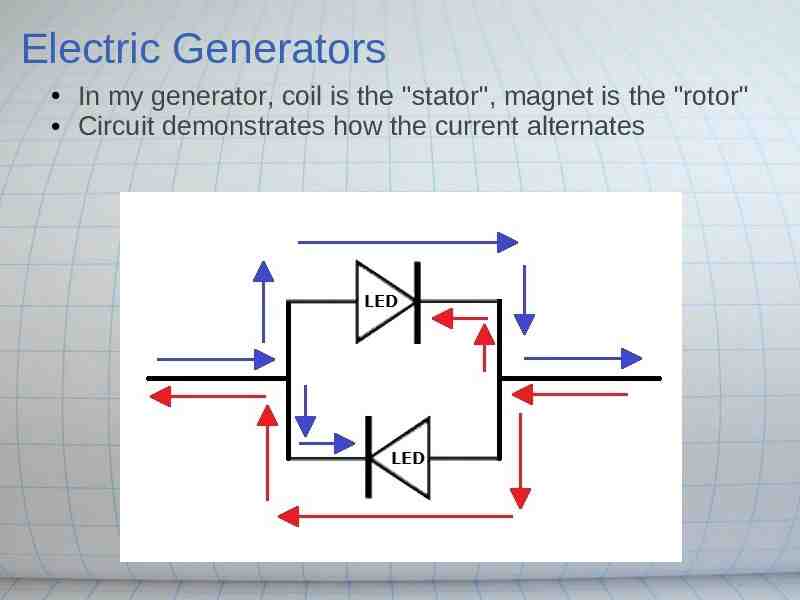
Electric Generators In my generator, coil is the "stator", magnet is the "rotor" Circuit demonstrates how the current alternates

Motors and Generators Different designs: magnet can be either rotor or stator Some motors use an electromagnet instead of a permanent magnet All designs operate on the same principle described here Charges moving relative to a magnetic field are pushed perpendicular to their motion and the field

Back-EMF and Symmetry Motors and generators are basically the same In some cases, a single device is used as both a motor and a generator Gas turbines, hybrid electric cars (regenerative breaking) This symmetry is important for a deeper reason.

Back-EMF and Symmetry Guarantees conservation of energy Current through a motor's coil causes it to rotate A rotating coil in a magnetic field induces voltage! By the Right-Hand Rule, this voltage is always in the opposite direction as the supplied voltage This is called back-EMF (ElectroMotive Force)

Back-EMF and Symmetry Likewise, current induced in a generator induces torque Torque opposes rotation of the generator These reaction forces always resist the applied forces This is required by the Maxwell-Faraday Equation:

Back-EMF and Symmetry Back-EMF is how energy is extracted from a voltage source by a motor Without load, motor is allowed to accelerate Back-EMF increases with motor speed When back-EMF equals supplied voltage, there is no net voltage, no current over the motor - it stops accelerating Since no current flows, no energy leaves the battery

Back-EMF and Symmetry Load on the motor extracts rotational energy Motor does not reach the same top speed, so back-EMF is always less than supply voltage Heavier load lower top speed more current flows

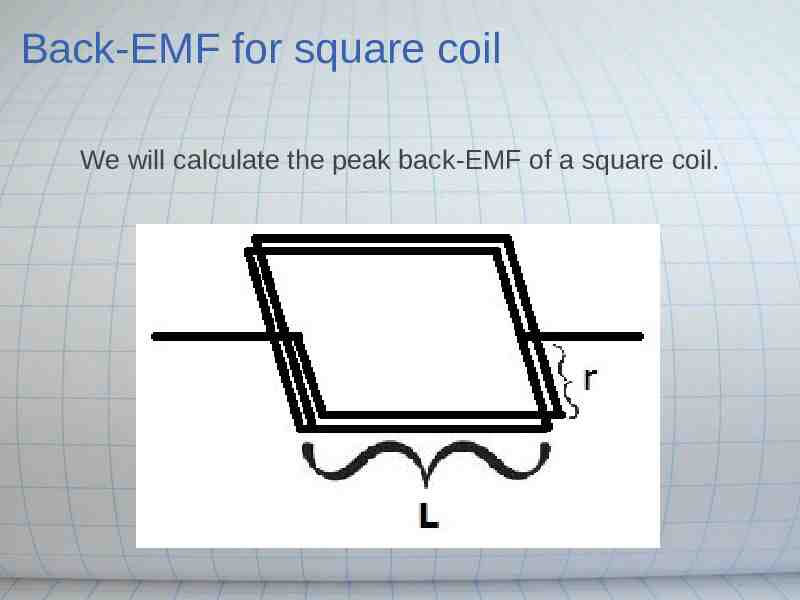
Back-EMF for square coil We will calculate the peak back-EMF of a square coil.

Back-EMF for square coil Assume B and v are perpendicular: Force on charge: FB qvB (v and B are perp.: drop sin(ϴ)) Force per unit charge: FB/q vB Work per unit charge over distance L: LFB/q LvB This is the Back-EMF over a distance L

Back-EMF for square coil Over the top and bottom edges of square coil: ϴ 90 degrees, sin(90) 1 Speed of edge v 2π*f*r 2π*f*0.019 m 6 turns, so length L 6*0.038 m B 0 T over top edge, 0.083 T over bottom edge 6*2π*f*(0.019 m)*(0.038 m)*(0.083 T) (0.0023 m2T)*f (0.0023 m2T)*f Vback

Back-EMF for square coil What about the 3 turn coil? 3*2π*f*(0.019 m)*(0.038 m)*(0.083 T) (0.0012 m2T)*f Vback At maximum speed, Vback should be equal for both coils So 6*2πfrLB 6*2πfrLB 2f1 f2 Top speed of the 3 turn coil should be about twice that of the 6 turn coil. Is it?

Other coils What about the rectangular coils? Circular coils? Will they be faster or slower? For rectangular coil, B 0.047 T (0.0013 m2T)*f Vback For circular coil, B 0.140 T (0.0039 m2T)*f Vback

Efficiency Vin 2.7 V, but only applied half the time, so 1.35 V These frequencies are much lower than we'd expect These motors have very low efficiencies Efficiency is defined in terms of power, energy-per-time Efficiency n Pout/Pin: ratio of input power to output power

Efficiency Ideally, mechanical power of a motor equals electrical input power Electrical power of a generator equals mechanical input power In reality, this never happens

Sources of Inefficiency Friction between the rotor and its joint Resistance and between electrons and the wire (resistance) Geometry - magnetic field, coil shapes don't maximize torque on coil

Design considerations Number of turns: more turns give more torque, but also more resistance Joints: sliding contacts have a lot of friction - some motors apply current to loop by induction Geometry: vast variation in designs to maximize magnetic force! o Iron cores in coils o Multiple coils, multiple magnets

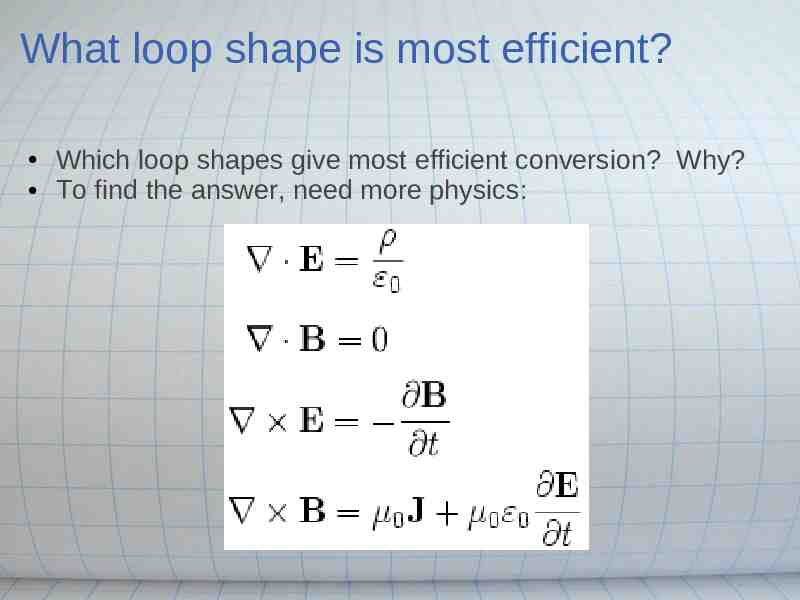
What loop shape is most efficient? Which loop shapes give most efficient conversion? Why? To find the answer, need more physics: