EE369 POWER SYSTEM ANALYSIS Lecture 3 Three Phase, Power

EE369 POWER SYSTEM ANALYSIS Lecture 3 Three Phase, Power System Operation Tom Overbye and Ross Baldick 1

Reading and Homework For lecture 3 read Chapters 1 and 2 For lectures 4 through 6 read Chapter 4 – we will not be covering sections 4.7, 4.11, and 4.12 in detail, – We will return to chapter 3 later. HW 3 is Problems 2.43, 2.45, 2.46, 2.47, 2.49, 2.50, 2.51, 2.52, 4.2, 4.3, 4.5, 4.7 and Chapter 4 case study questions A through D; due Thursday 9/15. 2

Per Phase Analysis Per phase analysis allows analysis of balanced 3 systems with the same effort as for a single phase system. Balanced 3 Theorem: For a balanced 3 system with: – All loads and sources Y connected, – No mutual Inductance between phases. 3

Per Phase Analysis, cont’d Then – All neutrals are at the same potential, – All phases are COMPLETELY decoupled, – All system values are the same “sequence” as sources. That is, peaks of phases occur in the same order. The sequence order we’ve been using (phase b lags phase a and phase c lags phase b) is known as “positive” sequence; in EE368L we’ll discuss “negative” and “zero” sequence systems. 4

Per Phase Analysis Procedure To do per phase analysis 1. Convert all load/sources to equivalent Y’s. 2. Solve phase “a” independent of the other phases 3. Total system power S 3 Va Ia* 4. If desired, phase “b” and “c” values can be determined by inspection (i.e., 120 degree phase shifts) 5. If necessary, go back to original circuit to determine line-line values or internal values. 5

Per Phase Example Assume a 3 , Y-connected generator with Van 1 0 volts supplies a -connected load with Z -j through a transmission line with impedance of j0.1 per phase. The load is also connected to a -connected generator with Va’’b’’ 1 0 through a second transmission line which also has an impedance of j0.1 per phase. Find 1. The load voltage Va’b’ 2. The total power supplied by each generator, SY and S 6

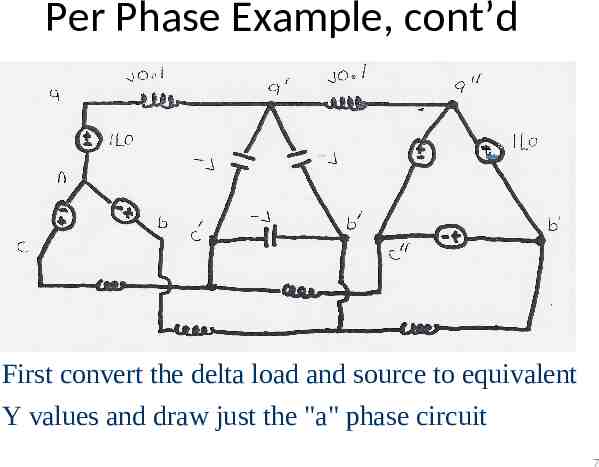
Per Phase Example, cont’d - First convert the delta load and source to equivalent Y values and draw just the "a" phase circuit 7

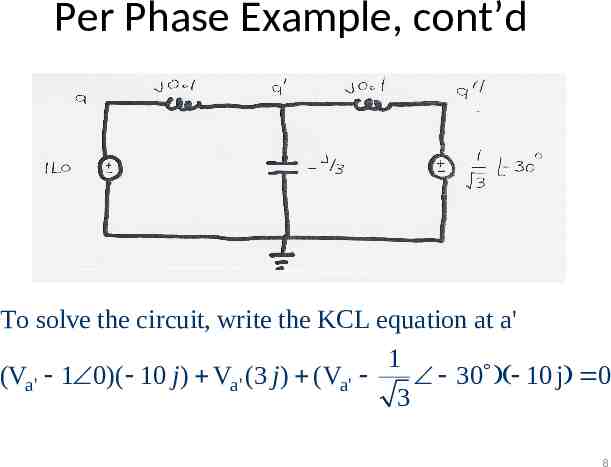
Per Phase Example, cont’d To solve the circuit, write the KCL equation at a' 1 (Va' 1 0)( 10 j ) Va' (3 j ) (Va' j 3 8

Per Phase Example, cont’d To solve the circuit, write the KCL equation at a' 1 (Va' 1 0)( 10 j ) Va' (3 j ) (Va' j 3 10 (10 j 60 ) Va' (10 j 3 j 10 j ) 3 Va' 0.9 volts Vc' 0.9 volts Vb' 0.9 volts Va'b' 1.56 volts 9

Per Phase Example, cont’d * Sygen 3Va I a* Va Va ' Va 5.1 j 3.5 VA j 0.1 * S gen Va '' Va ' 3Va '' 5.1 j 4.7 VA j 0.1 What is real power into load? Is this a reasonable dispatch of generators? What is causing real power flow from Y-connected generator to -connected generator? 10

Power System Operations Overview Goal is to provide an intuitive feel for power system operation Emphasis will be on the impact of the transmission system Introduce basic power flow concepts through small system examples 11

Power System Basics All power systems have three major components: Generation, Load and Transmission/Distribution. Generation: Creates electric power. Load: Consumes electric power. Transmission/Distribution: Moves electric power from generation to load. – Lines/transformers operating at voltages above 100 kV are usually called the transmission system. The transmission system is usually networked. – Lines/transformers operating at voltages below 100 kV are usually called the distribution system. The distribution system is usually radial except in urban 12 areas.

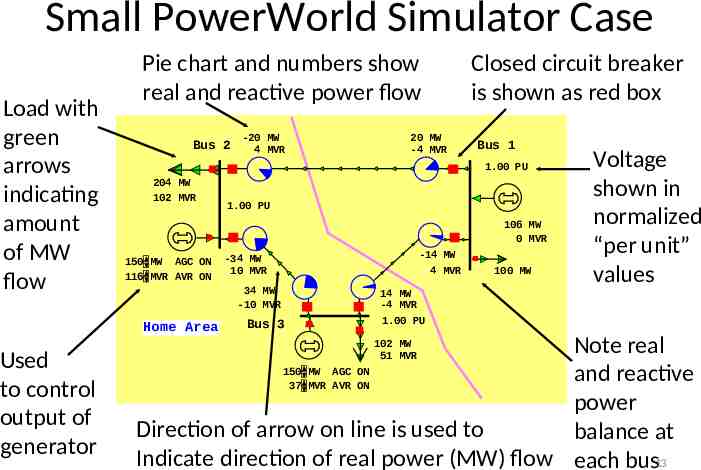
Small PowerWorld Simulator Case Load with green arrows indicating amount of MW flow Pie chart and numbers show real and reactive power flow Bus 2 20 MW -4 MVR Bus 1 1.00 PU 204 MW 102 MVR 1.00 PU 106 MW 0 MVR 150 MW AGC ON 116 MVR AVR ON -14 MW 4 MVR -34 MW 10 MVR 34 MW -10 MVR Home Area Used to control output of generator -20 MW 4 MVR Closed circuit breaker is shown as red box Bus 3 100 MW Voltage shown in normalized “per unit” values 14 MW -4 MVR 1.00 PU Note real 150 MW AGC ON and reactive 37 MVR AVR ON power Direction of arrow on line is used to balance at Indicate direction of real power (MW) flow each bus13 102 MW 51 MVR

Power Balance Constraints Power flow refers to how the power is moving through the system. At all times in the simulation the total power flowing into any bus MUST be zero! This is due to Kirchhoff’s current law. It can not be repealed or modified! Power is lost in the transmission system: If losses are small, the sending and receiving end power may appear the same when shown to two significant figures. 14

Basic Power Control Opening a circuit breaker causes the power flow to (nearly) instantaneously change. Other ways to directly control power flow in an AC transmission line require either power electronics, or transformers, or both: See “phase shifting transformers” in lecture 10. By changing generation (or, in principle, by changing load) we can indirectly change this flow. 15

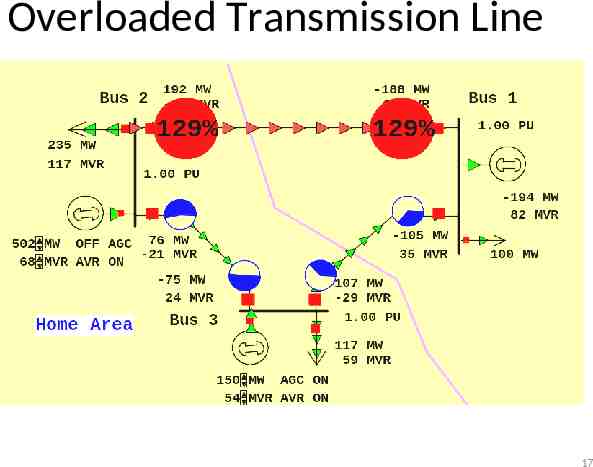
Transmission Line Limits Power flow in transmission line is limited by heating considerations. Losses (I2 R) heat up the line, causing it to sag. Each line has a limit: Simulator does not allow you to continually exceed this limit. Many transmission owners use winter/summer limits. Some transmission owners, eg Oncor, are moving to “dynamic” ratings that consider temperature etc. 16

Overloaded Transmission Line 17