ECE 616 Advanced FPGA Designs Electrical and Computer Engineering

ECE 616 Advanced FPGA Designs Electrical and Computer Engineering University of Western Ontario

General 1. Welcome remark 2. Digital and analog 3. VLSI: ASIC and FPGA 4. Overview 04/14/23 2

Course Requirement 1. Rules 1. Attendance 2. Projects: 3. Final 04/14/23 3

Information 1. Text book in library: M. J. S. Smith, Application-Specific Integrated Circuits, Addison-Wesley, 1997. ISBN: 0201500221. Digital Systems Design Using VHDL, Charles H. Roth, Jr., PWS Publishing, 1998 (ISBN: 0-534-95099-X). 2. Class notes and lab manual: www.engga.uwo.ca/people/wwang 04/14/23 4

Wei Wang Office: EC 1006 Office hours: Thursday 3:00 to 5:00 pm Email: 04/14/23 [email protected] 5

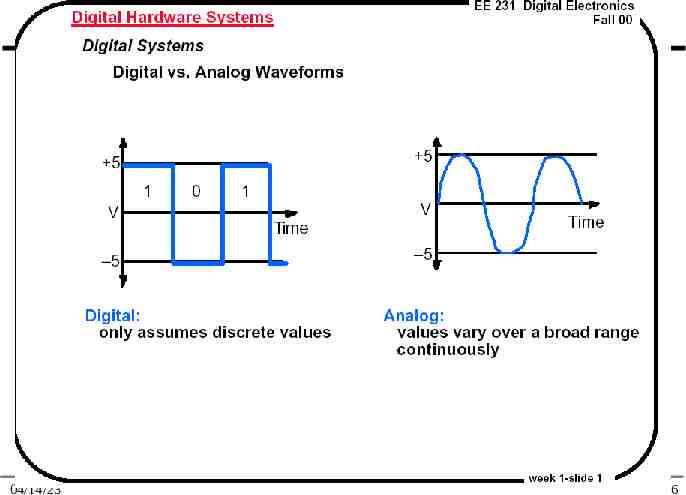
Digital and Analog 04/14/23 6

04/14/23 7

04/14/23 8

Overview Digital system: 489 materials VHDL FPGA and CPLD 04/14/23 9

Outline Review of Logic Design Fundamentals Combinational Logic Boolean Algebra and Algebraic Simplifications Karnaugh Maps 04/14/23 10

Combinational Logic Has no memory present state depends only on the present input x1 x2 xn X x1 x2. xn Z z1 z2. zm z1 z2 Z( t) F( X( t)) zm Note: Positive Logic – low voltage corresponds to a logic 0, high voltage to a logic 1 Negative Logic – low voltage corresponds to a logic 1, high voltage to a logic 0 04/14/23 11

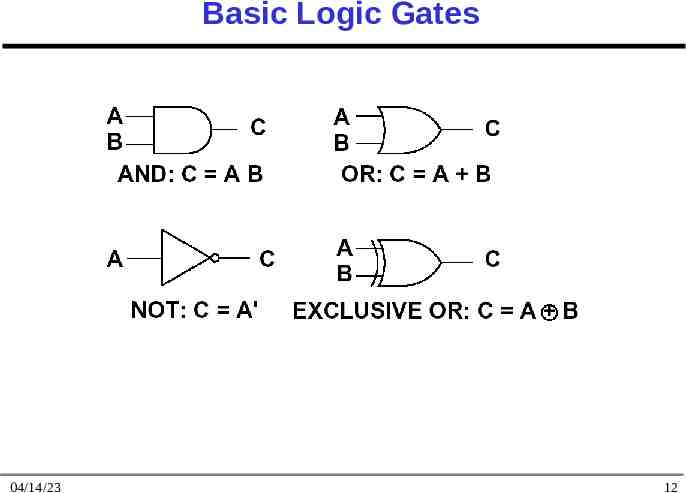
Basic Logic Gates 04/14/23 12

Full Adder Module Truth table Algebraic expressions F(inputs for which the Minterms function is 1): Sum X' Y' Cin X' YCin' XY' Cin' XYCin Cout X' YCin XY' Cin XYCin' XYCin m-notation Sum m1 m2 m4 m7 m(1, 2, 4, 7) Cout m3 m5 m6 m7 m(3, 5, 6, 7) 04/14/23 13

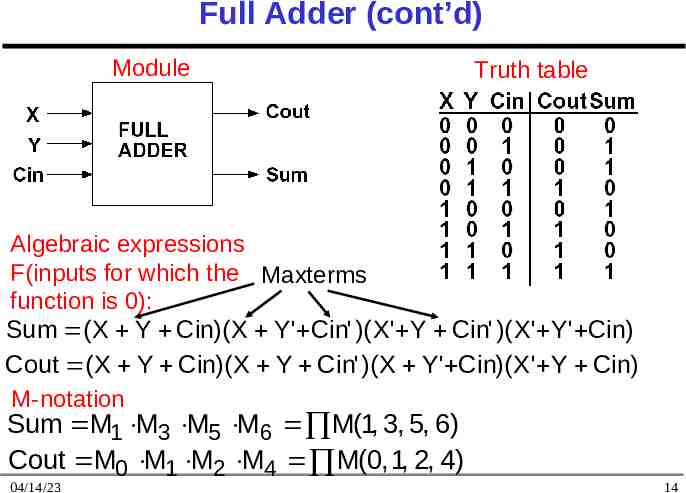
Full Adder (cont’d) Module Truth table Algebraic expressions F(inputs for which the Maxterms function is 0): Sum ( X Y Cin)( X Y' Cin' )( X' Y Cin' )( X' Y' Cin) Cout ( X Y Cin)( X Y Cin' )( X Y' Cin)( X' Y Cin) M-notation Sum M1 M3 M5 M6 M(1, 3, 5, 6) Cout M0 M1 M2 M4 M(0, 1, 2, 4) 04/14/23 14

Boolean Algebra Basic mathematics used for logic design Laws and theorems can be used to simplify logic functions – Why do we want to simplify logic functions? 04/14/23 15

Laws and Theorems of Boolean Algebra 04/14/23 16

Laws and Theorems of Boolean Algebra 04/14/23 17

Simplifying Logic Expressions Combining terms – Use XY XY’ X, X X X Cout X' YCin XY' Cin XYCin' XYCin ( X' YCin XYCin) ( XY' Cin XYCin) ( XYCin' XYCin) YCin XCin XY Eliminating terms – Use X XY X Eliminating literals – Use X X’Y X Y Adding redundant terms – Add 0: XX’ – Multiply with 1: (X X’) 04/14/23 18

Theorems to Apply to Exclusive-OR X 0 X X 1 X' X X 0 X X' 1 X Y Y X (Commutative law) ( X Y) Z X ( Y Z) (Associative law) X( Y Z) XY XZ (Distributive law) ( X Y)' X Y' X' Y XY X' Y' 04/14/23 19

Karnaugh Maps Convenient way to simplify logic functions of 3, 4, 5, (6) variables Four-variable K-map Location of minterms – each square corresponds to one of the 16 possible minterms – 1 - minterm is present; 0 (or blank) – minterm is absent; – X – don’t care the input can never occur, or the input occurs but the output is not specified – adjacent cells differ in only one value can be combined 04/14/23 20

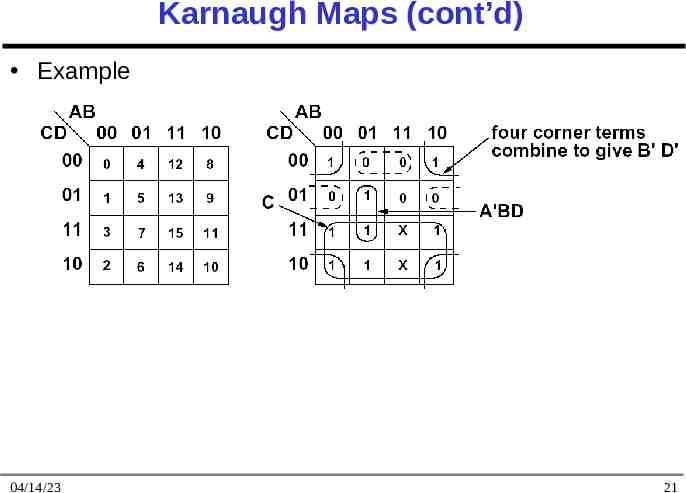
Karnaugh Maps (cont’d) Example 04/14/23 21

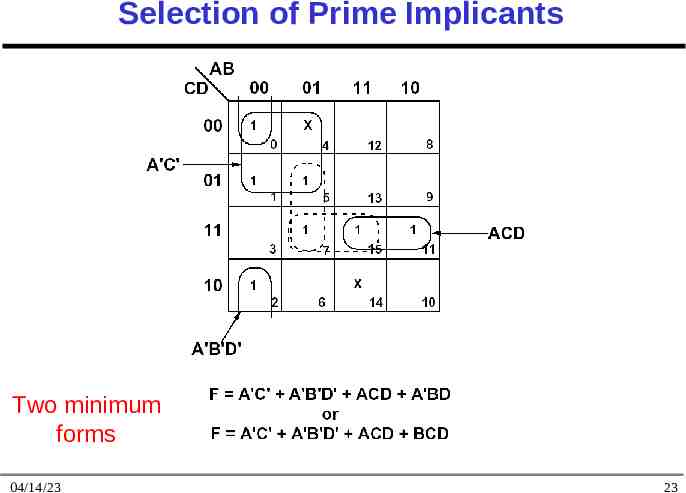
Sum-of-products Representation Function consists of a sum of prime implicants Prime implicant – a group of one, two, four, eight 1s on a map represents a prime implicant if it cannot be combined with another group of 1s to eliminate a variable Prime implicant is essential if it contains a 1 that is not contained in any other prime implicant 04/14/23 22

Selection of Prime Implicants Two minimum forms 04/14/23 23

Procedure for min Sum of products 1. Choose a minterm (a 1) that has not been covered yet 2. Find all 1s and Xs adjacent to that minterm 3. If a single term covers the minterm and all adjacent 1s and Xs, then that term is an essential prime implicant, so select that term 4. Repeat steps 1, 2, 3 until all essential prime implicants have been chosen 5. Find a minimum set of prime implicants that cover the remaining 1s on the map. If there is more than one such set, choose a set with a minimum number of literals 04/14/23 24

Products of Sums F(1) {0, 2, 3, 5, 6, 7, 8, 10, 11} F(X) {14, 15} 04/14/23 25

To Do Textbook – Chapter 1.1, 1.2 Read – Altera’s MAX plus II and the UP1 Educational board: A User’s Guide, B. E. Wells, S. M. Loo – Altera University Program Design Laboratory Package 04/14/23 26