EC500 E1: Parallel Programming and HPC Parallelizing 2D Convolutions

EC500 E1: Parallel Programming and HPC Parallelizing 2D Convolutions on GPUs Group 1: Michael Clifford, Patrick Dillon, Frank Tranghese

Outline Introduction - What Is a Convolution and Why is it important Work Planned vs Work Accomplished Parallelization Strategy Results Road Blocks Time Complexity Memory Issues Lessons Learned Next Steps Conclusion

Goal The goal of our project is to work with 2D convolution, a widely-used and simple, yet computationally inefficient algorithm, and explore methods to speed it up by implementing parallelization with GPU’s

What is a Convolution? A 1D convolution is a linear combination of two functions: f, some signal that you have recorded and g, a filter to process the signal data in some desired fashion (i.e. smoothing, edge detection, or lowpass). You can extend the convolution into 2, 3, N dimension. Convolution is a common data processing method that is used in a wide variety of domains. The 2D convolution has a worst case time complexity of O(n4). So finding methods to improve performance is key. Image from Wikipedia

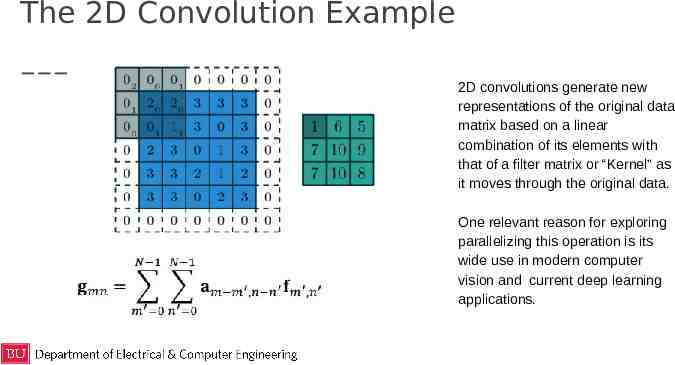
The 2D Convolution Example 2D convolutions generate new representations of the original data matrix based on a linear combination of its elements with that of a filter matrix or “Kernel” as it moves through the original data. One relevant reason for exploring parallelizing this operation is its wide use in modern computer vision and current deep learning applications.

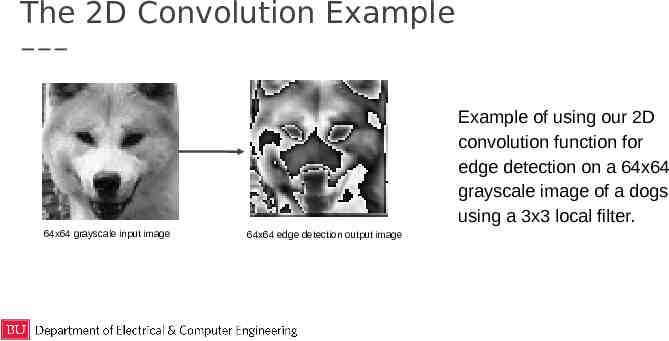
The 2D Convolution Example Example of using our 2D convolution function for edge detection on a 64x64 grayscale image of a dogs using a 3x3 local filter. 64x64 grayscale input image 64x64 edge detection output image

Work Planned vs Work Accomplished Build the 2D convolution function, FFT and the resulting matrices in both serial and parallel fashion Building the 2D convolution matrix follows a specific pattern and can be parallelized Reshaping the image, performing matrix math, and reshaping back to original size are all also parallelizable operations. Compare direct convolution to FFT2 Parallelize FFT Test both parallelized methods and compare/contrast for different inputs (different sized images and kernels) Use OpenACC for GPU parallelization Use OpenACC on the SCC

Work Planned vs Work Accomplished Built 2D convolution functions in C Built Circulant Matrix Variant Built Direct Variant Built 2D FFT method for comparison Used built-in image libraries for reading images Built function to generate 2D black and white noise images to test scaling Parallelized code for Direct Variant Compared direct variant with multiple compiling methods on SCC Serial, Multicore CPU and GPU Required porting much of the code from C to C. Used OpenACC for GPU and parallelization Use OpenACC on the SCC

Parallelization Strategy Initial strategy looked to parallelize each helper function required to perform the entire convolution as well as the convolution function itself Generating the Circulant Matrix Converting 2D matrices into 1D Vectors Generating Images and Filters to Convolve The main convolution function

Parallelization Strategy The convolution operation is highly parallelizable due to each step in the algorithm being independent of the rest. Each KxK block can be computed correctly without information from any of the others. Our plan was to compute all KxK blocks simultaneously using the openACC library

Parallelization Strategy

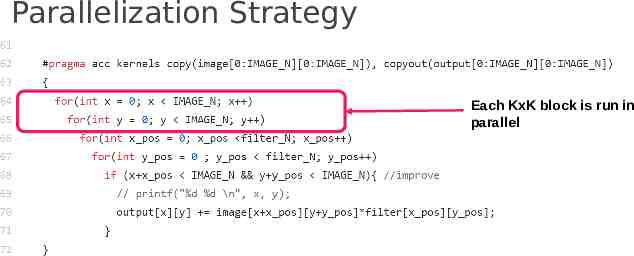
Parallelization Strategy Each KxK block is run in parallel

Parallelization with OpenACC pgcc -DUSE DOUBLE -Minfo accel -fast -acc -ta tesla:cc20 -c main.c -g main: 62, Generating implicit copyin(filter[:][:]) Generating copyout(output[:][:]) Generating copy(image[:][:]) 64, Loop is parallelizable 65, Loop is parallelizable 66, Loop carried dependence of output prevents parallelization Loop carried backward dependence of output prevents vectorization 67, Complex loop carried dependence of output prevents parallelization Loop carried dependence of output prevents parallelization Loop carried backward dependence of output prevents vectorization Inner sequential loop scheduled on accelerator Accelerator kernel generated Generating Tesla code 64, #pragma acc loop gang /* blockIdx.y */ 65, #pragma acc loop gang, vector(128) /* blockIdx.x threadIdx.x */ 66, #pragma acc loop seq 67, #pragma acc loop seq

Results Parallel Code is Faster Than Serial Code! But how much faster, and in what cases? We ran the following 3 Experiments: 3x3 kernel on grayscale images ranging from 16x16 to 16384x16384 16x16 kernel on grayscale images ranging from 16 x16 to 16384x16384 All-to-All kernel on grayscale images ranging from 16x16 to 1024x1024 We compared the performance of serial code run on a CPU, parallelized multicore CPU and parallelized GPU. All were run in an interactive session on the SCC with 1 GPU.

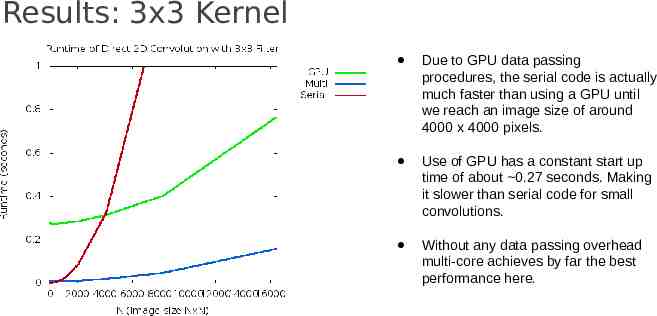
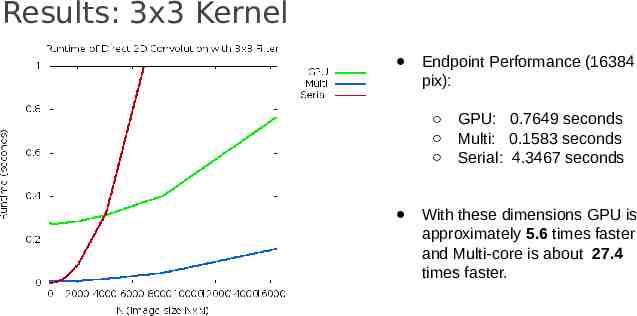
Results: 3x3 Kernel Due to GPU data passing procedures, the serial code is actually much faster than using a GPU until we reach an image size of around 4000 x 4000 pixels. Use of GPU has a constant start up time of about 0.27 seconds. Making it slower than serial code for small convolutions. Without any data passing overhead multi-core achieves by far the best performance here.

Results: 3x3 Kernel Endpoint Performance (16384 pix): GPU: 0.7649 seconds Multi: 0.1583 seconds Serial: 4.3467 seconds With these dimensions GPU is approximately 5.6 times faster and Multi-core is about 27.4 times faster.

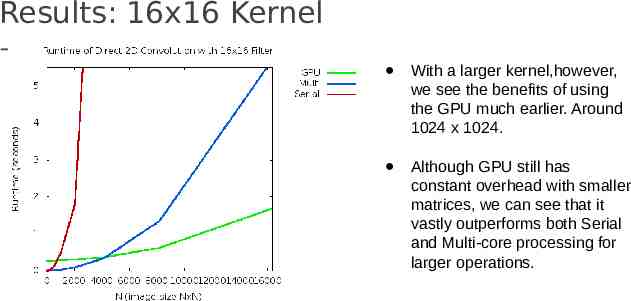
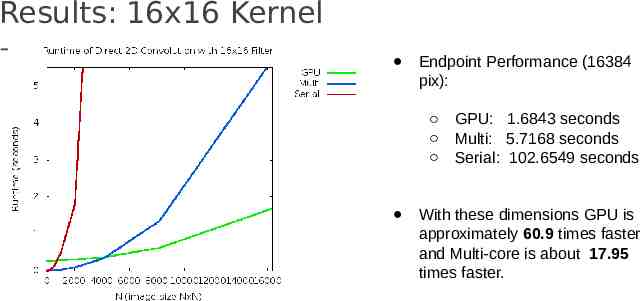
Results: 16x16 Kernel With a larger kernel,however, we see the benefits of using the GPU much earlier. Around 1024 x 1024. Although GPU still has constant overhead with smaller matrices, we can see that it vastly outperforms both Serial and Multi-core processing for larger operations.

Results: 16x16 Kernel Endpoint Performance (16384 pix): GPU: 1.6843 seconds Multi: 5.7168 seconds Serial: 102.6549 seconds With these dimensions GPU is approximately 60.9 times faster and Multi-core is about 17.95 times faster.

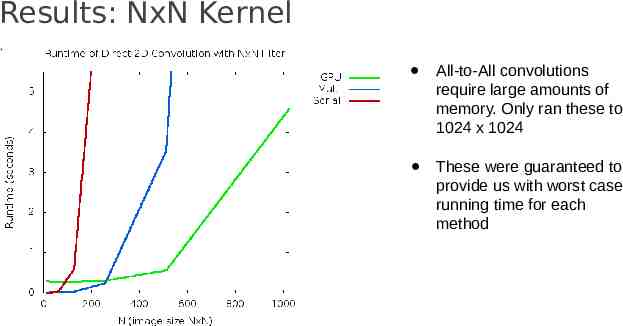
Results: NxN Kernel All-to-All convolutions require large amounts of memory. Only ran these to 1024 x 1024 These were guaranteed to provide us with worst case running time for each method

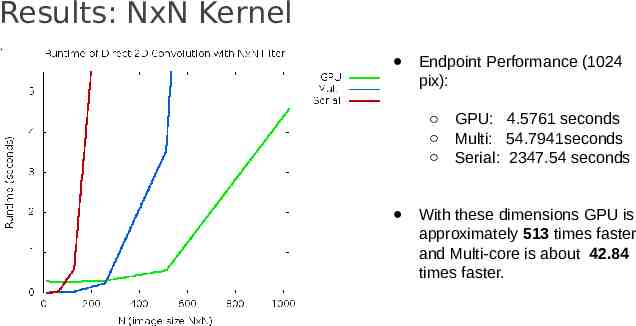
Results: NxN Kernel Endpoint Performance (1024 pix): GPU: 4.5761 seconds Multi: 54.7941seconds Serial: 2347.54 seconds With these dimensions GPU is approximately 513 times faster and Multi-core is about 42.84 times faster.

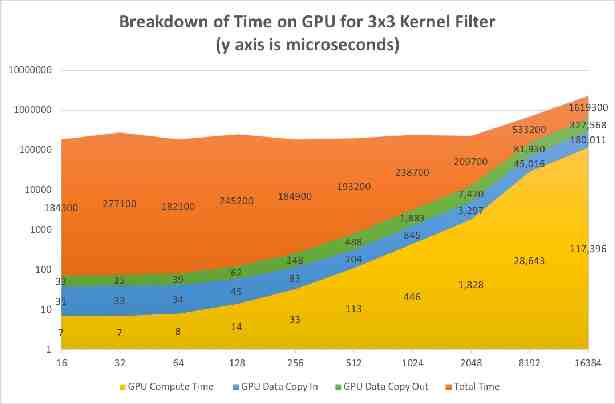
A Closer Look at GPU Timing Set the PGI ACC TIME environment variable to receive detailed timing info regarding GPU: Accelerator Kernel Timing data main NVIDIA devicenum 0 time(us): 625,121 62: compute region reached 1 time 67: kernel launched 1 time grid: [128x256] block: [128] device time(us): total 117,676 max 117,676 min 117,676 avg 117,676 elapsed time(us): total 117,736 max 117,736 min 117,736 avg 117,736 62: data region reached 4 times 62: data copyin transfers: 65 device time(us): total 179,962 max 2,820 min 8 avg 2,768 81: data copyout transfers: 130 device time(us): total 327,483 max 2,605 min 25 avg 2,519

Road Blocks: PGCC compiler on SCC Initial code was in C and used the CImg library Unfortunately could not compile on PGCC PGCC has dependence on GCC and referenced GCC 4.4. Attempted fixes: Switching between Evan’s PGCC install and SCC install Changing localrc files to point to newer version We gave up on getting existing code and rewrote Removed any dependencies for GCC 4.4 in both a C and a C version

Road Blocks: PGCC compiler on SCC In C we had to remove image library. Attempted hacks: Separating into different files and using different compilers Compiling as a library and linking This should be possible, but became a distraction C we used lodepng library but abandoned it because of difficulty debugging Went with C version because it was easier to locate parallelization

Road Blocks: Memory Issues Memory Issues: Initial circular convolution method required massive memory overhead to store secondary matrices. Memory needs became untenable at around 512 x 512 pixel images. At this point we switched to the direct convolution method. Despite modified approach, unless a reasonably sized local kernel was used, memory issues remained.

Lessons Learned In real-world applications, memory bandwidth can be as important (if not more so) than computational complexity. We quickly ran into memory allocation issues that we had not originally considered when focusing solely on parallelizing the computations. OpenACC is an extremely powerful tool that can generate orders of magnitude speedups with a single line of code.

Future Work Parallelize FFT and compare performance on similar tests. Implement image reading function and use more interesting filters Create matrices on GPU to minimize data movement (this would only work for certain kinds of matrices--not images)

Conclusion GPU’s can be expensive to initialize and so provide little benefit on smaller tasks. However the economy of scale quickly becomes realized (1024 x 1024 convolution runs over 500x faster than serial variant!) OpenACC is amazing (once you get it working) Despite GPU’s massive speed up at larger scales, more work is needed to intelligently manage data allocation and movement.

THANKS!