Dynamic Spectrum Management: Optimization, game and equilibrium

Dynamic Spectrum Management: Optimization, game and equilibrium Tom Luo (Yinyu Ye) December 18, WINE 2008

Outline Introduction of Dynamic Spectrum Management (DSM) Social Utility Optimization Noncooperative Nash Game Competitive Spectrum Economy Pure exchange market Budget Allocation Channel Power Production The objective is to apply algorithmic game/equilibrium theory to solving real and challenging problems

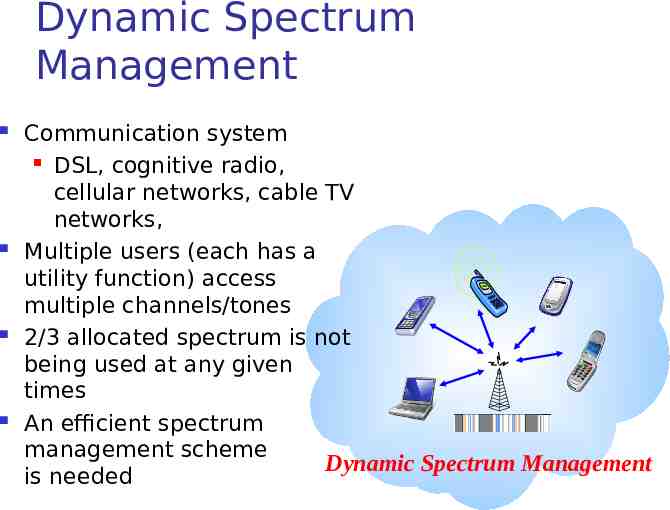
Dynamic Spectrum Management Communication system DSL, cognitive radio, cellular networks, cable TV networks, Multiple users (each has a utility function) access multiple channels/tones 2/3 allocated spectrum is not being used at any given times An efficient spectrum management scheme Dynamic Spectrum Management is needed

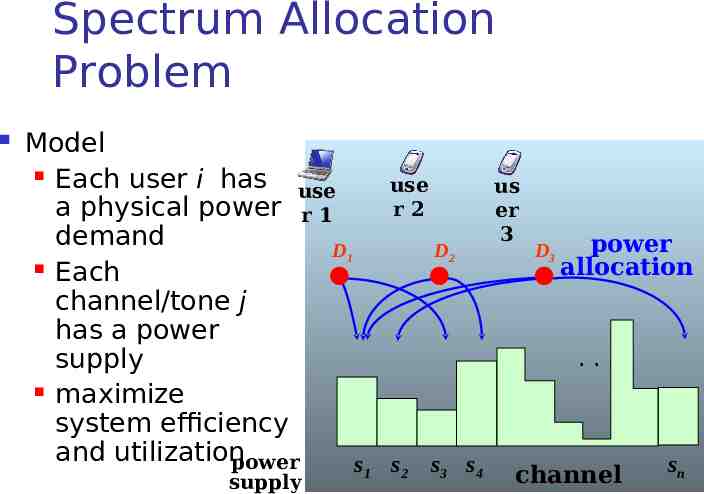
Spectrum Allocation Problem Model Each user i has use a physical power r 1 demand D1 Each channel/tone j has a power supply maximize system efficiency and utilization power s supply use r2 D2 us er 3 D3 power allocation . 1 s2 s3 s4 channel sn

Shannon Utility Function ui ( xi , xi ) log(1 j xij i kj kj ij a x ) k i xij: the power allocation to user i on channel j x-bari: power allocations to all users other than i бij: the crosstalk ratio to user i on channel j aikj: the interference ratio from user k on channel j They may time varying and stochastic

Spectrum Management Models From the optimization perspective, the dynamic spectrum management problem can be formulated as 1. Social utility maximization 2. Noncooperative Nash game May not optimize individual utilities simultaneously Generally hard to achieve May not achieve social economic efficiency 3. Competitive economy market Price mechanism proposed to achieve social economic efficiency and individual optimality

1. Social Utility Maximization Maximize i Subject to u (x , x ) i i i x ij j x ij d , i i s j , j i where x represents the power on ij channel j alloacated to user i.

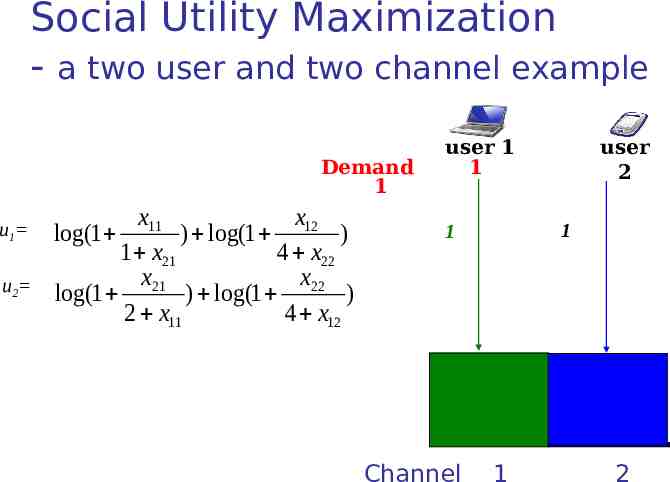
Social Utility Maximization - a two user and two channel example Demand 1 u1 u2 x11 x12 log(1 ) log(1 ) 1 x21 4 x22 x21 x22 log(1 ) log(1 ) 2 x11 4 x12 user 1 1 1 1 Channel user 2 1 2

Difficulty of the problem Even in the two user case, the problem is NP-hard. No constant approximation algorithm even for one channel and multiple users. Problems under the Frequency Division Multiple Access (FMDA) policy can be solved efficiently Luo and Zhang 2007

2. Noncooperative Nash Game Model Each user maximize its own utility under a physical power demand constraint Ciofi and Yu 2002, etc. use r1 use r2 D1 D2 us er 3 D3 power allocation . chann el

Individual rationality Maximize Subject to u (x , x ) i i i T e x xij d , x 0; i i i j The basic game assumes that there is no limit on power supply for each channel. IWF: iterative water filling algorithm converges in certain cases

Spectrum Nash Game - the same toy example Demand 1 u 1 u2 x11 x12 log(1 ) log(1 ) 1 x21 4 x22 x21 x22 log(1 ) log(1 ) 2 x11 4 x12 user 1 1 1 1 Channel user 2 1 2

Results on the problem No bound on price of anarchy’’ Can be solved as finding solution of a linear complementarity problem, so that it’s PPAD hard in general There is a FPTAS under symmetric interference condition There is a polynomial time algorithm under symmetric and strong weak interference condition Key to the proofs: the LCP matrix is symmetric Luo and Pang 2006, Xie, Armbruster, and Y 2008

3. Competitive Spectrum Market The problem was first formulated by Leon Walras in 1874, and later studied by Arrow, Debreu, and Fisher, also see Brainard and Scarf. Agents are divided into two categories: seller and buyer. Buyers have a budget to buy goods and maximize their individual utility functions; sellers sell their goods just for money. An equilibrium is an assignment of prices to all goods, and an allocation of goods to every buyer such that it is maximal for the buyer under the given prices and the market clears.

Market Equilibrium Condition I Individual Rationality Given market prices p for all goods Maximize u (x , x ) i i i Subject to pT x w , x 0; i i i where x represents the amount of ij good j purchased by agent i and wi is its budget

Market Equilibrium Condition II Physical Constraint: The total purchase volume for good j should not exceed its available supply: x ij i s j , j ;

Market Equilibrium Condition III Walras Law: For good j x ij i s j , p j 0;

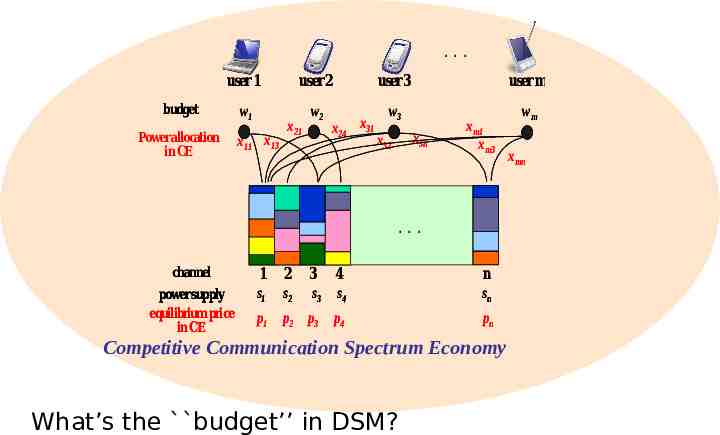
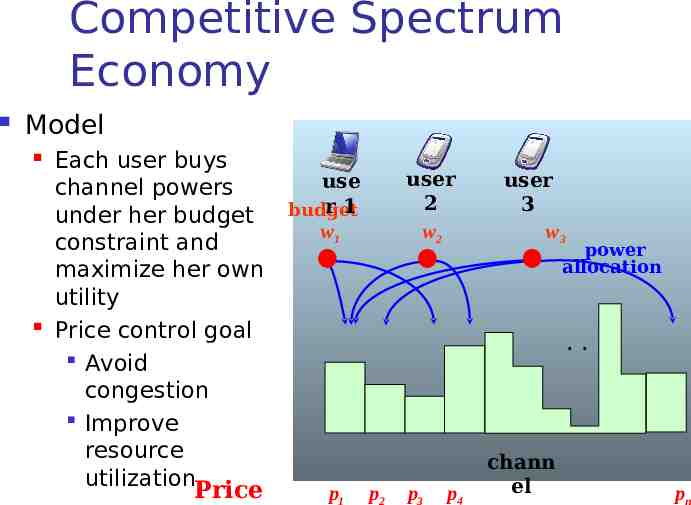
. user 1 user 2 w1 w2 budget Power allocation in CE x11 x13 x21 x24 user 3 x31 user m w3 x3n x32 xm1 xm3 wm wi 1 xmn . channel power supply equilibrium price in CE 1 s1 2 s2 3 4 s3 s4 n sn p1 p2 p3 p4 pn Competitive Communication Spectrum Economy What’s the budget’’ in DSM? sj m

3.1 Competitive Equilibrium in Spectrum Economy for Fixed Budget and Power Supply

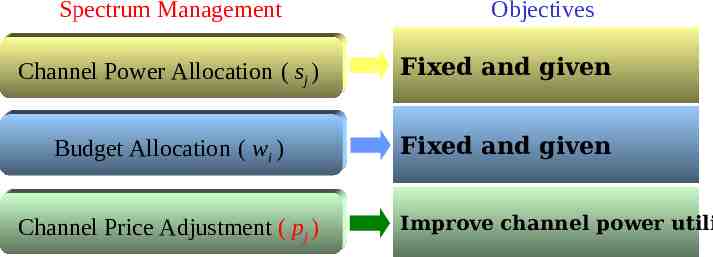
Spectrum Management Objectives Channel Power Allocation ( sj ) Fixed and given Budget Allocation ( wi ) Fixed and given Channel Price Adjustment ( pj ) Improve channel power utili

Competitive Spectrum Economy Model Each user buys channel powers under her budget constraint and maximize her own utility Price control goal Avoid congestion Improve resource utilization Price user 2 w2 use r1 budget w1 user 3 w3 power allocation . p1 p2 p3 p4 chann el pn

w1 x11 x13 Problem Formulation s1 x21 w2 x24 x31 w3 x32 xmn . s2 s3 s4 m users, each has a budget wi n channels, each with power capacity sj Design variable x3n wm xm4 sn xij Power allocation for i th user in jth channel pj Price for j th channel (Nash Equilibrium: pj 1 fixed) Ã ! User utility n (Shannon utility function ) X xi j P u(xi ; x ¹i) log 1 ; i 1; ; m: i ¾i j k6 i akj xkj j 1

Competitive Equilibrium Model Theorem A competitive equilibrium always exists for the spectrum management problem Y 2007 based on the Lemma of Abstract Economy developed by Debreu 1952

Equilibrium Properties Every channel has a price: p *j 0, j All power supply are allocated: m * x i 1 ij s j j. All budget are spent m n * w p i 1 i j 1 j s j

Weak-Interference Market Weak-interference environment: the Shannon utility function of user i is xij ui ( xi , xi ) log 1 ij aij ( xkj ) j 1 k i where ij 0, 0 aij 1 n In the weak-interference environment, An equilibrium can be computed in polynomial time. The competitive price equilibrium is unique. Moreover, if the crosstalk ratio is strictly less than 1, then the power allocation is also unique. (Y 2007)

Two methods of solving competitive equilibrium Centralized Solving the equilibrium conditions Decentralized Iterative price-adjusting

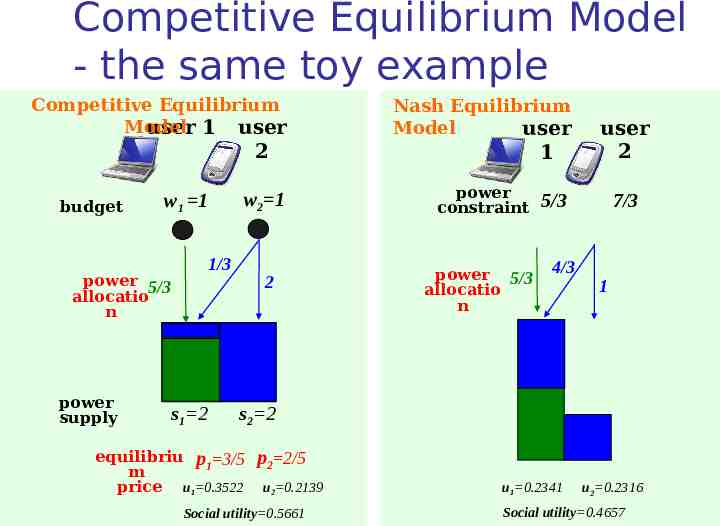
Competitive Equilibrium Model - the same toy example Competitive Equilibrium Model user 1 user 2 budget power 5/3 allocatio n power supply w2 1 w1 1 1/3 s1 2 2 Nash Equilibrium Model user 1 power constraint power 5/3 allocatio n user 2 7/3 5/3 4/3 1 s2 2 equilibriu p 3/5 1 m price u1 0.3522 p2 2/5 u2 0.2139 Social utility 0.5661 u1 0.2341 u2 0.2316 Social utility 0.4657

Computational Results Compare competitive equilibrium and Nash equilibrium Evaluate the performance in Individual utility and Social utility In most cases, CE results in a channel allocation Have a higher social utility value Make more users achieve higher individual utilities

3.2 Budget Allocation in Competitive Spectrum Economy

Spectrum Management Channel Power Allocation ( sj ) Objectives Fixed and given Budget Allocation ( wi ) Make each user meet minimu power demand or utility valu threshold Channel Price Adjustment ( pj ) Improve channel power utiliz Lin, Tasi, and Y 2008

Budget Allocation in Competitive Spectrum Economy Budget allocation aims to satisfy a minimum physical power demand di for each user i or satisfy a minimum utility value u for i each user i ; e.g., all users achieve an identical utility value Theorem: Such a budget equilibrium always exists.

Two methods of solving competitive equilibrium Centralized Solving entire optimal conditions which may be nonconvex Decentralized Iterative budget-adjusting

Budgeting for demand - computational results Number of (budget-adjusting) iterations required to achieve individual power demands

Budgeting for demand - computational results Number of iterations and CPU time (seconds) required to satisfy individual power demands in large scale problems, error tolerance 0.05

Budgeting for demand - CE and NE comparison results General cases: background noise randomly selected from (0,m], crosstalk ratio randomly selected from [0,1] In all cases, the social utility of CE is better than that of NE.

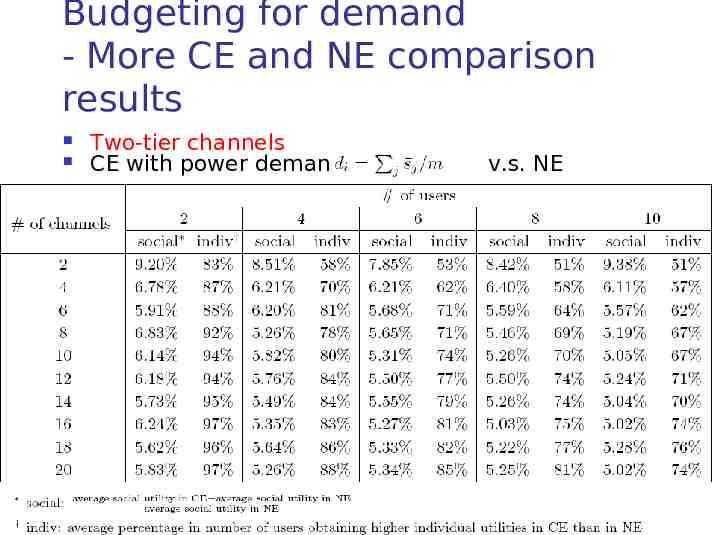
Budgeting for demand - More CE and NE comparison results In special type of problems, the competitive equilibrium performs much better than the Nash equilibrium does. For instance, the channels being divided into two categories: high-quality and lowquality. (In simulations, one half of channels with background noise randomly selected from the interval (0; 0,1] and the other half of channels with background noise randomly selected from the interval [1;m].)

Budgeting for demand - More CE and NE comparison results Two-tier channels CE with power demands v.s. NE

Budget allocation to balance utilities - Computational results Number of iterations and CPU time (seconds) required to balance individual utilities in large scale problems, difference tolerance 0.05

Budgeting to balance utilities - CE and NE comparison results Two-tier channels CE with balanced utilities v.s. NE

Comparison result summaries Compare with NE, in most cases, CE with minimum power demands results in power allocation Compare with NE, in most cases, CE with balanced utilities demands results in a power allocation Have a higher social utility Have a higher social utility Make more users have higher individual utilities Have a smaller gap between maximal individual utility and minimal individual utility In special type of problems, for instance, two tiers of channels, CE performs much better than NE does.

3.3 Channel Power Production in Competitive Spectrum Economy

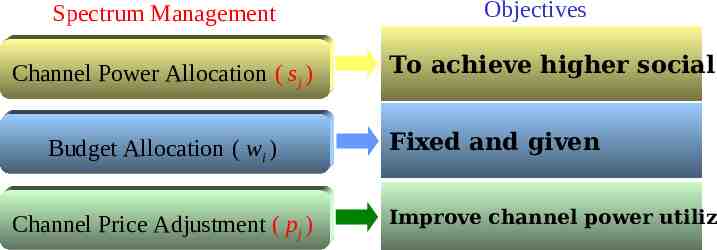
Spectrum Management Channel Power Allocation ( sj ) Budget Allocation ( wi ) Channel Price Adjustment ( pj ) Objectives To achieve higher social Fixed and given Improve channel power utiliz

Produce power supply to increase social utility: the same toy example u1 u2 x11 x12 log(1 ) log(1 ) 1 x21 4 x22 x21 x22 log(1 ) log(1 ) 2 x11 4 x12 w1 w2 1 s1 s2 4

social utility of CE social utility of NE (scale to used power in CE) 0.7 0.6 social utility 0.5 0.4 0.3 0.2 0.1 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4 the power supply of channel 1 (s1)

Future Work How to systematically adjust channel power supply capacity to increase social utility? The convergence of the iterative variable-adjusting method for general setting Real-time spectrum management vs optimal policy at top levels