DRA/K V Decision and Risk Analysis Financial Modelling & Risk Analysis

DRA/K V Decision and Risk Analysis Financial Modelling & Risk Analysis Kiriakos Vlahos Spring 2000

DRA/K V Session overview Why do we need risk analysis? Project evaluation Risk analysis approaches – Scenario analysis – Sensitivity analysis – Monte-Carlo simulation Summary

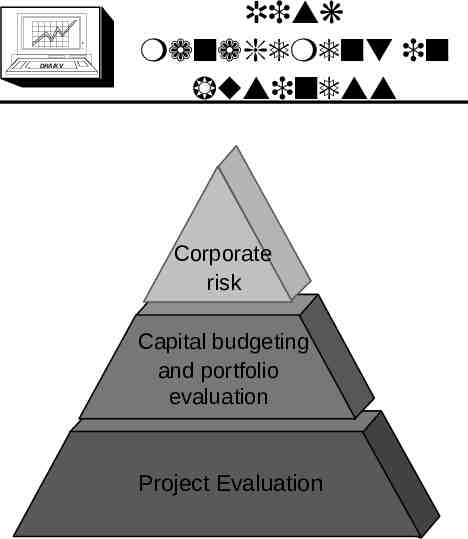
DRA/K V Risk management in business Corporate risk Capital budgeting and portfolio evaluation Project Evaluation

DRA/K V Why do we need risk analysis? Single point forecasts are dangerous! Derive bounds for the range of possible outcomes Sensitivity testing of the assumptions Better perception of risks and their interaction Anticipation and contingency planning Overall reduction of risk exposure through hedging Risk analysis helps you develop insights, knowledge and confidence for better decision making and risk management.

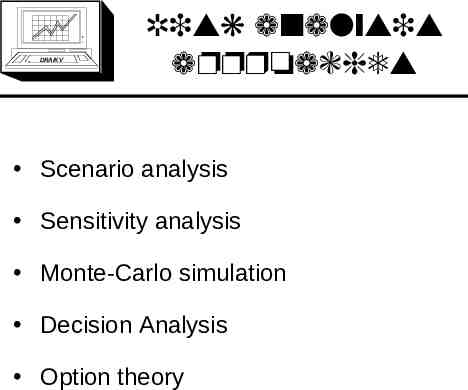
DRA/K V Risk analysis approaches Scenario analysis Sensitivity analysis Monte-Carlo simulation Decision Analysis Option theory

DRA/K V Skywalker Proposal to open and operate a video store. “You can expect to make at least 50,000 in the first year” Assumptions Monthly Purchase (no of tapes) Tape Price Tape Life (no of plays) Plays per Mth (per tape) Rent per Day Shop Rent p a Interest p a 50 30 30 4.33 3 6,000 10%

DRA/K V Project Evaluation Evaluating a business proposition – Does it make sense overall? Market conditions Trust issues – What is the outlook under a basic set of assumptions? (Base Case) – What are the risks involved? Writing a business plan

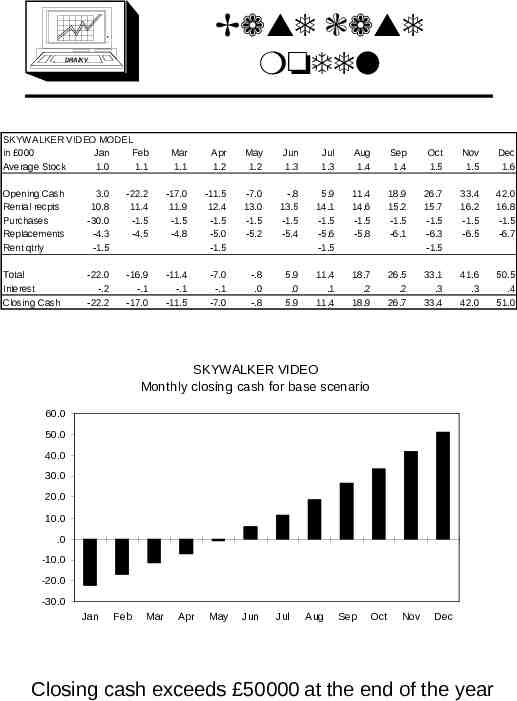
Base case model DRA/K V SKYWALKER VIDEO MODEL in 000 Jan Feb Average Stock 1.0 1.1 Mar 1.1 Apr 1.2 May 1.2 Jun 1.3 Jul 1.3 Aug 1.4 Sep 1.4 Oct 1.5 Nov 1.5 Dec 1.6 Opening Cash Rental recpts Purchases Replacements Rent qtrly 3.0 10.8 -30.0 -4.3 -1.5 -22.2 11.4 -1.5 -4.5 -17.0 11.9 -1.5 -4.8 -11.5 12.4 -1.5 -5.0 -1.5 -7.0 13.0 -1.5 -5.2 -.8 13.5 -1.5 -5.4 5.9 14.1 -1.5 -5.6 -1.5 11.4 14.6 -1.5 -5.8 18.9 15.2 -1.5 -6.1 26.7 15.7 -1.5 -6.3 -1.5 33.4 16.2 -1.5 -6.5 42.0 16.8 -1.5 -6.7 Total Interest Closing Cash -22.0 -.2 -22.2 -16.9 -.1 -17.0 -11.4 -.1 -11.5 -7.0 -.1 -7.0 -.8 .0 -.8 5.9 .0 5.9 11.4 .1 11.4 18.7 .2 18.9 26.5 .2 26.7 33.1 .3 33.4 41.6 .3 42.0 50.5 .4 51.0 SKYWALKER VIDEO Monthly closing cash for base scenario 60.0 50.0 40.0 30.0 20.0 10.0 .0 -10.0 -20.0 -30.0 Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Closing cash exceeds 50000 at the end of the year

DRA/K V Scenario analysis “Scenarios are discrete internally consistent views of how the world will look in the future, which can be selected to bound the possible range of outcomes that might occur.” Michael Porter in “Competitive Strategy” “Shell flavour” of scenarios Scenarios should present testing conditions for the business. The future will of course be different from all of these views/scenarios, but if the company is prepared to cope with any of them, it will be able to cope with the real world. Do not assign probabilities to scenarios!

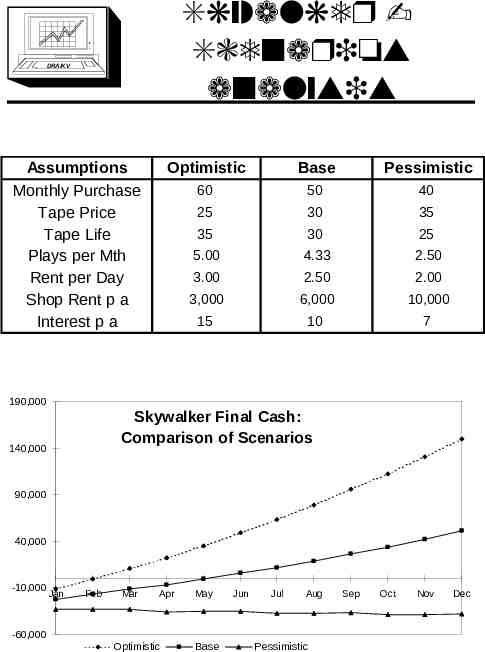
Skywalker Scenarios analysis DRA/K V Assumptions Monthly Purchase Tape Price Tape Life Plays per Mth Rent per Day Shop Rent p a Interest p a Optimistic Base Pessimistic 60 50 40 25 30 35 35 30 25 5.00 4.33 2.50 3.00 2.50 2.00 3,000 6,000 10,000 15 10 7 190,000 Skywalker Final Cash: Comparison of Scenarios 140,000 90,000 40,000 -10,000 Jan Feb Mar Apr May Jun Jul Aug -60,000 Optimistic Base Pessimistic Sep Oct Nov Dec

DRA/K V Sensitivity analysis Explore robustness of results to variations in model parameters Understand and challenge assumptions Methodology Identify variables to which results are particularly sensitive and those to which they are relatively insensitive Gain an indication into range over which results might vary, thus assessing the risks Tools – What-if questions – One-way sensitivity analysis – Two-way sensitivity analysis – Tornado diagrams – Spider plots

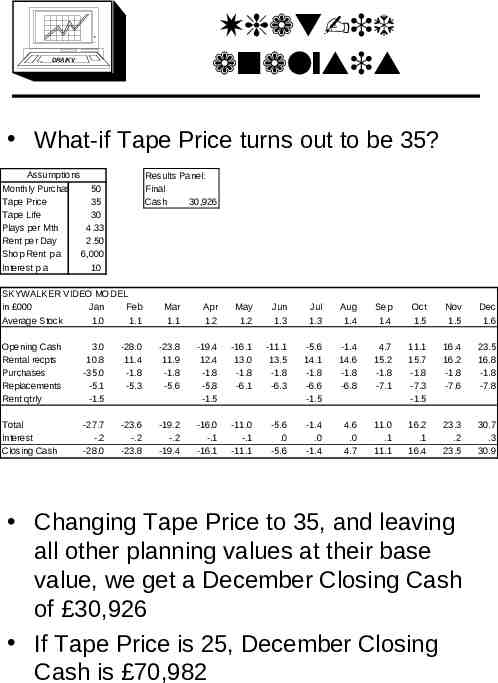
What-if analysis DRA/K V What-if Tape Price turns out to be 35? Assumptions Monthly Purchase 50 Tape Price 35 Tape Life 30 Plays per Mth 4.33 Rent per Day 2.50 Shop Rent p a 6,000 Interest p a 10 Results Panel: Final Cash 30,926 SKYWALKER VIDEO MODEL in 000 Jan Feb Average Stock 1.0 1.1 Mar 1.1 Apr 1.2 May 1.2 Jun 1.3 Jul 1.3 Aug 1.4 Sep 1.4 Oct 1.5 Nov 1.5 Dec 1.6 Opening Cash Rental recpts Purchases Replacements Rent qtrly 3.0 10.8 -35.0 -5.1 -1.5 -28.0 11.4 -1.8 -5.3 -23.8 11.9 -1.8 -5.6 -19.4 12.4 -1.8 -5.8 -1.5 -16.1 13.0 -1.8 -6.1 -11.1 13.5 -1.8 -6.3 -5.6 14.1 -1.8 -6.6 -1.5 -1.4 14.6 -1.8 -6.8 4.7 15.2 -1.8 -7.1 11.1 15.7 -1.8 -7.3 -1.5 16.4 16.2 -1.8 -7.6 23.5 16.8 -1.8 -7.8 Total Interest Closing Cash -27.7 -.2 -28.0 -23.6 -.2 -23.8 -19.2 -.2 -19.4 -16.0 -.1 -16.1 -11.0 -.1 -11.1 -5.6 .0 -5.6 -1.4 .0 -1.4 4.6 .0 4.7 11.0 .1 11.1 16.2 .1 16.4 23.3 .2 23.5 30.7 .3 30.9 Changing Tape Price to 35, and leaving all other planning values at their base value, we get a December Closing Cash of 30,926 If Tape Price is 25, December Closing Cash is 70,982

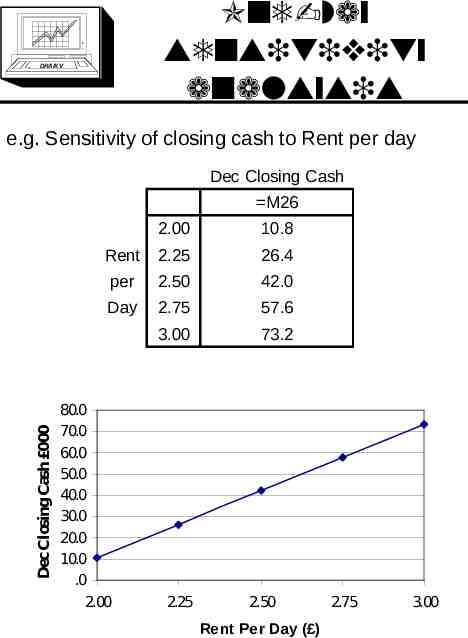
One-way sensitivity analsysis DRA/K V e.g. Sensitivity of closing cash to Rent per day Dec Closing Cash Dec Closing Cash 000 M26 2.00 10.8 Rent 2.25 26.4 per 2.50 42.0 Day 2.75 57.6 3.00 73.2 80.0 70.0 60.0 50.0 40.0 30.0 20.0 10.0 .0 2.00 2.25 2.50 Rent Per Day ( ) 2.75 3.00

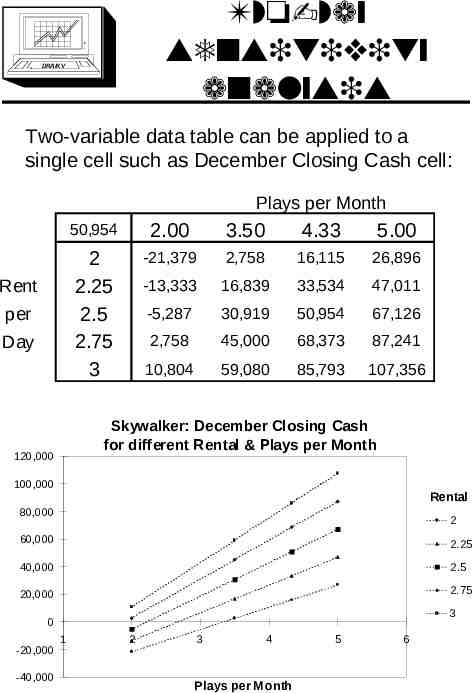
Two-way sensitivity analysis DRA/K V Two-variable data table can be applied to a single cell such as December Closing Cash cell: Plays per Month Rent per Day 50,954 2.00 3.50 4.33 5.00 2 2.25 2.5 2.75 3 -21,379 2,758 16,115 26,896 -13,333 16,839 33,534 47,011 -5,287 30,919 50,954 67,126 2,758 45,000 68,373 87,241 10,804 59,080 85,793 107,356 Skywalker: December Closing Cash for different Rental & Plays per Month 120,000 100,000 Rental 80,000 2 60,000 2.25 40,000 2.5 20,000 2.75 3 0 -20,000 -40,000 1 2 3 4 Plays per Month 5 6

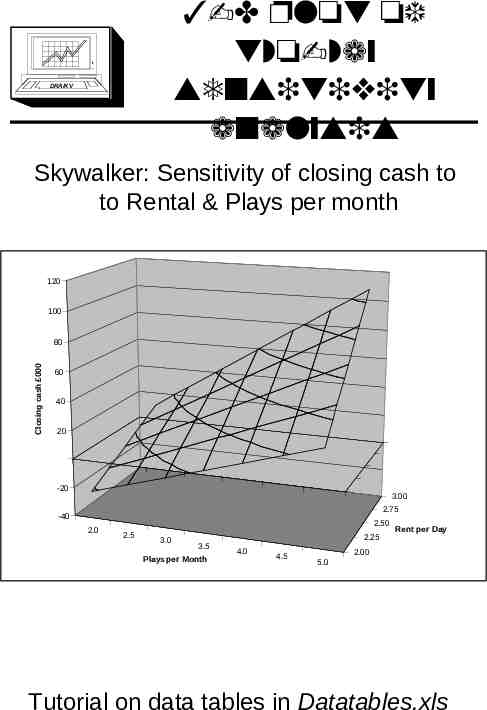
3-D plot of two-way sensitivity analysis DRA/K V Skywalker: Sensitivity of closing cash to to Rental & Plays per month 120 100 Closing cash 000 80 60 40 20 -20 3.00 2.75 -40 2.0 2.50 2.5 3.0 3.5 Plays per Month 2.25 4.0 4.5 Rent per Day 2.00 5.0 Tutorial on data tables in Datatables.xls

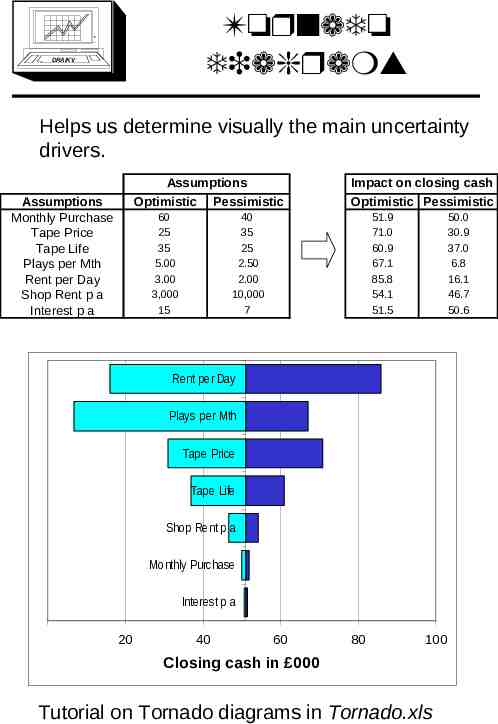
Tornado diagrams DRA/K V Helps us determine visually the main uncertainty drivers. Assumptions Optimistic Pessimistic Assumptions Monthly Purchase Tape Price Tape Life Plays per Mth Rent per Day Shop Rent p a Interest p a 60 25 35 5.00 3.00 3,000 15 Impact on closing cash Optimistic Pessimistic 40 35 25 2.50 2.00 10,000 7 51.9 71.0 60.9 67.1 85.8 54.1 51.5 50.0 30.9 37.0 6.8 16.1 46.7 50.6 Rent per Day Plays per Mth Tape Price Tape Life Shop Rent p a Monthly Purchase Interest p a 20 40 60 80 100 Closing cash in 000 Tutorial on Tornado diagrams in Tornado.xls

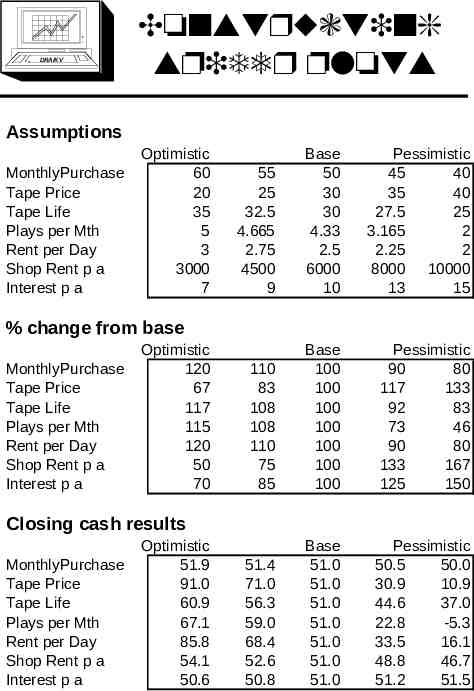
DRA/K V Constructing spider plots Assumptions MonthlyPurchase Tape Price Tape Life Plays per Mth Rent per Day Shop Rent p a Interest p a Optimistic 60 20 35 5 3 3000 7 55 25 32.5 4.665 2.75 4500 9 Base 50 30 30 4.33 2.5 6000 10 Pessimistic 45 40 35 40 27.5 25 3.165 2 2.25 2 8000 10000 13 15 110 83 108 108 110 75 85 Base 100 100 100 100 100 100 100 Pessimistic 90 80 117 133 92 83 73 46 90 80 133 167 125 150 51.4 71.0 56.3 59.0 68.4 52.6 50.8 Base 51.0 51.0 51.0 51.0 51.0 51.0 51.0 Pessimistic 50.5 50.0 30.9 10.9 44.6 37.0 22.8 -5.3 33.5 16.1 48.8 46.7 51.2 51.5 % change from base MonthlyPurchase Tape Price Tape Life Plays per Mth Rent per Day Shop Rent p a Interest p a Optimistic 120 67 117 115 120 50 70 Closing cash results MonthlyPurchase Tape Price Tape Life Plays per Mth Rent per Day Shop Rent p a Interest p a Optimistic 51.9 91.0 60.9 67.1 85.8 54.1 50.6

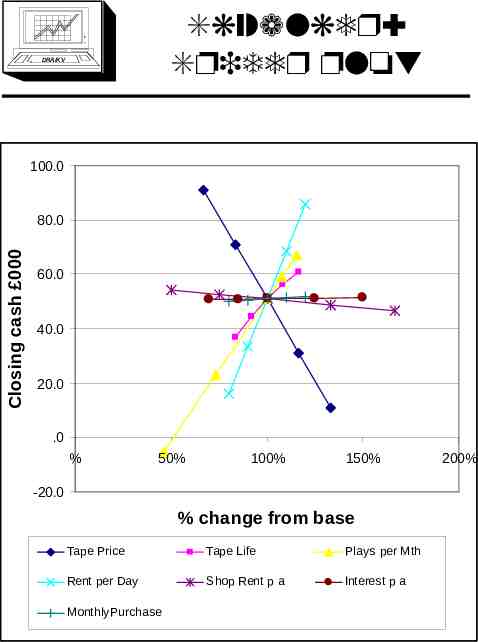
Skywalker: Spider plot DRA/K V 100.0 Closing cash 000 80.0 60.0 40.0 20.0 .0 % 50% 100% 150% -20.0 % change from base Tape Price Tape Life Plays per Mth Rent per Day Shop Rent p a Interest p a MonthlyPurchase 200%

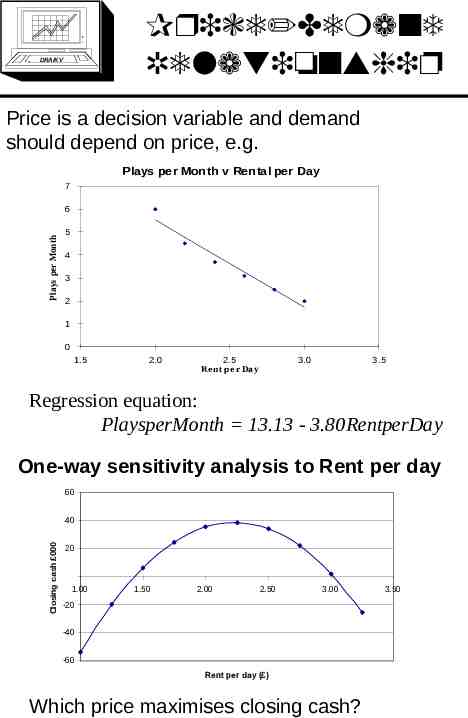
Price/Demand Relationship DRA/K V Price is a decision variable and demand should depend on price, e.g. Plays per Month v Rental per Day 7 Plays per Month 6 5 4 3 2 1 0 1.5 2.0 2.5 R ent pe r Da y 3.0 3.5 Regression equation: PlaysperMonth 13.13 - 3.80RentperDay One-way sensitivity analysis to Rent per day 60 Closing cash 000 40 20 1.00 1.50 2.00 2.50 3.00 -20 -40 -60 Rent per day ( ) Which price maximises closing cash? 3.50

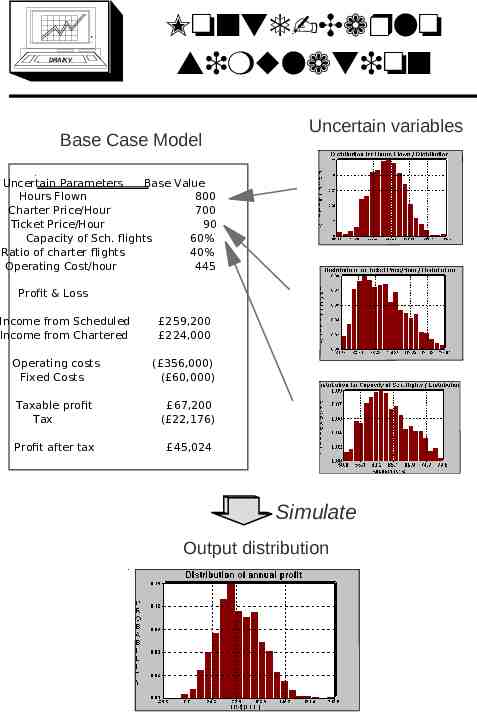
DRA/K V Monte-Carlo simulation Base Case Model Uncertain variables Uncertain Parameters Base Value Hours Flown 800 Charter Price/Hour 700 Ticket Price/Hour 90 Capacity of Sch. flights 60% Ratio of charter flights 40% Operating Cost/hour 445 Profit & Loss Income from Scheduled Income from Chartered Operating costs Fixed Costs 259,200 224,000 ( 356,000) ( 60,000) Taxable profit Tax 67,200 ( 22,176) Profit after tax 45,024 Simulate Output distribution

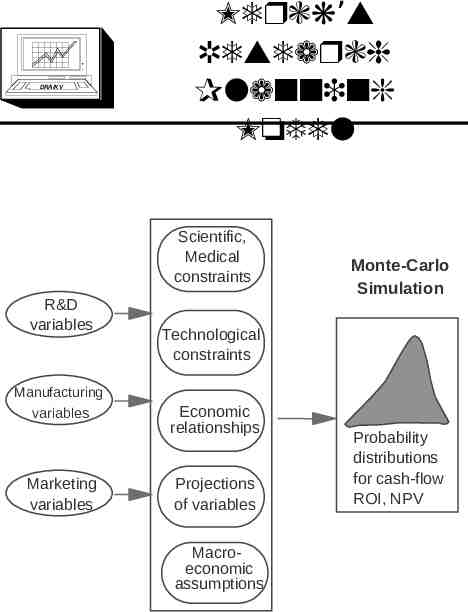
DRA/K V Merck’s Research Planning Model Scientific, Medical constraints R&D variables Manufacturing variables Marketing variables Monte-Carlo Simulation Technological constraints Economic relationships Projections of variables Macroeconomic assumptions Probability distributions for cash-flow ROI, NPV

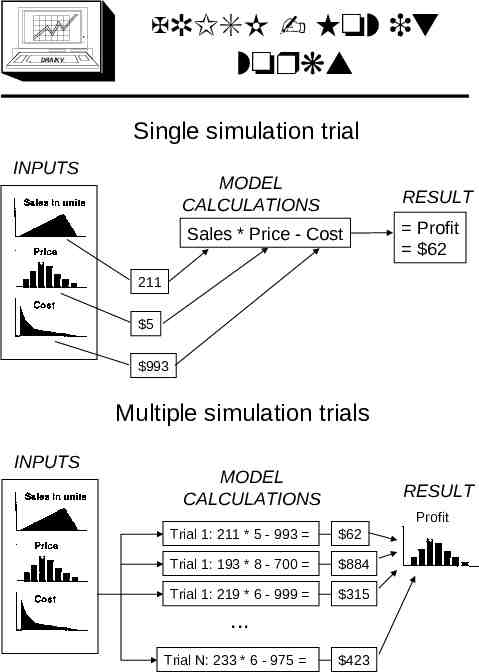
DRA/K V @RISK - How it works Single simulation trial INPUTS MODEL CALCULATIONS RESULT Sales * Price - Cost Profit 62 211 5 993 Multiple simulation trials INPUTS MODEL CALCULATIONS RESULT Profit Trial 1: 211 * 5 - 993 62 Trial 1: 193 * 8 - 700 884 Trial 1: 219 * 6 - 999 315 . Trial N: 233 * 6 - 975 423

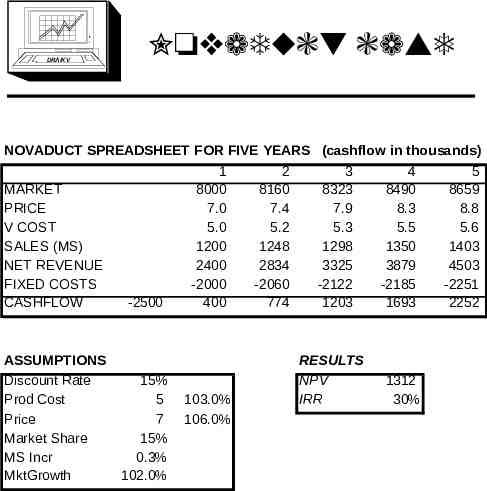
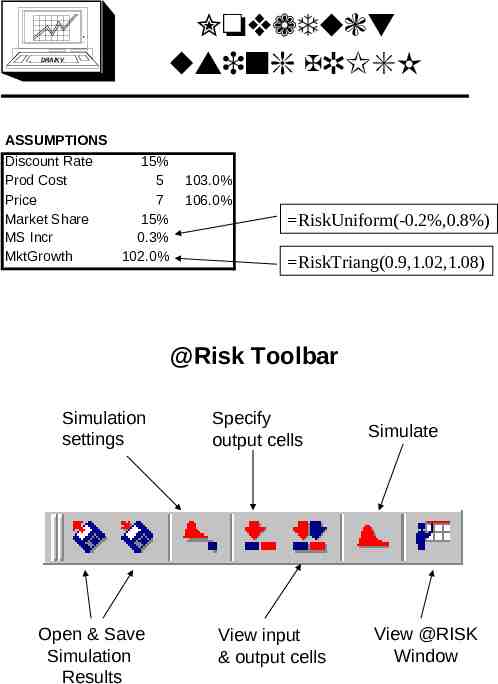
DRA/K V Novaduct case NOVADUCT SPREADSHEET FOR FIVE YEARS 1 2 MARKET 8000 8160 PRICE 7.0 7.4 V COST 5.0 5.2 SALES (MS) 1200 1248 NET REVENUE 2400 2834 FIXED COSTS -2000 -2060 CASHFLOW -2500 400 774 ASSUMPTIONS Discount Rate Prod Cost Price Market Share MS Incr MktGrowth 15% 5 7 15% 0.3% 102.0% 103.0% 106.0% (cashflow in thousands) 3 4 5 8323 8490 8659 7.9 8.3 8.8 5.3 5.5 5.6 1298 1350 1403 3325 3879 4503 -2122 -2185 -2251 1203 1693 2252 RESULTS NPV IRR 1312 30%

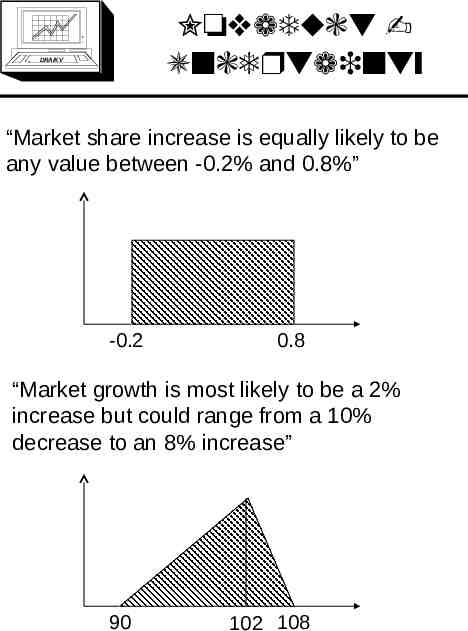
Novaduct Uncertainty DRA/K V “Market share increase is equally likely to be any value between -0.2% and 0.8%” -0.2 0.8 “Market growth is most likely to be a 2% increase but could range from a 10% decrease to an 8% increase” 90 102 108

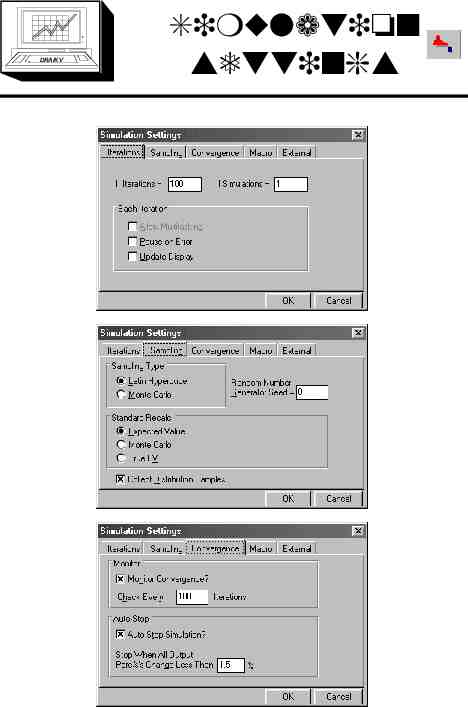
DRA/K V Using @RISK 1. Introduce uncertainty into base model eg RiskUniform(min, max) RiskTriang(min, most likely, max) RiskNormal(mean, std.dev.) 2. Select output cells (Cells for which we want simulation results) 3. Select simulation settings Number of iterations, random number seed 4. Execute simulation 5. View results Graphs, summary statistics 6. Return to spreadsheet and possibly repeat previous steps

Novaduct using @RISK DRA/K V ASSUMPTIONS Discount Rate Prod Cost Price Market Share MS Incr MktGrowth 15% 5 7 15% 0.3% 102.0% 103.0% 106.0% RiskUniform(-0.2%,0.8%) RiskTriang(0.9,1.02,1.08) @Risk Toolbar Simulation settings Open & Save Simulation Results Specify output cells View input & output cells Simulate View @RISK Window

DRA/K V Simulation settings

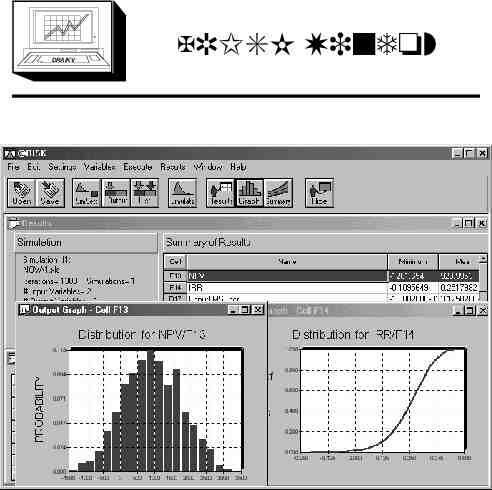
DRA/K V @RISK Window

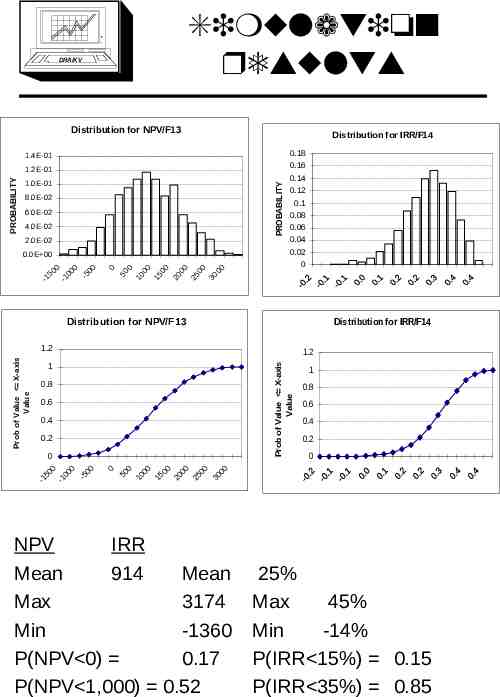
Simulation results DRA/K V Distribution for NPV/F13 Distribution for IRR/F14 0.18 0.16 1.4E-01 1.0E-01 PROBABILITY PROBABILITY 1.2E-01 8.0E-02 6.0E-02 4.0E-02 2.0E-02 00 00 0.1 0.08 0.06 0.04 0.02 0 30 00 00 25 20 0 00 15 10 0 50 0 00 -5 0 -1 0 -1 5 00 0.0E 00 0.14 0.12 Distribution for IRR/F14 Distribution for NPV/F13 1.2 1 Prob of Value X-axis Value Prob of Value X-axis Value 1.2 0.8 0.6 0.4 0.2 0.8 0.6 0.4 0.2 0 50 0 10 00 15 00 20 00 25 00 30 00 0 -1 50 0 -1 00 0 -5 00 0 1 NPV IRR Mean 914 Mean Max 3174 Min -1360 P(NPV 0) 0.17 P(NPV 1,000) 0.52 25% Max 45% Min -14% P(IRR 15%) 0.15 P(IRR 35%) 0.85

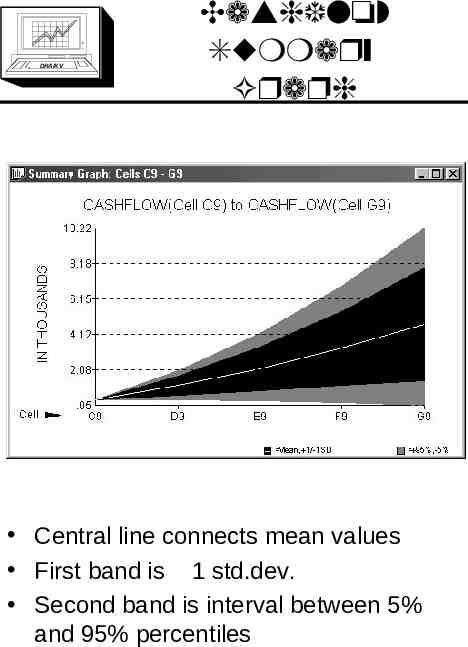
DRA/K V Cashflow Summary Graph Central line connects mean values First band is 1 std.dev. Second band is interval between 5% and 95% percentiles

DRA/K V Summary Single point forecasts are dangerous! Challenge assumptions Scenario Planning Sensitivity analysis – Data tables – Tornado diagrams Monte-Carlo simulation Preparation for Workshop – Datatables.xls and Tornado.xls – @RISK tutorial – Exercises