doc.: IEEE 802.11-03/0865r0 LDPC FEC for IEEE 802.11n

doc.: IEEE 802.11-03/0865r0 LDPC FEC for IEEE 802.11n Applications Eric Jacobsen Intel Labs Communications Technology Laboratory November 10, 2003 Submission

November 2003 doc.: IEEE 802.11-03/0865r0 Agenda Background – why LDPCs? Fitting LDPCs to WLAN Details of candidate code Performance and use of candidate code Complexity analysis Summary Submission Slide 2

November 2003 doc.: IEEE 802.11-03/0865r0 Candidate Iterative FECs Turbo Codes (PCCC or SCCC) – High complexity – Poor performance with short blocks – IP Issues Turbo Product Codes – – – – Medium Complexity Best performance at R 0.8 Poor performance with short blocks Possible IP issues Low Density Parity Check Codes (LDPCs) – Invented in 1962 – No basic IP! – Potential for low complexity – constituent codes are Parity Check relationships – Extremely good performance with long blocks (C-0.0045dB!) – Very good performance with short blocks (Lin) – Eliminate channel interleaver Submission Slide 3

November 2003 doc.: IEEE 802.11-03/0865r0 LDPC Codes solve several problems Close the large gap between current and theoretical performance – Only known solution for good performance with small block sizes Enable Adaptive Bit Loading by eliminating the channel bit interleaver – LDPCs incorporate the required randomization into the code – These are the only known codes that do this! – This also provides a significant complexity reduction Offsets complexity of code – Decoupling the FEC and modulation increases flexibility Submission Slide 4

November 2003 doc.: IEEE 802.11-03/0865r0 Low Density Parity Check FEC Iterative decoding of simple parity check codes Published examples of good performance with short blocks – Kou, Lin, Fossorier, Trans IT, Nov. 2001 Near-capacity performance with long blocks – Very near! - Chung, et al, “On the design of low-density parity-check codes within 0.0045dB of the Shannon limit”, IEEE Comm. Lett., Feb. 2001 Complexity fears, especially in encoder Implementation Challenges – Many options wrt decoding algorithms, architectures, techniques Submission Slide 5

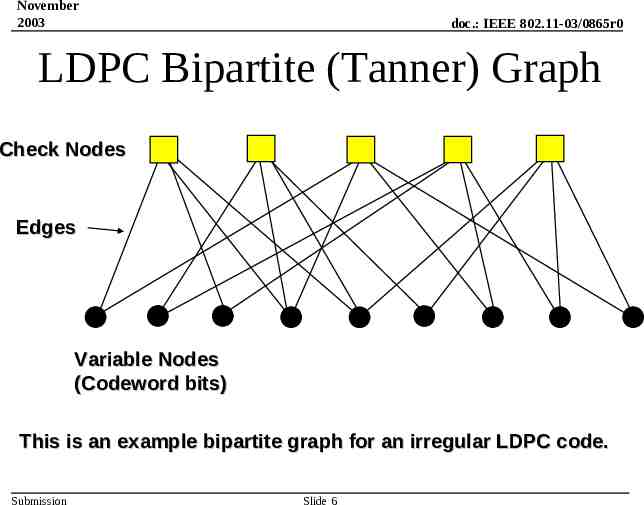
November 2003 doc.: IEEE 802.11-03/0865r0 LDPC Bipartite (Tanner) Graph Check Nodes Edges Variable Nodes (Codeword bits) This is an example bipartite graph for an irregular LDPC code. Submission Slide 6

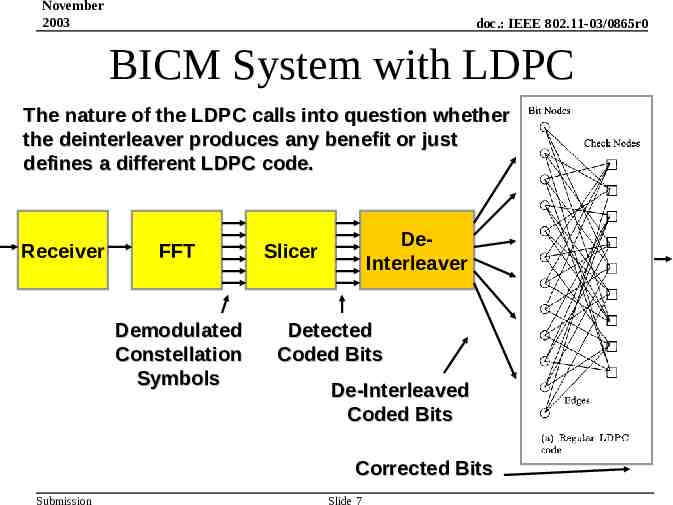
November 2003 doc.: IEEE 802.11-03/0865r0 BICM System with LDPC The nature of the LDPC calls into question whether the deinterleaver produces any benefit or just defines a different LDPC code. Receiver FFT Demodulated Constellation Symbols DeInterleaver Slicer Detected Coded Bits De-Interleaved Coded Bits Corrected Bits Submission Slide 7

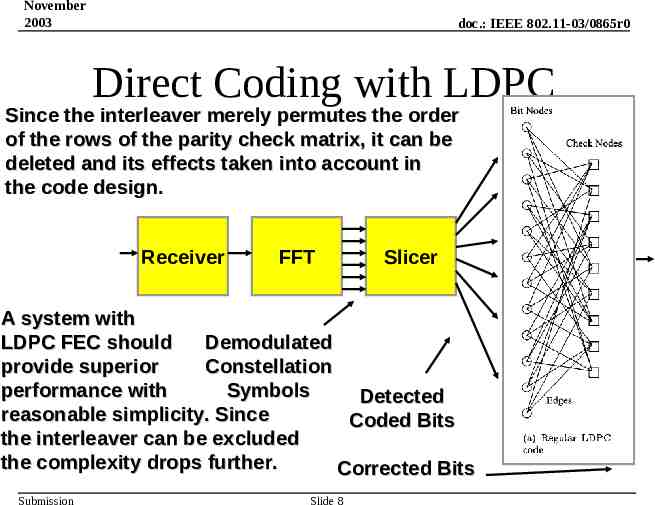
November 2003 doc.: IEEE 802.11-03/0865r0 Direct Coding with LDPC Since the interleaver merely permutes the order of the rows of the parity check matrix, it can be deleted and its effects taken into account in the code design. Receiver FFT Slicer A system with LDPC FEC should Demodulated provide superior Constellation performance with Symbols Detected reasonable simplicity. Since Coded Bits the interleaver can be excluded the complexity drops further. Corrected Bits Submission Slide 8

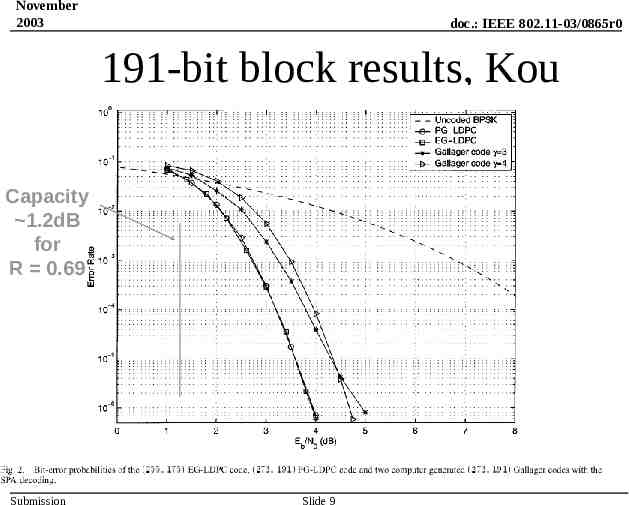
November 2003 doc.: IEEE 802.11-03/0865r0 191-bit block results, Kou Capacity 1.2dB for R 0.69 Submission Slide 9

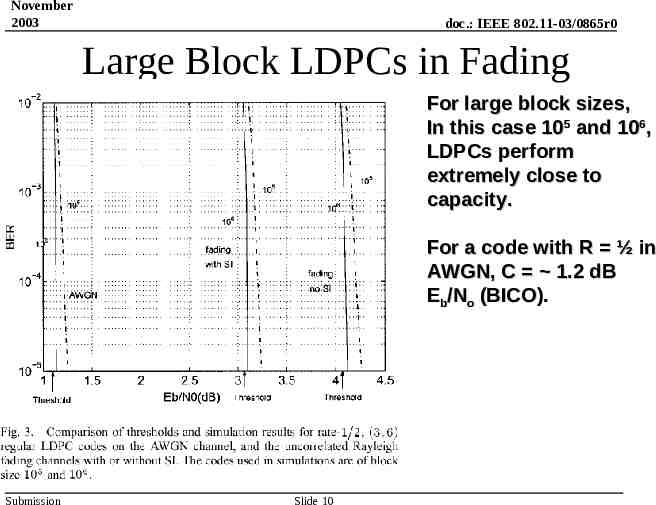
November 2003 doc.: IEEE 802.11-03/0865r0 Large Block LDPCs in Fading For large block sizes, In this case 105 and 106, LDPCs perform extremely close to capacity. For a code with R ½ in AWGN, C 1.2 dB Eb/No (BICO). Submission Slide 10

November 2003 doc.: IEEE 802.11-03/0865r0 Candidate LDPC Code (2000, 1600) code, R 0.8 – Long enough for good performance, short enough to implement – BER in AWGN is 1.5dB from Capacity at Pe 10-5 Column weights are controlled by the code design Four edges per information bit, two per parity bit – Last parity bit has one edge 18 edges per check node (regular in H1) Total of 7199 edges Simplified Encoder BCJR or Min-Sum decoding algorithm – Min-Sum costs 0.3dB in peformance, cuts gate count Submission Slide 11

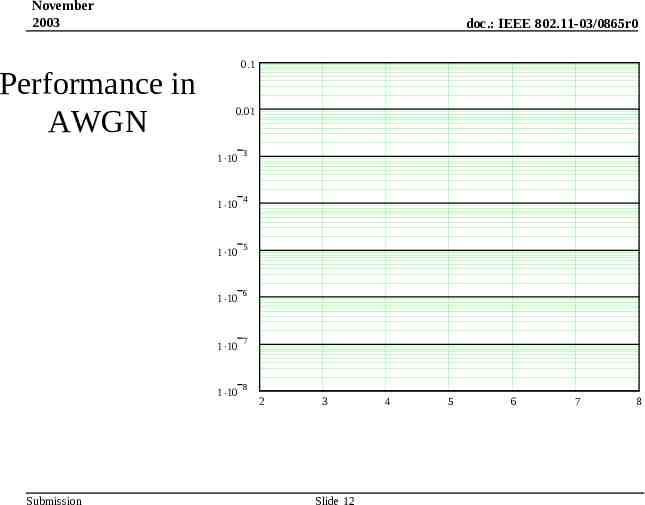
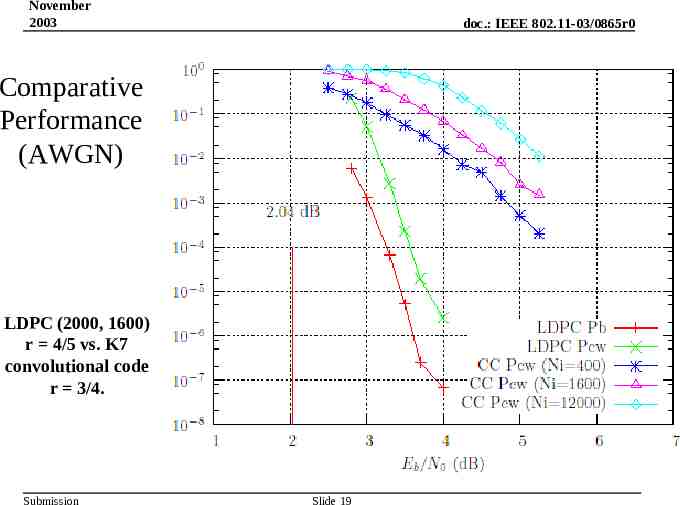
November 2003 doc.: IEEE 802.11-03/0865r0 0.1 Performance in AWGN At Pe 10-5 the LDPC code is 1.5dB from Capacity. 0.01 1 10 3 1 10 4 1 10 5 1 10 6 1 10 7 1 10 8 BER Capacity for R 0.8 is 2.044dB, shown with a vertical dashed red line. 2.044 2 3 Uncoded R 3/4, Viterbi R 7/8, Viterbi R 0.8, LDPC Submission Slide 12 4 5 Eb/No 6 7 8

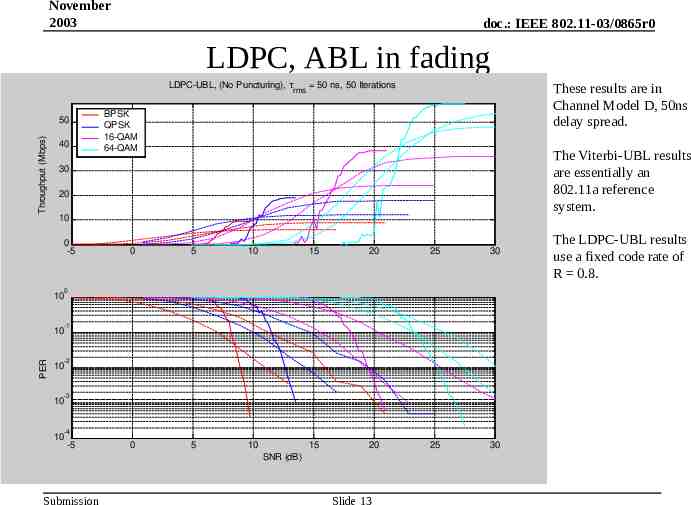
November 2003 doc.: IEEE 802.11-03/0865r0 LDPC, ABL in fading LDPC-UBL, (No Puncturing), rms Throughput (Mbps) 50 40 These results are in Channel Model D, 50ns delay spread. 50 ns, 50 Iterations BPSK QPSK 16-QAM 64-QAM The Viterbi-UBL results are essentially an 802.11a reference system. 30 20 10 0 -5 0 5 10 0 5 10 15 20 25 30 15 20 25 30 0 10 -1 PER 10 -2 10 -3 10 -4 10 -5 SNR (dB) Submission Slide 13 The LDPC-UBL results use a fixed code rate of R 0.8.

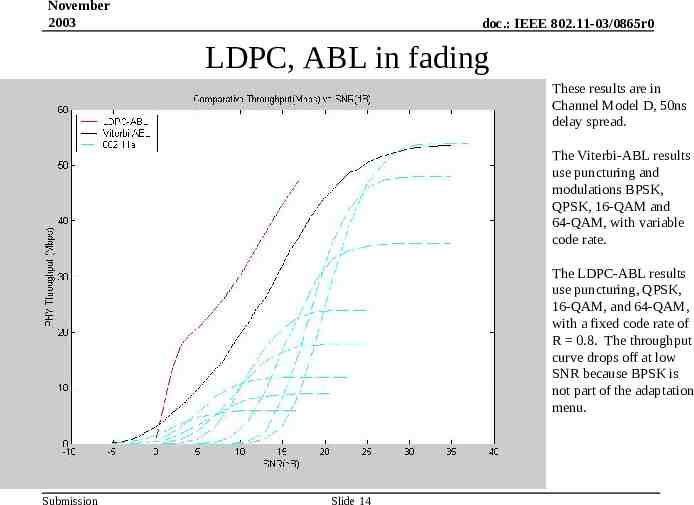
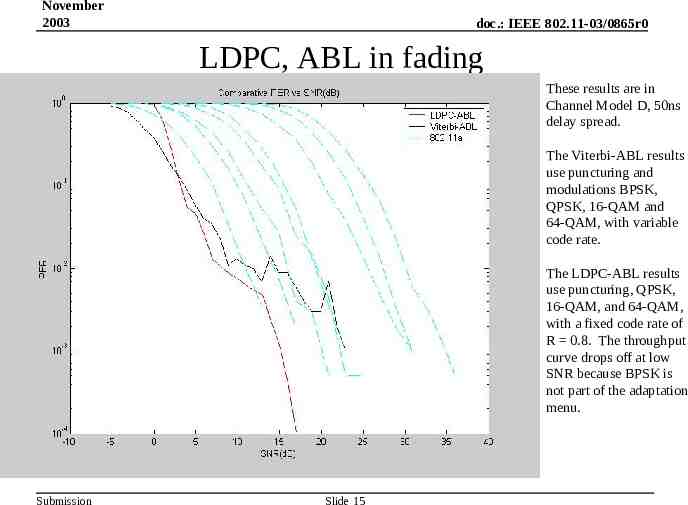
November 2003 doc.: IEEE 802.11-03/0865r0 LDPC, ABL in fading These results are in Channel Model D, 50ns delay spread. The Viterbi-ABL results use puncturing and modulations BPSK, QPSK, 16-QAM and 64-QAM, with variable code rate. The LDPC-ABL results use puncturing, QPSK, 16-QAM, and 64-QAM, with a fixed code rate of R 0.8. The throughput curve drops off at low SNR because BPSK is not part of the adaptation menu. Submission Slide 14

November 2003 doc.: IEEE 802.11-03/0865r0 LDPC, ABL in fading These results are in Channel Model D, 50ns delay spread. The Viterbi-ABL results use puncturing and modulations BPSK, QPSK, 16-QAM and 64-QAM, with variable code rate. The LDPC-ABL results use puncturing, QPSK, 16-QAM, and 64-QAM, with a fixed code rate of R 0.8. The throughput curve drops off at low SNR because BPSK is not part of the adaptation menu. Submission Slide 15

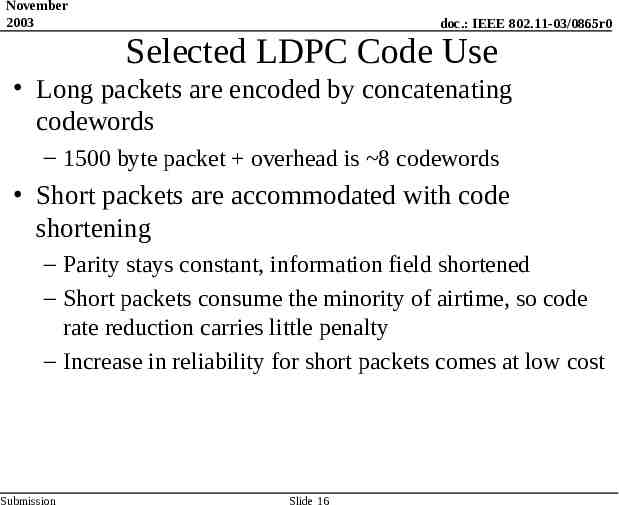
November 2003 doc.: IEEE 802.11-03/0865r0 Selected LDPC Code Use Long packets are encoded by concatenating codewords – 1500 byte packet overhead is 8 codewords Short packets are accommodated with code shortening – Parity stays constant, information field shortened – Short packets consume the minority of airtime, so code rate reduction carries little penalty – Increase in reliability for short packets comes at low cost Submission Slide 16

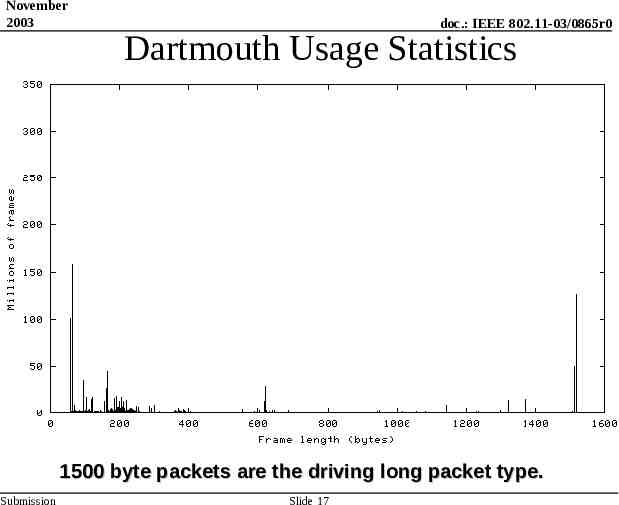
November 2003 doc.: IEEE 802.11-03/0865r0 Dartmouth Usage Statistics 1500 byte packets are the driving long packet type. Submission Slide 17

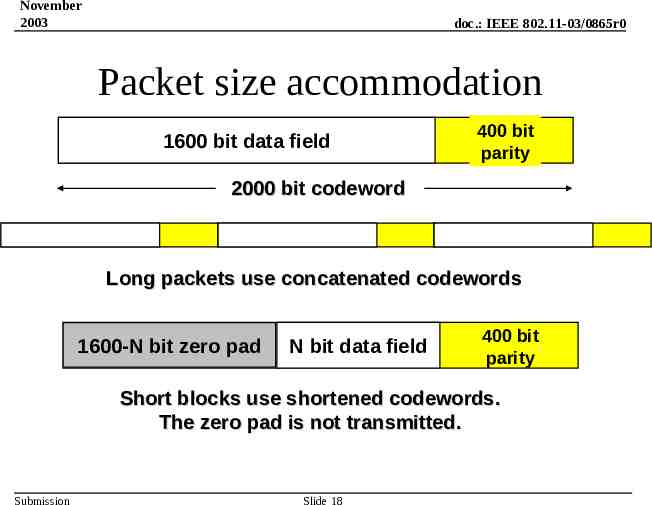
November 2003 doc.: IEEE 802.11-03/0865r0 Packet size accommodation 1600 bit data field 400 bit parity 2000 bit codeword Long packets use concatenated codewords 1600-N bit zero pad N bit data field 400 bit parity Short blocks use shortened codewords. The zero pad is not transmitted. Submission Slide 18

November 2003 doc.: IEEE 802.11-03/0865r0 Comparative Performance (AWGN) LDPC (2000, 1600) r 4/5 vs. K7 convolutional code r 3/4. Submission Slide 19

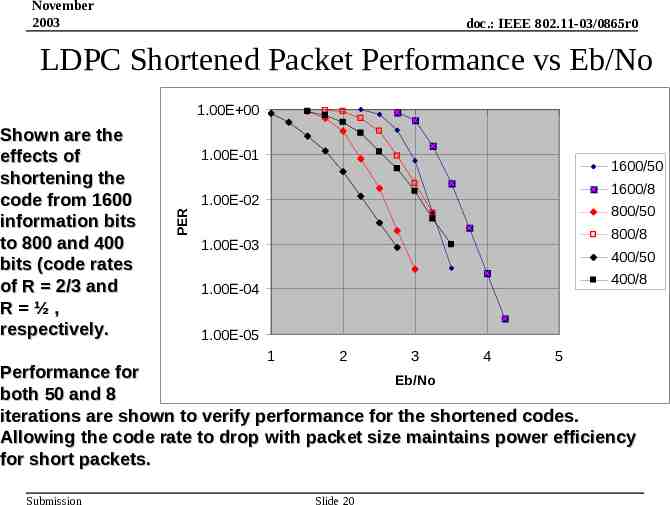
November 2003 doc.: IEEE 802.11-03/0865r0 LDPC Shortened Packet Performance vs Eb/No 1.00E 00 1.00E-01 1600/50 1600/8 1.00E-02 800/50 PER Shown are the effects of shortening the code from 1600 information bits to 800 and 400 bits (code rates of R 2/3 and R ½, respectively. 800/8 1.00E-03 400/50 400/8 1.00E-04 1.00E-05 1 2 3 4 5 Performance for Eb/No both 50 and 8 iterations are shown to verify performance for the shortened codes. Allowing the code rate to drop with packet size maintains power efficiency for short packets. Submission Slide 20

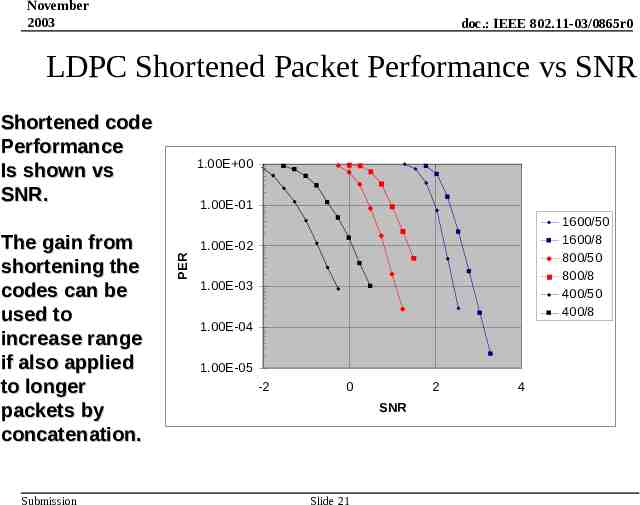
November 2003 doc.: IEEE 802.11-03/0865r0 LDPC Shortened Packet Performance vs SNR Shortened code Performance Is shown vs SNR. Submission 1.00E-01 1600/50 1600/8 800/50 800/8 400/50 400/8 1.00E-02 PER The gain from shortening the codes can be used to increase range if also applied to longer packets by concatenation. 1.00E 00 1.00E-03 1.00E-04 1.00E-05 -2 0 2 SNR Slide 21 4

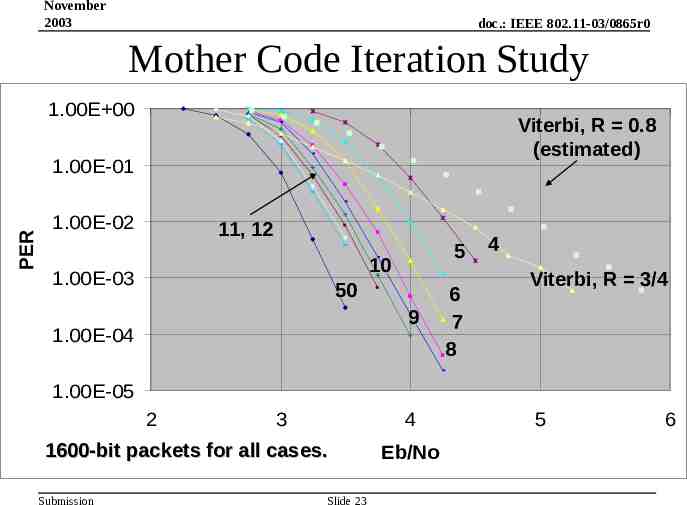
November 2003 doc.: IEEE 802.11-03/0865r0 Iteration Management LDPCs are iteratively decoded – The number of iterations affects the code performance – The number of iterations also affects the complexity Submission Slide 22

November 2003 doc.: IEEE 802.11-03/0865r0 Mother Code Iteration Study 1.00E 00 Viterbi, R 0.8 (estimated) PER 1.00E-01 1.00E-02 11, 12 5 10 1.00E-03 50 9 1.00E-04 6 7 8 4 Viterbi, R 3/4 1.00E-05 2 3 4 1600-bit packets for all cases. Submission Slide 23 Eb/No 5 6

November 2003 doc.: IEEE 802.11-03/0865r0 Complexity Tradeoffs Gate and memory complexity decrease with increasing clock rate – Serialization of processing allows gate and memory reuse Gate complexity increases with number of iterations – Memory stays constant BCJR more than 2x gate complexity over Min-Sum kernel – 0.3dB performance improvement – If memory complexity drives, then BCJR is a good option Submission Slide 24

November 2003 doc.: IEEE 802.11-03/0865r0 Latency Drives For any block code for 802.11 the MAC latency requirements will drive 1600 bits at 240 Mbps takes 6.6us to receive SIFS budget drives, so for worst-case we assume a 1us budget allocated to the FEC block Submission Slide 25

November 2003 doc.: IEEE 802.11-03/0865r0 Analysis Assumptions 240 Mbps target – Should encompass most modes Eight iterations Two processing clocks per information bit – Keep duty cycle low, reduces power consumption? BCJR algorithm Submission Slide 26

November 2003 Gates – – – – – doc.: IEEE 802.11-03/0865r0 Complexity Estimates 1us 240 cycles at 240 MHz Computation gates, BCJR 124k gates Additional control, sums, etc., 40k gates Estimated BCJR total gate count 164k gates Estimated Min-Sum total gate count 98k gates Memory – Scratchpad, computation, buffering 120k bits – Code address ROM 93.6k bits Submission Slide 27

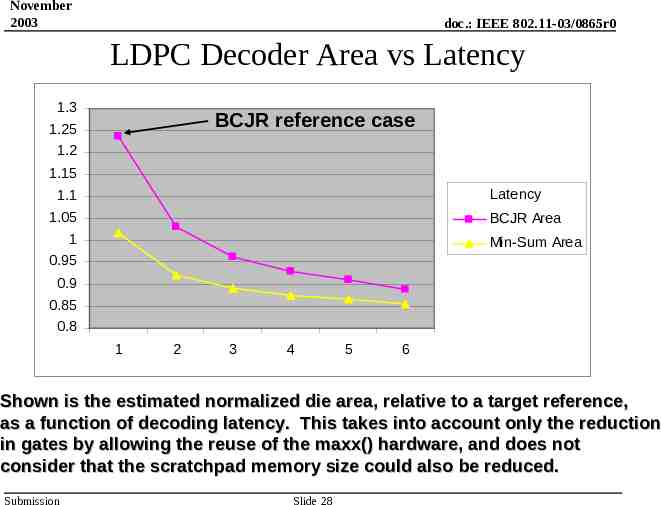
November 2003 doc.: IEEE 802.11-03/0865r0 LDPC Decoder Area vs Latency 1.3 BCJR reference case 1.25 1.2 1.15 1.1 1.05 1 0.95 Latency BCJR Area Min-Sum Area 0.9 0.85 0.8 1 2 3 4 5 6 Shown is the estimated normalized die area, relative to a target reference, as a function of decoding latency. This takes into account only the reduction in gates by allowing the reuse of the maxx() hardware, and does not consider that the scratchpad memory size could also be reduced. Submission Slide 28

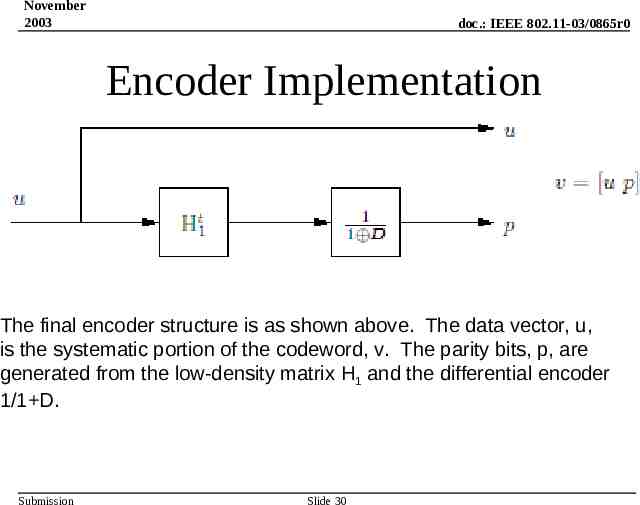
November 2003 doc.: IEEE 802.11-03/0865r0 Encoder Complexity v u G The generic block encoder definition. A typical LDPC generator matrix, G, is high density for a low density parity check matrix H. t t v u G [u uP ] [u uH 1 H 2 ] By carefully partitioning G, the low density H matrix may be used and separated into two portions, H1 and H2, where H2 takes the lowdensity form shown. The inverse transpose of H2 can then be implemented as a differential encoder. t v [u uH 1 H 2 Submission t 1 t ] u uH 1 1 D Slide 29

November 2003 doc.: IEEE 802.11-03/0865r0 Encoder Implementation The final encoder structure is as shown above. The data vector, u, is the systematic portion of the codeword, v. The parity bits, p, are generated from the low-density matrix H1 and the differential encoder 1/1 D. Submission Slide 30

November 2003 doc.: IEEE 802.11-03/0865r0 Complexity Summary 164k gates computation and control with BCJR 98k gates computation and control with Min-Sum – This is to achieve 1us decode time. Gate counts drop dramatically as latency is allowed to increase. Memory estimate is 120k bits of RAM and 93.6k bits of control ROM This is a conservative budgetary estimate. Other decoding algorithms or trick implementations may yield different results. Submission Slide 31

November 2003 Summary doc.: IEEE 802.11-03/0865r0 This LDPC code by itself provides 2-3 dB of gain – Implementation is practical – much flexibility in approach – Less than 1.5dB from AWGN Capacity at Pe 10-5 with a 1600-bit data block and R 0.8 Flexible in code rate and data block size – Shortening schemes allow no restrictions on data block size – Observing OFDM symbol boundaries is not required – Eliminates Channel Interleaver Decouples FEC from modulation, MIMO/SISO, higher-order modulation, etc. Submission Slide 32

doc.: IEEE 802.11-03/0865r0 Backup Submission

November 2003 doc.: IEEE 802.11-03/0865r0 Partial Reference List TCM – G. Ungerboeck, “Channel Coding with Multilevel/Phase Signals”, IEEE Trans. IT, Vol. IT-28, No. 1, January, 1982 BICM – G. Caire, G. Taricco, and E. Biglieri, “Bit-Interleaved Coded Modulation”, IEEE Trans. On IT, May, 1998 LDPC – Ryan, W., “An Introduction to Low Density Parity Check Codes”, UCLA Short Course Notes, April, 2001 – Kou, Lin, Fossorier, “Low Density Parity Check Codes Based on Finite Geometries: A Rediscovery and New Results”, IEEE Transactions on Information Theory, Vol. 47, No. 7, November 2001 – R. Gallager, “Low-density parity-check codes”, IRE Trans. IT, Jan. 1962 – Chung, et al, “On the design of low-density parity-check codes within 0.0045dB of the Shannon limit”, IEEE Comm. Lett., Feb. 2001 – J. Hou, P. Siegel, and L. Milstein, “Performance Analysis and Code Optimisation for Low Density Parity-Check Codes on Rayleigh Fading Channels” IEEE JSAC, Vol. 19, No. 5, May, 2001 – L. Van der Perre, S. Thoen, P. Vandenameele, B. Gyselinckx, and M. Engels, “Adaptive loading strategy for a high speed OFDM-based WLAN”, Globecomm 98 – Numerous articles on recent developments LDPCs, IEEE Trans. On IT, Feb. 2001 Submission Slide 34

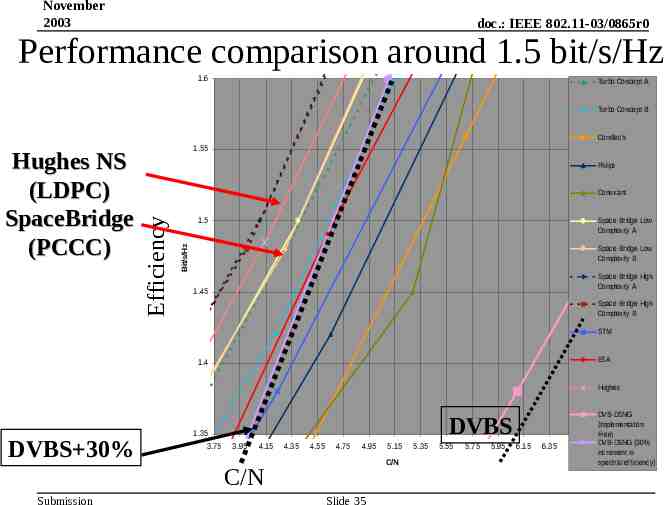
November 2003 doc.: IEEE 802.11-03/0865r0 Performance comparison around 1.5 bit/s/Hz 1.6 Turbo Concept A Turbo Concept B ComTech Philips Conexant 1.5 Space Bridge Low Complexity A Space Bridge Low Complexity B Bit/s/Hz Efficiency Hughes NS (LDPC) SpaceBridge (PCCC) 1.55 Space Bridge High Complexity A 1.45 Space Bridge High Complexity B STM ESA 1.4 Hughes DVBS 30% DVBS 1.35 3.75 3.95 4.15 4.35 4.55 4.75 4.95 C/N C/N Submission 5.15 Slide 35 5.35 5.55 5.75 5.95 6.15 6.35 DVB-DSNG (Implementation Free) DVB-DSNG (30% increment in spectral efficiency)