Distributed Consensus Reaching agreement is a fundamental problem

Distributed Consensus Reaching agreement is a fundamental problem in distributed computing. Some examples are Leader election / Mutual Exclusion Commit or Abort in distributed transactions Reaching agreement about which process has failed Clock phase synchronization Air traffic control system: all aircrafts must have the same view

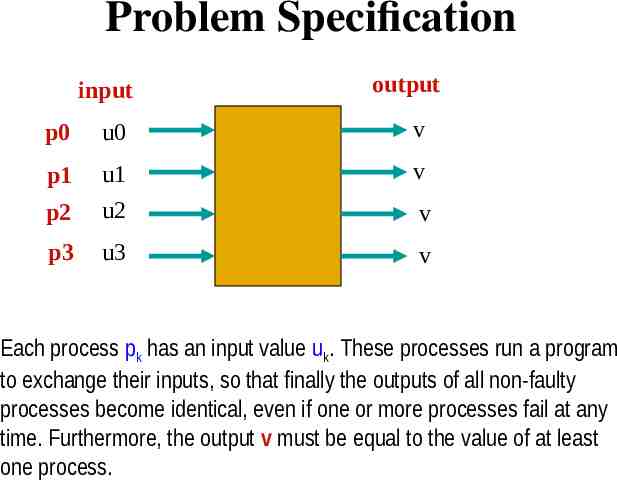
Problem Specification input output p0 u0 v p1 v p2 u1 u2 p3 u3 v v Each process pk has an input value uk. These processes run a program to exchange their inputs, so that finally the outputs of all non-faulty processes become identical, even if one or more processes fail at any time. Furthermore, the output v must be equal to the value of at least one process.

Problem Specification Termination. Every non-faulty process must eventually decide. Agreement. The final decision of every non-faulty process must be identical. Validity. If every non-faulty process begins with the same initial value v, then their final decision must be v.

Observation If there is no failure, then reaching consensus is trivial. All-to-all broadcast followed by a applying a choice function Consensus in presence of failures can however be complex. The complexity depends on the system model and the type of failures

Asynchronous Consensus Seven members of a busy household decided to hire a cook, since they do not have time to prepare their own food. Each member separately interviewed every applicant for the cook’s position. Depending on how it went, each member voted "yes" (means “hire”) or "no" (means “don't hire”). These members will now have to communicate with one another to reach a uniform final decision about whether the applicant will be hired. The process will be repeated with the next applicant, until someone is hired. Consider various modes of communication like shared memory or message passing. Also assume that one process (i.e. a member) may crash at any time.

Asynchronous Consensus Theorem. In a purely asynchronous distributed system, the consensus problem is impossible to solve if even a single process crashes. Result due to Fischer, Lynch, Patterson (commonly known as FLP 85). Received the most influential paper award of ACM PODC in 2001

Proof Bivalent and Univalent states A decision state is bivalent, if starting from that state, there exist two distinct executions leading to two distinct decision values 0 or 1. Otherwise it is univalent. A univalent state may be either 0-valent or 1-valent.

Proof (continued) Lemma. No execution can lead from a 0-valent to a 1-valent state or vice versa. Proof. Follows from the definition of 0-valent and 1-valent states.

Proof Lemma. Every consensus protocol must have a bivalent initial state. Proof by contradiction. Suppose not. Then consider the following input patterns: n-1 s[0] s[n] 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 {0-valent) {1-valent} What if process j crashes at the first step? there must be a j: s[j] is 0-valent s[j 1] is 1-valent

Proof of FLP (continued) Lemma. bivalent In a consensus protocol, starting from Q any initial bivalent state S, there must exist a reachable bivalent state T, such that every action taken by some process p in state T leads to bivalent bivalent S bivalent R action 0 bivalent U action 1 T action 0 action 1 either a 0 valent or a 1-valent state. R0 Note that bivalent states should not form a cycle, since it affects termination. o-valent R1 1-valent T0 o-valent T1 1-valent Actions 0 and 1 from T must be taken by the same process p. Why?

Proof of FLP (continued) Assume shared memory communication. Also assume that p q. Various cases are possible 1-valent Case 1. q writes e1 Decision 1 T1 ? T p reads T0 0-valent Decision 0 e0 Such a computation must exist since p can crash at any time Starting from T, let e1 be a computation that excludes any step by p. Let p crash after reading. Then e1 is a valid computation from T0 too. To all non-faulty processes, these two computations are identical, but the outcomes are different! This is not possible! But then, starting from a 0-valent state, a computation reaches decision 1 which is not feasible

Proof (continued) Case 2. 1-valent T1 q writes e1 Decision 1 T p writes T0 0-valent Decision 0 e0 Both write on the same variable, and p writes first. From T, let e1 be a computation that excludes any step by p. Let p crash after writing. Process q’s writing will overwrite it. Therefore e1 is a valid computation from T0 too. To all non-faulty processes, these two computations are identical, (q overwrites the value written by p) but the outcomes are different!

Proof (continued) Case 3 1-valent q writes T1 p writes Decision 1 Z T p writes T0 0-valent Let both p and q write, but q writes Decision 0 on different variables. Then regardless of the order of these writes, both computations lead to the same intermediate global state Z, which must be univalent. Is Z 1-valent or 0-valent? Both are absurd.

Proof (continued) Similar arguments can be made for communication using the message passing model too (See Nancy Lynch’s book). These lead to the fact that p, q cannot be distinct processes, and p q. Call p the decider process. What if p crashes in state T? No consensus is reached!

Conclusion In a purely asynchronous system, there is no solution to the consensus problem if a single process crashes. Note that this is true for deterministic algorithms only. Solutions do exist for the consensus problem using randomized algorithm, or using the synchronous model.

Consensus in Synchronous Systems: Byzantine Generals Problem Describes and solves the consensus problem on the synchronous model of communication. Processor speeds have lower bounds and communication delays have upper bounds. - The network is completely connected - Processes undergo byzantine failures, the worst possible kind of failure

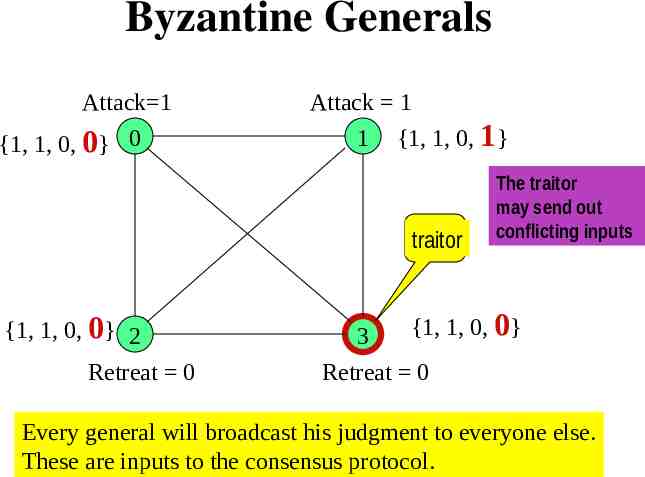
Byzantine Generals Problem n generals {0, 1, 2, ., n-1} decide about whether to "attack" or to "retreat" during a particular phase of a war. The goal is to agree upon the same plan of action. Some generals may be "traitors" and therefore send either no input, or send conflicting inputs to prevent the "loyal" generals from reaching an agreement. Devise a strategy, by which every loyal general eventually agrees upon the same plan, regardless of the action of the traitors.

Byzantine Generals Attack 1 {1, 1, 0, 0} 0 Attack 1 1 {1, 1, 0, 1} traitor {1, 1, 0, 0} 2 Retreat 0 3 The traitor may send out conflicting inputs {1, 1, 0, 0} Retreat 0 Every general will broadcast his judgment to everyone else. These are inputs to the consensus protocol.

Byzantine Generals We need to devise a protocol so that every peer (call it a lieutenant) receives the same value from any given general (call it a commander). Clearly, the lieutenants will have to use secondary information. Note that the roles of the commander and the lieutenants will rotate among the generals.

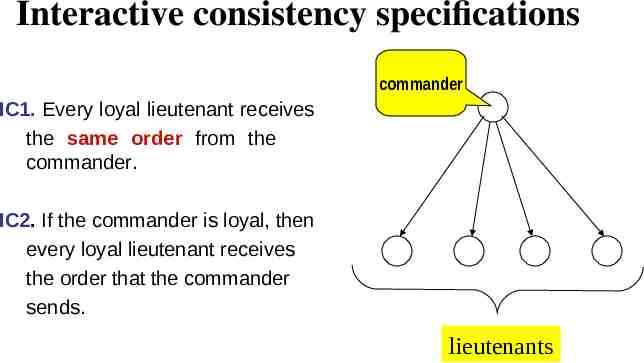
Interactive consistency specifications commander IC1. Every loyal lieutenant receives the same order from the commander. IC2. If the commander is loyal, then every loyal lieutenant receives the order that the commander sends. lieutenants

The Communication Model Oral Messages 1. Messages are not corrupted in transit. 2. Messages can be lost, but the absence of message can be detected. 3. When a message is received (or its absence is detected), the receiver knows the identity of the sender (or the defaulter). OM(m) represents an interactive consistency protocol in presence of at most m traitors.

An Impossibility Result Using oral messages, no solution to the Byzantine Generals problem exists with three or fewer generals and one traitor. Consider the two cases: commander 0 commander 0 1 0 1 1 0 0 1 lieutenent 1 lieutenant 2 (a) lieutenent 1 lieutenant 2 (b) In (a), to satisfy IC2, lieutenant 1 must trust the commander, but in IC2, the same idea leads to the violation of IC1.

Impossibility result Using oral messages, no solution to the Byzantine Generals problem exists with 3m or fewer generals and m traitors (m 0). The proof is by contradiction. Assume that such a solution exists. Now, divide the 3m generals into three groups of m generals each, such that all the traitors belong to one group. Let one general simulate each of these three groups. This scenario is equivalent to the case of three generals and one traitor. We already know that such a solution does not exist. Note. In the original paper, Lamport asks readers to be always suspicious about such an informal reasoning.

The OM(m) algorithm Recursive algorithm OM(m) OM(m-1) OM(m-2) OM(0) OM(0) Direct broadcast OM(0)

The OM(m) algorithm 1. Commander i sends out a value v (0 or 1) 2. If m 0, then every lieutenant j i, after receiving v, acts as a commander and initiates OM(m-1) with everyone except i . 3. Every lieutenant, collects (n-1) values: (n-2) values received from the lieutenants using OM(m-1), and one direct value from the commander. Then he picks the majority of these values as the order from i

Example of OM(1) commander commander 0 0 1 1 1 1 1 0 2 2 1 3 1 2 2 3 0 1 1 1 1 0 1 1 1 0 0 1 3 2 3 1 1 2 3 2 (a) 3 1 (b) 1 2

Example of OM(2) Commander OM(2) OM(2) 0 v v 1 v 2 v v 3 v 4 6 5 OM(1) v 4 v 5 6 v OM(0) v 5 v 6 v 6 v v v v v v OM(1) v 5 2 v v v 2 2 v 6 6 2 4 OM(0) v 2 4 5 5

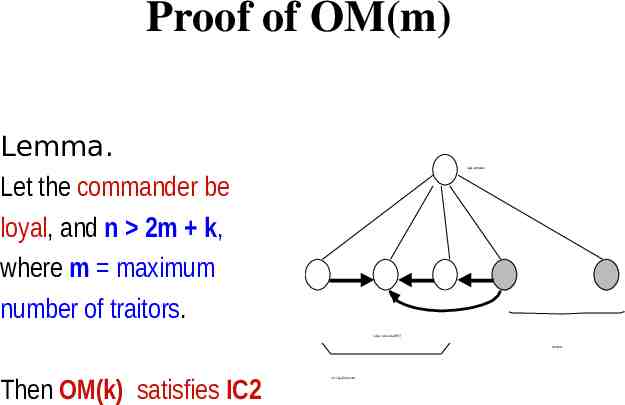
Proof of OM(m) Lemma. Let the commander be loyal, and n 2m k, where m maximum number of traitors. loyal commander values received via OM(r) m traitors Then OM(k) satisfies IC2 n-m-1 loyal lieutenants

Proof of OM(m) Proof If k 0, then the result trivially holds. loyal commander Let it hold for k r (r 0) i.e. OM(r) satisfies IC2. We have to show that it holds for k r 1 too. By definition n 2m r 1, so n-1 2m r So OM(r) holds for the lieutenants in the bottom row. Each loyal lieutenant collects n-m-1 identical good values and m bad values. So bad values are voted out (n-m-1 m r implies n-m-1 m) values received via OM(r) m traitors n-m-1 loyal lieutenants “OM(r) holds” means each loyal lieutenant receives identical values from every loyal commander

The final theorem Theorem. If n 3m where m is the maximum number of traitors, then OM(m) satisfies both IC1 and IC2. Proof. Consider two cases: Case 1. Commander is loyal. The theorem follows from the previous lemma (substitute k m). Case 2. Commander is a traitor. We prove it by induction. Base case. m 0 trivial. (Induction hypothesis) Let the theorem hold for m r. We have to show that it holds for m r 1 too.

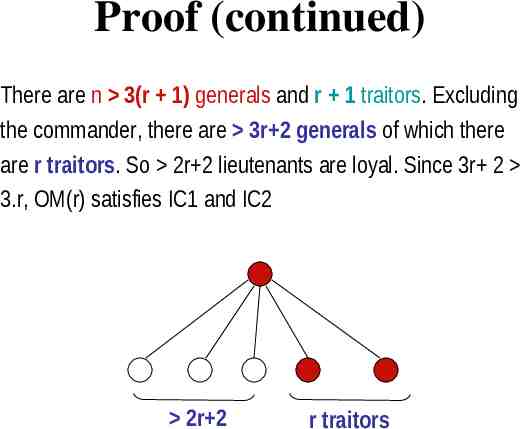
Proof (continued) There are n 3(r 1) generals and r 1 traitors. Excluding the commander, there are 3r 2 generals of which there are r traitors. So 2r 2 lieutenants are loyal. Since 3r 2 3.r, OM(r) satisfies IC1 and IC2 2r 2 r traitors

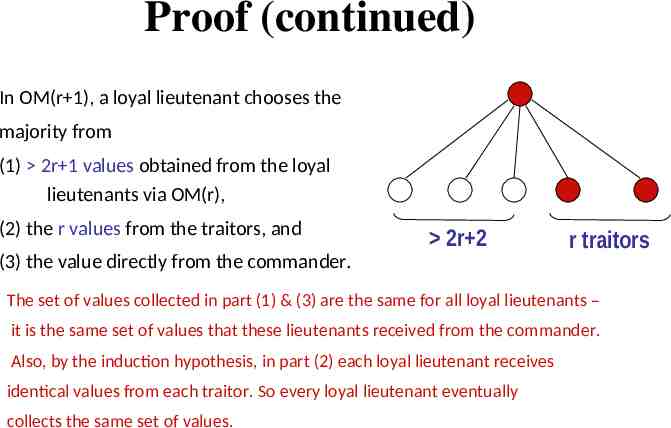
Proof (continued) In OM(r 1), a loyal lieutenant chooses the majority from (1) 2r 1 values obtained from the loyal lieutenants via OM(r), (2) the r values from the traitors, and 2r 2 r traitors (3) the value directly from the commander. The set of values collected in part (1) & (3) are the same for all loyal lieutenants – it is the same set of values that these lieutenants received from the commander. Also, by the induction hypothesis, in part (2) each loyal lieutenant receives identical values from each traitor. So every loyal lieutenant eventually collects the same set of values.