Detecting GRB ν’s – an Opportunity For Observing Lorentz

Detecting GRB ν’s – an Opportunity For Observing Lorentz Invariance Violation Uri Jacob and Tsvi Piran The Hebrew University Jerusalem, Israel ν γ

A possible violation of Lorentz invariance? Several quantum-gravity theories predict the break of the Lorentz symmetry when approaching the Planck mass scale c / G 1.22 1028 eV . Despite the great affection for the Lorentz symmetry, it is a viable possibility that this is only an approximate symmetry. There may exist a more complete accurate symmetry of nature for which the Lorentz symmetry emerges as a very good

An incentive: Lorentz invariance violation may resolve experimental paradoxes Further motivation for investigating a possible Further motivation for investigating a possible deformation of the Lorentz symmetry is achieved by considering certain astrophysical observations. Observations at Earth of Ultra High Energy Cosmic Rays and to a lesser extent of multi TeV photons may present a paradox with standard physics. It has been suggested in several works that a violation of Lorentz invariance could explain these issues. Remarkably, this is the only mechanism found to resolve both apparent paradoxes.

A phenomenological approach We consider here a simple phenomenological approach for Lorentz invariance deformation (LID) that can emerge as the low-energy expansion of some theory which predicts the break of Lorentz symmetry at very high energies. With the Planck-scale motivation we write the symmetry breaking energy scale as ξEpl. The leading order approximation for the deformed dispersion relation is expected n to 2 the2 form: 2 2 4 2 E take E p c m c E E pl

Validating or constraining the new theories We would like to obtain observational evidence or limits for the possible deviation from Lorentz symmetry. Astrophysical measurements allow us a reach of much higher energies than laboratories, and the cosmological time scales serve as amplifiers. Time-of-flight analyses of observational data from γ-ray bursts and other energetic photon sources, searching for energy dependant particle speeds that the LID phenomenology implies, were conducted by several groups over the last few years.

Current status No LID-induced time delays have yet been observed. Hence we have lower bounds on the symmetry breaking scale – for the two favored scenarios: n 1: ξ1 0.01 n 2: ξ2 10-9

Our aim: opening a new window with highly energetic GRBGRBνmodels ’s predict the The generally accepted production of high energy neutrinos alongside the γ-rays. The intensity and spectrum of these neutrinos are somewhat dependant on GRB model parameters, but at least a few GRB ν’s of 100 TeV and above are expected to be detected per year in a km3–scale detector (such as is currently being constructed). These neutrinos have energies many orders of magnitude higher than the observed burst photons and can open a new window in the examinable LID parameter space.

GRB ν’s LID delay Neutrino masses have a negligible effect on flight times – we can treat neutrinos as massless particles. The delay of a neutrino of observed energy E relative to a low energy photon, both emitted at redshift z isz given by: n 1 1 n E dz ' n t 1 z' 1 z' 3 H 0 0 2 E pl m For example, if the LID parameters are n 1, ξ 1 then a 100 TeV ν coming from a z 1 burst will arrive with a 4048 sec delay (with standard cosmological parameters).

wi Identifying GRB ν’s from noise Supposing a detection of ν’s with LID delays, we are left with the concern of identifying them as originating from GRBs – distinguishing the signal from noise. The most dominant background to the GRB ν signal consists of muons from atmospheric neutrinos. This noise is decreased greatly by observing only in the relevant energy, time and angular windows. The atmospheric ν spectrum is approximately given by: dN atm 13 5 10 E / 100TeV [100TeV] -1cm -2 sec -1sr -1 dE with β 3.7 for Eν 100 TeV and β 4 for Eν 100 TeV. Knowing the cross section for ν interactions in the detector, we calculate the number of background events.

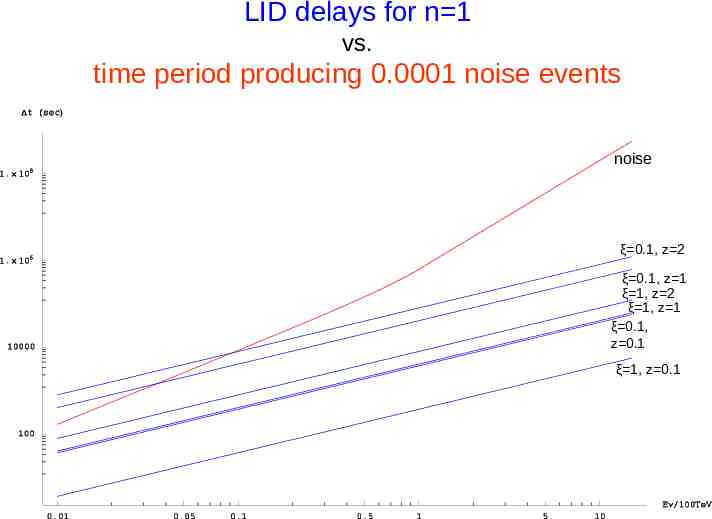
LID delays for n 1 vs. time period producing 0.0001 noise events noise ξ 0.1, z 2 ξ 0.1, z 1 ξ 1, z 2 ξ 1, z 1 ξ 0.1, z 0.1 ξ 1, z 0.1

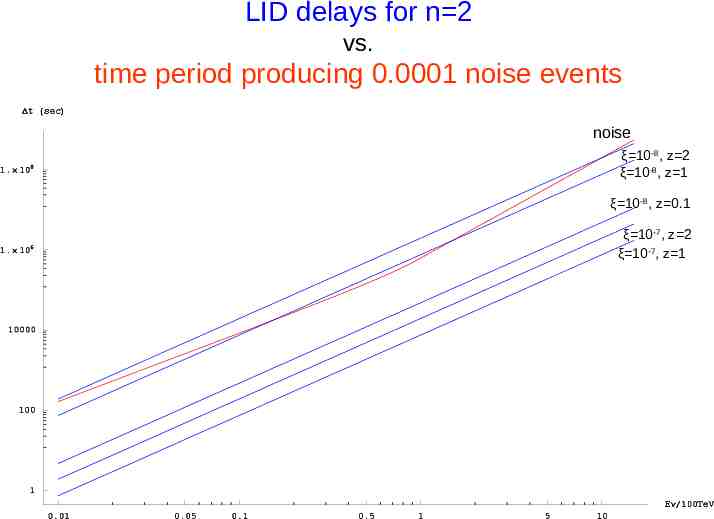
LID delays for n 2 vs. time period producing 0.0001 noise events noise ξ 10-8, z 2 ξ 10-8, z 1 ξ 10-8, z 0.1 ξ 10-7, z 2 ξ 10-7, z 1

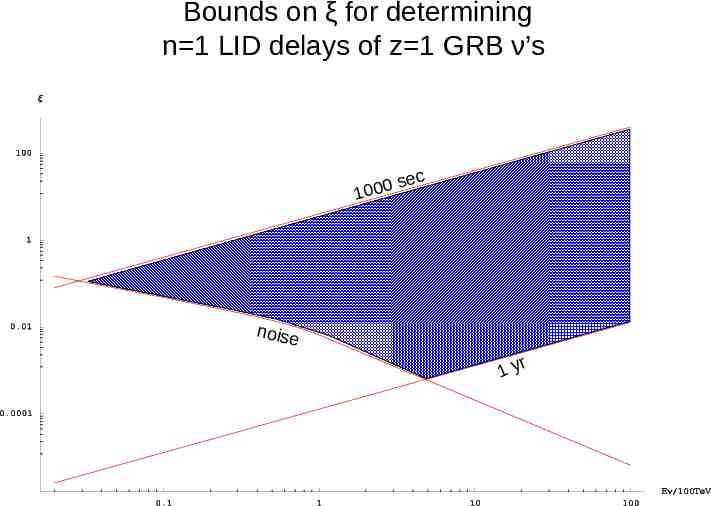
Bounds on ξ for determining n 1 LID delays of z 1 GRB ν’s sec 0 0 0 1 noise r 1y

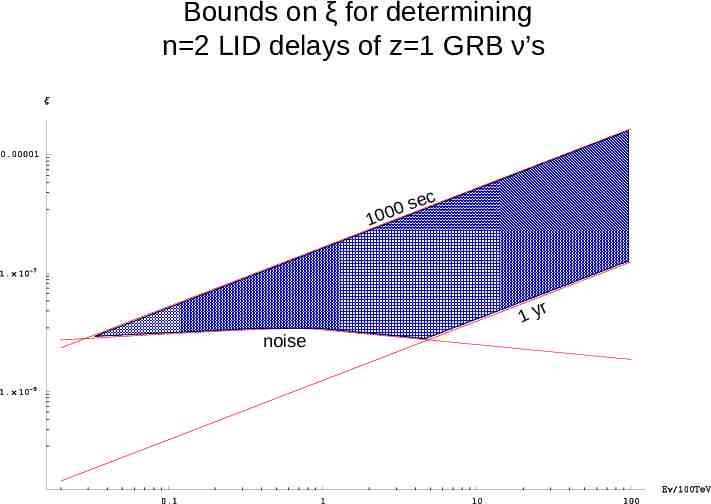
Bounds on ξ for determining n 2 LID delays of z 1 GRB ν’s ec s 0 100 r 1y noise

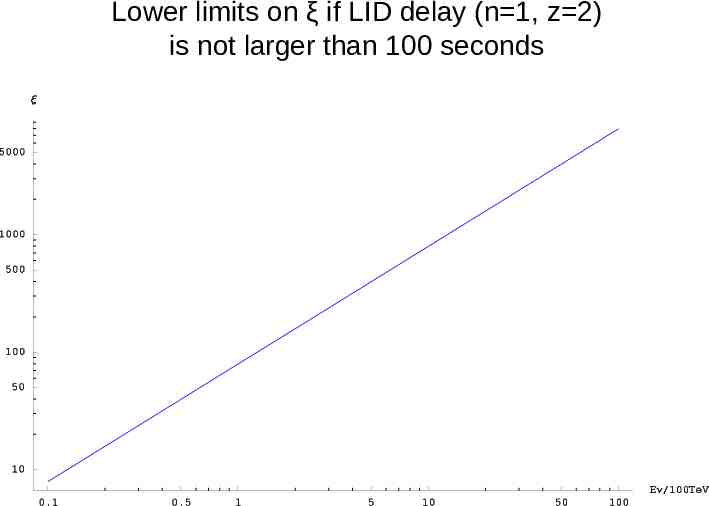
Lower limits on ξ if LID delay (n 1, z 2) is not larger than 100 seconds

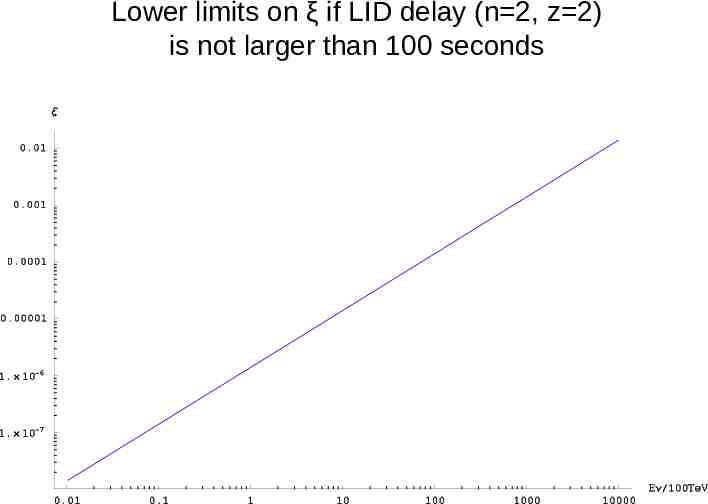
Lower limits on ξ if LID delay (n 2, z 2) is not larger than 100 seconds

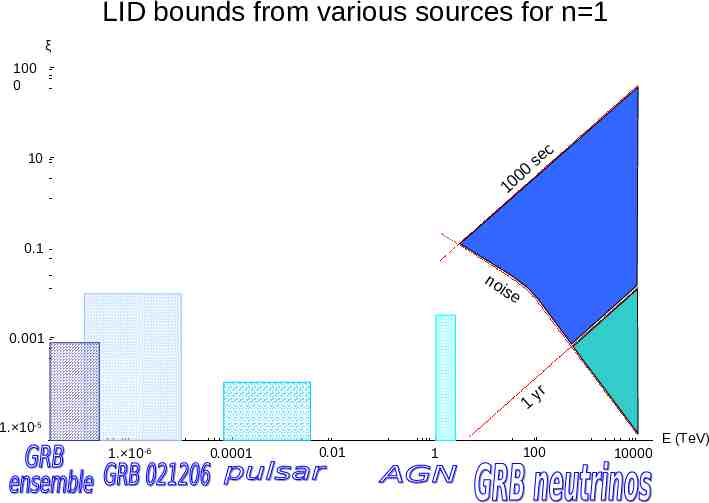
LID bounds from various sources for n 1 ξ 100 0 10 00 0 1 c se 0.1 no is e 0.001 1 yr 1. 10-5 1. 10 -6 0.0001 0.01 1 100 10000 E (TeV)

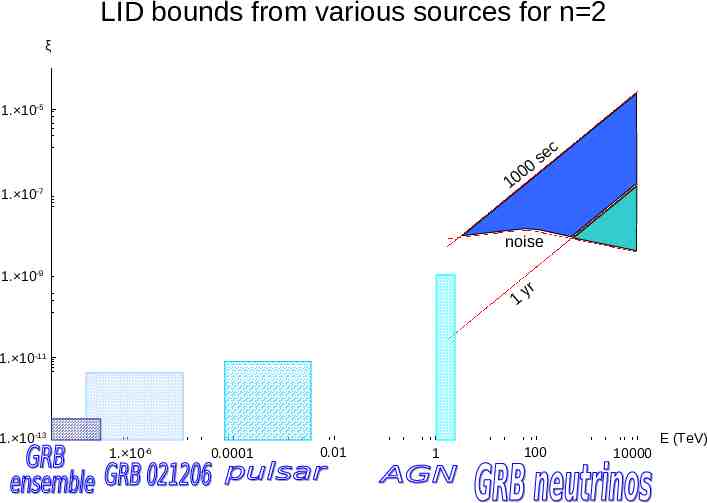
LID bounds from various sources for n 2 ξ 1. 10-5 0 10 1. 10-7 0 se c noise 1. 10-9 1 yr 1. 10-11 1. 10-13 1. 10 -6 0.0001 0.01 1 100 10000 E (TeV)

Summary Detecting and identifying high energy ν’s from GRBs is a practical plan for the near future. The arrival time of these ν’s can be compared to the observed γ-rays. The highly energetic ν’s can provide us insight on a LID parameter space that is hidden from other observation methods, probing much higher symmetry breaking scales. The prospects of determining LID or imposing very strict constraints on it using GRB ν’s appear excellent.