Data Mining for Complex Network Introduction and Background

Data Mining for Complex Network Introduction and Background

Welcome! Instructor: Ruoming Jin Homepage: www.cs.kent.edu/ jin/ Office: 264 MCS Building Email: [email protected]

Course overview The course goal First of all, this is a research course, or a special topic course. There is no textbook and even no definition what topics are supposed to under the course name Discussing the state-of-are techniques for mining complex networks Review & Course Project

Simple Concepts (Review) Erdős–Rényi model Random Graph Model Markov Chain and Random Walk Maximal Likelihood/Model Selection

Requirement Each of you will have one presentation Review Paper Select a topic and review at least four papers Bonus: Develop a new idea on this topic Course Project One or Two a group Collect data; preprocess data; analyzing the data; Final Grade: 30% presentations, 25% review, 35% project, and 10% class participation

What is a network? Network: a collection of entities that are interconnected with links. people that are friends computers that are interconnected web pages that point to each other proteins that interact

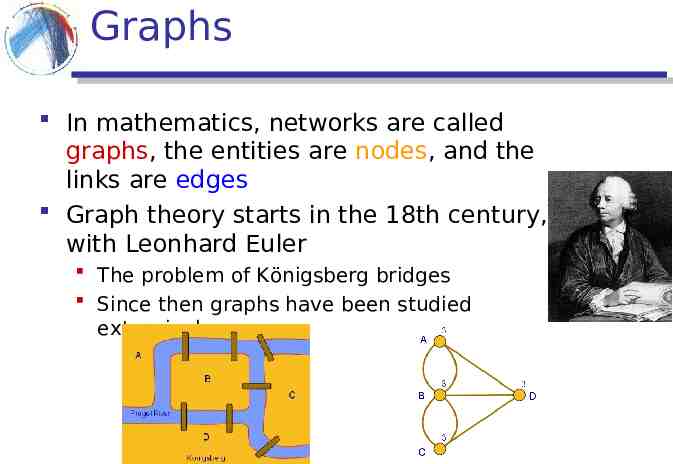
Graphs In mathematics, networks are called graphs, the entities are nodes, and the links are edges Graph theory starts in the 18th century, with Leonhard Euler The problem of Königsberg bridges Since then graphs have been studied extensively.

Networks in the past Graphs have been used in the past to model existing networks (e.g., networks of highways, social networks) usually these networks were small network can be studied visual inspection can reveal a lot of information

Networks now More and larger networks appear Products of technological advancement e.g., Internet, Web Result of our ability to collect more, better, and more complex data e.g., gene regulatory networks Networks of thousands, millions, or billions of nodes impossible to visualize

The internet map

Understanding large graphs What are the statistics of real life networks? Can we explain how the networks were generated? What else? A still very young field! (What is the basic principles and what those principle will mean?)

Measuring network properties Around 1999 Watts and Strogatz, Dynamics and small-world phenomenon Faloutsos3, On power-law relationships of the Internet Topology Kleinberg et al., The Web as a graph Barabasi and Albert, The emergence of scaling in real networks

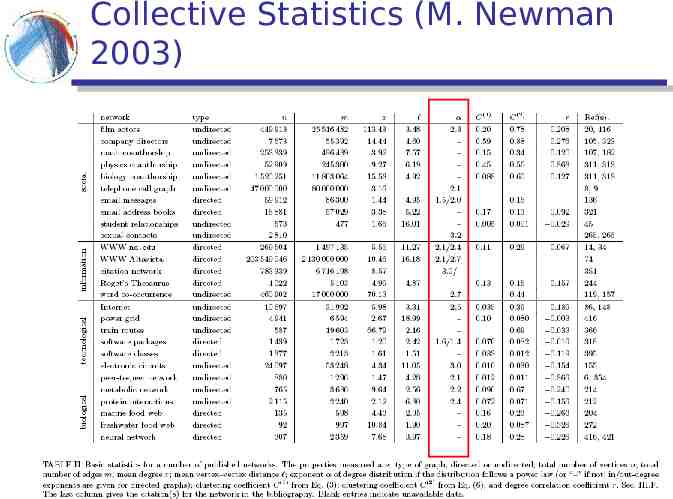
Real network properties Most nodes have only a small number of neighbors (degree), but there are some nodes with very high degree (power-law degree distribution) scale-free networks If a node x is connected to y and z, then y and z are likely to be connected high clustering coefficient Most nodes are just a few edges away on average. small world networks Networks from very diverse areas (from internet to biological networks) have similar properties Is it possible that there is a unifying underlying generative process?

Generating random graphs Classic graph theory model (Erdös-Renyi) each edge is generated independently with probability p Very well studied model but: most vertices have about the same degree the probability of two nodes being linked is independent of whether they share a neighbor the average paths are short

Modeling real networks Real life networks are not “random” Can we define a model that generates graphs with statistical properties similar to those in real life? a flurry of models for random graphs

Processes on networks Why is it important to understand the structure of networks? Epidemiology: Viruses propagate much faster in scale-free networks Vaccination of random nodes does not work, but targeted vaccination is very effective

The future of networks Networks seem to be here to stay More and more systems are modeled as networks Scientists from various disciplines are working on networks (physicists, computer scientists, mathematicians, biologists, sociologist, economists) There are many questions to understand.

Basic Mathematical Tools Graph theory Probability theory Linear Algebra

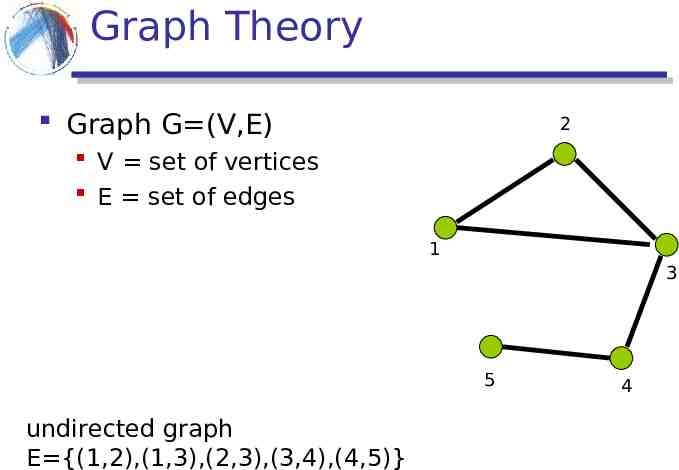
Graph Theory Graph G (V,E) 2 V set of vertices E set of edges 1 3 5 undirected graph E {(1,2),(1,3),(2,3),(3,4),(4,5)} 4

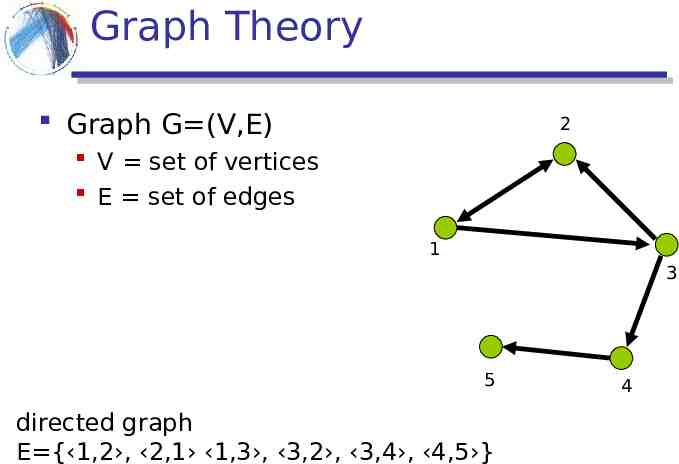
Graph Theory Graph G (V,E) 2 V set of vertices E set of edges 1 3 5 directed graph E {‹1,2›, ‹2,1› ‹1,3›, ‹3,2›, ‹3,4›, ‹4,5›} 4

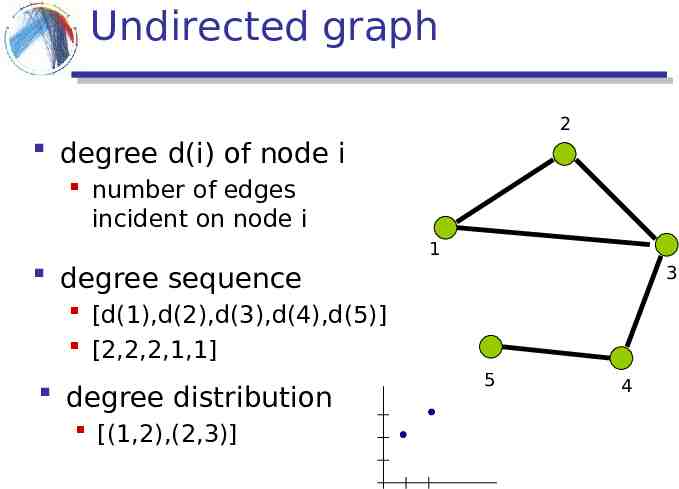
Undirected graph 2 degree d(i) of node i number of edges incident on node i 1 degree sequence 3 [d(1),d(2),d(3),d(4),d(5)] [2,2,2,1,1] degree distribution [(1,2),(2,3)] 5 4

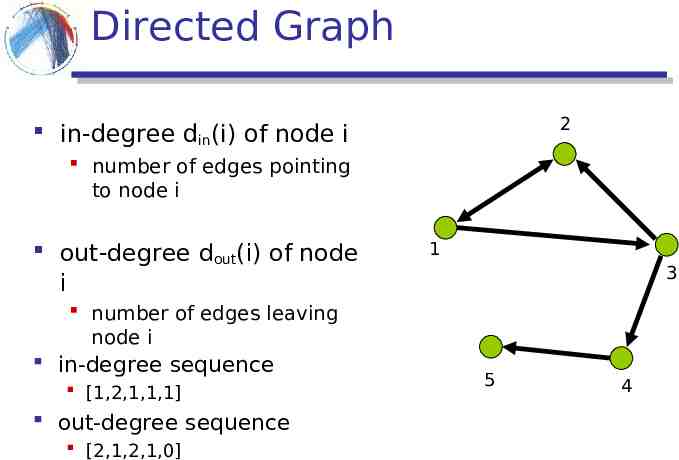
Directed Graph 2 in-degree din(i) of node i number of edges pointing to node i out-degree dout(i) of node i 1 3 number of edges leaving node i in-degree sequence [1,2,1,1,1] out-degree sequence [2,1,2,1,0] 5 4

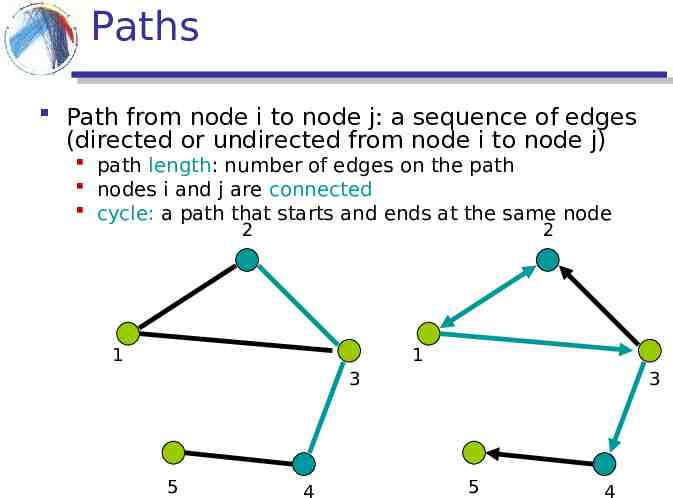
Paths Path from node i to node j: a sequence of edges (directed or undirected from node i to node j) path length: number of edges on the path nodes i and j are connected cycle: a path that starts and ends at the same node 2 2 1 1 3 5 4 3 5 4

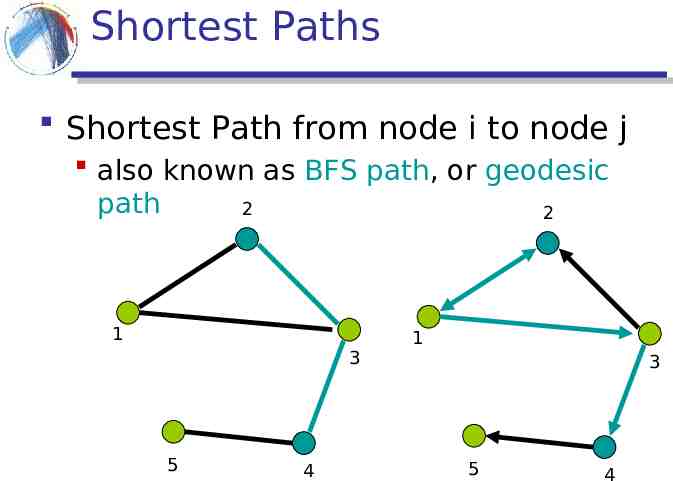
Shortest Paths Shortest Path from node i to node j also known as BFS path, or geodesic path 2 2 1 3 5 4 1 3 5 4

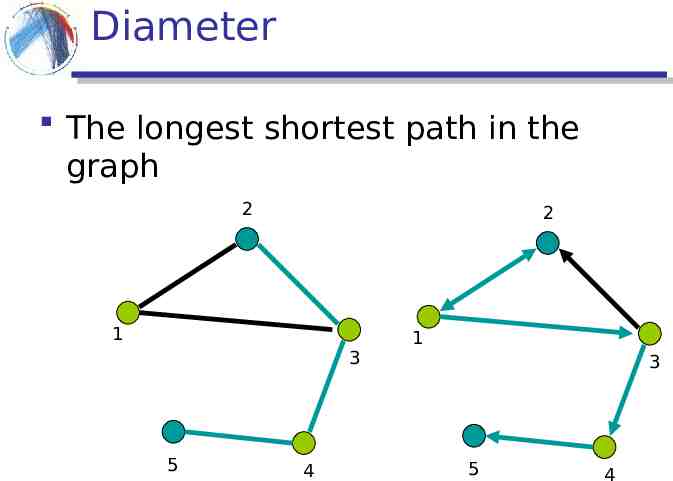
Diameter The longest shortest path in the graph 2 2 1 3 5 4 1 3 5 4

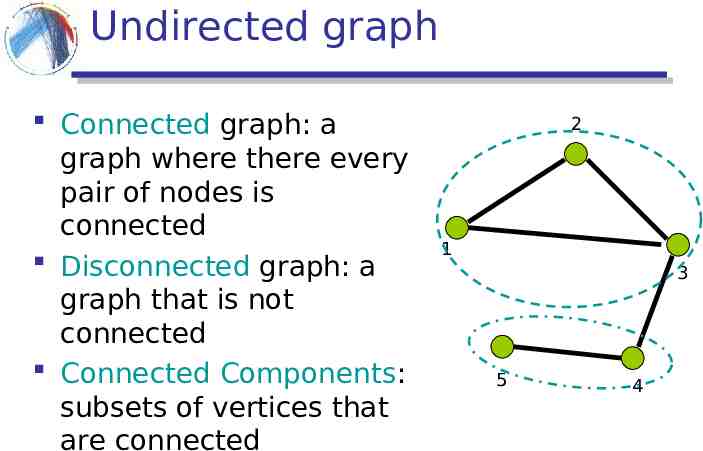
Undirected graph Connected graph: a graph where there every pair of nodes is connected Disconnected graph: a graph that is not connected Connected Components: subsets of vertices that are connected 2 1 3 5 4

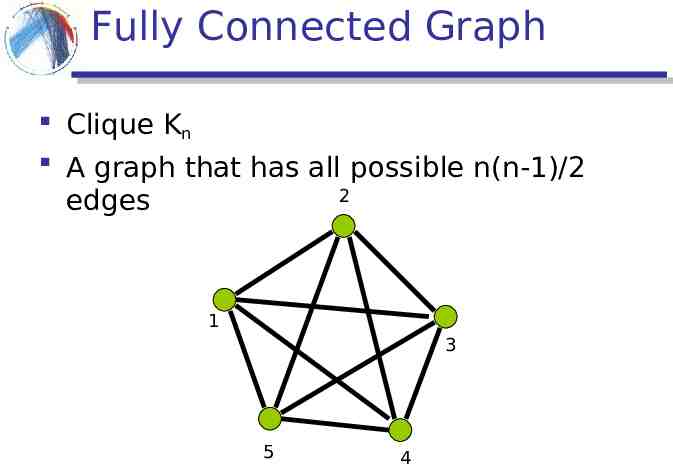
Fully Connected Graph Clique Kn A graph that has all possible n(n-1)/2 2 edges 1 3 5 4

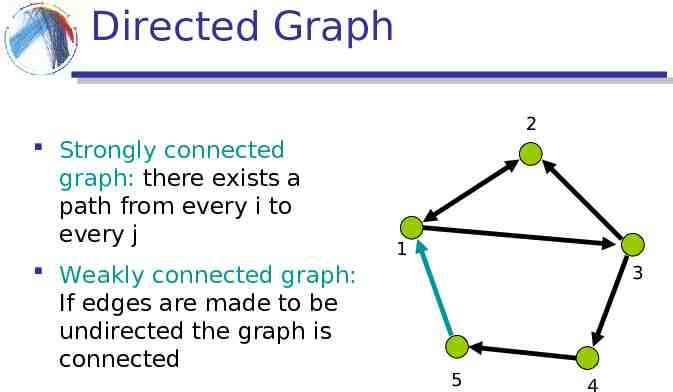
Directed Graph 2 Strongly connected graph: there exists a path from every i to every j Weakly connected graph: If edges are made to be undirected the graph is connected 1 3 5 4

Subgraphs Subgraph: Given V’ V, and E’ E, the graph G’ (V’,E’) is a subgraph of G. Induced subgraph: Given V’ V, let E’ E is the set of all edges between the nodes in V’. The graph G’ (V’,E’), is an induced subgraph of G 2 1 3 5 4

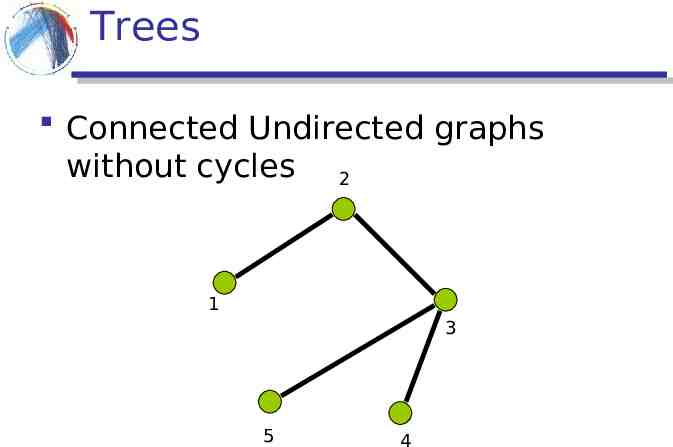
Trees Connected Undirected graphs without cycles 2 1 3 5 4

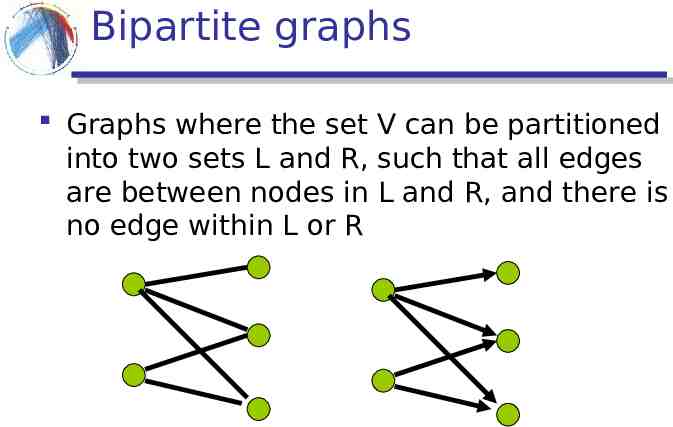
Bipartite graphs Graphs where the set V can be partitioned into two sets L and R, such that all edges are between nodes in L and R, and there is no edge within L or R

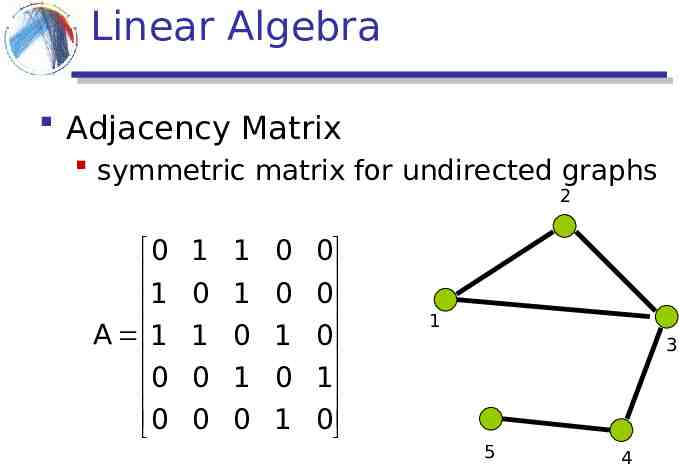
Linear Algebra Adjacency Matrix symmetric matrix for undirected graphs 2 0 1 A 1 0 0 1 1 0 0 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0 1 3 5 4

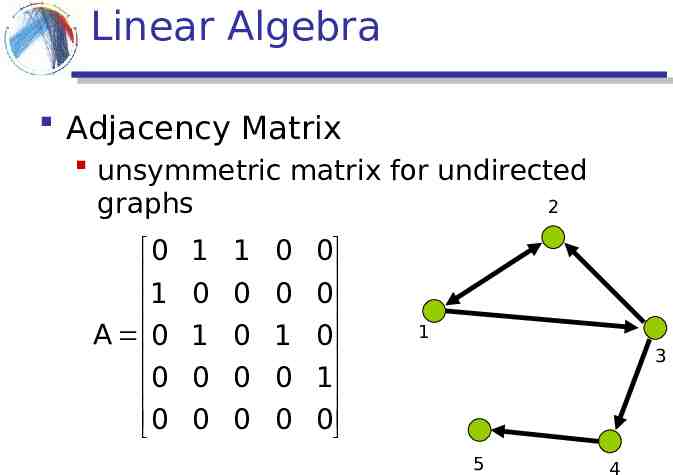
Linear Algebra Adjacency Matrix unsymmetric matrix for undirected graphs 2 0 1 A 0 0 0 1 1 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 1 3 5 4

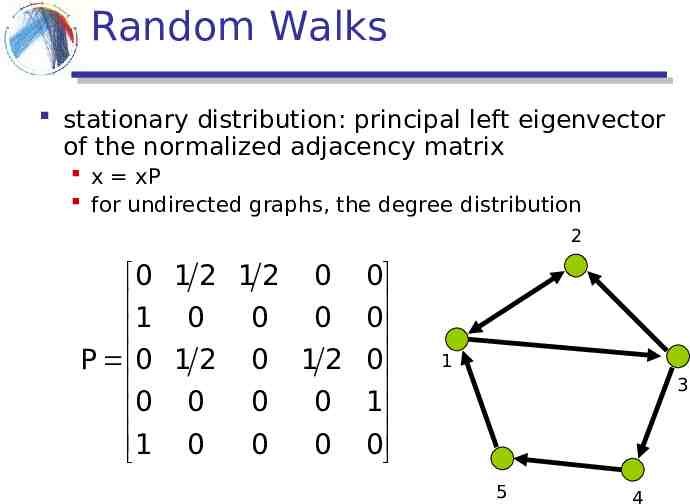
Random Walks Start from a node, and follow links uniformly at random. Stationary distribution: The fraction of times that you visit node i, as the number of steps of the random walk approaches infinity if the graph is strongly connected, the stationary distribution converges to a unique vector.

Random Walks stationary distribution: principal left eigenvector of the normalized adjacency matrix x xP for undirected graphs, the degree distribution 2 0 1 2 1 2 0 1 0 0 0 P 0 1 2 0 1 2 0 0 0 0 1 0 0 0 0 0 0 1 0 1 3 5 4

Eigenvalues and Eigenvectors The value λ is an eigenvalue of matrix A if there exists a non-zero vector x, such that Ax λx. Vector x is an eigenvector of matrix A The largest eigenvalue is called the principal eigenvalue The corresponding eigenvector is the principal eigenvector Corresponds to the direction of maximum change

Types of networks Social networks Knowledge (Information) networks Technology networks Biological networks

Social Networks Links denote a social interaction Networks of acquaintances actor networks co-authorship networks director networks phone-call networks e-mail networks IM networks Microsoft buddy network Bluetooth networks sexual networks home page networks

Knowledge (Information) Networks Nodes store information, links associate information Citation network (directed acyclic) The Web (directed) Peer-to-Peer networks Word networks Networks of Trust Bluetooth networks

Technological networks Networks built for distribution of commodity The Internet router level, AS level Power Grids Airline networks Telephone networks Transportation Networks roads, railways, pedestrian traffic Software graphs

Biological networks Biological systems represented as networks Protein-Protein Interaction Networks Gene regulation networks Metabolic pathways The Food Web Neural Networks

Now what? The world is full with networks. What do we do with them? understand their topology and measure their properties study their evolution and dynamics create realistic models create algorithms that make use of the network structure

Measuring Networks Degree distributions Small world phenomena Clustering Coefficient Mixing patterns Degree correlations Communities and clusters

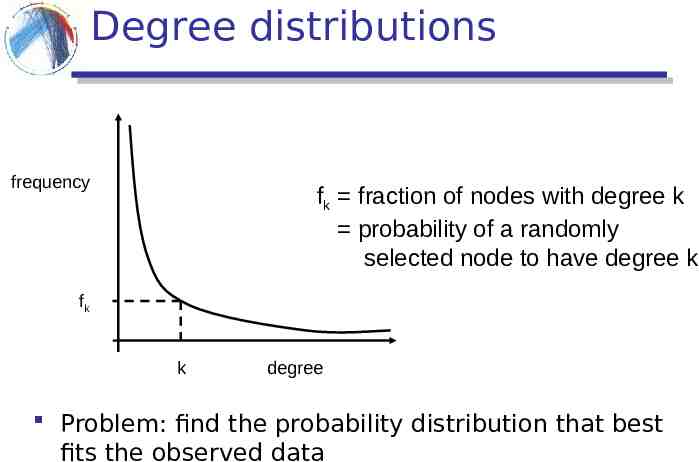
Degree distributions frequency fk fraction of nodes with degree k probability of a randomly selected node to have degree k fk k degree Problem: find the probability distribution that best fits the observed data

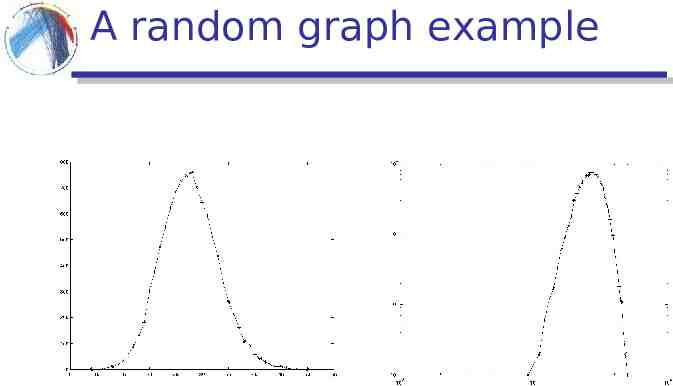
Power-law distributions The degree distributions of most real-life networks follow a power law p(k) Ck-α Right-skewed/Heavy-tail distribution there is a non-negligible fraction of nodes that has very high degree (hubs) scale-free: no characteristic scale, average is not informative In stark contrast with the random graph model! highly concentrated around the mean the probability of very high degree nodes is exponentially small

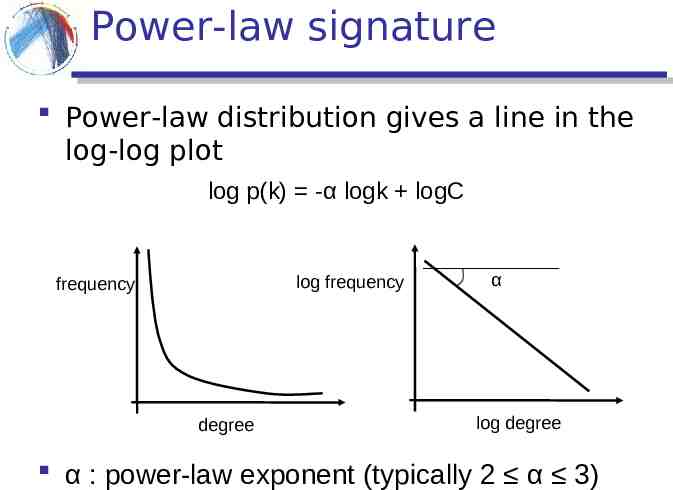
Power-law signature Power-law distribution gives a line in the log-log plot log p(k) -α logk logC log frequency frequency degree α log degree α : power-law exponent (typically 2 α 3)

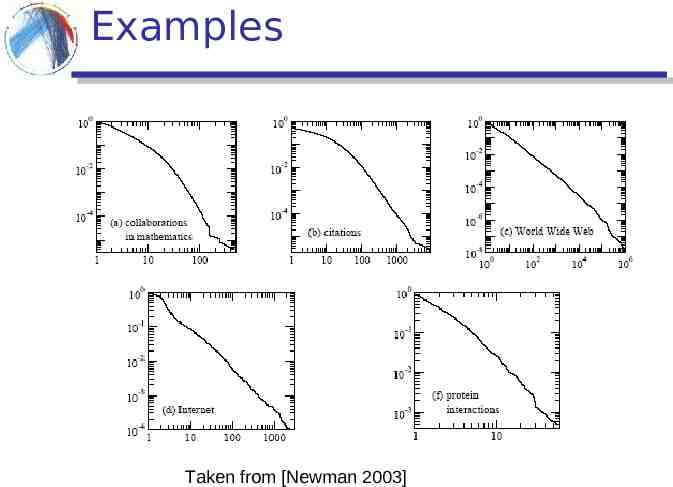
Examples Taken from [Newman 2003]

A random graph example

Maximum degree For random graphs, the maximum degree is highly concentrated around the average degree z For power law graphs 1/(α 1) kmax n Rough argument: solve nP[X k] 1

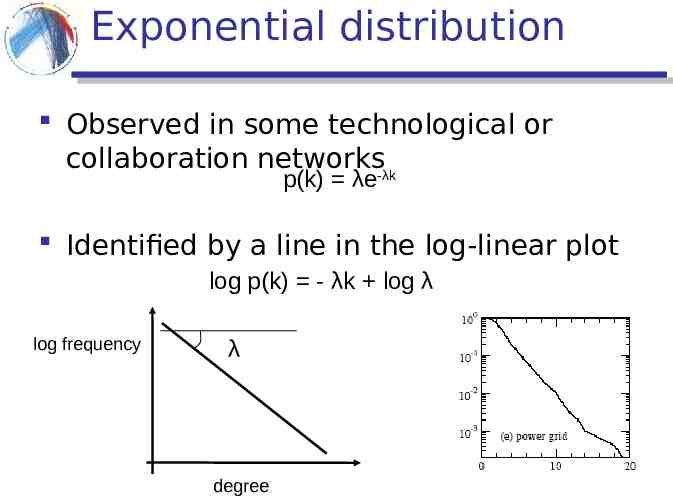
Exponential distribution Observed in some technological or collaboration networks-λk p(k) λe Identified by a line in the log-linear plot log p(k) - λk log λ log frequency λ degree

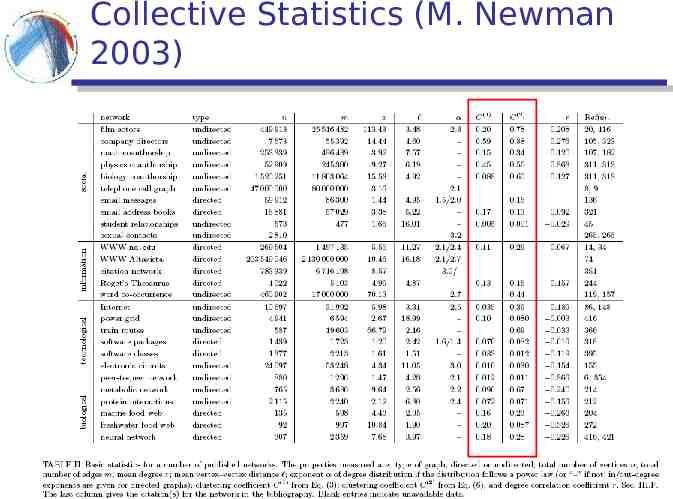
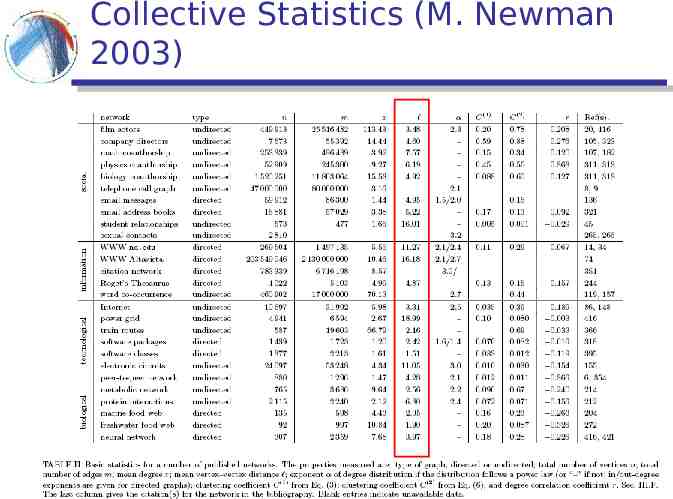
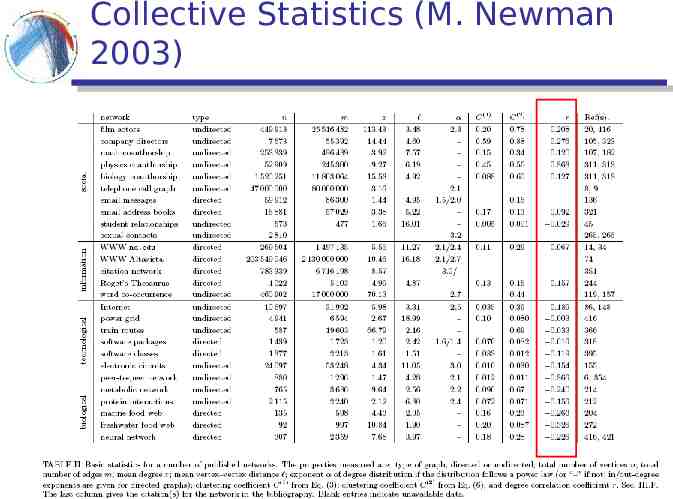
Collective Statistics (M. Newman 2003)

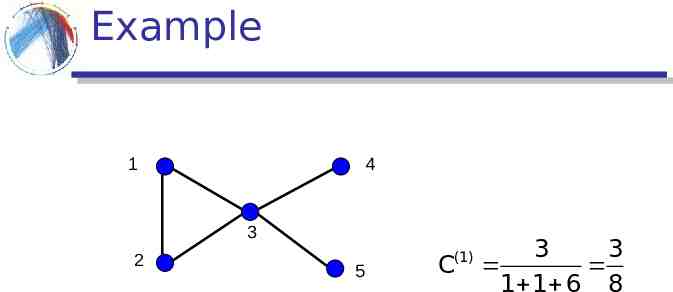
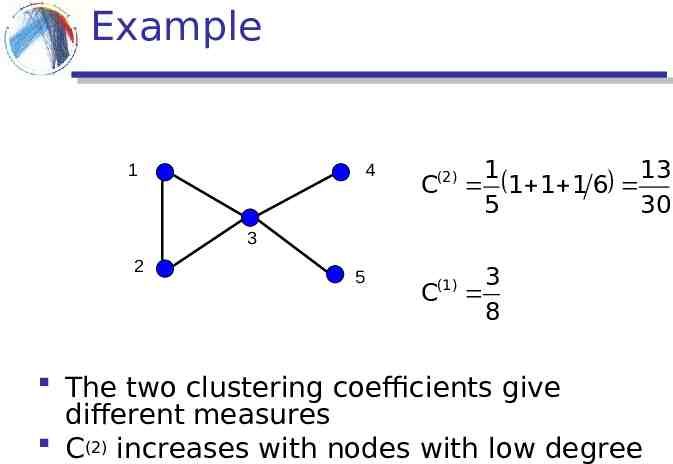
Clustering (Transitivity) coefficient Measures the density of triangles (local clusters) in the graph Two different ways to measure it: C(1) trianglescenteredat nodei triplescenteredat nodei i i The ratio of the means

Example 1 4 3 2 5 3 3 C(1) 1 1 6 8

Clustering (Transitivity) coefficient Clustering coefficient for node i trianglescenteredat nodei Ci triplescenteredat nodei (2) C 1 Ci n The mean of the ratios

Example 1 4 (2) C 1 13 1 1 1 6 5 30 3 2 5 C(1) 3 8 The two clustering coefficients give different measures C(2) increases with nodes with low degree

Collective Statistics (M. Newman 2003)

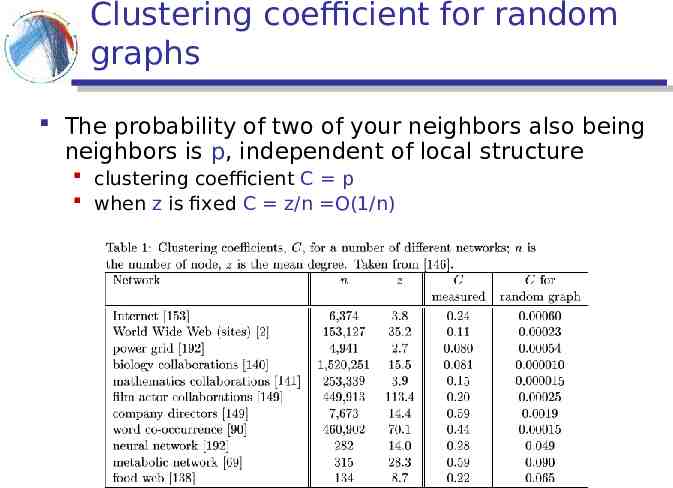
Clustering coefficient for random graphs The probability of two of your neighbors also being neighbors is p, independent of local structure clustering coefficient C p when z is fixed C z/n O(1/n)

Small world phenomena Small worlds: networks with short paths Stanley Milgram (1933-1984): “The man who shocked the world” Obedience to authority (1963) Small world experiment (1967)

Small world experiment Letters were handed out to people in Nebraska to be sent to a target in Boston People were instructed to pass on the letters to someone they knew on first-name basis The letters that reached the destination followed paths of length around 6 Six degrees of separation: (play of John Guare) Also: The Kevin Bacon game The Erdös number Small world project: http://smallworld.columbia.edu/index.html

Measuring the small world phenomenon dij shortest path between i and j Diameter: d maxdij i,j Characteristic path length: 1 dij n(n- 1)/2 i j Harmonic mean 1 -1 dij n(n- 1)/2 i j 1

Collective Statistics (M. Newman 2003)

Mixing patterns Assume that we have various types of nodes. What is the probability that two nodes of different type are linked? assortative mixing (homophily) E : mixing matrix p(i,j) mixing probability p(i,j) E(i, j) E(i,j) i,j p(j i) conditional mixing probability p(j i) E(i, j) E(i,j) j

Mixing coefficient Gupta, Anderson, May 1989 p(i i) - 1 Q i N 1 Advantages: Q 1 if the matrix is diagonal Q 0 if the matrix is uniform Disadvantages sensitive to transposition does not weight the entries

Mixing coefficient Newman 2003 a(i) p(i,j) (row marginal) b(i) p(j,i) (column marginal) j j p(i i) - a(i)b(i) r 1 a(i)b(i) i i i Advantages: r 0.621 Q 0.528 r 1 for diagonal matrix , r 0 for uniform matrix not sensitive to transposition, accounts for weighting

Degree correlations Do high degree nodes tend to link to high degree nodes? Pastor Satoras et al. plot the mean degree of the neighbors as a function of the degree Newman compute the correlation coefficient of the degrees of the two endpoints of an edge assortative/disassortative

Collective Statistics (M. Newman 2003)

Communities and Clusters Use the graph structure to discover communities of nodes essentially clustering and classification on graphs

Other measures Frequent (or interesting) motifs bipartite cliques in the web graph patterns in biological and software graphs Use graphlets to compare models [Przulj,Corneil,Jurisica 2004]

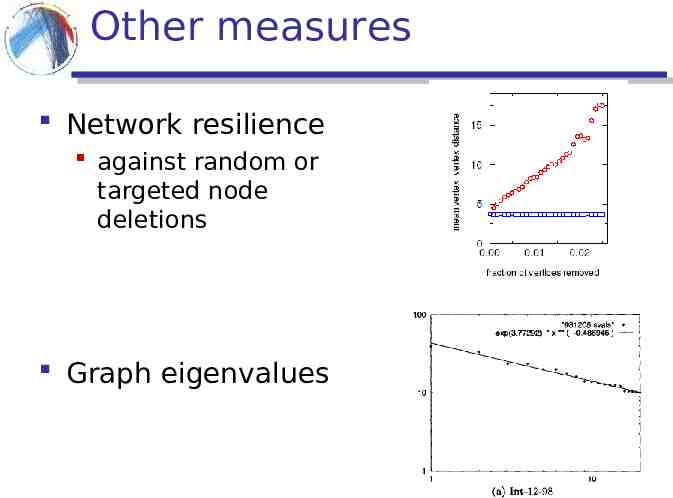
Other measures Network resilience against random or targeted node deletions Graph eigenvalues

Other measures The giant component Other?

References M. E. J. Newman, The structure and function of complex networks, SIAM Reviews, 45(2): 167-256, 2003 M. E. J. Newman, Random graphs as models of networks in Handbook of Graphs and Networks, S. Bornholdt and H. G. Schuster (eds.), Wiley-VCH, Berlin (2003). N. Alon J. Spencer, The Probabilistic Method