CSE 5245 Lecture 1 Srinivasan Parthasarathy Ack: Slides are

CSE 5245 Lecture 1 Srinivasan Parthasarathy Ack: Slides are adapted from Ymir Vigfusson; who in turn inherited them from various sources – as noted in individual slides. Many of the images are adapted from the textbook(s) for the course.

Networks & Complex Systems We are surrounded by hopelessly complex systems: Society is a collection of seven billion individuals Communication systems link electronic devices Information and knowledge is organized and linked Thousands of genes in our cells work together in a seamless fashion Our thoughts are hidden in the connections between billions of neurons in our brain These systems, random looking at first, display signatures of order and self-organization 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 2

Networks Each such system can be represented as a network, that defines the interactions between the components 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 3

Networks: Communication Graph of the Internet (Autonomous Systems) 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 4

Networks: Information Connections between political blogs 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 5

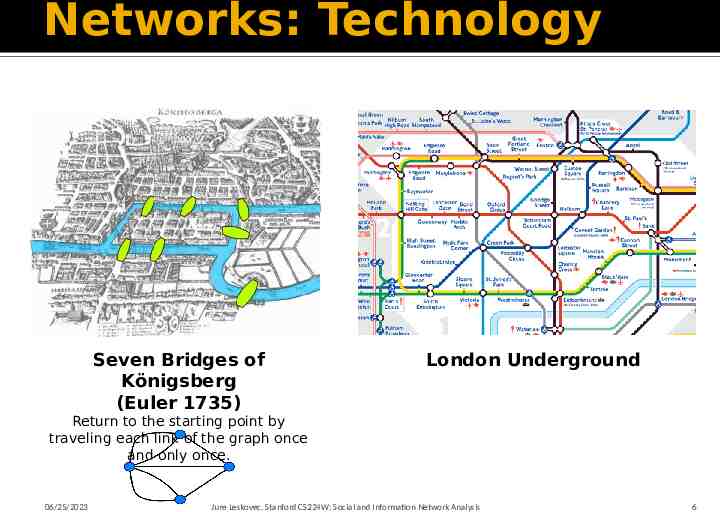
Networks: Technology Seven Bridges of Königsberg (Euler 1735) London Underground Return to the starting point by traveling each link of the graph once and only once. 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 6

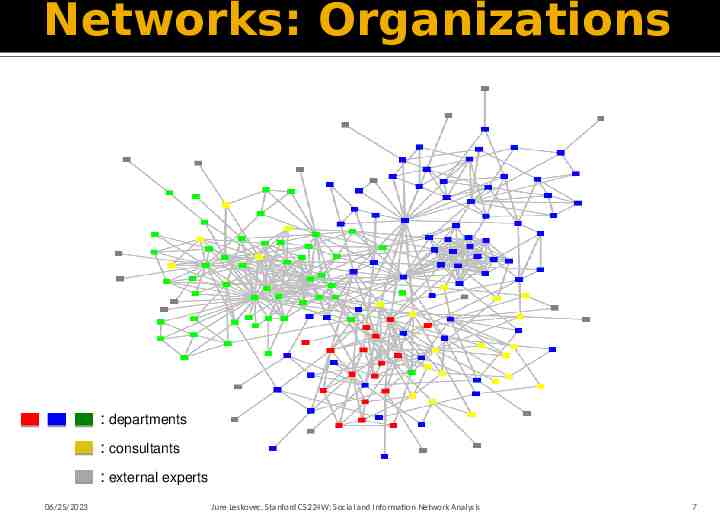
Networks: Organizations : departments : consultants : external experts 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 7

Networks: Brain 06/25/2023 Human brain has between 10-100 billion neurons Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 8

Networks: Cells Protein-Protein Interaction Networks: Metabolic networks: Nodes: Proteins Nodes: Metabolites and enzymes Edges: ‘physical’ interactions Edges: Chemical reactions 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 9

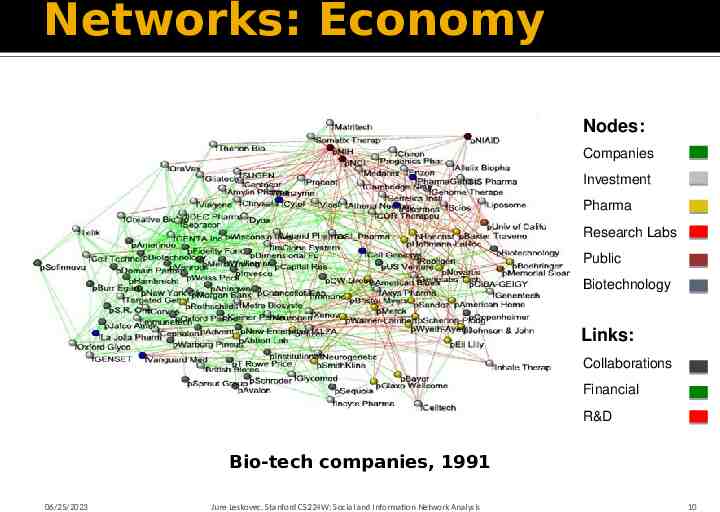
Networks: Economy Nodes: Companies Investment Pharma Research Labs Public Biotechnology Links: Collaborations Financial R&D Bio-tech companies, 1991 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 10

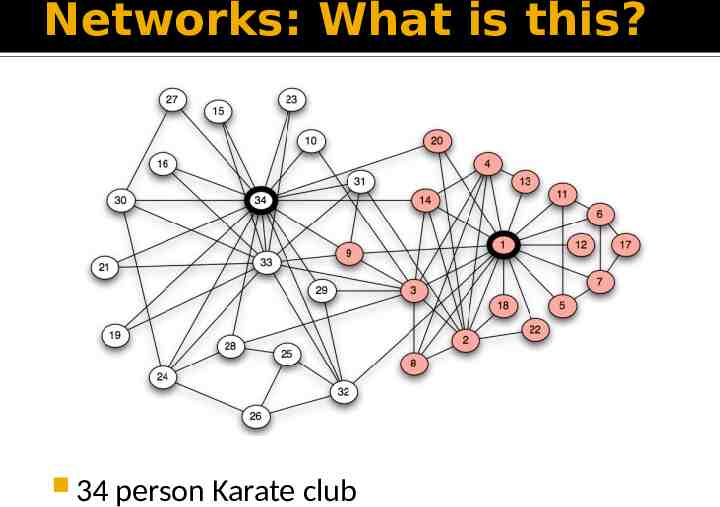
Networks: What is this? 34 person Karate club

Networks: What about this? E-mail communication patterns within HP Superimposed on the company hierarchy

Networks are everywhere Modern society is “connected“ in different ways Global communication The Internet Social networks Financial systems News and media Network science “The study of phenomena that take place within complex social, economic and technological systems.“

Why Networks? Behind each such system there is an intricate wiring diagram, a network, that defines the interactions between the components The key to understanding these complex systems unless is to understand the networks behind them 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 14

Reasoning about networks What do we hope to achieve from studying networks? Patterns and statistical properties of network data Design principles and models Understand why networks are organized the way they are Predict behavior of networked systems How do we reason about networks? Empirical: Study network data to find organizational principles Mathematical models: Probabilistic, graph theory Algorithms for analyzing graphs 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 15

Networks: Structure & Process What do we study in networks? Structure and evolution What is the structure of a network? Why and how did it became to have such structure? Processes and dynamics Networks provide a “skeleton” for spreading of information, behavior, diseases How do information and diseases spread? 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 16

Specific questions What are the structural features of networks? Hard to eyeball features of large networks Can we reason about behavior and interaction in networks? Strategic incentives, cause-and-effect relationships What are the dynamics of aggregate behavior? Why are YouTube and Facebook so popular? How do things go viral? How do diseases spread?

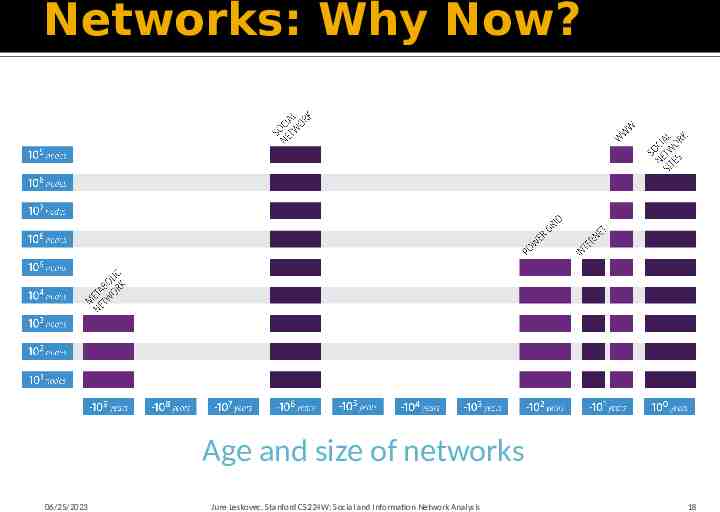
Networks: Why Now? Age and size of networks 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 18

Why Networks? Why Now? The role of networks is expanding Data availability Rise of the Web 2.0 and Social media Universality Networks from various domains of science, nature, and technology are more similar than one would expect Shared vocabulary between fields Computer Science, Social Sciences, Physics, Economics, Statistics, Biology, Political Science 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 19

Networks: Impact 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 20

Networks: Impact Intelligence and fighting (cyber) terrorism 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 21

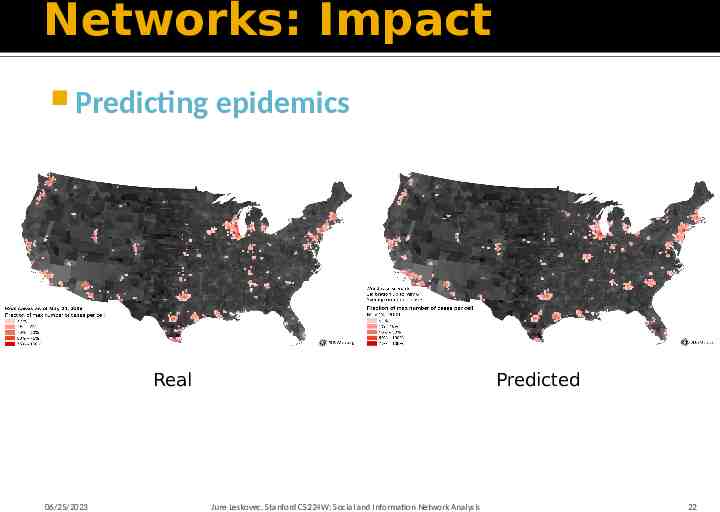
Networks: Impact Predicting epidemics Real 06/25/2023 Predicted Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 22

Networks: Impact Interactions of human disease Drug design 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 23

COURSE LOGISTICS

Logistics Tu/Th Office 2:20-3:40PM hours: Srini: TH 1-2 PM, and by appointment on Fridays. Yu Wang: T 1-2 PM, Wed 11-12 (noon), Mondays by apt. Prerequisites (these would be helpful) Linear Algebra Probability and statistics Graph Theory Databases Data Mining

Logistics Reference material Networks, Crowds and Markets (Easley, Kleinberg 2010). Book also available online! Networks an Introduction (M. Newman). Also available online for free from an OSU IP address. Website http://www.cse.ohio-state.edu/ srini/5245 Collaboration advised and encouraged! You are expected to maintain academic integrity and the OSU honor code

Evaluation (tentative and subject to change) Problem Sets/Assignments (35%) Midterm (25%) Team Project and Presentation (40%) Give an enthusiastic, well-prepared talk on the key ideas in chosen scientific papers on the topics of the course Team projects (at least 3 members) Teams must comprise of at least one grad and one undergraduate student

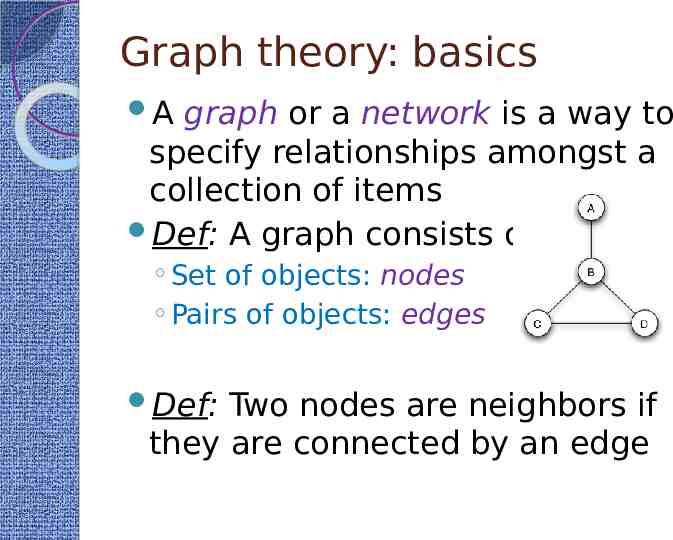
Graph theory: basics A graph or a network is a way to specify relationships amongst a collection of items Def: A graph consists of Set of objects: nodes Pairs of objects: edges Def: Two nodes are neighbors if they are connected by an edge

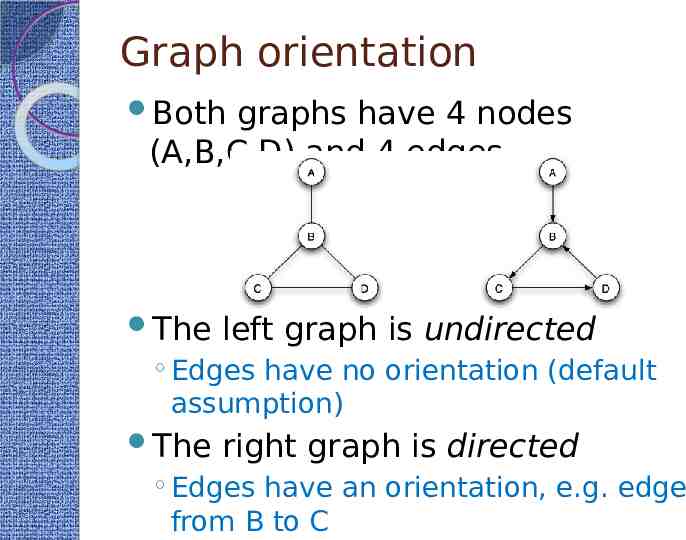
Graph orientation Both graphs have 4 nodes (A,B,C,D) and 4 edges The left graph is undirected Edges have no orientation (default assumption) The right graph is directed Edges have an orientation, e.g. edge from B to C

Weighted graphs Edges may also carry additional information Signs (are we friends or enemies?) Tie strength (how good are we as friends?) Distance (how long is this road?) Delay (how long does the transmission take?) Def: In a weighted graph, every edge has an associated number called a weight. Def: In a signed graph, every edge has a or a – sign associated with it.

Transportation networks Graph terminology often derived from transportation metaphors E.g. “shortest path“, “flow“, “diameter“

An electrical network The physics of Kirchoff‘s laws is applied at every network node and closed paths to design circuits

Graph concepts “Graph theory is a terminological jungle in which every newcomer may plant a tree“ (Social scientist John Barnes) We will focus on the most central concepts Paths between nodes Cycles Connectivity Components (and giant component) Distance (and search) Measures on nodes and networks as a whole

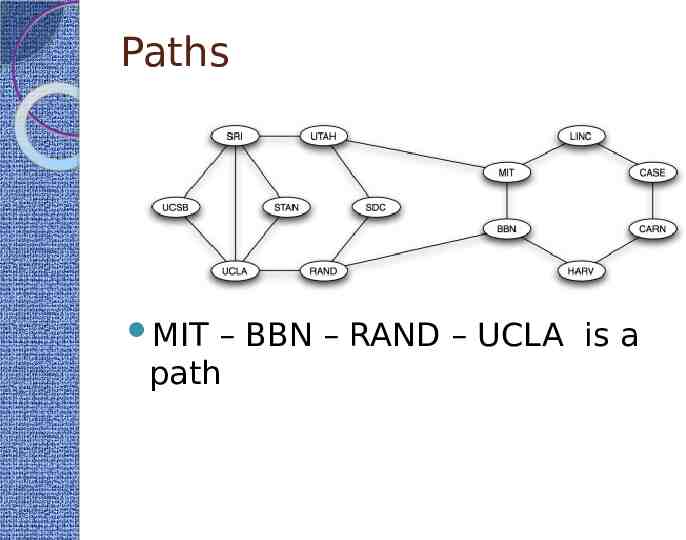
Paths Things often travel along the edges of a graph Travel Information Physical quantities Def: A path is sequence of nodes with the property that each consecutive pair in the sequence is connected by an edge Can also be defined as a sequence of edges

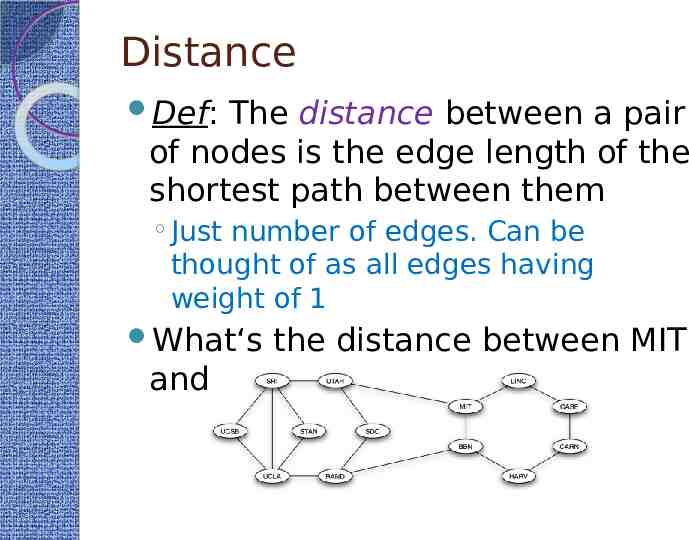
Paths MIT – BBN – RAND – UCLA is a path

Paths You could also traverse the same node multiple times SRI – STAN – UCLA – SRI – UTAH – MIT This is called a non-simple path Paths in which nodes are not repeated are called simple paths

Cycles These are ring structures that begin and end in the same node LINC – CASE – CARN – HARV – BBN – MIT – LINC is a cycle Def: A cycle is a closed path with at least three edges In the 1970 ARPANET, every edge is on a cycle By design. Why?

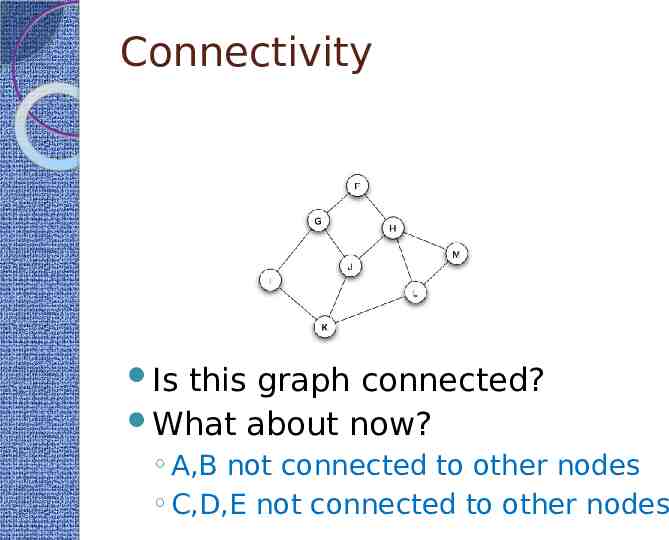
Connectivity Can every node in a graph be reached from any other node through a path? If so, the graph is connected In many cases, graphs may be disconnected Social networks Collaboration networks etc.

Connectivity Is this graph connected? What about now? A,B not connected to other nodes C,D,E not connected to other nodes

Components If a graph is not connected, it tends to break into pieces that themselves are connected Def: The connected components of an undirected graph are groups of nodes with the property that the groups are connected, and no two groups overlap More precisely: A connected component is a subset of nodes such that (1) every node has a path to every other node in the subset, and (2) the subset is not a part of a larger set with the property that every node can reach another

Components: Analysis A first global way to look at graph structure For instance, we can understand what is holding a component together Real-world biology collaboration graph

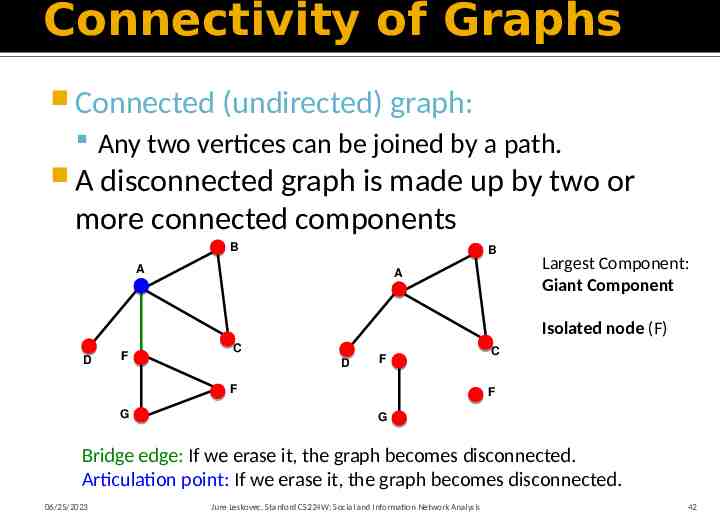
Connectivity of Graphs Connected (undirected) graph: Any two vertices can be joined by a path. A disconnected graph is made up by two or more connected components B B A A Largest Component: Giant Component Isolated node (F) D F C D F F G C F G Bridge edge: If we erase it, the graph becomes disconnected. Articulation point: If we erase it, the graph becomes disconnected. 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 42

Components: Analysis Analyzing graphs in terms of densely connected regions and the boundaries of regions For instance, only include edges with weights above a threshold, then gradually increase the threshold The graph will fragment into more and more components We will later see how this becomes an important type of analysis

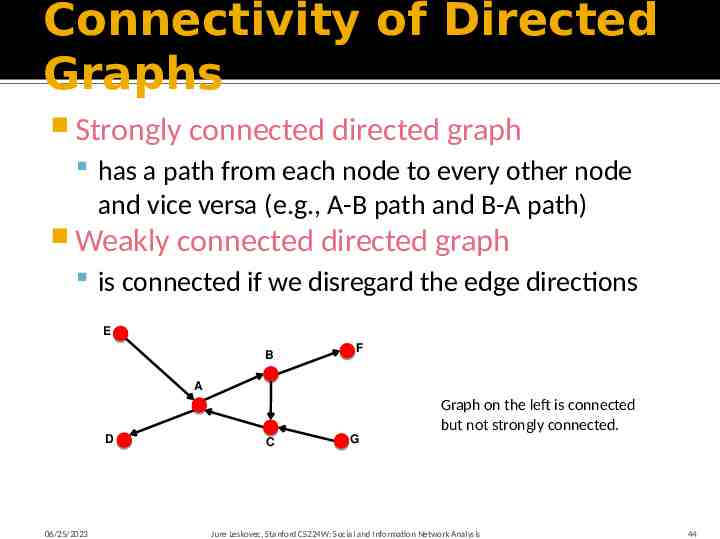
Connectivity of Directed Graphs Strongly connected directed graph has a path from each node to every other node and vice versa (e.g., A-B path and B-A path) Weakly connected directed graph is connected if we disregard the edge directions E B F A Graph on the left is connected but not strongly connected. D 06/25/2023 C G Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 44

Giant components Many graphs are not connected, but may include a very large connected components E.g. the financial graph earlier, the hyperlink graph of the web, . Large complex networks often contain a giant component A component that holds a large percentage of all nodes Rare that two or more of these will exist in a graph. Why?

Distance Def: The distance between a pair of nodes is the edge length of the shortest path between them Just number of edges. Can be thought of as all edges having weight of 1 What‘s the distance between MIT and SDC?

Distance Q: Given a graph, how do we find distances between a given node and all other nodes systematically? Need to define an algorithm! How would you approach this problem?

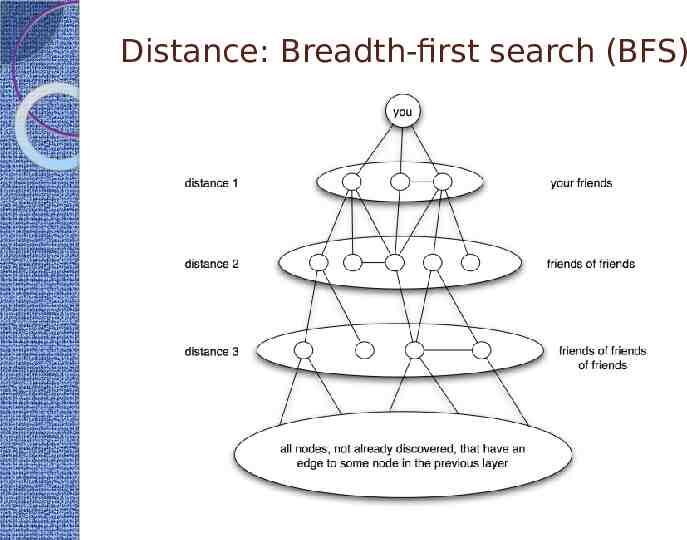
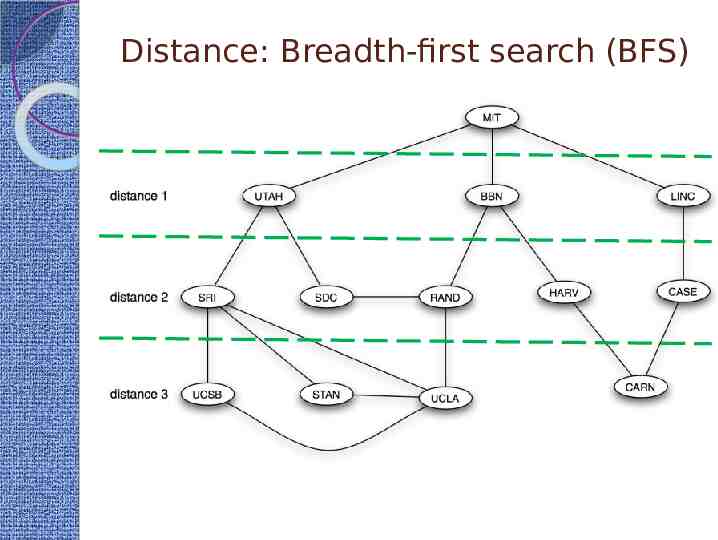
Distance: Breadth-first search (BFS) From the given node (root) Find all nodes that are directly connected These are labeled as “distance 1“(1-hop, egonet) Find all nodes that are directly connected to nodes at distance 1 If these nodes are not at distance 1, we label them as “distance 2“ (2-hop) . Find all nodes that are directly connected to nodes at distance j (j-hop) If these nodes are not already of distance at most j 1, we label them as „distance j 1“

Distance: Breadth-first search (BFS)

Distance: Breadth-first search (BFS)

Six degrees of geekiness Co-authorship Erdös graph centered on Paul

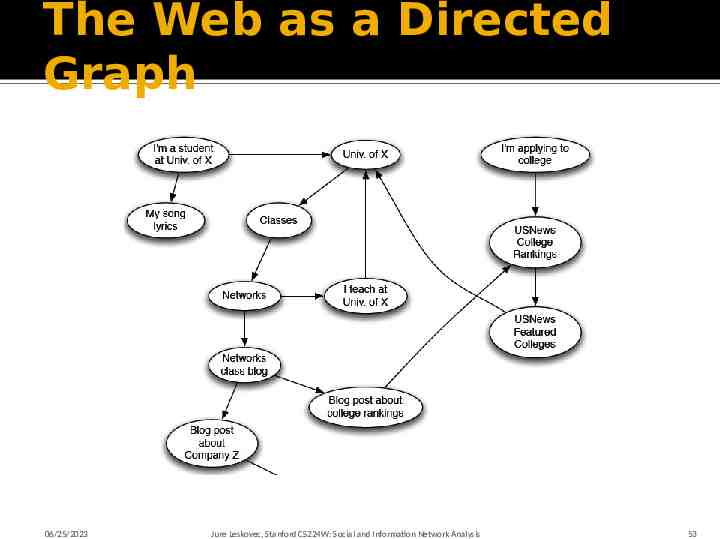
Web as a Graph Q: What does Web “look like” at a global level? Web as a graph: Nodes pages Edges hyperlinks What is a node? Problems: Dynamic pages created on the fly “dark matter” – inaccessible database generated pages In early days of the Web links were navigational Today many links are transactional 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 52

The Web as a Directed Graph 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 53

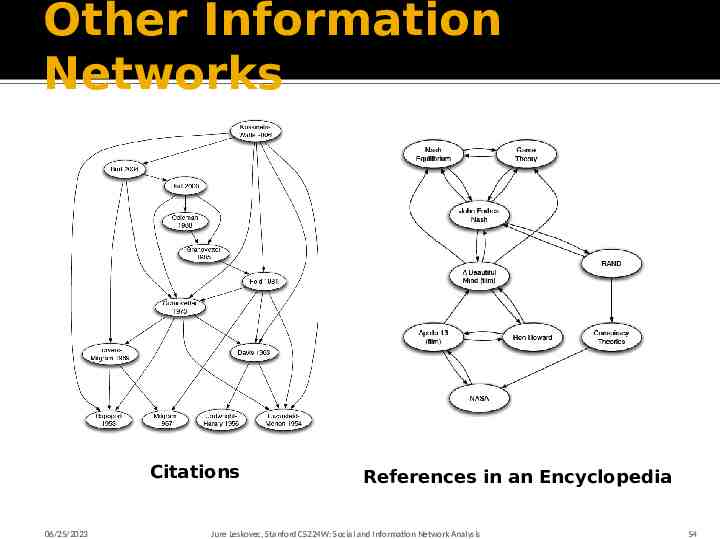
Other Information Networks Citations 06/25/2023 References in an Encyclopedia Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 54

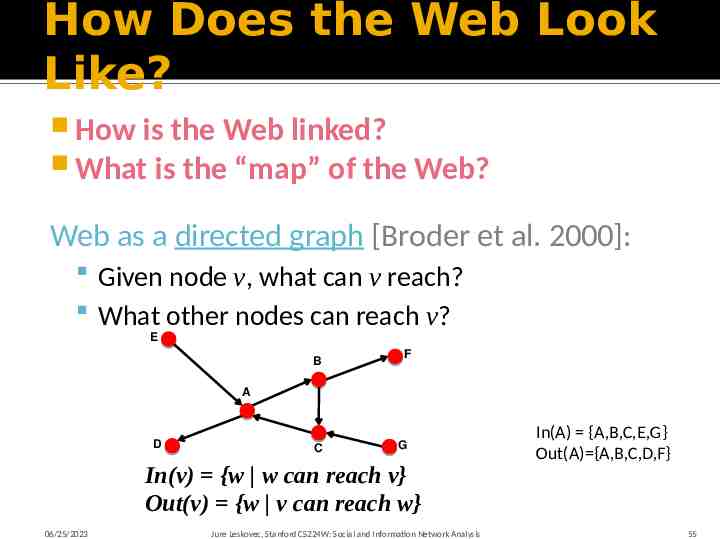
How Does the Web Look Like? How is the Web linked? What is the “map” of the Web? Web as a directed graph [Broder et al. 2000]: Given node v, what can v reach? What other nodes can reach v? E B F A D C G In(v) {w w can reach v} Out(v) {w v can reach w} 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis In(A) {A,B,C,E,G} Out(A) {A,B,C,D,F} 55

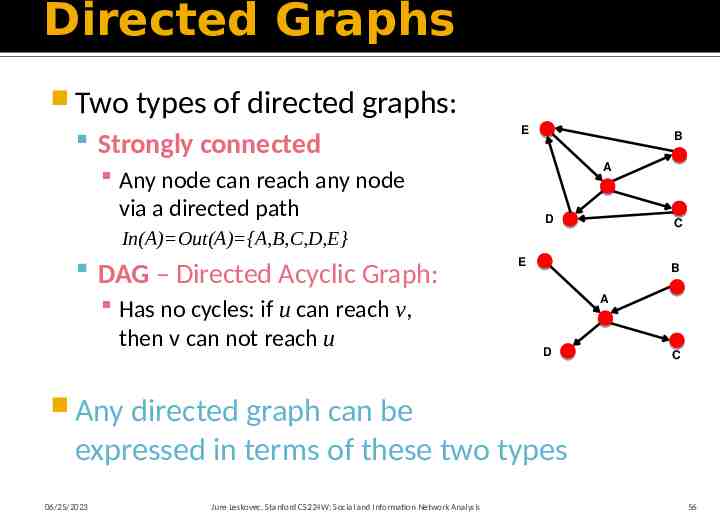
Directed Graphs Two types of directed graphs: Strongly connected E B A Any node can reach any node via a directed path D C In(A) Out(A) {A,B,C,D,E} DAG – Directed Acyclic Graph: Has no cycles: if u can reach v, then v can not reach u E B A D C Any directed graph can be expressed in terms of these two types 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 56

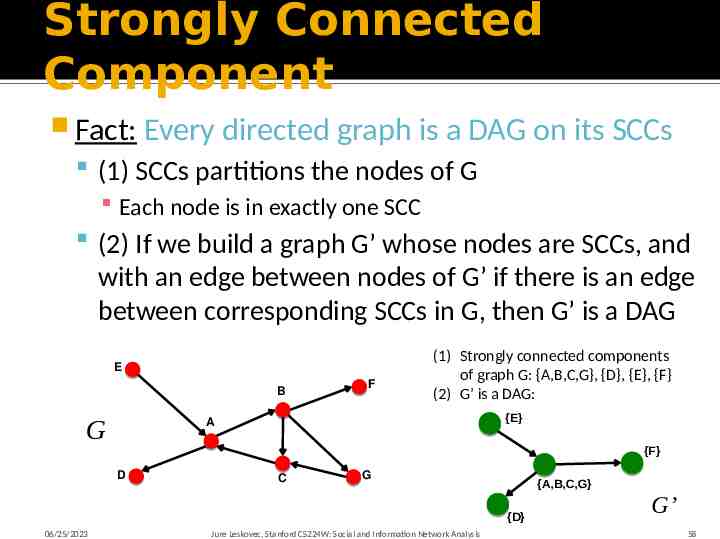
Strongly Connected Component Strongly connected component (SCC) is a set of nodes S so that: Every pair of nodes in S can reach each other There is no larger set containing S with this property E B F A D 06/25/2023 C G Strongly connected components of the graph: {A,B,C,G}, {D}, {E}, {F} Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 57

Strongly Connected Component Fact: Every directed graph is a DAG on its SCCs (1) SCCs partitions the nodes of G Each node is in exactly one SCC (2) If we build a graph G’ whose nodes are SCCs, and with an edge between nodes of G’ if there is an edge between corresponding SCCs in G, then G’ is a DAG E B G F (1) Strongly connected components of graph G: {A,B,C,G}, {D}, {E}, {F} (2) G’ is a DAG: {E} A {F} D C G {A,B,C,G} {D} 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis G’ 58

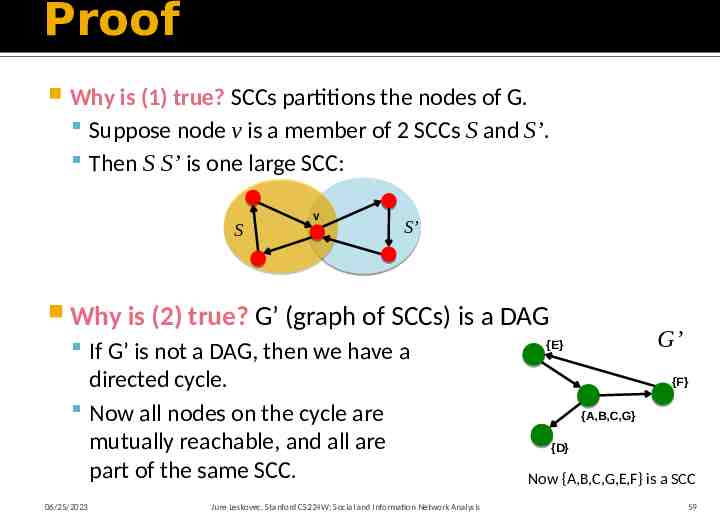
Proof Why is (1) true? SCCs partitions the nodes of G. Suppose node v is a member of 2 SCCs S and S’. Then S S’ is one large SCC: S v S’ Why is (2) true? G’ (graph of SCCs) is a DAG If G’ is not a DAG, then we have a directed cycle. Now all nodes on the cycle are mutually reachable, and all are part of the same SCC. 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis G’ {E} {F} {A,B,C,G} {D} Now {A,B,C,G,E,F} is a SCC 59

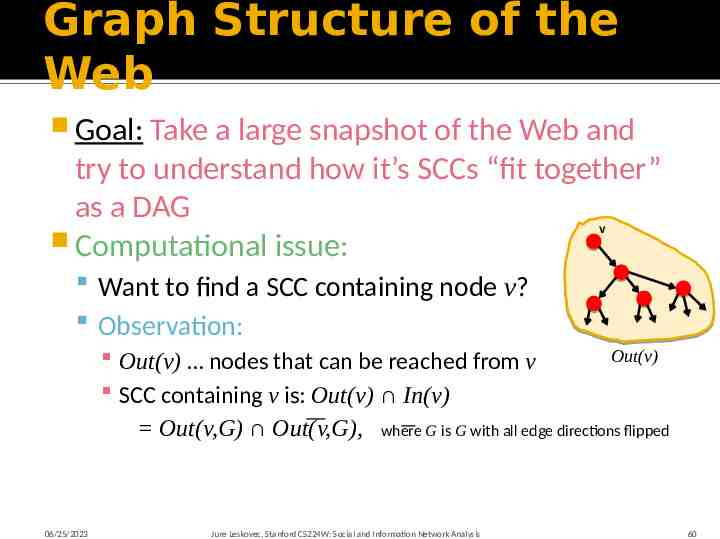
Graph Structure of the Web Goal: Take a large snapshot of the Web and try to understand how it’s SCCs “fit together” as a DAG Computational issue: v Want to find a SCC containing node v? Observation: Out(v) nodes that can be reached from v SCC containing v is: Out(v) In(v) Out(v,G) Out(v,G), 06/25/2023 Out(v) where G is G with all edge directions flipped Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 60

Graph Structure of the Web There is a giant SCC There won’t be 2 giant SCCs: It just takes 1 page from one SCC to link to the other SCC If the components have millions of pages the likelihood of this not happening is very small Giant SCC1 06/25/2023 Giant SCC2 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 61

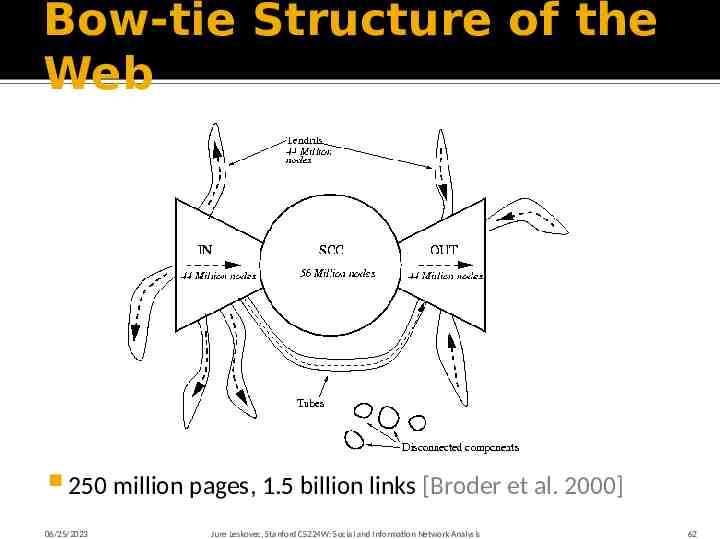
Bow-tie Structure of the Web 250 million pages, 1.5 billion links 06/25/2023 [Broder et al. 2000] Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 62

More on the web graph What we mentioned: Some conceptual organization of the Web (i.e., the bowtie) What we haven’t learned yet: We treats all pages as equal Google’s homepage my homepage What are the most important pages? How many pages have k in-links as a function of k? The degree distribution: 1 / k2 Link analysis ranking -- as done by search engines (PageRank) What is the internal structure inside the giant SCC? Clusters, implicit communities? How far apart are nodes in the giant SCC: Distance # of edges in shortest path Avg 16 [Broder et al.] 06/25/2023 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis 63

Network data sets Chapter 2 includes an overview of some massive data sets and networks Collaboration graphs Wikipedia, World of Warcraft, Citation graphs Who-talks-to-whom graphs Microsoft IM, Cell phone graphs Information linkage Hyperlinks Technological networks Power grids, communication links, Internet Natural and biological networks Food webs, neural interconnections, cell metabolism

Network data sets Leskovec‘s SNAP at Stanford has a repository of large-scale networks http://snap.stanford.edu/data

Recap A graph consists of nodes and edges Graphs can be directed or undirected, weighted, signed or unweighted Paths between nodes (simple vs. non-simple) Cycles Connectivity Components (and the giant component) Distance (and BFS) Strongly connected components, DAGs Bow-tie structure of the web Six degrees of separation can be checked with BFS