CSE 332: Data Structures and Parallelism Spring 2022 Richard Anderson

CSE 332: Data Structures and Parallelism Spring 2022 Richard Anderson Lecture 20: Analysis of Fork-Join Programs 11/16/2022 CSE 332 1

Announcements Read parallel computing notes by Dan Grossman 2.1-4.3 Bring laptop to section this week with IntelliJ set up – Work on fork-join parallelism for most of section 11/16/2022 CSE 332 2

Midterm Problems 11/16/2022 CSE 332 3

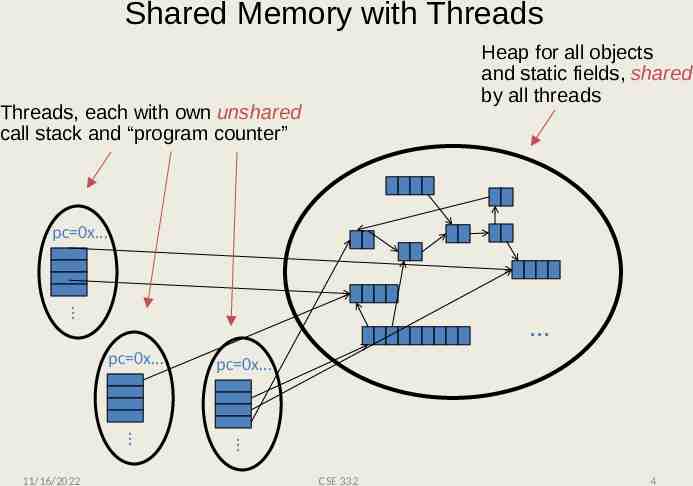
Shared Memory with Threads Heap for all objects and static fields, shared by all threads Threads, each with own unshared call stack and “program counter” pc 0x pc 0x pc 0x 11/16/2022 CSE 332 4

Threads and Processors Simple model – Threads are either running or idle – Processors select idle threads and execute them for “a while” Scheduling of threads is outside of the scope of this course – Many different approaches – Programmer has limited control on scheduling T1 T2 P1 11/16/2022 T3 T4 P2 T5 T6 P3 CSE 332 5

Fork-Join Parallelism 1. Define thread – Java: define subclass of java.lang.Thread, – Override run implement operation of the thread 2. Fork: instantiate a thread and start executing – Java: create thread object, call start() 3. Join: wait for thread to terminate – Java: call join() method, which returns when thread finishes Above uses basic thread library build into Java Later we’ll introduce a better ForkJoin Java library designed for parallel programming 11/16/2022 CSE 332 6

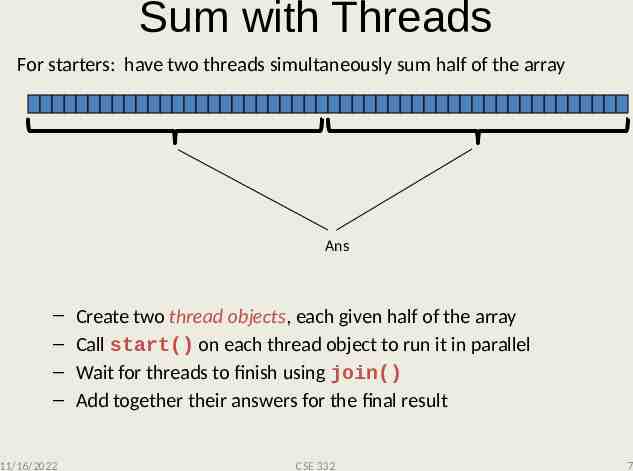
Sum with Threads For starters: have two threads simultaneously sum half of the array Ans – – – – 11/16/2022 Create two thread objects, each given half of the array Call start() on each thread object to run it in parallel Wait for threads to finish using join() Add together their answers for the final result CSE 332 7

Part 1: define thread class class SumThread extends java.lang.Thread { int lo; // fields, passed to constructor int hi; // so threads know what to do. int[] arr; int ans 0; // result SumThread(int[] a, int l, int h) { lo l; hi h; arr a; } } public void run() { for(int i lo; i hi; i ) ans arr[i]; } Because we must override a no-arguments/no-result run, we use fields to communicate across threads 11/16/2022 CSE 332 8

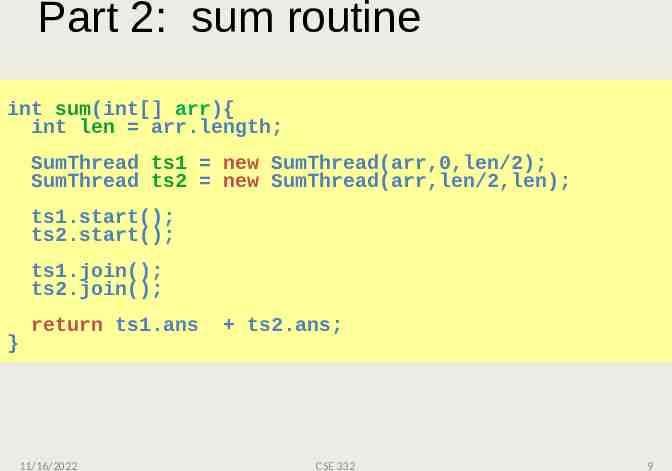
Part 2: sum routine int sum(int[] arr){ int len arr.length; SumThread ts1 new SumThread(arr,0,len/2); SumThread ts2 new SumThread(arr,len/2,len); ts1.start(); ts2.start(); ts1.join(); ts2.join(); } return ts1.ans 11/16/2022 ts2.ans; CSE 332 9

Parameterizing by number of threads int sum(int[] arr, int numTs){ int ans 0; SumThread[] ts new SumThread[numTs]; for(int i 0; i numTs; i ){ ts[i] new SumThread(arr,(i*arr.length)/numTs, ((i 1)*arr.length)/numTs); ts[i].start(); } for(int i 0; i numTs; i ) { ts[i].join(); ans ts[i].ans; } return ans; } 11/16/2022 CSE 332 10

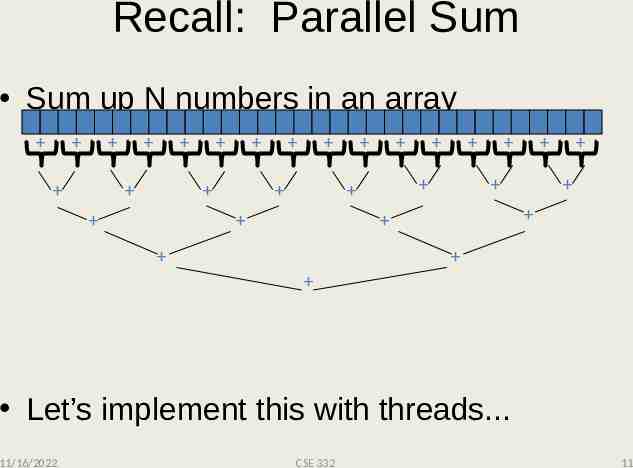
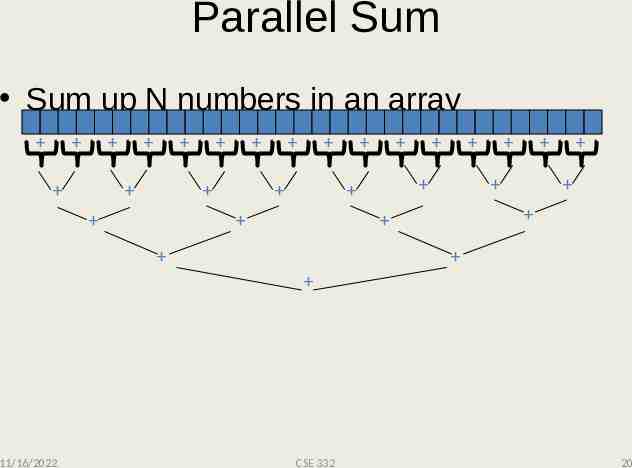
Recall: Parallel Sum Sum up N numbers in an array Let’s implement this with threads. 11/16/2022 CSE 332 11

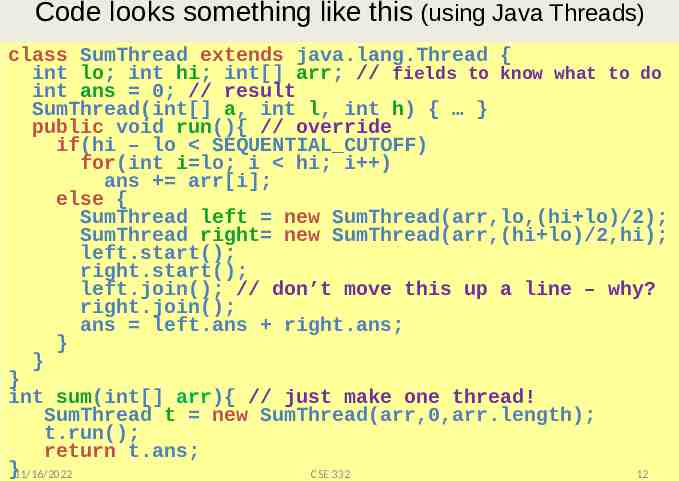
Code looks something like this (using Java Threads) class SumThread extends java.lang.Thread { int lo; int hi; int[] arr; // fields to know what to do int ans 0; // result The key is to do thea, result-combining in { parallel SumThread(int[] int l, int h) } as well public void recursive run(){ divide-and-conquer // override – And using makes this natural if(hi – lo SEQUENTIAL CUTOFF) – Easier to write and more asymptotically! for(int i lo; i efficient hi; i ) ans arr[i]; else { SumThread left new SumThread(arr,lo,(hi lo)/2); SumThread right new SumThread(arr,(hi lo)/2,hi); left.start(); right.start(); left.join(); // don’t move this up a line – why? right.join(); ans left.ans right.ans; } } } int sum(int[] arr){ // just make one thread! SumThread t new SumThread(arr,0,arr.length); t.run(); return t.ans; }11/16/2022 CSE 332 12

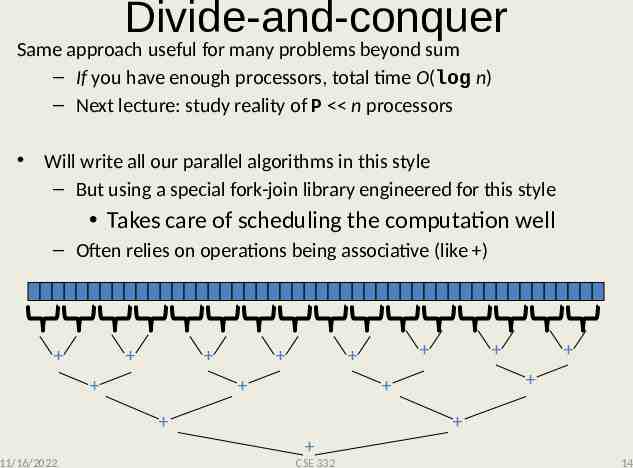
Recursive problem decomposition Thread: sum range [0,10) Thread: sum range [0,5) Thread: sum range [0,2) Thread: sum range [0,1) (return arr[0]) Thread: sum range [1,2) (return arr[1]) add results from two helper threads Thread: sum range [2,5) Thread: sum range [2,3) (return arr[2]) Thread: sum range [3,5) Thread: sum range [3,4) (return arr[3]) Thread: sum range [4,5) (return arr[4]) add results from two helper threads add results from two helper threads add results from two helper threads Thread: sum range [5,10) Thread: sum range [5,7) Thread: sum range [5,6) (return arr[5]) Thread: sum range [6,7) (return arr[6]) add results from two helper threads Thread: sum range [7,10) Thread: sum range [7,8) (return arr[7]) Thread: sum range [8,10) Thread: sum range [8,9) (return arr[8]) Thread: sum range [9,10) (return arr[9]) add results from two helper threads add results from two helper threads add results from two helper threads 11/16/2022 CSE 332 13

Divide-and-conquer Same approach useful for many problems beyond sum – If you have enough processors, total time O(log n) – Next lecture: study reality of P n processors Will write all our parallel algorithms in this style – But using a special fork-join library engineered for this style Takes care of scheduling the computation well – Often relies on operations being associative (like ) 11/16/2022 CSE 332 14

Thread Overhead Creating and managing threads incurs cost Two optimizations: 1. Use a sequential cutoff, typically around 500-1000 Eliminates lots of tiny threads 2. Do not create two recursive threads; create one thread and do the other piece of work “yourself” 11/16/2022 Cuts the number of threads created by another 2x CSE 332 15

Half the threads! order of last 4 lines Is critical – why? // wasteful: don’t SumThread left SumThread right // better: do!! SumThread left SumThread right left.start(); right.start(); left.start(); right.run(); left.join(); right.join(); ans left.ans right.ans; 11/16/2022 Note: run is a normal function call! execution won’t continue until we are done with run left.join(); // no right.join needed ans left.ans right.ans; CSE 332 16

Better Java Thread Library Even with all this care, Java’s threads are too “heavyweight” – Constant factors, especially space overhead – Creating 20,000 Java threads just a bad idea The ForkJoin Framework is designed to meet the needs of divideand-conquer fork-join parallelism – In the Java 8 standard libraries – Section will focus on pragmatics/logistics – Similar libraries available for other languages C/C : Cilk (inventors), Intel’s Thread Building Blocks C#: Task Parallel Library 11/16/2022 CSE 332 17

Different terms, same basic idea To use the ForkJoin Framework: A little standard set-up code (e.g., create a ForkJoinPool) Don’t subclass Thread Do subclass RecursiveTask V Don’t override run Do override compute Do not use an ans field Do return a V from compute Don’t call start Do call fork Don’t just call join Do call join (which returns answer) Don’t call run to hand-optimize Do call compute to hand-optimize Don’t have a topmost call to run Do create a pool and call invoke See the web page for (linked from Handouts page on course website): “A Beginner’s Introduction to the ForkJoin Framework” 11/16/2022 CSE 332 18

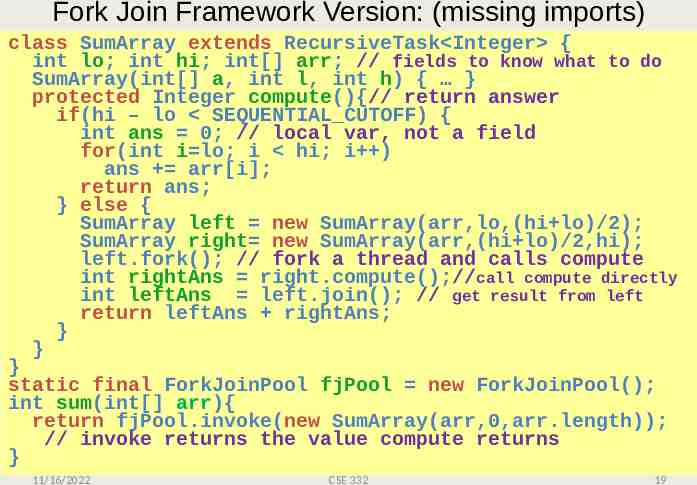
Fork Join Framework Version: (missing imports) class SumArray extends RecursiveTask Integer { int lo; int hi; int[] arr; // fields to know what to do SumArray(int[] a, int l, int h) { } protected Integer compute(){// return answer if(hi – lo SEQUENTIAL CUTOFF) { int ans 0; // local var, not a field for(int i lo; i hi; i ) ans arr[i]; return ans; } else { SumArray left new SumArray(arr,lo,(hi lo)/2); SumArray right new SumArray(arr,(hi lo)/2,hi); left.fork(); // fork a thread and calls compute int rightAns right.compute();//call compute directly int leftAns left.join(); // get result from left return leftAns rightAns; } } } static final ForkJoinPool fjPool new ForkJoinPool(); int sum(int[] arr){ return fjPool.invoke(new SumArray(arr,0,arr.length)); // invoke returns the value compute returns } 11/16/2022 CSE 332 19

Parallel Sum Sum up N numbers in an array 11/16/2022 CSE 332 20

Parallel Max? 11/16/2022 CSE 332 21

Reductions Same trick works for many tasks, e.g., – – – – is there an element satisfying some property (e.g., prime) left-most element satisfying some property (e.g., first prime) counts: number of strings that start with a vowel are these elements in sorted order? Called a reduction, or reduce operation – reduce a collection of data items to a single item result can be more than a single value, e.g., produce histogram from a set of test scores Very common parallel programming pattern 11/16/2022 CSE 332 22

Parallel Vector Scaling Multiply every element in the array by 2 11/16/2022 CSE 332 23

Maps A map operates on each element of a collection of data to produce a new collection of the same size – each element is processed independently of the others, e.g. vector scaling vector addition test property of each element (is it prime) uppercase to lowercase . Another common parallel programming pattern 11/16/2022 CSE 332 24

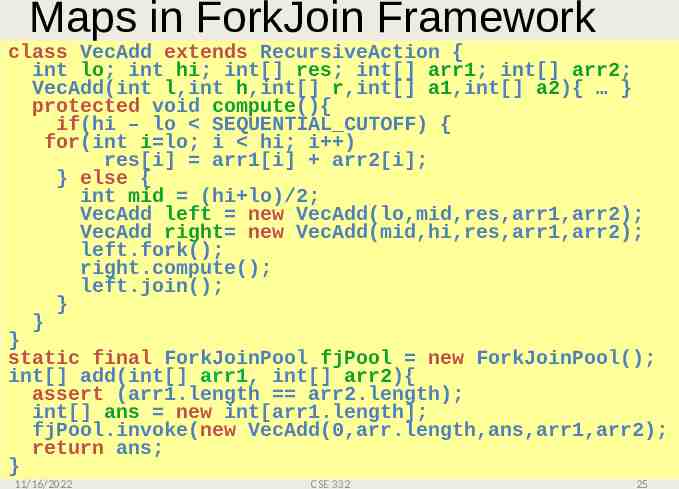
Maps in ForkJoin Framework class VecAdd extends RecursiveAction { int lo; int hi; int[] res; int[] arr1; int[] arr2; VecAdd(int r,int[] a1,int[] a2){with } Even thoughl,int there h,int[] is no result-combining, it still helps protected void compute(){ load balancing create many small tasks if(hi – lo toSEQUENTIAL CUTOFF) { for(int i lo; i hi;but i ) – Maybe not for vector-add for more compute-intensive maps res[i] arr1[i] arr2[i]; – The forking } else { is O(log n) whereas theoretically other approaches to vector-add int mid is O(1) (hi lo)/2; VecAdd left new VecAdd(lo,mid,res,arr1,arr2); VecAdd right new VecAdd(mid,hi,res,arr1,arr2); left.fork(); right.compute(); left.join(); } } } static final ForkJoinPool fjPool new ForkJoinPool(); int[] add(int[] arr1, int[] arr2){ assert (arr1.length arr2.length); int[] ans new int[arr1.length]; fjPool.invoke(new VecAdd(0,arr.length,ans,arr1,arr2); return ans; } 11/16/2022 CSE 332 25

Maps and Reductions Maps and reductions: the “workhorses” of parallel programming – By far the most important and common patterns – Learn to recognize when an algorithm can be written in terms of maps and reductions – makes parallel programming easy (plug and play) 11/16/2022 CSE 332 26

Distributed Map Reduce You may have heard of Google’s map/reduce – or open-source version called Hadoop – powers much of Google’s infrastructure Idea: maps/reductions using many machines – same principles, applied to distributed computing – system takes care of distributing data, fault-tolerance – you just write code to handle one element, reduce a collection Co-developed by Jeff Dean (UW alum!) 11/16/2022 CSE 332 27

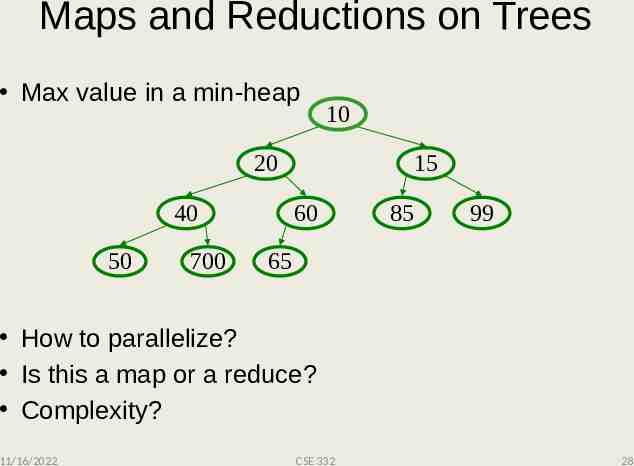
Maps and Reductions on Trees Max value in a min-heap 10 20 40 50 700 15 60 85 99 65 How to parallelize? Is this a map or a reduce? Complexity? 11/16/2022 CSE 332 28

Analyzing Parallel Programs Let TP be the running time on P processors Two key measures of run-time: Work: How long it would take 1 processor T1 Span: How long it would take infinity processors T – – – – 11/16/2022 The hypothetical ideal for parallelization This is the longest “dependence chain” in the computation Example: O(log n) for summing an array Also called “critical path length” or “computational depth” CSE 332 29

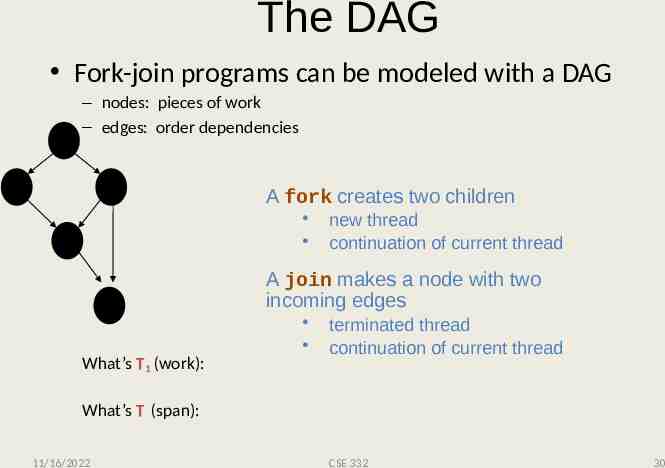
The DAG Fork-join programs can be modeled with a DAG – nodes: pieces of work – edges: order dependencies A fork creates two children new thread continuation of current thread A join makes a node with two incoming edges What’s T1 (work): terminated thread continuation of current thread What’s T (span): 11/16/2022 CSE 332 30

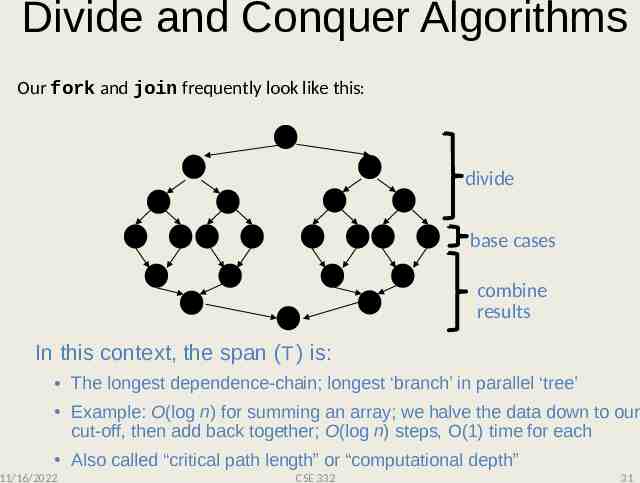
Divide and Conquer Algorithms Our fork and join frequently look like this: divide base cases combine results In this context, the span (T ) is: The longest dependence-chain; longest ‘branch’ in parallel ‘tree’ Example: O(log n) for summing an array; we halve the data down to our cut-off, then add back together; O(log n) steps, O(1) time for each Also called “critical path length” or “computational depth” 11/16/2022 CSE 332 31

Parallel Speed-up Speed-up on P processors: T1 / TP If speed-up is P, we call it perfect linear speed-up – e.g., doubling P halves running time – hard to achieve in practice Parallelism is the maximum possible speed-up: T1 / T – if you had infinite processors 11/16/2022 CSE 332 32

Estimating Tp How to estimate TP (e.g., P 4)? Lower bounds on TP (ignoring memory, caching.) 1. T 2. T1 / P – which one is the tighter (higher) lower bound? The ForkJoin Java Framework achieves the following expected time asymptotic bound: TP ϵ O(T T1 / P) – this bound is optimal 11/16/2022 CSE 332 33

Amdahl’s Law Most programs have 1. parts that parallelize well 2. parts that don’t parallelize at all The latter become bottlenecks 11/16/2022 CSE 332 34

Amdahl’s Law Let T1 1 unit of time Let S proportion that can’t be parallelized 1 T1 S (1 – S) Suppose we get perfect linear speedup on the parallel portion: TP So the overall speed-up on P processors is (Amdahl’s Law): T1 / T P T1 / T If 1/3 of your program is parallelizable, max speedup is: 11/16/2022 CSE 332 35

Pretty Bad News Suppose 25% of your program is sequential. – Then a billion processors won’t give you more than a 4x speedup! What portion of your program must be parallelizable to get 10x speedup on a 1000 core GPU? – 10 1 / (S (1-S)/1000) Motivates minimizing sequential portions of your programs 11/16/2022 CSE 332 36

Take Aways Parallel algorithms can be a big win Many fit standard patterns that are easy to implement Can’t just rely on more processors to make things faster (Amdahl’s Law) 11/16/2022 CSE 332 37