CSCI 3333 Data Structures Dictionaries and Hashing

CSCI 3333 Data Structures Dictionaries and Hashing

Acknowledgement Dr. Yue Ms. Krishani Abeysekera Mr. Charles Moen Dr. Wei Ding Dr. Michael Goodrich

Fast Searching Balanced BST, Binary Search, etc: O(lg n) average time in searching. Can it be faster? Can we have O(1) searching time?

Dictionary A dictionary, in computer science, implies a container that stores keyelement pairs called items, and allows for quick retrieval. Items must be stored in a way that allows them to be located with the key Not necessary to store the items in order Unordered dictionary Ordered dictionary

Dictionary ADT Operations in a Dictionary ADT: int size() bool isEmpty() iter elements() iter keys() pos find( key ) iter findAll( key ) void insertItem( key, elem ) void removeElement( key ) void removeAllElements( key )

Hashing A procedure to convert large data into a small indexed data. A hash table, or a hash map, is a data structure that associates keys with values Compiler Example: Parsing: programs - tokens Token handling Constructing a symbol table. Checking whether a token is a reserve word. Other steps Other steps

Minimal Perfect Hashing Function A procedure to map distinct data with distinct index, with no collision. For a token t, the hash address is computed by Addr(t) t.length val(t[0]) val(t[t.length-1]) – 2. The val array where the index is ‘a’ to ‘z’ is given by: A 11, B 15, C 1, D 0, E 0, F 15, G 3, H 15,1 13, J 0, K 0, L 15, M 15, N 13, O 0, P 15, Q 0, R 14, S 6, T 6, U 14, V 10, W 6, X 0, Y 13, Z 0. E.g. val[’A’] 11. val[‘Y’] 13.

Reserved words Pascal reserved words can thus be stored using these addresses: reserved[0] “DO” reserved[1] “END” reserved[35] “PROGRAM”

Lessons Learnt In hashing, the address is computed. In binary searching and BST, address is navigated to through comparisons. It is desirable that each record is hashed in different address (perfect hashing). It is desirable if all addresses are filled (minimal hashing). In compilers (and many other applications), minimal perfect hashing is highly desirable.

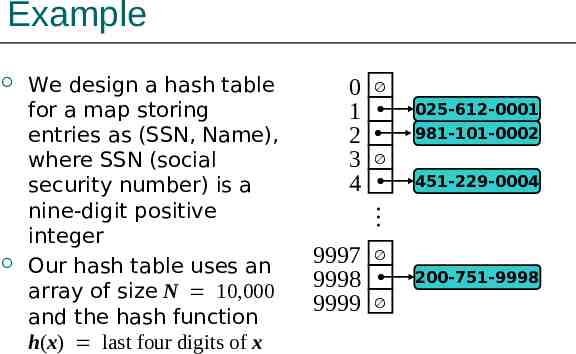
Example 0 1 2 3 4 025-612-0001 981-101-0002 451-229-0004 We design a hash table for a map storing entries as (SSN, Name), where SSN (social security number) is a nine-digit positive integer Our hash table uses an array of size N 10,000 and the hash function h(x) last four digits of x 9997 9998 9999 200-751-9998

Question Is it better or worse to use the first four digits instead of the last four digits of the social security number?

Hashing Issues Two main problems in hashing: Selecting good hashing functions. Handling collision (when more than one records are hashed into the same address).

Example Consider a hash function of people names: hash(name) val(first char of last name) * 100 val(middle initial) where val(char) ascii(char) – ascii(‘A’) 1. Is this good?

Bucket Arrays A Bucket array for a hash table, is an array A of size N, where each cell of A is thought of as a ‘bucket’, and N defines the capacity of the array. Example Small company with less than 100 employees Each employee has an ID number in the range 0–99 Store employee records in an array, so that the employee ID number matches the array index A 0 1 2 3 4 EMPTY 01 Turing, A. 02 Babbage, C. EMPTY 04 Gates, W.

Bucket Arrays If the keys are unique, then searches, insertions and removals in the bucket array take worst-case time of O(1). However, bucket arrays have 2 drawbacks. It requires a capacity of N (which is the maximum number of elements possible The key has to be a integer in the range [0, N1]

Hash Functions and Hash Values A hash function is a way of creating a unique data. A function modifies or chops or mixes the data to create a fingerprint data called a hash value. To do this, the index of the hash table's array is generally calculated in two steps: A generic hash value could be calculated in many ways to map the key to an integer, called hash code. This value is reduced to a valid array index, often called compression map.

Hash code examples Integer Cast int hashCode( char key ){ return (int(key) ); } Summing int hashCode( long key ){ typedef unsigned long ulong; return ( int( ulong(key) 32 ) int( key );} Polynomial s 115 * 103 115000 t 116 * 102 11600 o 111 * 101 1110 p 112 * 100 112 Hashcode 127822

Hash Function Properties A good hash function should: be easy and quick to compute. achieve an even distribution of the key values that actually occur across the index range supported by the table - avoid collision. Desirable properties: Perfect: no collision. No two keys are mapped to the same address. Minimal: the entire address range is used up entirely. Ordered: to facilitate traversal.