CS 431/636 Advanced Rendering Techniques Dr. David Breen University
57 Slides2.59 MB
CS 431/636 Advanced Rendering Techniques Dr. David Breen University Crossings 149 Tuesday 6PM 8:50PM Presentation 1 3/31/09
Class Topics and Objectives Photo-realistic image generation Ray Tracing! Learn and implement the algorithms needed to create ray traced images Serious numerical computing and programming class Assumes you know CG I material
Class Structure Weekly lectures & reading assignments 6 regular programming assignments 1 extra credit assignment Post images on the web E-mail the URL to [email protected] Upload code to WebCT Grad students give presentations No final exam
Grading Graduate Section Undergraduate Section Programming Assignments - 90% In-class Presentation - 10% Programming Assignments - 95% Class Participation (Attend class on Week 5) - 5% Late policy 1 point/day Maximum 5 points off
Go To Web Sites Class web site Previous pictures web site
Slide Credits Kevin Suffern - University of Technology, Sydney, Australia G. Drew Kessler & Larry Hodges - Georgia Institute of Technology Fredo Durand & Barb Cutler - MIT Computer Graphics I
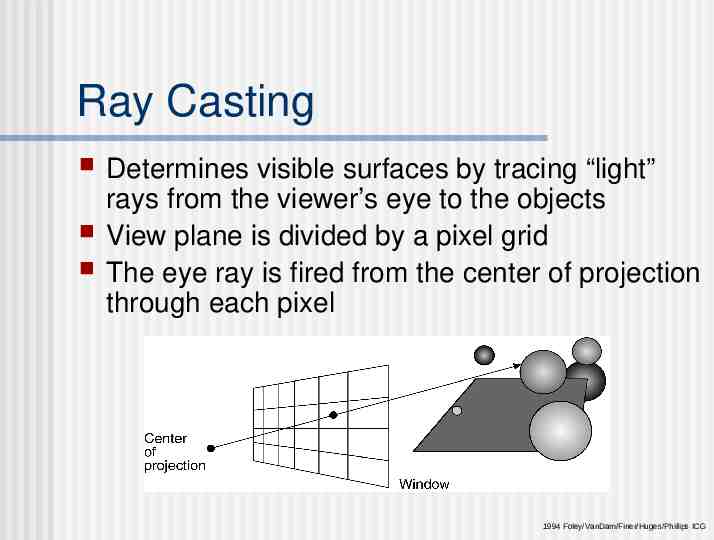
Ray Casting Determines visible surfaces by tracing “light” rays from the viewer’s eye to the objects View plane is divided by a pixel grid The eye ray is fired from the center of projection through each pixel 1994 Foley/VanDam/Finer/Huges/Phillips ICG
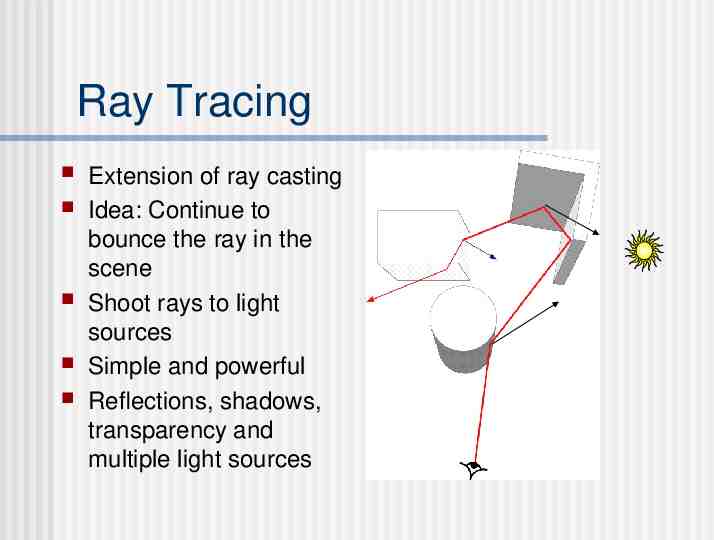
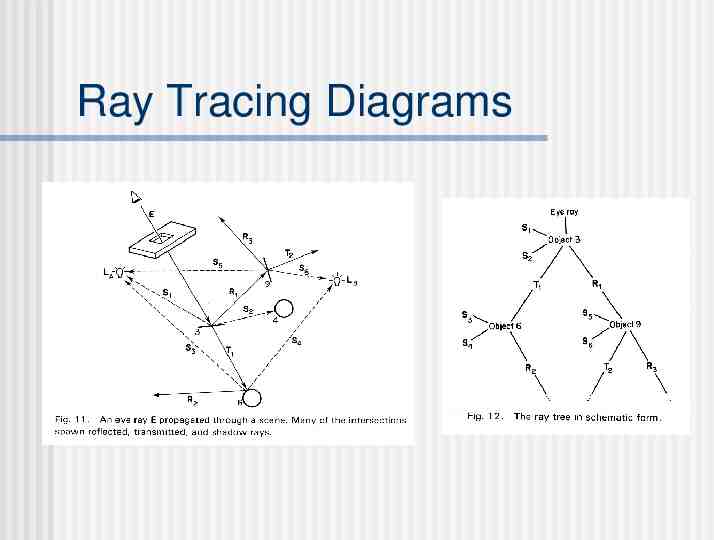
Ray Tracing Extension of ray casting Idea: Continue to bounce the ray in the scene Shoot rays to light sources Simple and powerful Reflections, shadows, transparency and multiple light sources
Ray Tracing Diagrams
First Ray-Traced Image Whitted 1980
Issues Ray-object intersections Complex, hierarchical models (CSG?) Transformations Camera models Recursive algorithms Surface physics (shading models) Color representations Light representations Sampling, anti-aliasing and filtering Geometric optics Acceleration techniques Texture mapping
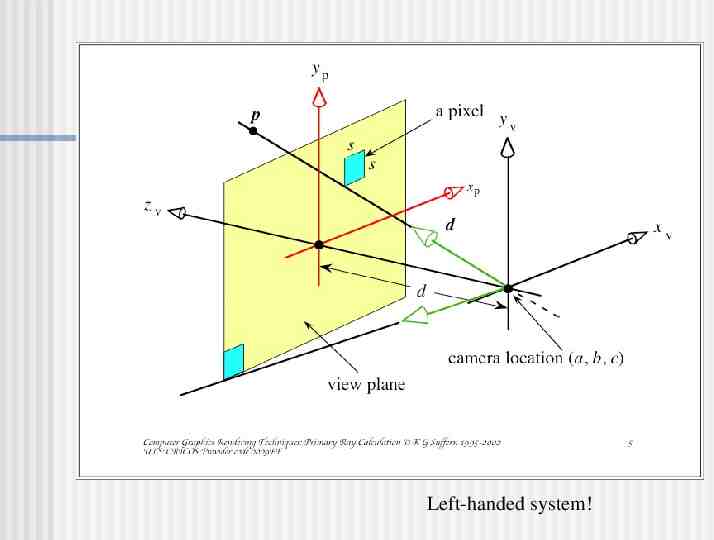
Left-handed system!
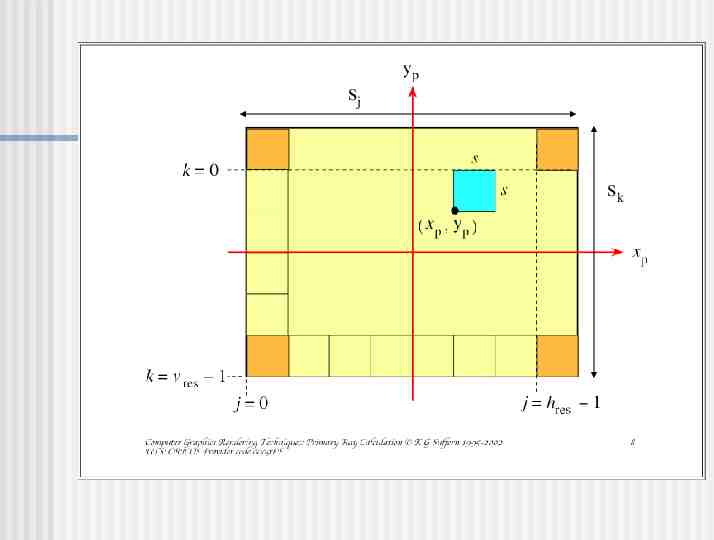
sj sk
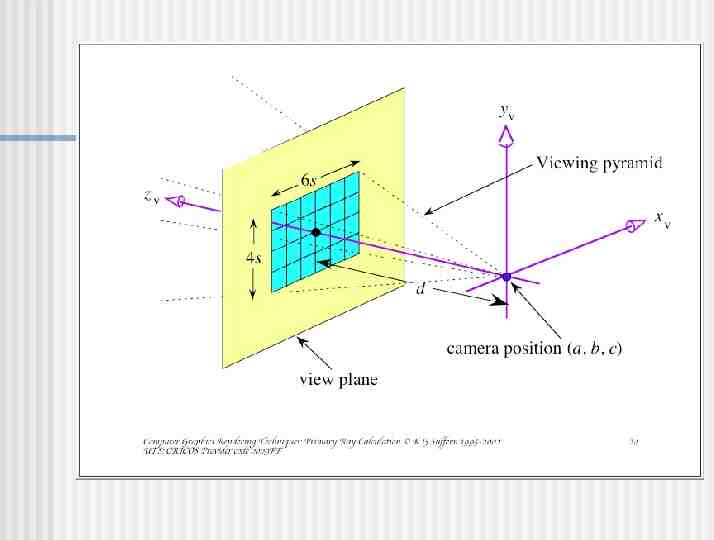
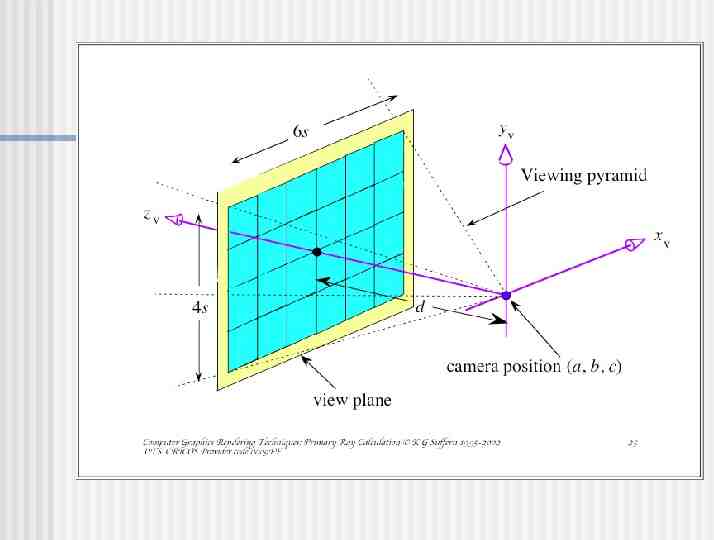
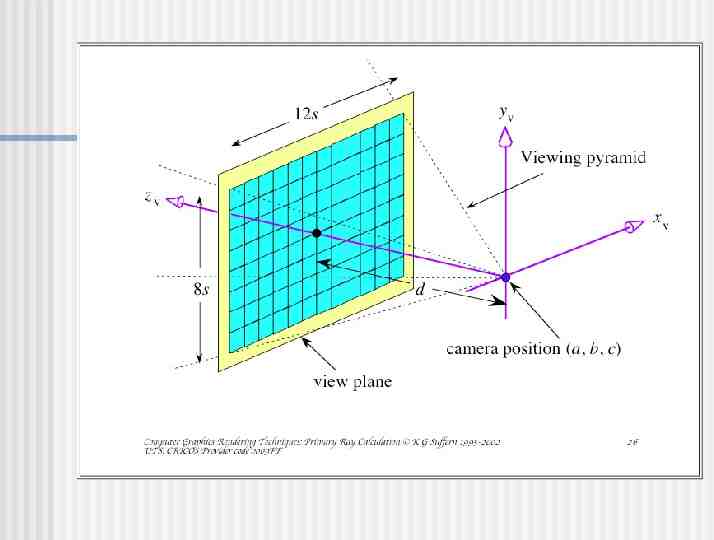
Calculating Primary Rays Given (in world coordinates) Camera (eye point) location O Camera view out direction (Zv) Camera view up vector (Yv) Distance to image plane (d) Horizontal camera view angle ( ) Pixel resolution of image plane (hres, vres) Calculate set of rays (d) that equally samples the image plane
Calculate Preliminary Values Camera view side direction (Xv) Zv Horizontal length of image plane (sj) Yv Next slide Vertical length of image plane (sk) sk sj (vres / hres) Assume square pixels
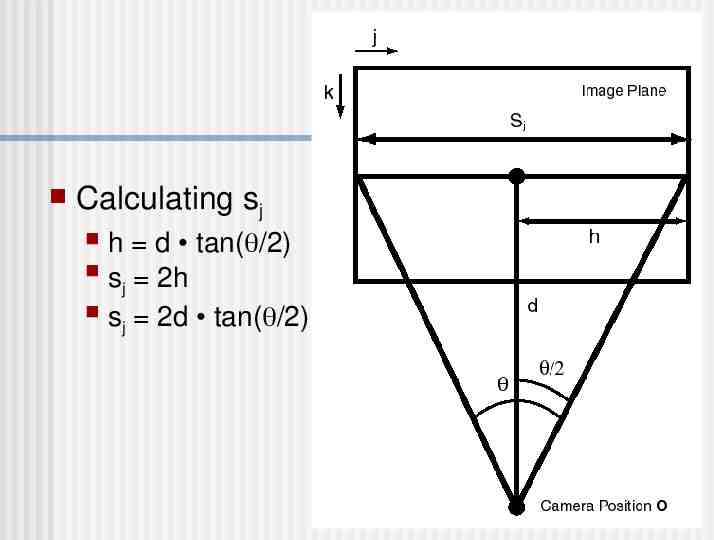
Calculating sj h d tan( /2) s 2h j s 2d tan( /2) j
Calculate Preliminary Values Position of top left pixel (P0,0) O d Zv - (Sj/2) Xv (Sk/2) Yv All in world coordinates!
Calculate Those Rays! P0,0 Xv - Yv sweeps out image plane 0 Sj; 0 Sk for (j 0; j ; j hres) for (k 0; k ; k vres) { dj,k (P0,0 Sj (j/(hres-1)) Xv - Sk (k/(vres-1)) Yv) - O; d’j,k dj,k / dj,k ; Image[j,k] ray trace(O, d’j,k , Scene); }
Parameters X and Y resolution of image Camera location & direction Distance between camera & image plane Camera view angle Distance between pixels These are not independent! Goal Choose your independent variables and calculate your d’s
I recommend setting X and Y resolution of image Camera location & orientation O & Zv & Yv Distance between camera & image plane (hres, vres) d (a positive scalar, e.g. 10) Camera view angle
Ray-Sphere Intersection G. Drew Kessler Larry Hodges Georgia Institute of Technology
Ray/Sphere Intersection (Algebraic Solution) Ray is defined by R(t) Ro Rd*t where t 0. Ro Origin of ray at (xo, yo, zo) Rd Direction of ray [xd, yd, zd] (unit vector) Sphere's surface is defined by the set of points {(xs, ys, zs)} satisfying the equation: (xs - xc)2 (ys - yc)2 (zs - zc)2 - rs2 0 Center of sphere: (xc, yc, zc) Radius of sphere: rs
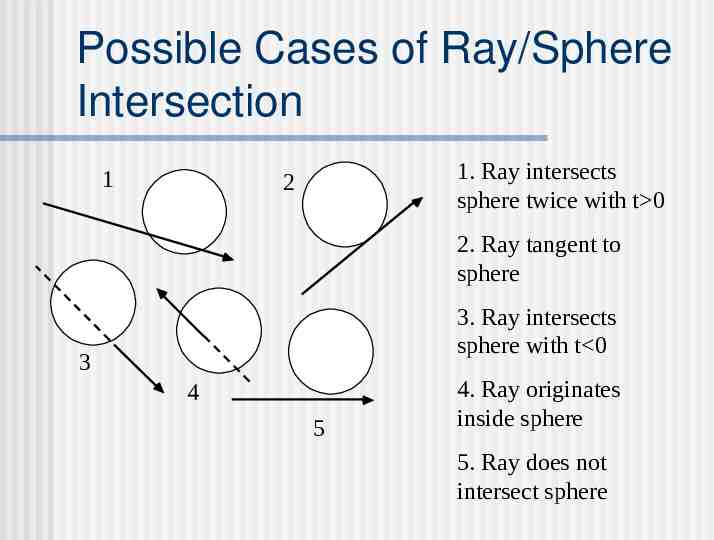
Possible Cases of Ray/Sphere Intersection 1 1. Ray intersects sphere twice with t 0 2 2. Ray tangent to sphere 3. Ray intersects sphere with t 0 3 4 5 4. Ray originates inside sphere 5. Ray does not intersect sphere
Solving For t Substitute the basic ray equation: x xo xd*t y yo yd*t z zo zd*t into the equation of the sphere: (x0 xdt - xc)2 (y0 ydt - yc)2 (z0 zdt - zc)2 - rs2 0 This is a quadratic equation in t: At2 Bt C 0, where A xd2 yd2 zd2 B 2[xd(x0 - xc) yd(y0 - yc) zd(z0 - zc)] C (x0 - xc)2 (y0 - yc)2 (z0 - zc)2 - rs2 Note: A 1
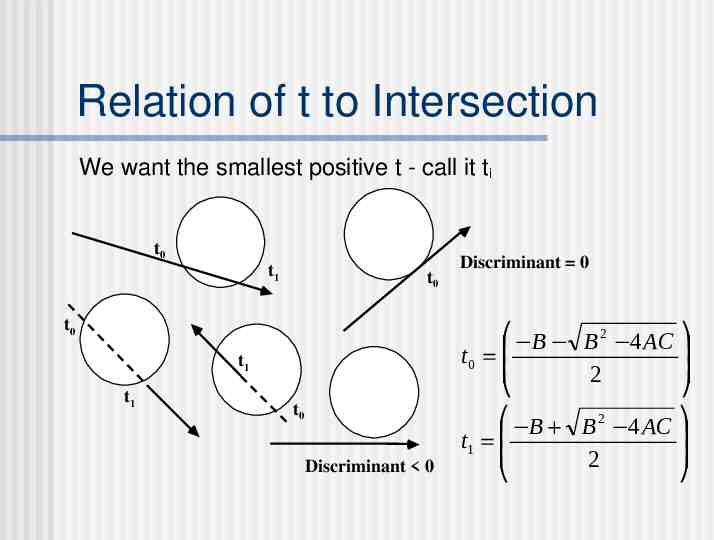
Relation of t to Intersection We want the smallest positive t - call it ti t0 t1 t0 t0 t1 t1 t0 Discriminant 0 Discriminant 0 B t0 B t1 B 2 4 AC 2 B 2 4 AC 2
Actual Intersection Intersection point, (xi, yi, zi) (xo xd*ti, yo yd*ti, zo zd*ti) Unit vector normal to the surface at this point is N [(xi - xc) / rs, (yi - yc) / rs, (zi - zc) / rs] If the ray originates inside the sphere, N should be negated so that it points back toward the center. N N
Summary (Algebraic Solution) 1. 2. 3. 4. 5. 6. Calculate A, B and C of the quadratic intersection equation Calculate discriminant (If 0, then no intersection) Calculate t0 If t0 0, then calculate t1 (If t1 0, no intersection point on ray) Calculate intersection point Calculate normal vector at point Helpful pointers: Precompute rs2 Precompute 1/rs If computed t is very small then, due to rounding error, you may not have a valid intersection
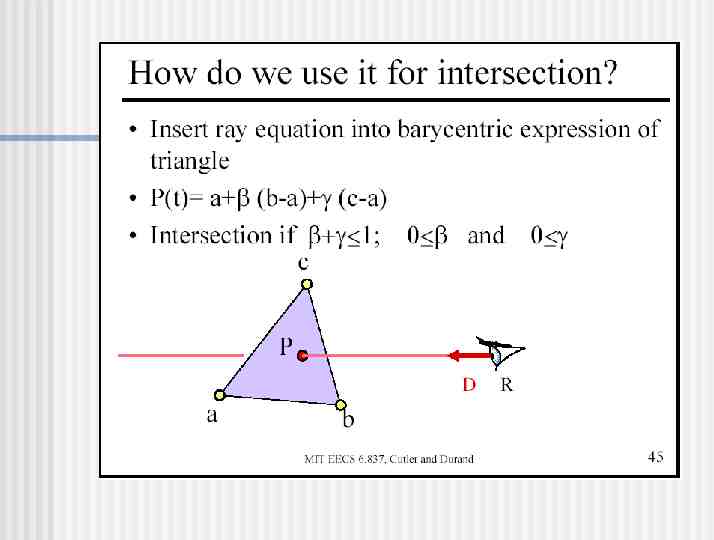
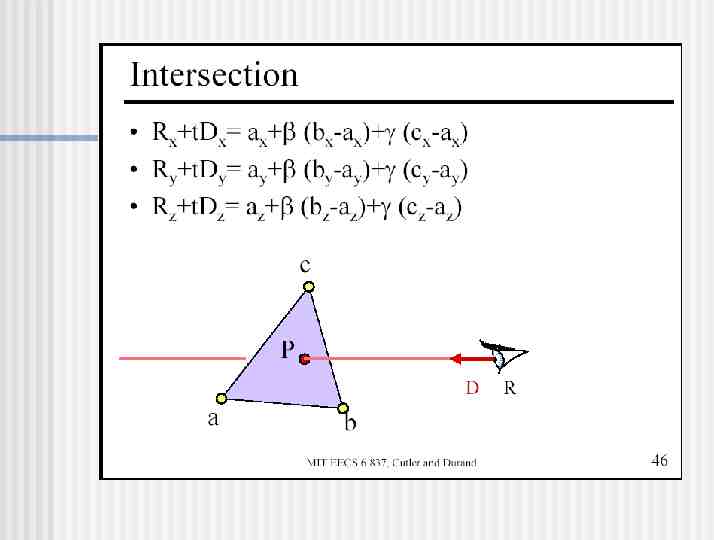
Ray-Triangle Intersection Fredo Durand Barb Cutler MIT
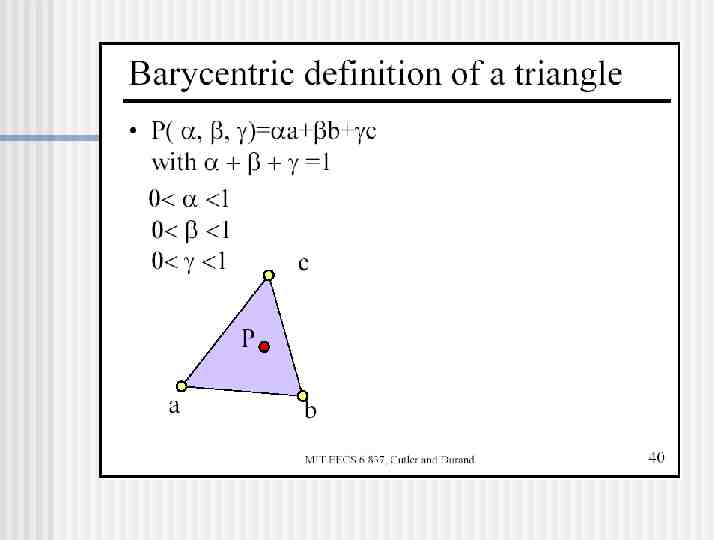
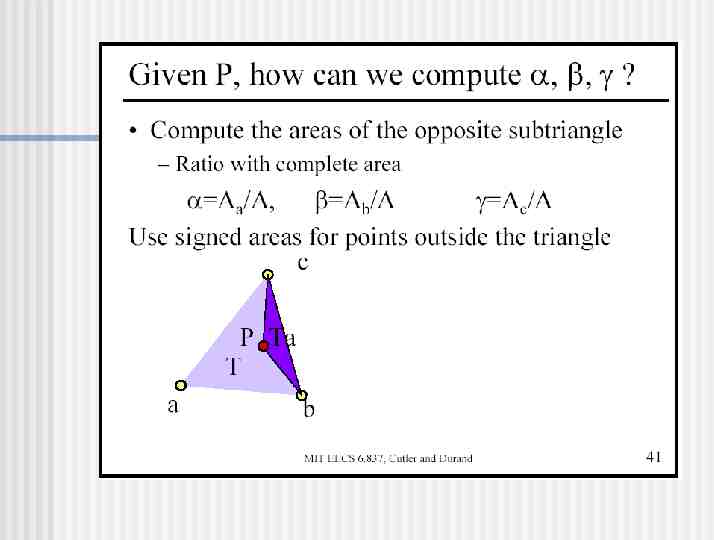
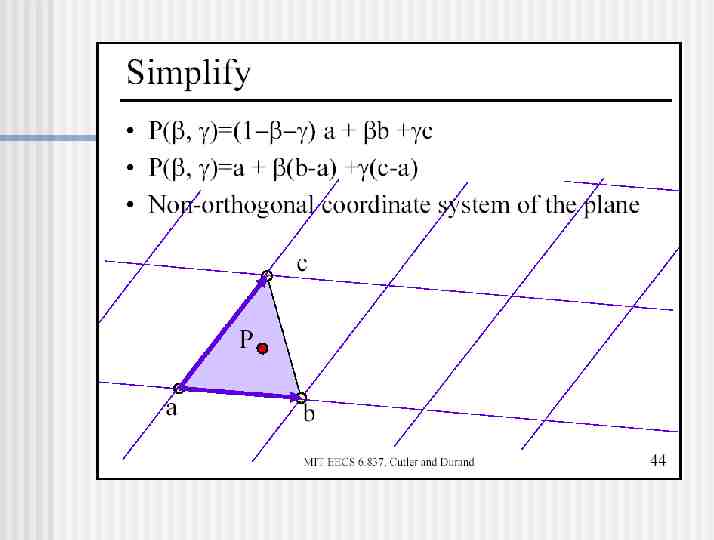
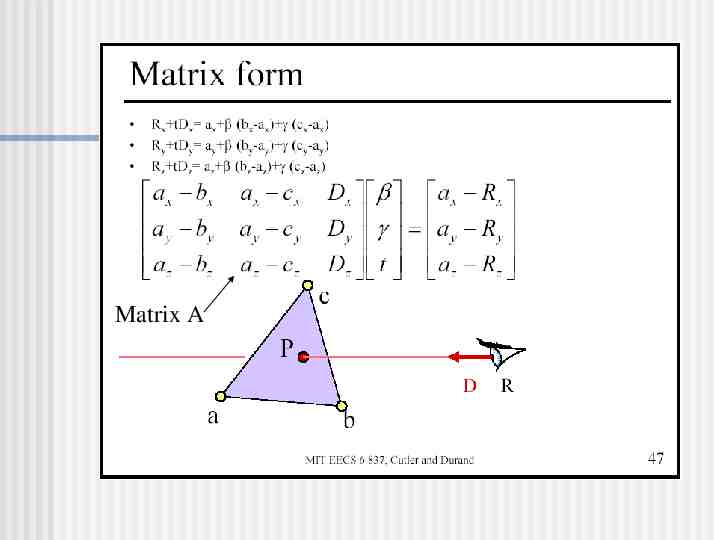
Matrix A
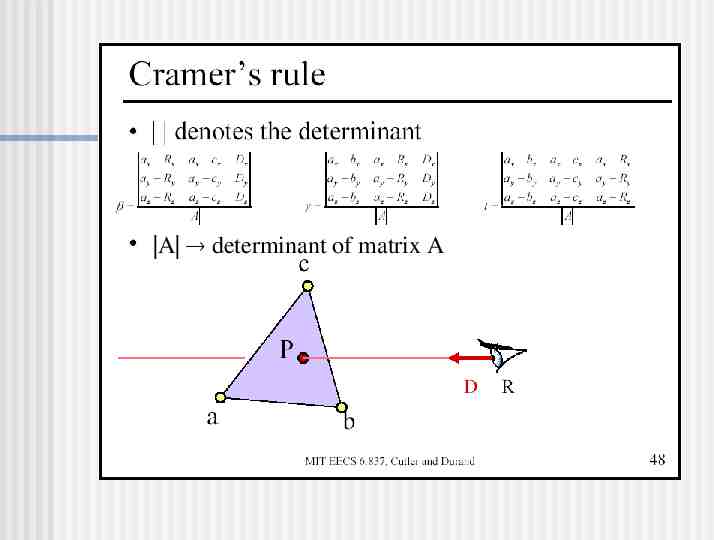
A determinant of matrix A
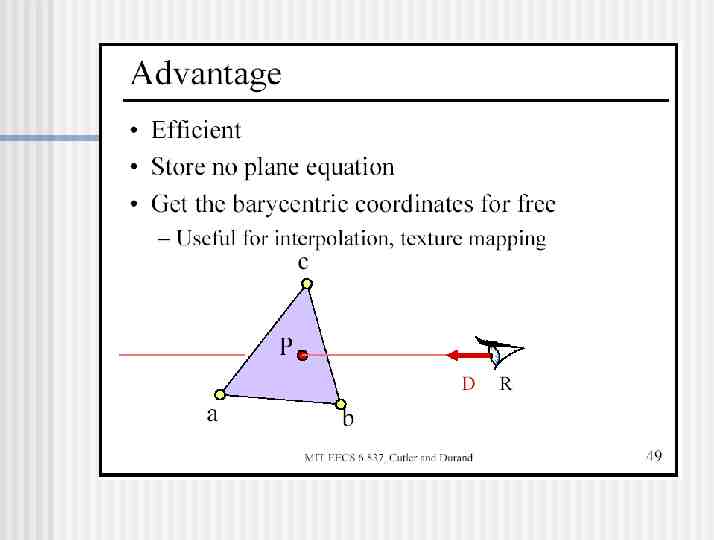
Calculate Intersection Point Are and both non-negative? Is 1? Is t non-negative? If so, you’ve got an intersection! P R tD
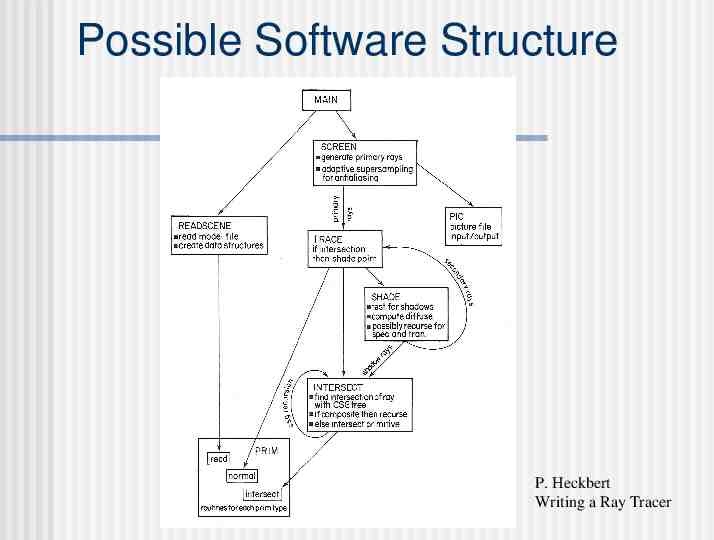
Design Your Ray Tracer! “Novice programmers often neglect the design phase, instead diving into coding without giving thought to the evolution of a piece of software over time. The result is a haphazard, poorly modularized code which is difficult to maintain and modify. A few minutes of planning shortterm and long-term goals at the beginning is time well spent.” Paul Heckbert, “Writing a Ray Tracer” Read this chapter!
Modular Functionality Read and write image files Create hierarchical geometric models with transformations Support several geometric primitives Geometric calculations & parameters Intersect arbitrary ray with scene Ray-object intersections Normals Bounding boxes Color & surface properties Texture maps Stop at first intersection (shadow rays) Recursive generation and summation of rays Adaptive sampling of image plane Light properties
Possible Software Structure P. Heckbert Writing a Ray Tracer
Progression of Assignments Basic ray tracer with spheres and triangles Triangle/sphere intersection. No shading. Simple shading and point light sources Acceleration techniques Adaptive super-sampling/anti-aliasing Shadows and reflections Transparency and refraction 2D/3D texture mapping
Wrap Up First programming assignment Due 4/13/09 Go to web page Grad students will present papers during Week 5. Need to pick paper.